三載具AS/RS作業調度優化

王 婷，王潔慈

（陜西國際商貿學院，陜西 西安 712046）

0 引言

傳統堆垛機只有一個貨位，每次進出最多只能裝載一個貨物，這不僅極大的浪費了存取調度時間，而且加速了設備的損耗。隨著社會需求的不斷發展，這種一進一出的工作方式已不能滿足企業倉儲和配送的需求。為解決上述問題，提出一種新型的倉庫，即多載具自動化立體倉庫（multi-shuttle-automated Storage and Retrieval System）。三載具堆垛機作為多載具自動化立體倉庫中常見的一種設備形式，一個子行程可以完成最多三個存貨和三個取貨任務，很好地解決了傳統堆垛機一次只能裝載一個貨物的問題，提高了存儲效率。單載具AS/RS 目前的研究成果已經不能滿足新型AS/RS運作上的要求，故而研究合理調度策略以提高三載具AS/RS作業效率刻不容緩。

現有文獻中，諸多研究仍為單載具AS/RS，卞和營，等詳細分析了堆垛機出入庫的作業方式，建立了數學模型，提出了一種基于改進遺傳算法的路徑優化方法；蔡安江，等以堆垛機執行任務所需總時間為評價標準，建立了一種基于混合命令序列的堆垛機調度模型；靳萌，等采用免疫遺傳算法求解串列立體倉庫的存取作業調度問題；李博文，等采用遺傳算法優化的集束搜索對堆垛機運行路徑進行優化，提高運行效率。Hachemi K，等以雙倍命令周期時間最小對單載具AS/RS 的存取作業進行排序處理；Chung E，等將存取調度問題處理為廣義的排序問題，并引入啟發式方法進行求解，優化效果顯著；文獻[7-9]對單載具重力式移動貨架存取調度作業進行研究，以旅行時間最小建立數學模型，并進行求解。上述文獻均在單載具存取系統作業調度中取得了良好的優化效果，但對于三載具存取系統而言，要在單載具基礎上考慮分組問題及子行程內部順序問題。

關于多載具AS/RS 的研究，文獻[10-11]和文獻[12-13]分別以雙載具和三載具AS/RS為研究對象，但主要對AS/RS的工作效率和績效性能進行評價；Yang P，等研究雙載具AS/RS進出庫復合作業，并采用一種可變鄰域搜索的方法進行求解。只考慮了單周期下的優化改進，并未對整個訂單任務進行分析研究；Drazen Popovic，等在分類存儲策略下，對三載具AS/RS的進出庫調度問題進行求解，實例結果表明了遺傳算法求解該問題的優越性；Tanaka S，等將給定貨位的多載具AS/RS作業排序問題歸納為車輛路徑（有載貨量限制）問題并對其進行探究；文獻[15-16]雖涉及多載具AS/RS存取貨作業調度問題，但是忽略了作業分組配對，只是從作業排序角度進行了探究。

針對三載具AS/RS作業調度問題，根據其工作方式，本文在研究時不再局限于單周期下的優化而是針對整批訂單，將問題轉化為分組問題、模式問題以及順序問題。且上述文獻中，堆垛機均假設為勻速運動，而堆垛機在實際運行中，具有一定的加速度，本文以更加接近實際的角度考慮堆垛機行走過程中的加速度，建立數學模型，利用混合人工蜂群算法求解模型。并采用三種算法對實例進行優化比較。在此基礎上，選用混合人工蜂群算法對單、雙、三載具堆垛機的運行效率進行計算對比。

1 問題描述

三載具AS/RS 的作業調度是指堆垛機根據訂單情況載入貨物，以適合的進出庫方式完成作業任務。由于三載具堆垛機一次可以同時載多個貨物，在考慮整個訂單存取順序的同時，也要考慮堆垛機一個子行程內的存取順序，完成合理配置，提高工作效率。

三載具AS/RS與單載具AS/RS相比，一個子行程可以完成最多三個貨物的存貨和取貨作業。在三載具AS/RS 配置下，對于一個訂單內的存取貨復合作業，首先進行指令分組，分組后每個組就是一個子行程。為了提高堆垛機工作效率，每個子行程往往采取“滿載”作業，即一個子行程可同時處理3個存貨作業和3個取貨作業，每個子行程相當于遍歷6個位置的小型TSP問題。考慮到企業的實際操作情況，在入庫時為了避免多次搬運造成的浪費，入庫順序一定，即采取先到先服務規則，而出庫貨位是由系統生成，出庫順序不定，由后續解確定最佳出庫順序。

本文研究三載具AS/RS的出入庫聯合作業，是指接收到出入庫指令后，對出入庫任務進行配對聯合、劃分任務組，使整個訂單上的任務指令都以任務組的形式呈現，每組完成3個入庫任務和3個出庫任務，每組內的完成順序需再進一步分析，直到完成所有任務組。在優化過程中，統一考慮訂單任務分組、堆垛機行走模式以及行走順序問題。

2 三載具AS/RS調度優化

傳統單載具AS/RS的復合調度作業中，堆垛機一次行程載入一個貨物同時載出一個貨物，在行程中只考慮作業配對問題，而對于三載具AS/RS作業調度的優化還需考慮指令分組、堆垛機行走模式以及子行程內部順序問題。

2.1 指令分組

指令分組是指三載具AS/RS 中對出入庫任務進行劃分任務組的過程，當出入庫任務不相等時，以補充虛擬入庫/出庫點進行調整，使得撥次中的任務都以任務組的形式呈現，然后再對任務組內的行走順序進行分析，計算行程時間。

對于三載具AS/RS而言，一個子行程要完成三個存貨和三個取貨任務，現以一個入庫任務多于出庫任務的訂單為例，入庫任務為（56，105，19，223，417，29，2，88，76，25，312，74），出庫任務為（12，542，411，30，79，300，49，66，211，315），對于該訂單任務，有多種分組方式，在不同分組下，有著不同的行程，將直接影響到整個行程時間。不同分組結果見表1。

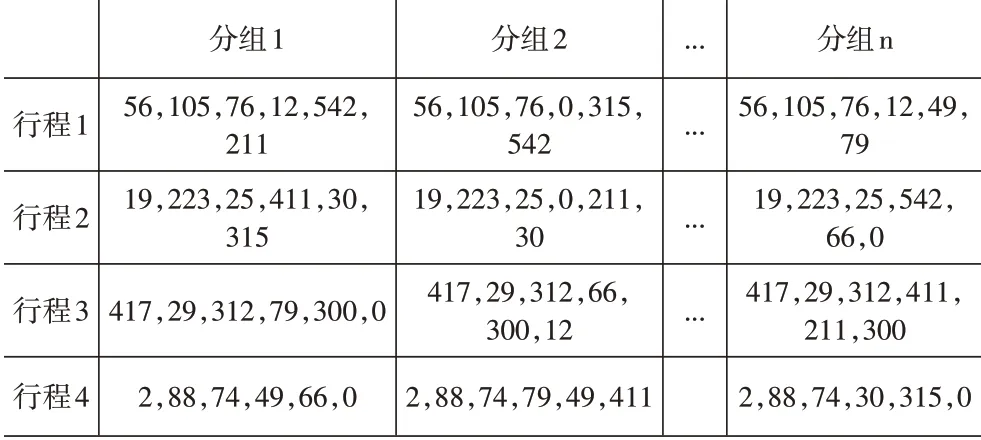
表1 分組結果表

2.2 行走模式

對于已經分組后的子行程，每個子行程對應堆垛機的一次行走過程。堆垛機按照其行走模式完成各個子行程。堆垛機“滿載”情況下，必須先存入一個貨物后才有空載位存放要取的貨物，根據載位的空、滿狀態可以得出存取貨物的關系必須滿足：存貨先于取貨，需有空載位可以存放要取的貨物。

根據實際情況，三載具AS/RS中堆垛機子行程的可行行走模式有以下五種，如圖1所示：S表示存貨作業，R表示取貨作業。L1：存→取→存→取→存→取，如圖1（a）所示；L2：存→取→存→存→取→取，如圖1（b）所示；L3：存→存→取→取→存→取，如圖1（c）所示；L4：存→存→取→存→取→取，如圖1（d）所示；L5：存→存→存→取→取→取，如圖1（e）所示。

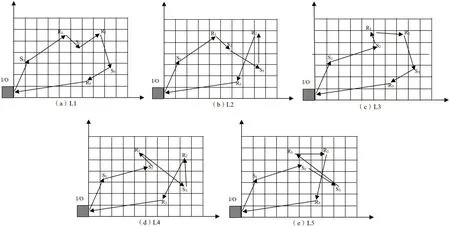
圖1 三載具堆垛機行走模式圖

2.3 行走順序

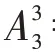
2.4 數學模型

結合以上相關問題分析，提出模型假設：（1）給定撥次內，存取貨指令已知，且對應貨位信息已知；（2）入庫順序一定，不可調換；出庫順序可以調整；（3）堆垛機為勻加速運動；（4）貨物裝載時間忽略不計。

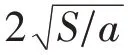
假設貨架水平方向即列方向為，垂直方向即層方向為，可得堆垛機的實際運行時間，其公式為：

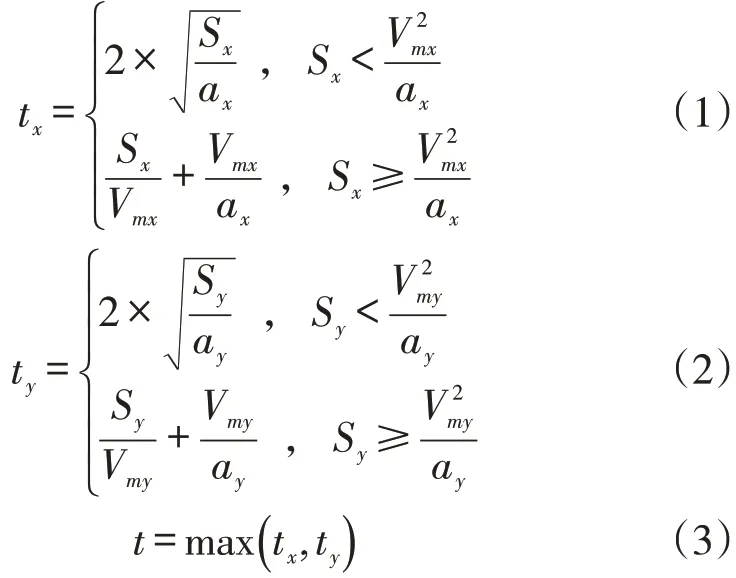
根據三載具AS/RS 的出入庫作業方式建立數學模型，需要考慮分組、模式以及順序問題。

對于每組的子行程而言，主要考慮行走模式和出庫作業順序問題，一個子行程內可以有多個可行解，不同模式下不同順序造成三載具AS/RS 的子行程內的解具有多樣化。設行走模式中出庫任務為1，2，3，取值為{123} 并且1 ≠p2 ≠p3。則對于每個子行程，貨物出入庫的時間行程時間為

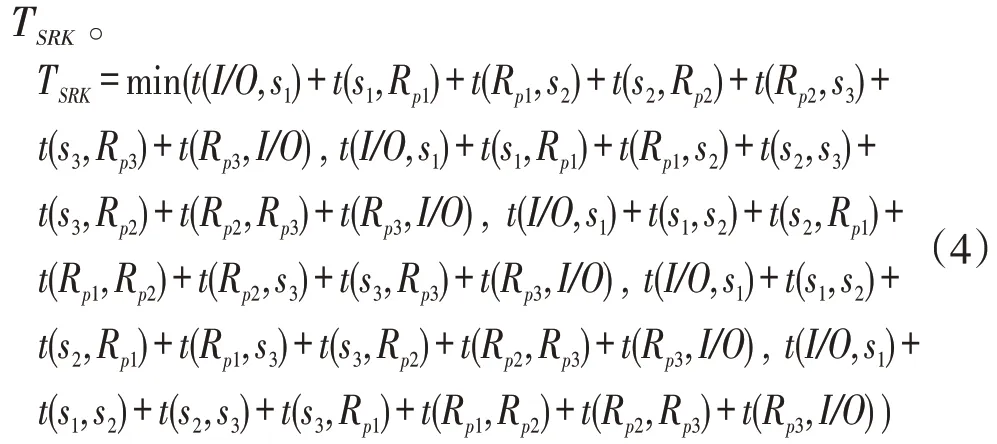
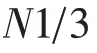
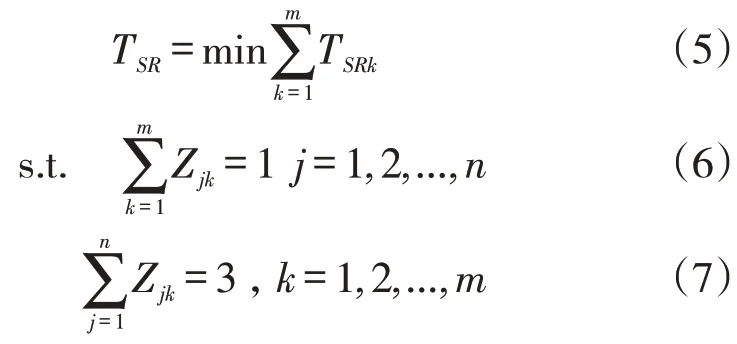
Z為決策變量，當Z=1時表示取貨指令在第個子行程中被訪問到，否則Z=0。式(6)表示每個指令對應的貨位都會被訪問；式(7)表示每個子行程執行三個取貨任務。

3 混合人工蜂群算法

人工蜂群算法(Artificial Bee Colony，ABC)是由Karaboga于2005年提出的一種新穎的基于群智能的全局優化算法，蜜蜂根據各自的分工采蜜，并交流信息，從而找到問題的最優解。

蜜蜂執行搜索活動的過程可以概括為：

（1）采蜜蜂確定蜜源，對其進行開采并記錄相關數據，尋找新密源并與觀察蜂分享數據；（2）觀察蜂在舞蹈區等待采蜜蜂分享的數據，并在臨近處選擇蜜源；（3）偵查蜂隨機找一個有意義的新蜜源。

算法流程如圖2所示。

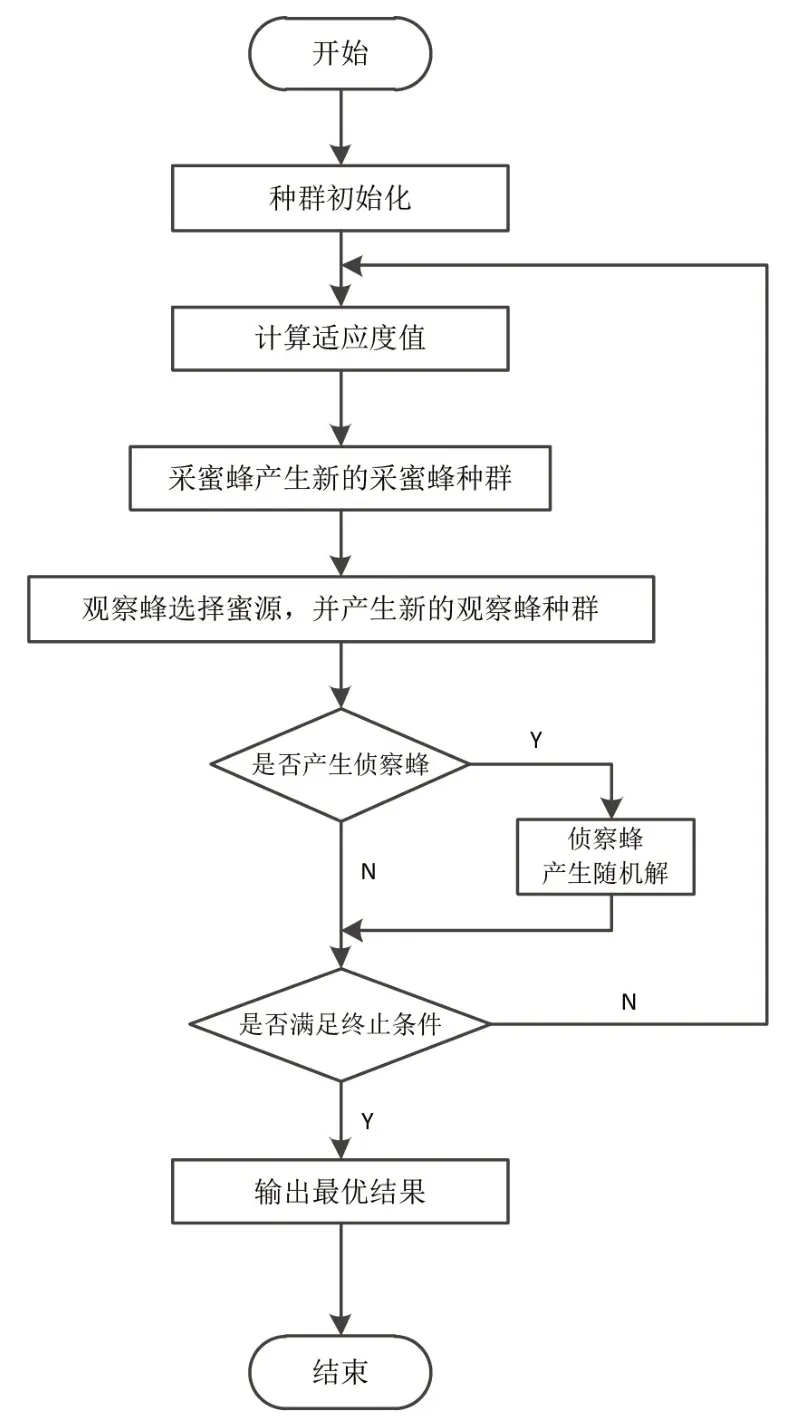
圖2 人工蜂群算法流程圖

3.1 初始化階段

初始化人工蜂群規模(2*SN)。蜜源代表了算法在搜索空間內的可行解，初始化搜索空間內的可行解依照式（8）隨機產生。

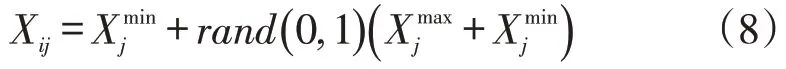
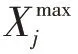
3.2 蜂群搜索階段

人工蜂群算法中采蜜蜂的搜索方程表達式為：

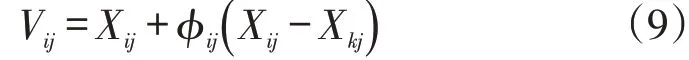
式中：V表示新蜜源；X為蜜源的第維位置，X為隨機選擇的不等于的蜜源的第維位置；?控制X領域內蜜源的出現，為[-11]內的隨機數。采蜜蜂對更新后的蜜源采用貪婪選擇策略進行選取。觀察蜂以概率值選擇蜜源，表達式為：

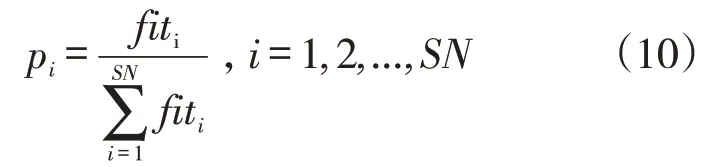
式中：為解的適應度值；為種群中解得個數。

偵察蜂在其領域范圍內搜索新蜜源，蜜源的搜索次數存在一個閥值lim it，當蜜源經過限定最大開采次數lim it 后，如果仍然沒有改進，此時采蜜蜂轉變偵察蜂，并按照式(8)進行隨機搜索產生新蜜源，新蜜源將代替該蜜源。

ABC的尋優方式傾向于不斷開發新的解，但開發效率低，為此，受到粒子群算法尋優方程的啟發，提出混合人工蜂群算法（HABC），即將粒子群算法中的粒子不斷向個體最優和全局最優粒子靠近的尋優策略代入ABC算法中，可以得出一個新的搜索方程：

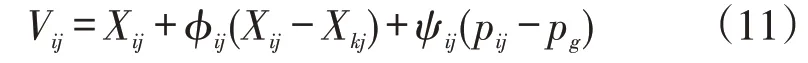
式中：ψ為[0，1.5]之間的隨機數；p為個體最優解；p為種群最優解。

個體最優解p是指個體經歷位置變化后，計算得到的適應度值最優位置，種群最優解p是指種群中的所有蜜源的適應度最優位置。蜜源每更新一次，計算一次適應度值，并且通過比較新蜜源的適應度值和個體最優值、種群最優值的適應度值更新個體最優和種群最優位置。

3.3 編碼方式、適應度函數

編碼方式：采用十進制編碼方式。

適應度函數：本文優化的目標是完成所有訂單任務的出入庫聯合作業用時最小，其計算公式為：

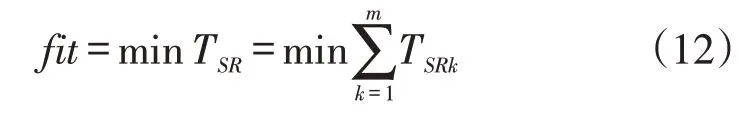
4 實例仿真

4.1 算例數據與算法參數設置

本文以某汽車零部件公司倉庫為實例分析對象，針對倉庫中某一排貨架進行實際數據統計。單排貨架為12 層，60 列，共720 個貨位。按照圖3 的方式對貨架貨位進行編碼。貨格寬度和高度尺寸為1.2m×0.8m。堆垛機水平方向最大速度v=2m/s，加速度a=0.4m/s，堆垛機垂直方向最大速度v=0.4m/s，加速度a=0.08m/s。

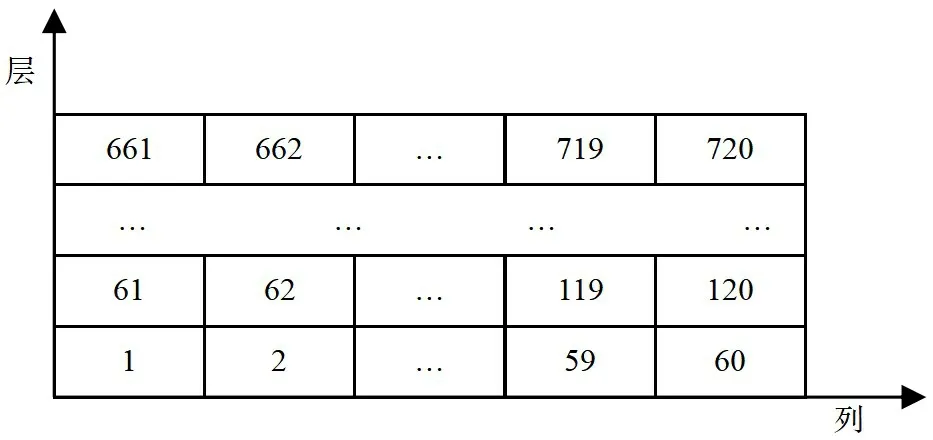
圖3 貨架貨位編號

在本文仿真實驗中，分別對出入庫任務對為30，60，90 的不同訂單進行仿真分析。以30 個出入庫任務的訂單為例，其編碼方式見表2。設置混合人工蜂群算法蜂群大小為200，其中采蜜蜂和觀察蜂各為100，蜂群食源數量即解的個數為100，最大開采次數為20；遺傳算法中取種群數n=100，變異概率Pm=0.05，交叉概率Pc=0.8。GA、ABC、HABC 算法的最大迭代次數均為6 000。

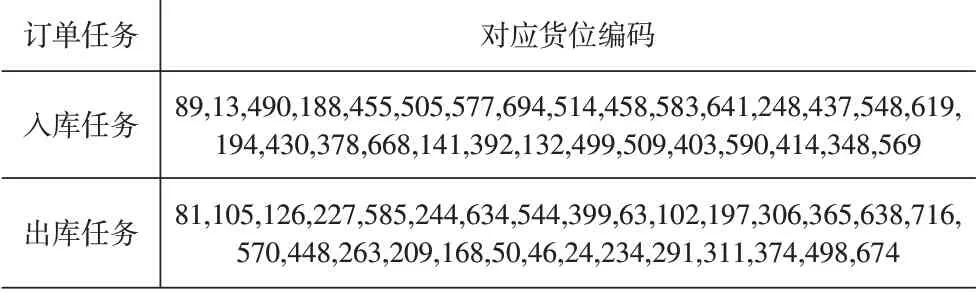
表2 出入庫任務對應貨位編碼

4.2 算法性能與仿真結果分析

為了證明所設計混合人工蜂群算法（HABC）的有效性，采用GA、ABC和HABC算法進行求解分析。為驗證所用算法的穩定性，將三種算法在30任務對、60任務對以及90 任務對等不同訂單規模下分別運行100 次，利用統計學方法求得均值和平均偏差。表3給出了不同訂單規模下的進出庫作業時間的初始解，所用算法在不同訂單規模下的進出庫作業時間最優解、優化效率、計算精度和計算效率。圖4給出了三種算法在不同訂單規模情況下的收斂圖。

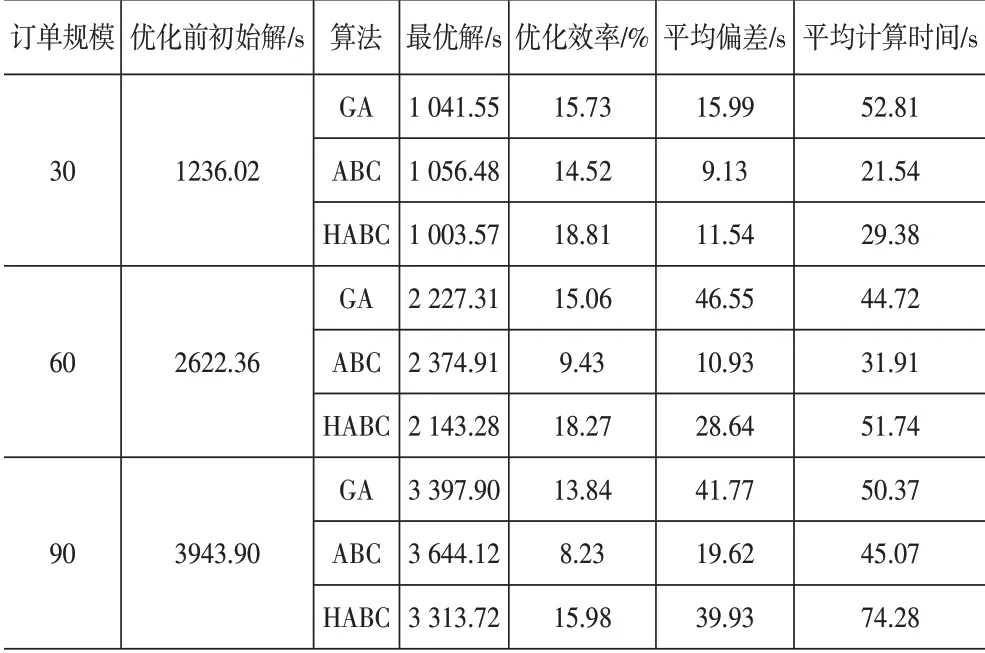
表3 三種算法在不同規模問題下的實驗結果對比

通過對表3 中三種算法的計算結果進行對比分析，得到以下結論：在不同作業規模下，HABC相較于ABC算法，雖然計算偏差較大，但是優化效率明顯提高，平均調度時間最小；相較GA求解的運算精度及優化效果都有很大程度的提高。表明本文所采用的HABC算法在解決調度優化問題上具有很好的適用性與可行性。

分析圖4中曲線可得，HABC求解得到的結果雖然收斂速度較慢，但是求解精度高，與GA對比，在迭代過程中，可以不斷的跳出局部搜索，尋找最優解。

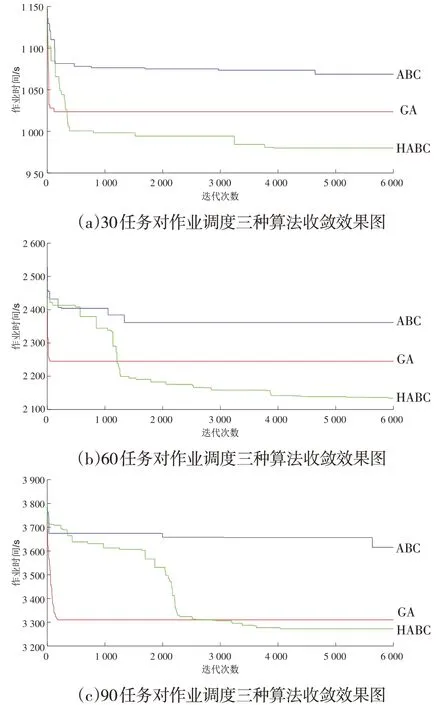
圖4 不同算法收斂效果對比圖

4.3 三載具AS/RS性能分析

本文研究對象為三載具AS/RS，為了說明其運作效率及其在工廠中更高的實用價值，利用HABC算法對單載具、雙載具AS/RS在。處理同樣訂單規模時所需時間進行計算，對比分析三載具AS/RS 的性能狀況。表4為三種訂單規模下的單、雙、三載具AS/RS的進出庫時間對比分析表。圖5為不同載具數AS/RS作業調度算法收斂圖。

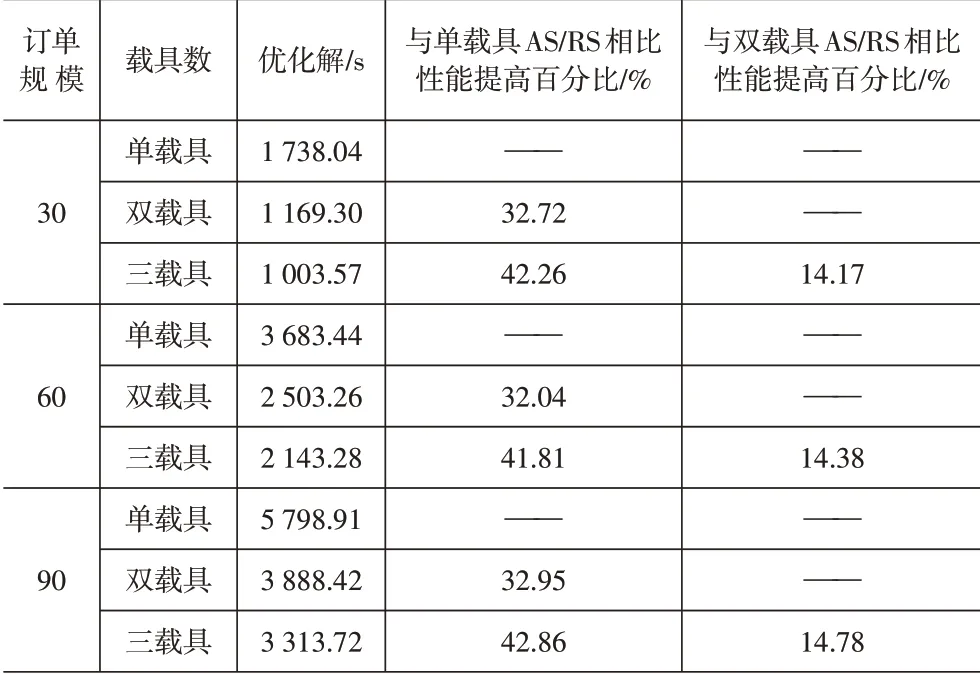
表4 不同載具數AS/RS運作效率對比表

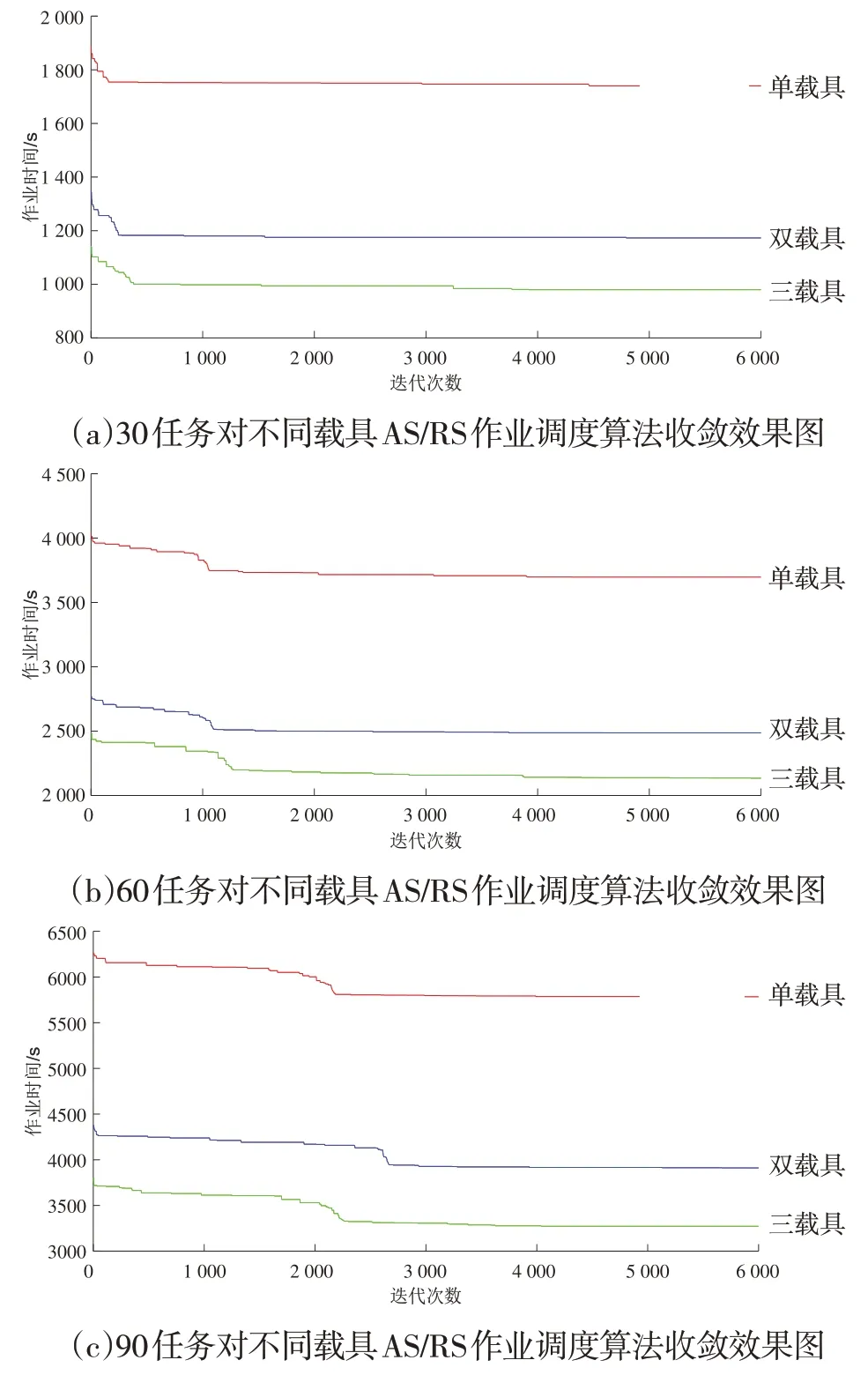
圖5 三種不同載具作業調度算法收斂圖

通過對不同載具數AS/RS的運作效率進行對比，實例結果表明，三載具AS/RS較雙載具AS/RS在同樣訂單規模下，其運作效率提升了14%左右；三載具AS/RS的運作時間遠小于單載具，效率大大提升，在同樣訂單規模下，其運作效率提升了42%左右。

5 結語

本文從分組配對、行走模式以及行走順序三個方面對三載具AS/RS的作業調度問題進行全面分析，建立了出入庫聯合作業的優化模型，并采用混合人工蜂群算法對模型進行求解，利用實例對算法性能進行分析，在30、60、90任務對的不同訂單規模下，將三種算法性能進行比較分析，結果表明：混合人工蜂群算法的優化效果最佳，優化效率分別達到18.81%、18.27%和15.98%。通過與單、雙載具AS/RS在處理同種規模訂單下的處理時間進行對比，結果表明，三載具AS/RS性能遠高于單、雙載具AS/RS，具有更高的實用價值，可以有效縮短作業時間，提升運作效率，降低企業成本。