基于模糊聚類和Slope One填充的推薦算法

李磊

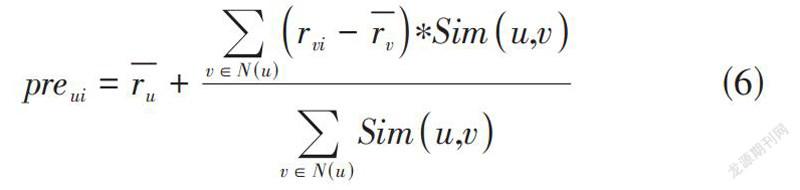
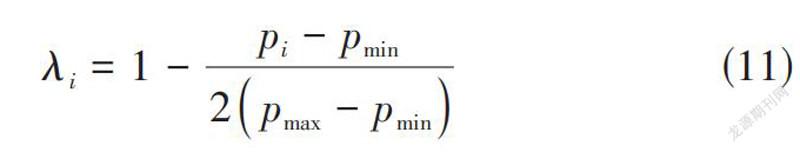
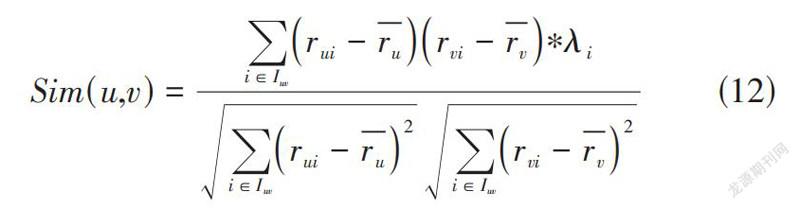
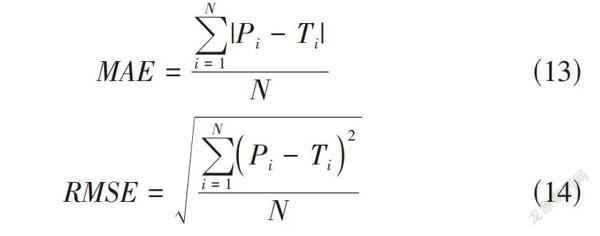
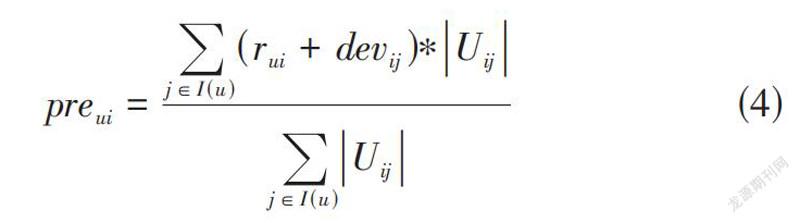
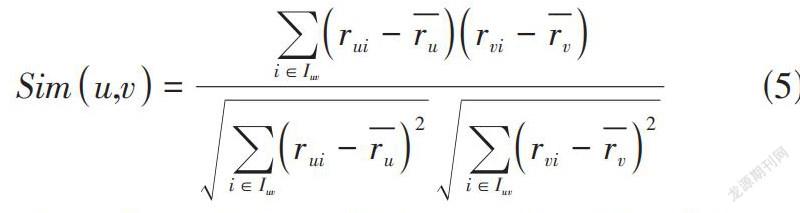
摘要：傳統的推薦算法受限于其數據密度低，矩陣規模大進而導致的計算復雜、實時性差且推薦精度低。針對這一問題，設計了一種結合模糊聚類和Slope One填充的推薦方法。算法根據用戶的特征進行模糊聚類，利用加權Slope One算法填充c個規模較小的用戶-項目矩陣中的缺失數據，并通過改進的相似度計算方法計算出用戶間的相似度得出最近鄰結果集。仿真對比實驗表明，設計的算法對比傳統的推薦算法在精度上有著很大提升，同時能緩解數據稀疏性，提升推薦質量。

關鍵詞：協同過濾;模糊聚類;Slope One;相似度

中圖分類號：TP391? ? ? 文獻標識碼：A

文章編號：1009-3044（2022）10-0068-03

1 引言

由于信息網絡的高速增長，世界各地的數據量也正瘋狂增加，據有關組織報告稱，估計到2025年，世界各地的數據量將會達到驚人的163ZB，是2016年16.1ZB的十倍[1]。面對如此龐大的數據量，我們已然陷入了“信息過載”的時代[2]。若是能夠使用一種方法能夠挖掘出用戶的歷史行為記錄并分析計算出用戶潛在的興趣，主動地推薦感興趣的項目給用戶，則大概率可避免用戶大海撈針似地獲取數據。推薦系統應運而生。

推薦系統的質量好壞完全依賴于為該系統設計的推薦算法，作為最經久不衰最為經典的一種推薦算法——協同過濾算法，為緩解大數據環境下存在的“信息過載”問題做出了巨大的貢獻。通過構建用戶-項目矩陣，通過分析用戶行為找出相似的用戶，然后根據相似用戶的行為做出推薦。但是可擴展性差、數據密度低導致稀疏性高從始至終都是亟須解決的問題。究其原因是用戶和項目之間的不對稱性，導致大量的項目僅僅被極少比例的用戶所標注[3]。

為了緩解由于數據密度低，矩陣規模龐大進而導致推薦精度不高、可擴展性差這一系列問題。論文設計了一種基于模糊聚類和Slope One填充的推薦算法。首先使用模糊c均值算法（FCM）按照用戶的特征進行聚類，得到c個聚類中心進而構建c個用戶項目矩陣，然后使用加權Slope One算法計算出的結果值回填矩陣中的缺失項，最后和協同過濾算法相融合得出預測評分。實驗表明，論文和設計出的算法在各項指標中均優于傳統的推薦算法。

2 相關研究

2.1 協同過濾算法

GlodBerg等人[4]在20世紀90年代開創性地提出了協同過濾算法。其基本假設是，“物理類聚，人以群分”。協同過濾技術主要包含以下三個步驟：

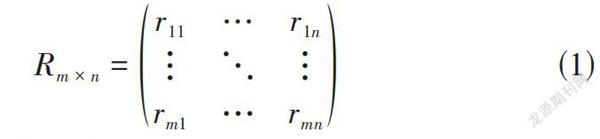
1） 建立用戶-項目矩陣。通過日志或其他方式對用戶的操作行為，包括顯示反饋或是隱式反饋進行收集，得到用戶-項目評分矩陣[Rm×n]如公式（1）所示。

[Rm×n=r11…r1n???rm1…rmn]? ? ? ? ? ? ?（1）

2） 找到用戶最近鄰集合。描述兩個樣本特征的相似程度需要使用到相似性計算方法。構建相似度矩陣隨后從中提取出與目標樣本相似程度最高的前k個樣本作為最近鄰集合。

3） 產生推薦。通過近鄰結果集合加權得出預測評分結果進而產生排序Top-N推薦列表給用戶進行推薦。

2.2 Slope One算法

Slope One算法[5]其核心思想是利用一種線性回歸模型來對矩陣中存在的缺失值進行預測。使用公式（2） 計算得出各個項目評分差均值[devij]，然后使用公式（3） 進行目標用戶對其項目的評分預測。

[devij=u∈N（i）?N（j）rui-rujN（i）?N（j）]? ? ? ? ? ? ? ? ? （2）

[pui=i∈N（u）|N（i）?N（j）|?ruj+deviji∈N（u）N（i）?N（j）]? ? ? ? ? ? ?（3）

[rui]代表的是項目i被用戶u所標注并給出了評分， [N（i）?N（j）] 代表的是針對項目i和j均存在共同標注行為的用戶集合。

2.3 Weighted Slope One算法

Slope One算法簡單高效可擴展性強。但是未考慮共同評分個數多的要比共同評分個數少的更加可靠，因此在進行評分預測階段時應當賦予更高的權重比例[6]。加權Slope One算法如公式（4） 所示：

[preui=j∈I（u）（rui+devij）?Uijj∈I（u）Uij]? ? ? ? ? ? ? （4）

2.4 相似性計算方法

相似度計算是產生推薦的重要步驟之一，論文選取皮爾遜相關系數作為衡量相似與否的標準，如公式（5） 所示。

[Simu，v=i∈Iuvrui-rurvi-rvi∈Iuvrui-ru2i∈Iuvrvi-rv2]? ? ? （5）

其中，[Simu，v]的含義是兩個樣本u和v之間的相似度， [ru]和[rv]分別表示為各自對它們有過評分行為的項目的平均評分值。

2.5 評分生成

通過相似鄰居集合以及其評分信息聯合計算得出最終的預測評分，如公式（6） 所示：

[preui=ru+v∈N（u）rvi-rv?Simu，vv∈N（u）Simu，v]? ? ? ? ? ? ?（6）

[preui]表示的是用戶u對項目i計算得出的預測評分值， [N（u）]含義為對目標用戶u所挑選出的最近鄰用戶集。

3 本文算法

3.1 用戶模糊聚類

在傳統的聚類算法中，每個目標樣本都只能被劃分都一個固定的類別中去，沒有達到一種靈活的狀態。模糊聚類通過引入隸屬度這一特性提供了更有彈性更加靈活的聚類效果[7]，根據隸屬度的權重將一個目標樣本劃分到不同的類簇中去。其中最被廣泛應用的是模糊c-均值聚類（FCM）算法[8]。

在FCM算法中，將用戶特征屬性映射到n維向量u上，[u=r1，r2，…rn]，將數據集[X=x1，x2，…， xn]中各個樣本點根據自身的特征屬性按照相應的隸屬度模糊劃分到不同的聚類簇中心，不斷迭代前后兩次的目標函數之差直到比最初設置的最小值小或是已經達到了最大的系統設置的迭代次數則終止，此時即可獲得相對最佳的聚類效果[9]。原問題可以看作求解拉格朗日條件極值問題，其目標損失函數為公式（7） 所示，其約束條件為從各個樣本點出發最終到達所有的聚類中心必須滿足隸屬度權重總和為1，如公式（8） 所示。

[J（U，ci）=i=1cj=1nuixjmxj-ci]? ? ? ? ? ? ? ? ? ?（7）

[i=1cuixj=1，?j=1，2，…，n]? ? ? ? ? ? ? ? ? ?（8）

[uixj]表示的含義是對于樣本集中的某個樣本[xj]其隸屬于第i個聚類中心的程度，m為加權指數，通常取2時效果最好。[xj-ci]代表的是樣本點[xj]到某一個固定的聚類中心[ci]之間第二范數，也被稱作歐幾里得距離。為了使得目標損失函數（7） 能夠取得極小值，需要構造并求解拉格朗日函數，對[ci]與[uixj]求偏導數即可得到相應的必要條件使得原目標函數能夠取得極小值，如公式（9） 、公式（10） 所示。

[ci=j=1nuixjmxjj=1nuixjm]? ? ? ? ? ? ? ? ?（9）

[uixj=i=1kxj-cixj-ck2m-1-1]? ? ? ? ? ? ? （10）

FCM聚類算法步驟流程如下所示：

輸入：數據集樣本和聚類個數c;

輸出：使得公式（7） 取得極小值的聚類中心集合[ci]。

Step1：指定聚類個數c，初始化加權指數m;

Step2：使用隨機函數生成各個聚類中心;

Step3：求解出每個樣本點到達各個聚類簇中心的隸屬度，并構建出相應的隸屬度矩陣;

Step4：計算迭代得出各個簇的聚類中心;

Step5：不斷迭代前后兩次的目標函數之差直到比最初設置的最小值小或是已經達到了最大的迭代次數則終止，否則返回Step3;

Step6：得到聚類中心集合[ci]。

3.2 改進的相似度計算方法

針對大多數行業中，如電商、影視等，越是熱門的項目越容易被曝光使得更多的人購買或觀看，相比之下，越是曝光度不高的項目越難被用戶所發現。這種現象也被稱作“馬太效應”。所以引入項目流行度因子[λ]以此來降低熱門商品的所占的權重。

[λi=1-pi-pmin2pmax-pmin]? ? ? ? ? ? ? ? ? ? ?（11）

[pi]代表項目i的流行度，反映出的是項目i被標注過的次數，[pmax]是所有項目中最大標注數目，[pmin]為最小標注數目。[λi]的取值范圍為[0，1]區間上。則改進后的相似度計算方法為：

[Sim（u，v）=i∈Iuvrui-rurvi-rv?λii∈Iuvrui-ru2i∈Iuvrvi-rv2]? ? （12）

3.3 基于模糊聚類和Slope One填充的推薦算法

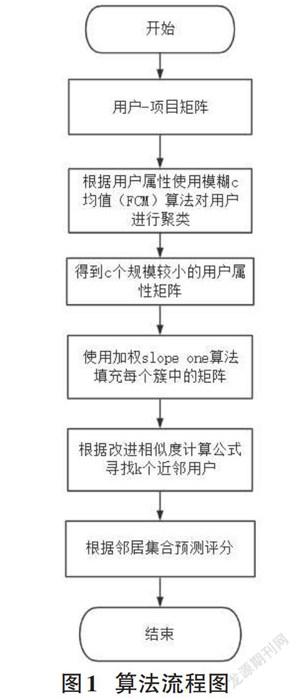
為了緩解協同過濾算法中一直以來存在的數據密度低致使在相似度計算時，未能抓到最相似的近鄰集合進而導致推薦精度不高的問題，論文使用模糊聚類方法根據用戶特征進行聚類，也即等價于對原始的用戶-項目矩陣進行降維，降維后可得到c（c為聚類個數） 個小規模的矩陣。利用加權Slope One算法為每個矩陣進行屬性填充，根據聚類的特性這就會使得在同一個聚類簇下的用戶相似程度顯然比非同一簇下的相似度要高。所以Slope One算法在填充矩陣時會盡可能避免到不相似用戶的干擾，從而可以提升推薦的精度，論文的算法流程圖如圖1。

算法執行步驟如下：

輸入：數據集，聚類數c，最近鄰數量k;

輸出：待預測用戶對某個項目的最終評分預測值。

Step1：加載數據集，構建用戶-評分矩陣D，使用公式（7） 、公式（8） 、公式（9） 、公式（10） 根據用戶屬性特征進行聚類，形成c個聚類簇，并構建c個規模較小的用戶-項目評分矩陣;

Step2：在這些小規模的用戶-項目矩陣當中，使用公式（2）得出[devij];

Step3：在得到[devij]的基礎上通過公式（4）計算出[preui];

Step4：[preui]的值回填矩陣中空缺的數據，得到c個新的規模較小且稠密用戶-項目評分矩陣[Dβ];

Step5：在稠密的矩陣[Dβ]上使用公式（12） 構建出相似度矩陣，挑選出最相近的k個用戶;

Step6：在測試集中根據上一步驟得出選出目標用戶的最近鄰集合，借此來預測目標用戶對某個項目的評分;

Step7：通過公式（6） 得到最終的評分預測結果。

4 實驗結果分析

4.1 實驗數據

實驗選取由GroupLens研究小組發布的電影評分MovieLens數據集。這是個性化推薦算法中最為經典的數據集，選取ml-100k來驗證論文算法。數據集的評分范圍為1～5中的整數，評分的高低代表著用戶的喜歡或是不喜歡程度。

4.2 評測指標

論文選取平均絕對誤差（Mean Absolute Error，MAE） 、均方根誤差（Root Mean Square Error，RMSE）作為實驗的評測指標。MAE和RMSE是在推薦系統中流傳最為經典、使用頻率最高的評估指標，得出的結果越小則可以充分反映出算法的誤差小準確率高。

[MAE=i=1N|Pi-Ti|N]? ? ? ? ? （13）

[RMSE=i=1NPi-Ti2N]? ? ? ? ? ? ? ? ? ?（14）

其中[Pi]是論文提出算法得出的預測評分，[Ti]是樣本真實打分，N是在測試集中待預測樣本的總數。

4.3 實驗設計與結果分析

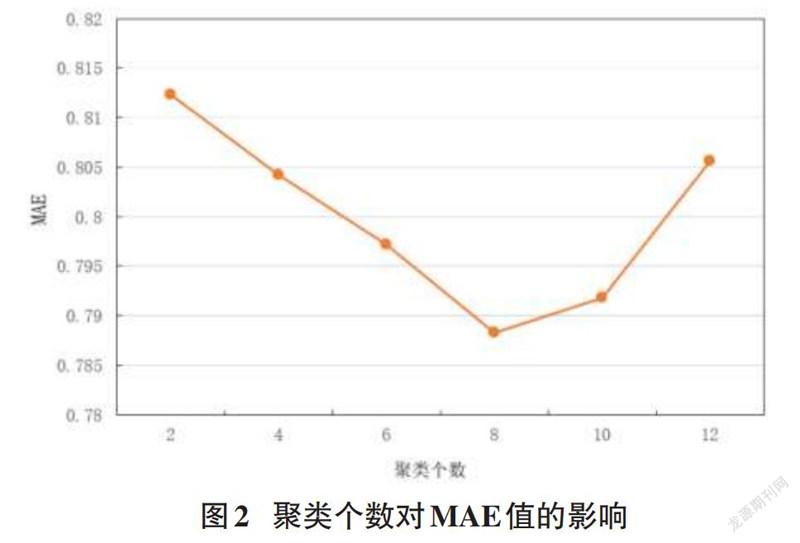
實驗一：驗證聚類個數對算法實驗結果的影響并根據實驗結果挑選取最佳聚類個數。

設定聚類個數為[2，12]，每組的間隔為2進行了多組實驗，從圖中能夠明顯看出當聚類個數達到8時，誤差最小效果最好。

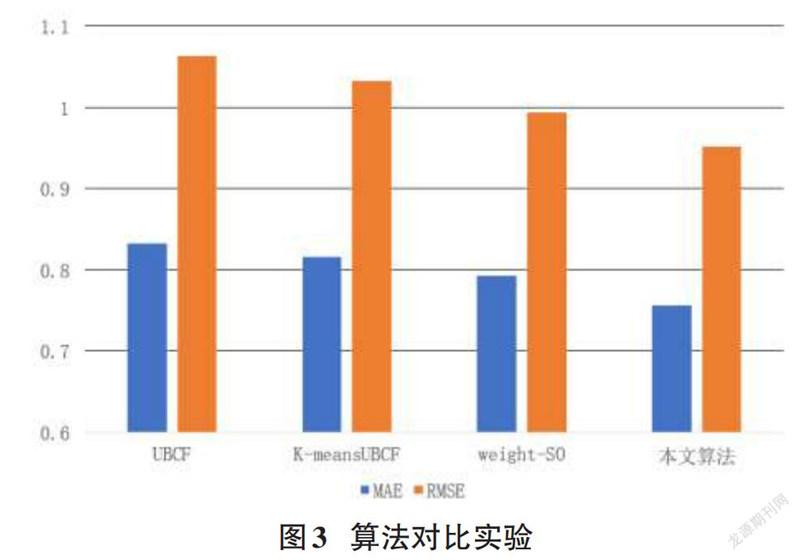
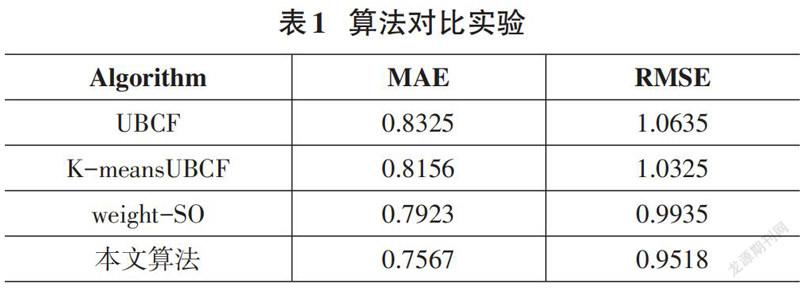
實驗二：對比傳統的基于用戶的協同過濾算法（UBCF） 、基于加權Slope One算法（weight-SO） 、基于k-means聚類的協同過濾算法。論文選取近鄰個數為60，聚類簇數為8，實驗結果如圖3和表1所示：

從圖表中能夠清晰地看到，論文設計的算法的誤差均小于其余算法，MAE值對比UBCF、K-meansUBCF、weight-SO算法分別降低了大約有7.58%、5.89%、3.56%，RMSE值降低了大約11.17%、8.07%、4.17%。相比于UBCF算法由于其數據密度低稀疏性高導致近鄰選擇不準確影響了推薦結果。相比于WSO算法，由于其未考慮用戶之間的相似度，是在全局范圍內進行預測填充，影響了其推薦的精度。論文提出的算法不僅考慮到

了項目的流行性，優化了相似度的計算方法，而且考慮到數據稀疏性帶來的負面影響，從而提升了推薦精度。

5 結束語

數據稀疏，可擴展性一直以來都是傳統推薦算法面臨的問題，針對問題出發，在深入理解模糊聚類和Slope One算法理論模型的基礎上，設計了基于模糊聚類和Slope One填充的推薦算法，根據實驗結果可以分析出設計的算法能夠緩解由于數據密度低，稀疏性高導致的推薦精度較低的問題，由于聚類都是離線完成的，在進行評分預測時不需要遍歷整個用戶-評分矩陣，只需在屬于的簇中計算相似度即可，減少了計算時間，可擴展性強。 在以后進一步研究當中將會考慮引入更多的輔助信息，如用戶偏好、興趣度、信任度、長短期興趣等模型并融入算法中并針對FCM算法其目標函數是一種非凸函數導致其難以取得全局的最優解 ，考慮引入智能優化方法進一步提升推薦質量。

參考文獻：

[1] 李悅，謝珺，侯文麗，等.融合用戶偏好優化聚類的協同過濾推薦算法[J].鄭州大學學報（理學版），2020，52（2）：29-35.

[2] 王巖，張杰，許合利.結合用戶興趣和改進的協同過濾推薦算法[J].小型微型計算機系統，2020，41（8）：1665-1669.

[3] 張艷菊，陸暢.數據缺失下的IFCM-Slope One協同過濾推薦算法[J].統計與決策，2020，36（9）：185-188.

[4] Goldberg D，Nichols D，Oki B M，et al.Using collaborative filtering to weave an information tapestry[J].Communications of the ACM，1992，35（12）：61-70.

[5] Lemire D，Maclachlan A.Slope one predictors for online rating based collaborative filtering[C]∥Proceedings of the 2005 SIAM Data Mining Conference，2005：471-480.

[6] 馬浩，黃俊，孔麟，等.動態k近鄰輔助多權值Slope One算法[J].計算機工程與設計，2020，41（11）：3072-3077.

[7] Manochandar S，Punniyamoorthy M.A new user similarity measure in a new prediction model for collaborative filtering[J].Applied Intelligence，2021，51（1）：586-615.

[8] 賈俊杰，張玉超.基于用戶模糊聚類的綜合信任推薦算法[J].計算機工程，2021，47（6）：60-67.

[9] 李建軍，付佳，楊玉，等.基于混沌粒子群聚類優化的協同過濾推薦[J].計算機工程與設計，2021，42（8）：2173-2179.

【通聯編輯：謝媛媛】