引信殉爆閾值數值模擬

王 慧

（海軍裝備部裝備審價中心，北京 100071）

當炸藥發生爆炸時，爆炸所產生的爆轟波和爆炸碎片導致間隔一定距離的另一個炸藥發生爆炸的現象，稱為殉爆[1]。袁俊明等對裸裝聚奧-9C（JO-9C）傳爆藥進行了引信殉爆數值模擬，分析了殉爆過程中JO-9C爆轟波的成長歷程和傳播規律[2]。KIM等利用流體動力學模型，分析了PBXN-9炸藥一對多殉爆的影響因素[3-4]。陳朗等計算了不同距離下裸裝固黑鋁（GHL）炸藥的殉爆距離，分析了炸藥殉爆過程中被發炸藥中爆轟波的成長歷程[5-7]。文中通過沖擊波作用傳爆序列殉爆數值模擬，考慮導爆管的作用，獲得了引信傳爆管的殉爆距離和安全距離。

1 有限元模型

1.1 材料模型

利用Jones-Wilkins-Lee（JWL）描述起爆藥的反應狀態pe和未反應狀態pg分別為：

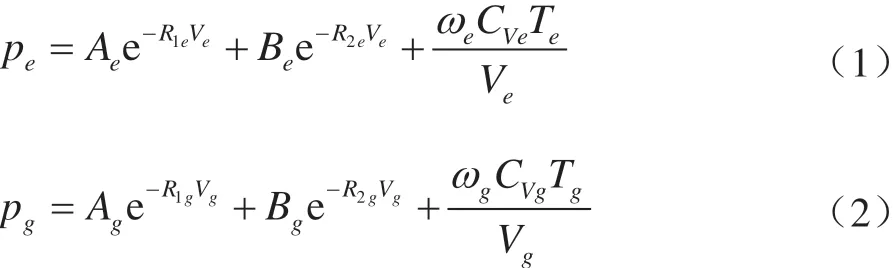
式中：p為壓強；V為相對比容；T為溫度；A、B、R1、R2、ω和Cv為常數；下標e和g分別表示反應炸藥和反應產物。

反應速率方程：

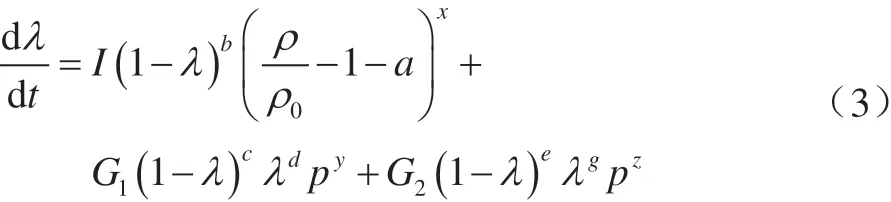
式中：λ為炸藥反應度；t為時間；ρ為密度；p為 反 應 壓 強；I、G1、G2、a、b、x、c、d、y、e、g和z為12個可調的擬合系數。

1.2 數值模型與方法

采用非線性有限元軟件LS-DYNA 3D對引信傳爆序列進行殉爆數值模擬。起爆點設置于起爆藥上端中心點處，考慮爆炸沖擊波對引信傳爆序列的沖擊作用，引信傳爆序列結構如圖1所示。傳爆序列中，JH-14C的尺寸為38.0 mm 15.5 mm，并使用True Grid建立1/2三維有限元模型。

1.3 材料參數

各材料參數如表1和表2所示。導爆藥、傳爆藥和起爆藥分別為RDX-8701[8]、JH-14C和Comp B炸藥。表1中，C、S1、γ0分別為格呂奈森方程截距、斜率和系數。表2中，Cp、G、SIGY分別為聚氨酯本構模型中的系數、剪切模量和屈服模量。

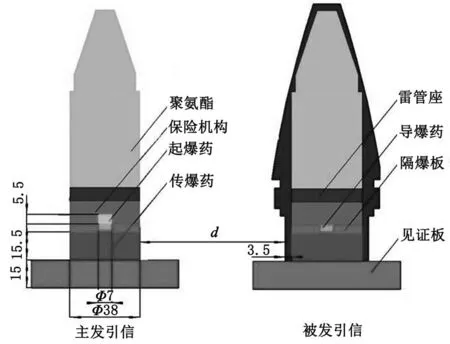
圖1 引信傳爆序列幾何模型（單位：mm）

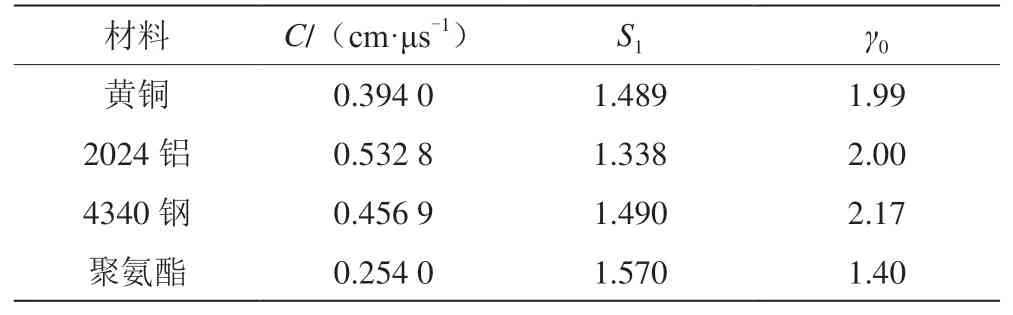
表1 紫銅、2024鋁、4340鋼與聚氨酯的格呂奈森狀態方程參數

表2 聚氨酯本構模型參數

2 結果與討論

表3為被發引信在不同距離下的爆炸情況。圖2為距離9.5 mm處25 μs、40 μs時刻被發引信不同時刻的爆炸情況。圖3為距離11.5 mm處25 μs、40 μs時刻被發引信不同時刻的爆炸情況。可見，t=25 μs時，主發沖擊波作用于被發引信，在距離為9.5 mm、11.5 mm處，被發引信都發生了反應。但是，t=40 μs時，只有距離為9.5 mm處被發引信發生了殉爆，這是因為作用于被發引信的沖擊波壓強達到了傳爆藥的臨界起爆壓強[9-12]。

表3 不同距離下被發引信爆炸情況

通過設置高斯點來獲取傳爆藥壓強變化，高斯點的選取和壓強曲線如圖4（a）所示。圖4（b）為距離9.5 mm處被發傳爆藥內部壓強歷程曲線。被發傳爆藥發生爆炸，初始峰值壓強約為7.2 GPa。隨著爆炸反應的進行，波陣面的壓強越來越高。t=26.1 μs開始，壓強值達到26.5 GPa，逐漸發展成穩定的爆轟波，直到在被發傳爆藥反應后期達到并穩定維持在JH-14C的爆壓值27.67 GPa左右。圖4（c）為距離11.0 mm處的壓強歷程曲線，可以看出t=26 μs時被發傳爆藥發生反應，爆轟波由左下向右上持續傳播，但壓強較低，初始峰值壓強僅為3.26 GPa，爆轟波繼續向右上傳播，但炸藥內部的壓強值并無上升，反而呈現衰減趨勢，被發引信未發生爆炸。

圖2 9.5 mm不同時刻引信傳爆序列爆炸結果

通過最小二乘法擬合，建立引信起爆的判據方法[13]：

式中：K、I、C為判據的擬合參數，分別有K=3.425 61、I=-8.009 58 1016、C=0.023 25；P為壓強峰值；r為引信傳爆序列之間的距離。

圖4 高斯點的選取和不同距離處傳爆藥壓強歷程曲線

3 結語

本文對引信傳爆序列在沖擊波單獨作用下的情況進行了殉爆數值模擬，得到了臨界殉爆距離和殉爆安全距離，并結合模擬結果，通過最小二乘法給出了引信起爆判據方法，可為引信傳爆序列的裝藥設計、包裝設計、生產貯存以及防護提供一定的參考。