自等價編碼與白盒實現方案的改進

羅一諾，童 鵬，陳 杰，，董曉麗

(1.西安電子科技大學 綜合業務網理論與關鍵技術國家重點實驗室，陜西 西安 710071；2.西安電子科技大學 網絡與信息安全學院，陜西 西安 710071；3.桂林電子科技大學 廣西密碼學與信息安全重點實驗室，廣西壯族自治區 桂林 541004)

在傳統密碼算法中，設計者大多只考慮了密碼算法在黑盒攻擊環境下的安全性。隨著科技的發展和敵手攻擊能力的提高，敵手不僅能訪問密碼算法的輸入和輸出，還可以獲取算法的內部細節并控制終端，使得原有的密碼算法暴露在更強的攻擊環境下。CHOW等在文獻[1]中稱此攻擊環境為白盒攻擊環境，并提出了白盒密碼來應對白盒攻擊環境。白盒密碼是以軟件的形式保護密碼算法，使得敵手在不安全的終端環境下也無法提取密鑰信息。

白盒密碼的設計主要分為兩種：一種是基于已有分組密碼的白盒實現，使用白盒密碼技術對已有的分組密碼進行改進，使其在白盒攻擊環境中具有與原密碼算法相同的功能，同時保證算法在白盒攻擊環境下的安全性。2003年，CHOW等[1]首次采用查找表、輸入輸出編碼和雙射結合的方法，將密鑰和編碼信息隱藏在查找表中，對AES進行了白盒實現；此后XIAO等[2]及LUO等[3]對AES的白盒實現分別進行了改進。KARROUMI等[4]基于CHOW等人的方案，使用對偶密碼技術設計了一種新的白盒AES。2006年，BRINGER等[5]在白盒實現中添加擾亂項設計了一種白盒AES，該實現方式與CHOW等的設計方法不同。2009年，XIAO等[6]將仿射函數與查找表技術結合，設計了SM4的白盒實現，此后也出現了多個白盒SM4的方案[7-8]。2014年，SU等[9]提出了分組密碼CLEFIA的白盒實現，此后也有多個白盒CLEFIA的改進方案[10-11]。2016年，MCMILLION等[12]首次提出基于自等價編碼的白盒AES，該方案的設計方法是白盒實現的一種新型設計方法。2020年，RANEA等[13]基于代換-置換網絡(SPN)密碼S盒的自等價，對拆分、重組后的SPN密碼的仿射層進行編碼，提出了一種通用的針對SPN結構密碼的自等價實現方案，同時提出了一種通用攻擊。2021年，王濱等[14]提出了基于AES的動態白盒實現方案。針對分組密碼的不同白盒實現的設計，先后提出了BGE攻擊[15]、MGH攻擊[16]、MULDER等[17]的攻擊、潘文倫等[18]的差分攻擊、側信道攻擊[19-20]等多種攻擊方法。另一種白盒密碼是設計白盒環境下新的分組密碼算法。2014年后，出現了新的白盒安全的分組密碼的設計，區別于傳統分組密碼以及已有分組密碼的白盒實現，它是基于某個安全的結構或某個安全目標設計的，如BIRYUKOV等[21]提出的基于ASASA結構的白盒方案，BOGDANOV等[22]提出的SPACE密碼，SHI等[23]提出的SDSRS白盒加密方案等，這些方案能保證在白盒攻擊環境下的安全性。2020年，SANDRA在其博士論文[24]中總結了白盒密碼的關鍵技術，包括白盒實現的設計、針對白盒實現的安全性攻擊以及新的白盒分組密碼的設計與分析，同時基于物理不可克隆函數(PUF)設計了一種白盒方案。

區別于基于查找表設計的白盒實現，基于自等價編碼設計的白盒實現作為一種新型的白盒實現方式值得深入研究。RANEA等[13]總結了自等價編碼設計白盒實現的局限性、白盒方案的編碼空間和適用范圍受到的限制。筆者對RANEA等的方案進行了改進，基于擴大編碼空間的思路提出了兩種改進方案，并對改進后的方案進行了安全性分析。分析表明，改進后的方案可以抵抗RANEA等提出的通用攻擊，同時基于改進方案設計的4 bit小型S盒的白盒方案的安全性也得到了提高。最后基于改進的方法設計了白盒AES，并與原方案進行了對比，證明了改進設計的安全性結論。

1 基于自等價編碼的白盒實現

在設計白盒方案前，先介紹自等價的相關知識。自等價是從BIRYUKOV等[25]提出的線性/仿射等價算法延伸出的概念。

定義1(線性/仿射等價[25]) 若S1、S2為兩個m比特變換的S盒，存在一對m比特的線性/仿射置換(A，B)，使得S2=B°S1°A，則稱S1和S2是線性/仿射等價的。

定義2(線性/仿射自等價[25]) 若S為m比特的S盒，存在一對m比特的線性/仿射置換(A，B)，使得S=B°S°A，則稱(A，B)為S的一個線性/仿射自等價。其中，A為右自等價，B為左自等價。

記SE(S)為S的全體自等價構成的集合，RSE(S)為S的全體右自等價構成的集合，LSE(S)為S的全體左自等價構成的集合。

基于自等價編碼的白盒實現[13]的思想是將SPN密碼的密鑰與線性層結合成仿射層，并使用隨機選擇的S盒的自等價對仿射層進行編碼保護，具體步驟如下。

步驟1 對SPN密碼的輪函數進行拆分、重組。將SPN密碼的輪函數表示為E(r)=LL°SL°⊕k(r)，LL為密碼的線性層，SL=S1‖S2‖…‖Sρ為密碼的S盒層，k(r)為第r輪的輪密鑰。將當前輪的LL與下一輪的k(r)結合為仿射層，即AL(r)=⊕k(r)°LL。將SPN密碼表示為仿射層與S盒層交替，如圖1所示。第1輪和第nr+1輪的仿射層分別定義為AL(1)=⊕k(r)和AL(nr+1)=LL。

步驟2 使用S盒的自等價對仿射層進行編碼：

(1)

由于自等價的特性，編碼后的仿射層與S盒交替時，中間加入的自等價編碼能被抵消，如下所示：

(2)

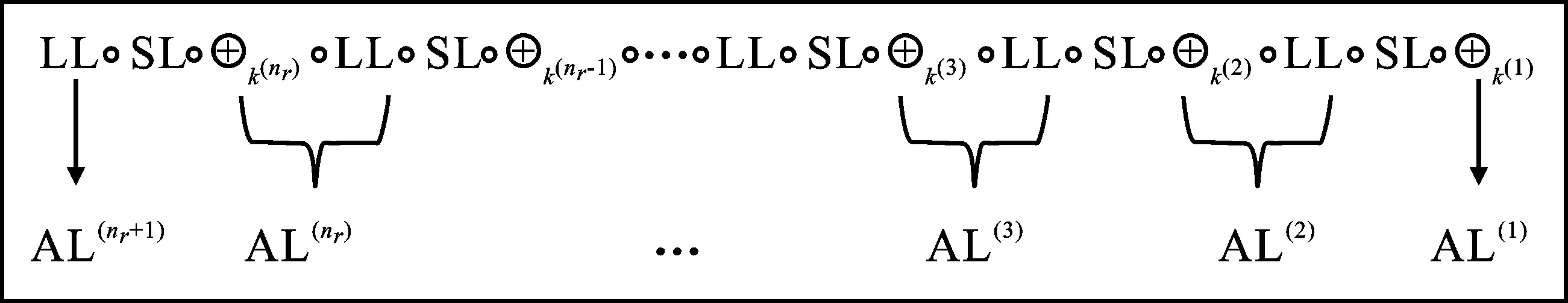
圖1 SPN密碼的加密過程

白盒方案需要加入外部編碼，防止代碼提取攻擊。因此，在算法外需要加入外部編碼，加入外部編碼后的白盒實現E′k形式如下所示：

(3)

圖2 原方案的仿射層編碼

該方案一方面利用自等價的特性使得白盒實現方案與原算法在功能上保持一致，另一方面不需要使用查找表技術，并且S盒不需要保護，因此內存占用空間大大減小，是一種新型的白盒實現。基于上述介紹的白盒實現方案，RANEA等提出了以下兩類仿射等價問題，用于討論方案的安全性。

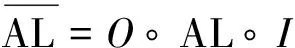
(4)

其中，Lin(g)表示取仿射函數的線性部分。Lin(Oi)作為該問題的一個特解，解集為Lin(Oi)°(C(L)∩ Lin(RSE(Si)))，其中C(L)稱為L的中心化子集合，即C(L)={A∈GLn：A°L=L°A}，GLn為包含所有n比特線性置換的一般線性群，Lin(RSE(Si))表示Si右自等價的線性部分集合，C(L)∩Lin(RSE(Si))表示上述兩個集合取交集。

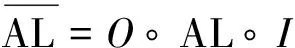
(5)

該問題包含一個特解(X0，Y0)，其中Lin(X0)=Lin(Oi)。特別地，該問題的解(X，Y)中，X滿足

Lin(X)=Lin(Oi)°( Lin(LSE(LLi，j°Sj)) ∩ Lin(RSE(Si))) 。

(6)

在文獻[13]中可看到關于這兩個問題的證明。

2 改進的自等價編碼白盒方案

筆者對RANEA等[13]的自等價編碼的白盒方案進行分析，發現白盒方案的編碼空間依賴于原SPN密碼的S盒的性質，且針對4 bit的小型S盒設計的自等價編碼的白盒方案安全性不夠理想。因此，筆者基于擴大編碼空間這一思路提出了兩種改進方案。

2.1 改進方案1

將原S盒的自等價與線性層的自等價結合為仿射層新的輸入輸出編碼，可分為以下兩步進行。

步驟1 找到n比特的可逆矩陣P和Q，使得LL=Q°LL°P，其中LL為SPN密碼的線性層，表示為n×n比特的變換。因為LL是可逆的，所以對于隨機選取的每一個可逆矩陣P，都可通過計算Q=LL°P-1°LL-1得到對應的可逆矩陣Q。

步驟2 將S盒的自等價級聯為S盒層的自等價I=I1‖I2‖…‖Iρ，O=O1‖O2‖…‖Oρ，并與線性層自等價P和Q結合。其中，單個S盒Si為m比特的變換，i=1，…，ρ，n=m×ρ。

圖3 改進方案1的仿射層

2.2 改進方案2

在原方案仿射層的外部加入線性編碼，并與S盒自等價編碼結合為仿射層新的輸入輸出編碼；同時在進入S盒層前解碼，保證加入的線性編碼能抵消，可分為以下兩步進行。

步驟2 在S盒層加入編碼，起抵消仿射層線性編碼的作用，定義加入編碼的S盒層為TL，TL=P-1°SL°Q-1，其中第r輪編碼的S盒層可表示為TL(r)=(P(r+1))-1°SL°(Q(r))-1。

考慮相鄰兩輪的輪函數，可以看到在相鄰輪中加入的自等價編碼和線性編碼可以相互抵消，從而該白盒實現方案未改變原算法的功能，如下所示：

Q(r)°O(r)°AL(r)°I(r)°P(r)=

Q(r+1)°O(r+1)°AL(r+1)°SL°AL(r)°I(r)°P(r)。

(7)

改進方案2中某一輪的仿射層如圖4所示。

3 安全性分析

為了分析自等價實現方案的安全性，RANEA等[13]提出了一種通用攻擊。攻擊思路是基于線性/仿射等價問題，將編碼空間歸約到該仿射等價問題的解集上，減小了仿射層輸出編碼的空間；進而再通過窮舉搜索和使用密鑰擴展排除錯誤的可能，恢復出密鑰。減小輪編碼空間的步驟分為兩步。

RANEA等[13]指出：對于任何SPN結構密碼算法的自等價實現方案，中心化子問題和非對稱問題是通用的等價問題，但對于其他的自等價有特殊結構的密碼，也存在其他的等價問題，進而可以利用這些問題進行歸約攻擊。

筆者通過建立中心化子問題和非對稱問題，嘗試對改進方案進行分析。分析的具體結果如下。

3.1 改進方案1的安全性分析

(1) 基于中心化子問題的歸約攻擊。首先將改進方案1仿射層的線性分塊表示為

(8)

(P-1)j，i°(LL-1)j，i°(Q-1)j，i°Lin(Oi)-1=

(9)

由于P和Q是n×n比特的可逆矩陣，它們的分塊矩陣Pi，j，Qi，j不一定可逆，中間項Pi，j與(P-1)j，i無法抵消，不能將其視作中心化子問題，自然無法將編碼空間歸約到線性層分塊的中心化子問題。因此，改進方案1可以抵抗基于中心化子問題的攻擊。

(2) 基于非對稱問題的歸約攻擊。該問題利用了自等價的特性，即一輪仿射層的輸出編碼、S盒、下一輪仿射層的輸入編碼相結合時，不改變S盒的輸入輸出，即

(10)

成立，則存在常數c使得

(11)

3.2 改進方案2的安全性分析

(1) 基于中心化子問題的歸約攻擊。首先，將仿射層的線性分塊表示為

(12)

(13)

此時可以構造類似的中心化子問題：

(14)

(2) 基于非對稱問題的歸約攻擊。在改進方案2中，編碼后的S盒層TL=P-1°SL°Q-1。根據式(10)，可得

(15)

將仿射層的線性部分與編碼后的S盒結合：

(16)

記S′=(P-1)j°Sj°(Q-1)j，即S′為被編碼的S盒。根據式(16)，可建立非對稱問題：

(17)

其中，Lin(X)∈GLm°Lin(RSE(Si))。

與基于中心化子問題進行歸約攻擊的結果類似，分塊編碼空間的大小由|GLm°RSE(Si)|變為|RSE(Si)-1°GLm°RSE(Si)°(Lin(LSE(LLi，j°Sj))∩(GLm°Lin(RSE(Si))))|。最終的歸約結果未減小分塊編碼空間，因此改進方案2可以抵抗基于非對稱問題的歸約攻擊。

3.3 分析總結

與RANEA等的方案相比，這兩種改進方案分別通過在線性層和仿射層外部加入線性編碼的方式，在一定程度上擴大了歸約后的編碼空間的大小。加入線性編碼后，改進方案1可以抵抗基于中心化子問題和非對稱問題的攻擊；改進方案2使得歸約沒有效果，從而也可以抵抗基于中心化子問題和非對稱問題的攻擊。可以看到，線性編碼的存在大大提高了方案抵抗攻擊的能力。

4 基于改進方案設計的白盒AES及安全性分析

基于上述兩種改進方式對文獻[13]中的白盒AES進行改進。筆者給出了兩種改進方案，并進行了安全性分析，最后與原白盒AES進行了對比。

4.1 方案設計

步驟1 計算AES的S盒自等價結構和數量[25]。

AES的S盒的代數表達式為S(x)=Ax-1⊕c，即先對x取GF(28)上的乘法逆元，再作用一個固定仿射函數。可以將常數c與輪密鑰結合，考慮S(x)=Ax-1。記Pd為GF(28)上的8 bit函數，定義Pd(x)=xd，因此可以得到S(x)=A°P254(x)。定義GF(28)上的函數Mα(x)=α×x，其中α∈GF28，“×” 表示GF(28)上的模多項式乘法，模多項式為f(x)=x8+x4+x3+x+1。文獻[25]中計算出S盒的自等價表達式為如下形式：

(18)

由于α有255種選擇，i有8種選擇，因此AES的S盒自等價有255×8=2 040種選擇；且從自等價的表達式可以看出，左右自等價均為線性自等價。

步驟2 對仿射層添加S盒的自等價編碼。

為了便于解釋，忽略AES輪函數中的行移位操作。記線性層LL為列混合操作對其中的一列進行的變換，對LL進行分塊：

(19)

步驟3 分別按照第2節中改進方案1和改進方案2的步驟，選取可逆矩陣P，Q與S盒的自等價結合，作為仿射層的輸入輸出編碼。

兩種改進方案如下。

(1) 采用改進方案1的設計，白盒AES的仿射層表示為

(20)

(2) 采用改進方案2的設計，白盒AES的仿射層與S盒層分別表示為

(21)

TL=P-1°(S1‖S2‖S3‖S4)°Q-1。

(22)

改進方案1使用隨機選擇的可逆矩陣對線性層進行編碼，由于P和Q是線性層LL的自等價，因此編碼后的仿射層仍與AES算法的功能保持一致；改進方案2對加入S盒自等價的仿射層進行線性編碼，同時對S盒進行編碼，用來抵消仿射層的輸入輸出編碼。

4.2 安全性分析

考慮用RANEA等提出的通用攻擊來分析基于上述改進方案設計的白盒AES，攻擊思路是對AES輪編碼的線性部分建立線性/仿射等價問題，通過構造新的仿射層編碼，將編碼空間歸約到等價問題的解集上。方案的安全性依賴于這個更小的編碼空間的基數。下面通過對AES構造中心化子問題和非對稱問題，對O1這一分塊編碼空間進行歸約并分析歸約效果。

1) 原白盒AES的安全性[13]

RANEA等基于中心化子問題，將分塊編碼空間的大小從|RSE(S)|減小到|{Mα：0≠α∈GF(28)}|，即從2 040減小到255；基于非對稱問題，可將分塊編碼空間的大小從|{Mα：0≠α∈GF(28)}|減小到|(LSE(S)∩{Mα：0≠α∈GF(28)})|。

2) 白盒AES改進方案1的安全性

由于P，Q為隨機選擇的32 bit可逆矩陣，構造

(23)

因為P和Q未知，且它們的分塊矩陣不一定可逆，因此無法得到中心化子問題，從而在這種情況下，改進方案1的白盒AES能抵抗基于中心化子問題的歸約攻擊。

3) 白盒AES改進方案2的安全性

通過對改進方案2的仿射層線性部分進行分塊，可以得到

(24)

根據式(24)建立中心化子問題：

(25)

其中，X0=Q1°O為該問題的一個特解，問題的解集為GL8°O1°(C(M3)∩(GL8°RSE(S)))。根據節3對改進方案2的分析，分塊編碼空間的大小從|GL8°RSE(S)|變為|RSE(S)-1°GL8°RSE(S)°(C(M3)∩(GL8°RSE(S)))|，即最終的歸約結果并沒有減小分塊編碼空間。因此，改進方案2可以抵抗基于中心化子問題的歸約攻擊。

因為編碼后的S盒層為TL=P-1°SL°Q-1，將仿射層的線性部分與編碼后的S盒結合，如下所示：

(26)

記S′=(P-1)3°S°(Q-1)3為被編碼的S盒，根據式(26)可建立非對稱問題：

(27)

其中Lin(X)∈GL8°RSE(S)。

該非對稱問題關于X的一個特解X0滿足Lin(X0)=Q1°O1，關于X的解集滿足Lin(X)=GL8°O1°(LSE(S)∩(GL8°RSE(S)))。根據節3的分析，分塊編碼空間的大小由|GL8°RSE(S)|變為|RSE(S)-1°GL8°RSE(S)°(LSE(S)∩(GL8°RSE(S)))|。最終的歸約結果未減小分塊編碼空間，因此改進方案2可以抵抗基于非對稱問題的歸約攻擊。將兩種白盒AES的改進方案與原白盒AES進行比較，如表1所示。

表1 兩種改進的白盒AES與原白盒AES安全性比較

從表1可以看到，兩種改進方案均擴大了分塊編碼空間，并在基于中心化子問題和非對稱問題的歸約攻擊下，改進方案1可以抵抗兩種攻擊，改進方案2使得歸約沒有效果，從而都增強了方案抵抗攻擊的能力。

5 結束語

通過添加線性編碼來擴大仿射層編碼空間，筆者對基于自等價編碼的白盒實現進行了改進，給出了兩種改進方案，并進行了安全性分析。分析表明，兩種改進方案均增大了輸入輸出編碼的取值空間，同時兩種方案均增大了歸約后的編碼空間的大小，均能抵抗針對自等價編碼的白盒實現的通用攻擊。最后，筆者基于這兩種改進的設計方法構造了兩種AES的白盒實現，并與原方案進行了對比。安全性比較結果證明了上述的分析結論。