一種新的傳感器節點分布式定位算法

徐莎莎，周 芳，李楊劍，蔣俊正，3

(1.桂林電子科技大學 信息與通信學院，廣西壯族自治區 桂林 541004；2.桂林電子科技大學 生命與環境科學學院，廣西壯族自治區 桂林 541004；3.桂林電子科技大學 廣西無線寬帶通信與信號處理重點實驗室，廣西壯族自治區 桂林 541004)

無線傳感器網絡(Wireless Sensor Networks，WSN)是由大量微小的傳感器構成的自組織網絡[1]。無線傳感器網絡中傳感器節點可以檢測監控區域中的物理信息并進行數據處理，并將處理后的數據以無線通信的方式傳送到基站[1]。無線傳感器網絡有許多應用，如醫學應用中的病人檢測[2]，環境應用中火山檢測[3]，家庭應用中用水檢測等[4]。在上述廣泛應用中，檢測到的信息需要與傳感器節點的位置結合起來，才能提供更有效的數據信息。因此，可以在傳感器中嵌入中國北斗衛星導航系統(BeiDou navigation Satellite System，BDS)模塊或全球定位系統(Global Positioning System，GPS)模塊。但這些模塊成本高，功耗大，無法適用于大規模的無線傳感器網絡。因此，選擇少量的傳感器節點嵌入中國北斗衛星導航系統或全球定位系統模塊，這些傳感器節點稱為錨節點或已知位置(Location-Aware，LA)節點，可以獲得較精確的位置信息，其他傳感器節點則稱為未知位置(Location-Unaware，LU)節點[5]。之后采用測距技術，如接收信號強度(Received-Signal-Strength，RSS)、到達時間(Time-Of-Arrival，TOA)、到達角(Angle-Of-Arrival，AOA)等測得無線傳感器網絡中傳感器節點之間的距離[5]。然后使用定位算法估計出無線傳感器網絡中LU節點的位置。

目前，已有很多定位算法被提出。從數據處理角度，可以將定位算法分為集中式定位算法和分布式定位算法。集中式定位算法將定位所需信息通過多跳的方式傳遞給存儲、計算能力較強的中央處理器進行處理。文獻[5]將定位問題歸結為無約束的優化問題，并采用修正牛頓法進行求解，得到了較好的定位精度和定位速率。但該算法計算復雜度較高。文獻[6]提出了一種集中式定位算法，將定位問題采用半正定規劃松弛的方法進行求解，將結果作為初始值，進而采用梯度下降法得出LU節點的位置，提高了定位精度。總之，集中式定位算法使用了全部的定位信息，定位精度較高，但通信代價也較高。離中央處理器較近的傳感器需要傳輸大量的信息，會較早地消耗完電量，導致整個無線傳感器網絡無法工作。而且，集中式定位算法計算復雜度較高，導致擴展性較低，無法在大規模無線傳感器網絡中使用。而分布式定位算法使用傳感器節點自帶的處理器，對收集到的局部信息進行處理，有效降低了通信代價和計算復雜度，具備良好的擴展性，可用于大規模無線傳感器網絡。文獻[7]將非凸的定位問題松弛為凸的二階錐規劃問題，利用LU節點及其鄰居信息，設計分布式二階錐規劃定位算法進行求解。該算法可用于大規模無線傳感器網絡中，但定位精度較低。文獻[8]提出了一種分布式定位算法，在每個LU節點上，將非凸的定位問題松弛為凸的定位問題，并使用梯度法進行求解，在通信半徑較小的情況下也有較好的定位效果，降低了通信代價。但該算法需要將LU節點部署在LA節點的凸包中，才能有好的定位精度。文獻[9]將無線傳感器網絡劃分為子圖，每個子圖滿足提出的剛性條件，用多維標度算法對每個子圖定位，再將局部坐標映射到全局坐標系統。該算法所需的LA節點數目較少，且劃分的子圖數目較少，定位精度較高。但當通信半徑較小，子圖無法滿足剛性條件時，無法定位。文獻[10]提出了一種基于超級節點的分布式傳感器節點定位算法，該算法將LA節點作為超級節點，對無線傳感器網絡進行子圖劃分，并進行求解。該算法有較好的定位精度，但該劃分方法難以保證劃分的子圖能覆蓋所有節點。

為了使定位算法有較高的擴展性和定位精度，能夠有效用于大規模無線傳感器網絡中，筆者提出了一種新的分布式定位算法。首先將無線傳感器網絡看作一個圖模型，將整個圖分解為部分重疊的子圖，進而將定位問題分解為一系列子圖中的優化問題。然后提出一種分布式定位算法，迭代地求解LU節點位置。每次迭代包含兩個關鍵步驟：一是LU節點位置估計，使用Barzilai-Borwein梯度法求解子圖中小規模優化問題，得到子圖中LU節點的估計位置；二是子圖融合，對部分重疊的子圖進行融合，從而得到LU節點的估計位置。筆者所提算法與集中式定位算法相比，有近似的定位精度，并通過對算法計算復雜度分析，表明這種算法計算復雜度更低，可用于大規模無線傳感器網絡中。與分布式定位算法相比，筆者提出的算法有更高的定位精度，而且對部署區域邊界的LU節點也有較好的定位效果。

1 定位問題的描述

1.1 圖模型

無線傳感器網絡是自組織網絡，可以通過無向圖G=(V，E)來描述。其中，V=V1∪V2，V1={1，2，3，…，n}表示無線傳感器網絡中LU節點集合；V2={1，2，3，…，m}表示無線傳感器網絡中LA節點集合；E={eiλ，eij}，(i=1，2，3，…，n；j=1，2，3，…，n；λ=1，2，3，…，m)表示節點之間邊的集合。其中，eiλ表示LU節點i與LA節點λ之間可以直接通信；eij表示LU節點i和LU節點j之間可以直接通信。由于受到傳感器節點功率的限制，傳感器節點只能與通信半徑R內的節點直接通信。這樣可以將無線傳感器網絡構成的無向圖劃分為部分重疊的子圖，采用以LU節點為中心將WSN劃分為部分重疊的子圖：

(1)

Gs=(Vs，Es) ，

(2)

圖1 子圖分解示意圖

其中，Vs=Vs1∪Vs2，Vs1表示子圖Gs中LU節點的集合，Vs2表示子圖Gs中LA節點集合，Es表示子圖Gs中節點之間邊的集合。如圖1所示，傳感器節點分布在[-0.5，0.5]2單位區域內，其中，圓圈表示LU節點，實心菱形表示LA節點，虛線圓表示以LU節點為圓心，R為半徑，劃分出的部分重疊的子圖。

1.2 定位問題的歸結

在監控區域Rd(d≥1)維空間中部署大量的傳感器節點，這些節點構成無線傳感器網絡。無線傳感器網絡中共有N個節點，其中有m個LA節點，n個LU節點。考慮傳感器節點部署在d=2的二維歐幾里得空間中。LA節點位置表示為aλ，λ=1，2，3，…，m；LU位置表示為xi，i=1，2，3，…，n。LU節點i與LU節點j之間的歐氏距離表示為dij，dij=dji[8]；LU節點i與LA節點λ之間的歐式距離表示為diλ。假設傳感器節點的最大通信半徑為R，則對于每個LU節點i定義兩個集合：Ni={j，dij≤R，j=1，2，3，…，n}和Mi={λ，diλ≤R，λ=1，2，3，…，m}，其中Ni表示在通信半徑R內，可以直接和節點i通信的LU節點鄰居集合；Mi表示在通信半徑R內，可以直接和節點i通信的LA節點鄰居集合。定位問題可以描述為：利用m個LA節點的位置信息、節點的鄰居信息和節點之間帶噪聲的距離信息，估計出n個LU節點xi(i=1，2，3，…，n)的位置。因此，WSN中節點定位問題可以歸結為一個無約束的優化問題[5-6]：

(3)

其中，ωij和ωiλ是權重。因為dij和diλ是帶噪聲的測距，因此給可信度較高的測距設置較大的權重；反之，給可信度較低的測距設置較小的權重[5-6]。

2 分布式定位算法

2.1 子圖內定位問題的描述

根據節1.1，將無線傳感器網絡構成的無向圖以LU節點為中心劃分為部分重疊的子圖后，可以將定位問題式(3)近似地重新構造為

(4)

其中，Es為子圖Gs中節點之間邊的集合，dij和diλ分別為子圖Gs中LU節點之間以及LU節點與LA節點之間的距離。使用RSS技術測得的距離包含噪聲，噪聲模型如式(5)、式(6)所示[6-8]。且LA節點即使加上GPS模塊，由于受到電離層誤差、對流層誤差等多種誤差的影響，得到的LA位置也是有噪聲的，噪聲模型如式(7)所示[7]。

dij=‖xi-xj‖2|1+τ1εij| ，

(5)

diλ=‖xi-aλ‖2|1+τ1εiλ| ，

(6)

(7)

式(4)中ωij和ωiλ是子圖Gs中根據節點之間距離的反比取的歸一化權重。兩個節點之間相距越近，使用RSS技術測得的距離可信度越高[11]，應賦予較高權重，反之，應賦予較低權重[5，10]。權重分別為

(8)

(9)

(10)

(11)

其中，

A=(ei1-ej1)(ei1-ej1)T+(ei2-ej2)(ei2-ej2)T，

(12)

(13)

(14)

(15)

(16)

式(4)可以改寫為

(17)

fs(x)的梯度向量?fs(x)為

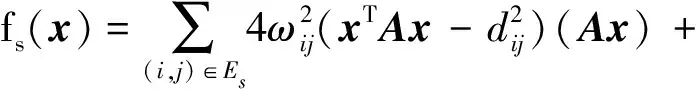
(18)

2.2 子圖求解

2.2.1 初始定位

在獲得WSN中節點之間測距信息后，采用簡單的極大似然估計法獲得LU節點的估計值[12]。目的是為了得到好的初始值。

假設D點為LU節點，坐標為(x，y)，在D點的通信半徑R內有m個LA節點1，2，3，…，m，坐標分別為(x1，y1)，(x2，y2)，(x3，y3)，…，(xm，ym)。使用RSS測距法測得D點至m個LA節點的測距分別為d1，d2，d3，…，dm。則測得的距離與D點坐標和m個LA節點坐標之間有以下關系：

(19)

將前m-1個方程與第m個方程相減，得到以下方程組：

( 20)

式(20)可寫為矩陣形式：

AX=b。

(21)

最小二乘解即為LU節點D的估計值：

(22)

在實際情況中，傳感器節點隨機部署，且受到通信半徑R的限制，很難保證每個LU節點都有3個及以上的LA鄰居。因此，筆者使用以下規則估計LU節點的初始位置：① 當LU節點有3個及以上的LA鄰居時，使用最大似然估計法計算LU節點的初始位置；② 當LU節點有低于3個LA鄰居時，將距離LU節點最近的LA節點的位置作為其初始位置；③ 當LU節點沒有LA鄰居時，將傳感器節點分布區域的中心作為LU節點的初始位置，這樣最大的初始定位誤差為區域對角線的一半。

2.2.2Barzilai-Borwein梯度法

將無線傳感器網絡劃分為部分重疊的子圖后，子圖中定位問題式(4)規模遠小于原定位問題式(3)的規模，而且使用極大似然估計法可以得到較好的初始值。因此，可以用簡單的梯度法進行優化求解，梯度法中步長的選擇會影響收斂速度[13]。采用Barzilai-Borwein梯度法，不需要進行線性搜索，僅使用當前點和前一次迭代點的信息確定步長。在每次迭代中，只需要少量的存儲和簡單的梯度計算，降低了計算量。而且與傳統的最速下降法相比，很大程度上加快了梯度法的收斂速度[13]。梯度法迭代公式如下：

xk+1=xk-αk?f(xk) 。

(23)

可將上式寫為

xk+1=xk-Fk?f(xk) ，

(24)

其中，Fk=αkI。利用擬牛頓法割線方程的性質[14]，求解以下最小二乘問題：

(25)

可以得到步長

(26)

如果k=0，則通過回溯直線搜索法確定步長α0，設置參數μ=0.2，β=0.5，α0=1，若下式成立，則令α0=βα0，繼續循環，直到下式不成立：

fs(xk+α0Δxk)>fs(xk)+μα0?fs(xk)TΔxk。

(27)

綜上所述，子圖中使用Barzilai-Borwein梯度法進行優化求解的步驟如下：

(1) 使用極大似然估計法，粗略獲得LU節點的初始值，提取子圖Gs中LU節點的位置xk，作為初始值。設k=0，表示第k次迭代；

(2) 計算搜索方向qk：qk=-?fs(xk)；

(3) 計算步長：如果k=0，則通過回溯直線搜索法確定步長α0；否則通過式(27)計算步長αk；

(4) 更新子圖Gs中LU節點位置：xk+1=xk+αkqk；

2.3 子圖融合

在構建圖模型時，將WSN構成的無向圖G以LU節點為中心分解為n個部分重疊的子圖。如圖1所示，同一個LU節點會位于不同的子圖中。因此，對每個子圖優化求解后，對于相同的LU節點會有不同的估計值。需要對子圖進行融合，從而得到每LU節點的估計值。而且可能會出現某個子圖由于可用的信息較少，導致估計出的LU節點位置誤差較大的問題。子圖融合可以有效地降低這部分節點的誤差，從而提高整體WSN的定位精度。子圖融合公式如下：

(28)

經過上述分析，分布式定位算法的整體流程如算法1所示。

算法1分布式定位算法。

準備工作：將N個傳感器隨機部署在檢測區域內，其中有m個LA節點，n個LU節點，通信半徑為R。以LU節點為中心，通信半徑內與LU節點直接相連的節點為鄰居節點，構成一個子圖。從而將WSN劃分為n個部分重疊的子圖。令t=0。

輸入：使用節2.2.1中采用的極大似然估計法及相關規則，對LU節點進行粗略的初始定位，定位結果為p(t)。將其作為步驟(1)中進行優化求解的初始值；

(1) 采用節2.2.2的Barzilai-Borwein梯度法對劃分好的子圖進行優化求解；

(2) 采用節2.3提出的子圖融合的方法，對部分重疊的子圖進行融合，得到第t+1次迭代的定位結果p(t+1)；

輸出：p(t+1)作為最終定位結果。

2.4 計算復雜度分析

3 仿真結果及分析

(29)

表1 實驗參數的設置與說明

實驗3為了研究文中算法在不同網絡規模和噪聲情況下的定位效果，本次實驗節點分布區域為[-0.5，0.5]2，改變節點總數N、通信半徑R、LA位置噪聲因子τ2進行仿真，并與文獻[5，7-8]進行對比。仿真參數設置和定位結果如表2所示。可以看出，在相同規模的無線傳感器網絡中，對LA位置添加噪聲后，各算法的定位精度均會下降。在小規模無線傳感器網絡(N<500)中，文中算法與文獻[5]提出的集中式定位算法相比，有近似的定位精度，但在大規模無線傳感器網絡(N≥500)中，集中式定位算法便無法定位，而文中算法仍有較好的定位精度，而且與文獻[7-8]提出的分布式定位算法相比，在相同的仿真參數下，始終有更好的定位精度。綜上所述，筆者提出的分布式定位算法有良好的擴展性，可有效用于大規模的無線傳感器網絡中，并且有較高的定位精度。

圖2 不同錨節點數目下的平均定位誤差

表2 文中算法與文獻[5，7-8]算法在不同參數下實驗結果對比

4 結束語

針對無線傳感器網絡定位精度較低、擴展性不高問題，筆者提出了一種分布式定位算法。首先將整個無線傳感器網絡構成的無向圖分解為部分重疊的子圖，并構造出子圖的優化問題，然后采用筆者所提算法進行優化求解。求解的過程包括子圖內的位置估計和部分重疊子圖的融合。仿真實驗證明，與現有集中式定位算法相比，有較高的擴展性，可有效用于大規模無線傳感器網絡。與現有分布式定位算法相比，有更高的定位精度。可見筆者提出的算法具備一定的優勢，可以為無線傳感器網絡的經濟、高效、實用性發展提供可靠的技術支持，進而促進無線傳感器網絡在環境科學、醫療健康等多個領域的應用。