基于最小二乘支持向量機(jī)與熵特征的地震事件性質(zhì)辨識研究

龐 聰 廖成旺 江 勇 程 誠 吳 濤 舒 鵬 丁 煒

1 中國地震局地震研究所，武漢市洪山側(cè)路40號，430071 2 地震預(yù)警湖北省重點(diǎn)實(shí)驗(yàn)室，武漢市洪山側(cè)路48號，430071 3 湖北省地震局，武漢市洪山側(cè)路48號，430071 4 運(yùn)城學(xué)院數(shù)學(xué)與信息技術(shù)學(xué)院，山西省運(yùn)城市復(fù)旦西街1155號，044031 5 南華大學(xué)計算機(jī)學(xué)院，湖南省衡陽市常勝西路28號，421001

隨著人類生產(chǎn)活動的急劇增加，距離地震臺站較近或震感強(qiáng)烈的人工爆破事件有一定概率被地震觀測儀器視作天然地震事件所記錄，產(chǎn)生的誤記錄操作將會污染已有的地震目錄甚至產(chǎn)生地震災(zāi)害應(yīng)急誤判。天然地震事件與人工爆破事件性質(zhì)辨識是當(dāng)下地震學(xué)研究及地震觀測技術(shù)應(yīng)用的重要內(nèi)容，結(jié)合機(jī)器學(xué)習(xí)或深度學(xué)習(xí)的分類決策方法在其中占據(jù)重要地位[1]。

地震事件性質(zhì)辨識的主要手段是尋找合適的地震波形特征及特征識別方法。在地震特征提取領(lǐng)域，已有學(xué)者基于時域或頻域特征深入研究，如香農(nóng)熵小波系數(shù)[2]、波形對稱度[3]、HHT提取IMF特征[4]等；在地震特征識別領(lǐng)域，常見的識別方法有決策樹[5]、支持向量機(jī)[6]、Boosting[7]、線性判別分析[8]等，但這些方法存在易過擬合、分類錯誤率較高或?qū)Χ嘀毓簿€性特征敏感等弊端。

本文首先對原始記錄進(jìn)行歸一化處理，提取排列熵、近似熵及香農(nóng)熵等特征值形成實(shí)驗(yàn)數(shù)據(jù)集，利用基于SVM改進(jìn)的LSSVM二分類方法對天然地震、非天然地震事件進(jìn)行性質(zhì)分類，采用機(jī)器學(xué)習(xí)混淆矩陣中的準(zhǔn)確率、召回率及F-measure指標(biāo)對分類結(jié)果進(jìn)行有效性評價，結(jié)合其他機(jī)器學(xué)習(xí)方法的辨識效果對比分析LSSVM算法的優(yōu)劣性能。

1 事件性質(zhì)分類方法

最小二乘支持向量機(jī)(least square SVM，LSSVM)擅長處理大規(guī)模非線性問題，數(shù)據(jù)訓(xùn)練速度較快，屬于支持向量機(jī)的改進(jìn)型方法[9]，其變化有3點(diǎn)：1)優(yōu)化目標(biāo)函數(shù)采用2NF(第2范式)；2)將不等式約束條件轉(zhuǎn)化為等式約束條件，進(jìn)而求解線性方程組，加快了求解速度，更有利于處理較大規(guī)模問題；3)對排序后的Lagrange乘子進(jìn)行裁剪處理，增強(qiáng)解的稀疏性和決策函數(shù)的適用性。

LVSVM的分類過程為：

1)對于LSSVM分類問題，約束條件是不等式約束：

yk[ωTφ(xk)+b]=1-ek,k=1,2,…,N

(1)

式中，γ為權(quán)重參數(shù)；ω為超平面法向量；ek為偏離超平面的松弛變量；φ(xk)為核函數(shù)定義的非線性映射；b為超平面的截距；yk表示線性分類一般模型{yk|yk=ω·xk+b}的分類類別，xk為訓(xùn)練樣本數(shù)據(jù)。

2)采用Lagrange乘數(shù)法轉(zhuǎn)換為求解α的極大值問題：

L(ω,b,e;α)=J(ω,e)-

(2)

式中，αk為Lagrange乘子。分別對ω、αk、b、ek求導(dǎo)，使其等于0：

(3)

根據(jù)式(3)列出關(guān)于α和b的線性方程組：

(4)

定義核矩陣Ωkl：

Ωkl=ykylφ(xk)Tφ(xl)=ykylK(xk,xl)，

k,l=1,2,…,N

(5)

3)解以上方程組可以得到α和b，最終得到LSSVM的分類表達(dá)式為：

(6)

2 數(shù)據(jù)特征提取

特征提取是展開地震事件屬性識別的重要基礎(chǔ)工作，提取的特征參數(shù)直接關(guān)系到事件性質(zhì)判斷的準(zhǔn)確性和辨識模型的合理性。本文利用信息論中的熵來表征地震事件記錄的特征。熵(entropy)是一種描述系統(tǒng)內(nèi)部混亂狀態(tài)的度量值，由克勞修斯于1865年在解決熱力學(xué)問題時提出。常見的熵值類型包括香農(nóng)熵、交叉熵、條件熵、相對熵等，已在應(yīng)用物理、生命科學(xué)、應(yīng)用數(shù)學(xué)及人工智能等學(xué)科領(lǐng)域得到應(yīng)用。地震儀器記錄到的震級較大的地震記錄具有明顯的波形統(tǒng)計特征和不規(guī)則性(局部混亂)，采用熵概念中的排列熵[10]、近似熵[11]、香農(nóng)熵[12]等表征地震事件性質(zhì)是一種新的嘗試和探討。

2.1 排列熵

排列熵(permutation entropy，Hp)是2002年由Bandt等[10]提出的，其值的大小表示時間序列的復(fù)雜程度或隨機(jī)性，值越小，信號的復(fù)雜性越低；值越大，信號的不規(guī)則性越嚴(yán)重。

設(shè)信號時間序列為{X(i),i=1,2,…,n}，進(jìn)行相空間重構(gòu)后得到如下矩陣：

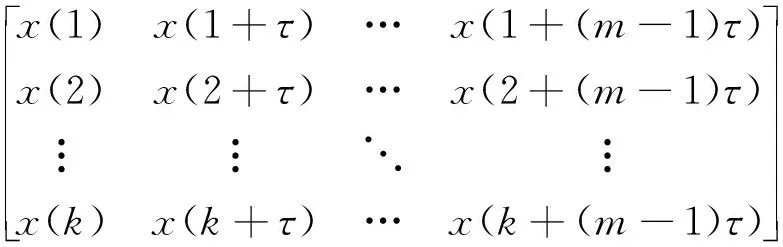
(7)

其中，m為嵌入維數(shù)，τ為延時因子，k=n-(m-1)τ,j=1,2,…,k。矩陣共有k個重構(gòu)分量，每個重構(gòu)分量有m維嵌入元素。

將式(7)中的第j個分量按數(shù)值大小升序排列，得到：

x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤…

≤x(i+(jm-1)τ)

(8)

每個重構(gòu)分量都可以得到一個重構(gòu)符號序列：

S(l)=(j1,j2,…,jm)

(9)

其中，l=1,2,…,k，滿足k≤m!。每個重構(gòu)分量是m維空間映射到m維的符號序列，共有m!種排列方式。

計算每種m維符號序列的概率P1,P2,…,Pk，根據(jù)香濃熵的定義，信號時間序列X(i)的排列熵定義為：

(10)

當(dāng)Pj=1/m!時，排列熵達(dá)到最大值ln(m!)。

2.2 近似熵

近似熵(approximate entropy，ApEn)是1991年由Pincus[11]提出的，描述m維向量擴(kuò)展至m+1維向量時的相似性或周期性度量值。作為一個非負(fù)值，ApEn的值越大，表示時序數(shù)據(jù)具有越強(qiáng)的隨機(jī)性或非周期性，可用來描述信號的復(fù)雜程度。近似熵的計算步驟為：

1)按照式(11)構(gòu)建m維向量，用y(i)表示，即{y(i),i=1,2,…,M,M=N-m+1}，其中y(i)={x(i),x(i+1),…,x(i+m-1)}，m為嵌入維數(shù)，是重構(gòu)序列的長度。計算y(i)與y(j)任意分量之間的歐氏距離d{y(i),y(j)}，并將各分量之間最大的距離定義為最大貢獻(xiàn)成分距離D{y(i),y(j)}，得到：

D{y(i),y(j)}=max{|y(i+k)-y(j+k)|}

(11)

其中，j,i=1,2,…,N-m+1；k=0,1,…,m-1。

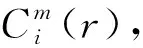
(12)

(13)

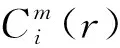
ApEn(m,r)=φm(i)-φm+1(i)

(14)

其中，當(dāng)嵌入維數(shù)m選取2或3時，有效閾值可設(shè)定為0.15倍或0.2倍的時序標(biāo)準(zhǔn)差值。

2.3 香農(nóng)熵

香農(nóng)熵H是包含平均信息量多少的度量指標(biāo)，熵值越大，說明數(shù)據(jù)中的信息量越多[12]。其定義為：

(15)

3 實(shí)驗(yàn)與分析

本文實(shí)驗(yàn)數(shù)據(jù)來源于中國地震局工程力學(xué)研究所記錄的2021年青海瑪多MS7.4地震事件與云南漾濞MS6.4、MS5.6地震事件及人工爆破事件，其中源于地震事件的三分量波形數(shù)目為158，源自人工爆破干擾事件的波形數(shù)目為342，共500份波形數(shù)據(jù)。事件及數(shù)據(jù)描述如下：

1)根據(jù)中國地震臺網(wǎng)中心測定，2021-05-21 21:21云南省大理州漾濞縣發(fā)生MS5.6地震，震源深度10 km，共有28個臺站(表1)記錄到此次強(qiáng)震動事件，其中漾濞臺震中距最小，為5.4 km，東西、南北及垂直向加速度峰值分別為-339.2 cm/s2、267.2 cm/s2、-220.1 cm/s2，計算儀器地震烈度為7.7度。

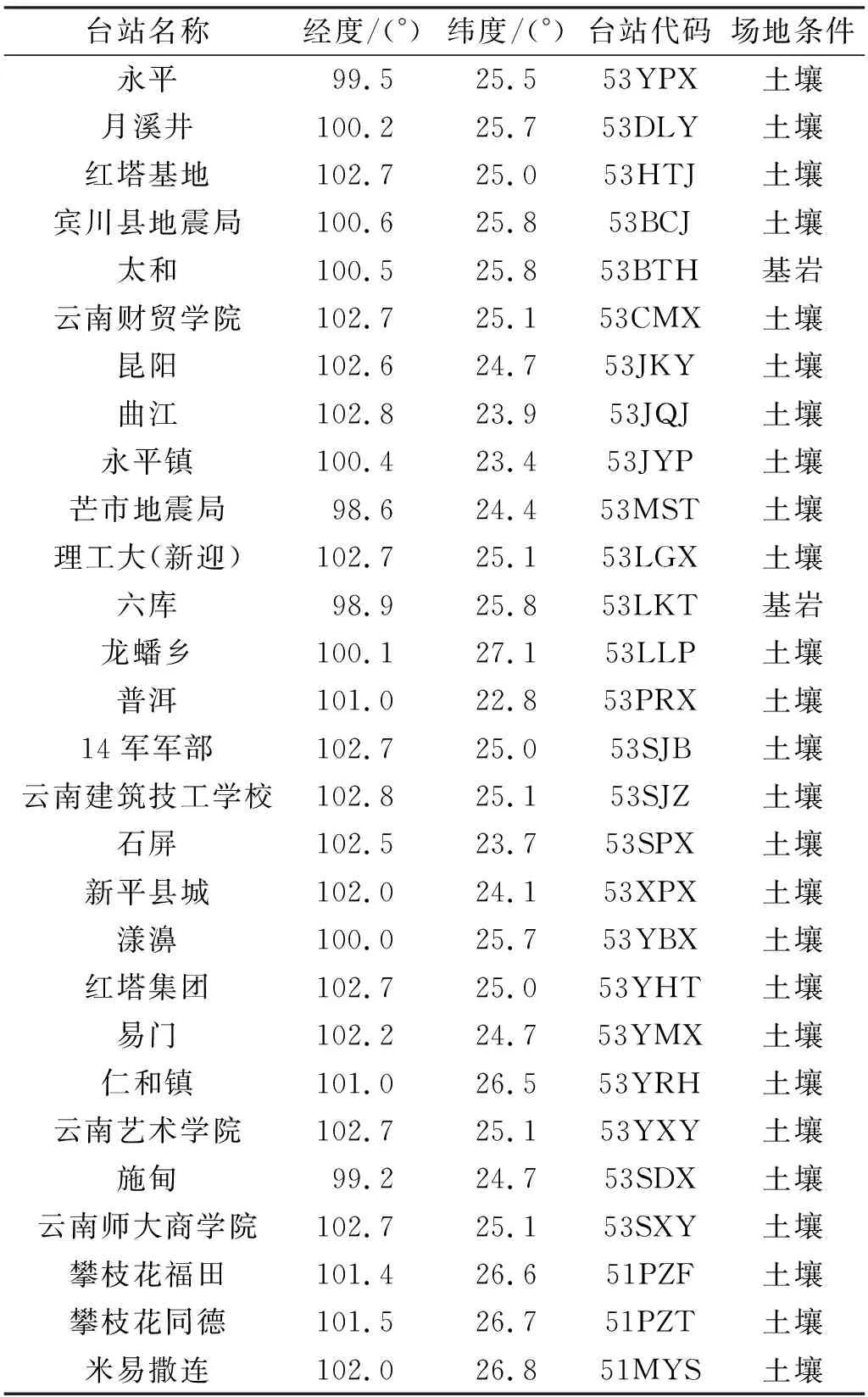
表1 云南漾濞地震事件臺站信息

2)2021-05-21 21:48云南省大理州漾濞縣(25.67°N，99.87°E)發(fā)生MS6.4地震，震源深度8 km，其中漾濞臺震中距最小，為7.9 km，東西、南北、垂直向加速度峰值分別為-379.9 cm/s2、720.3 cm/s2、-448.4 cm/s2，速度峰值分別為30.4 cm/s、-29.8 cm/s、-7.2 cm/s，計算儀器地震烈度為8.3度。

3)2021-05-22 02:04青海省果洛州瑪多縣(34.59°N，98.34°E)發(fā)生MS7.4地震，震源深度17 km，共有16個臺站(表2)記錄到此次強(qiáng)震動事件，其中大武臺震中距175.6 km，東西、南北、垂直向加速度峰值分別為46.0 cm/s2、40.6 cm/s2、-19.1 cm/s2，計算儀器地震烈度為6.0度。

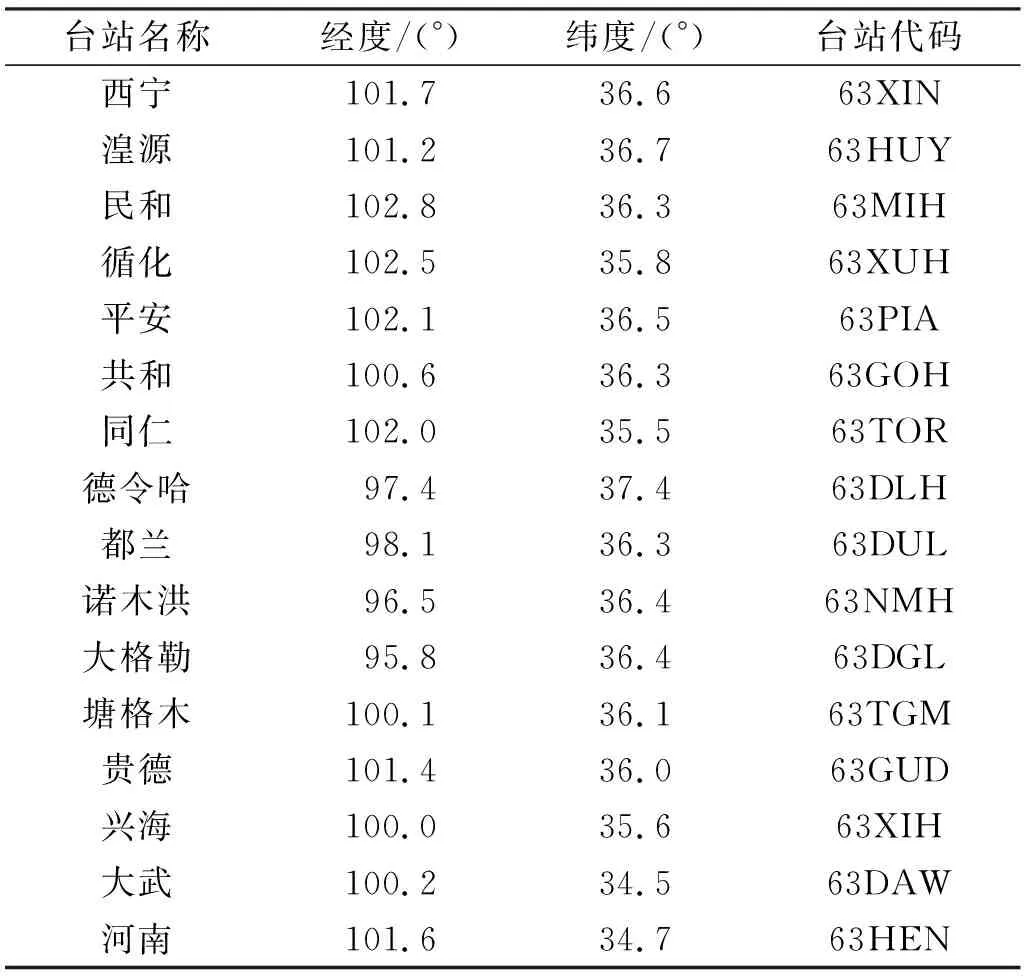
表2 青海瑪多地震事件臺站信息

4)人工爆破事件數(shù)據(jù)來自中國水利水電科學(xué)研究院巖土工程研究所，使用PCB 350B01型加速度計和PCB 350D02型加速度計進(jìn)行采集，頻率響應(yīng)為1 Hz～10 kHz，得到共計342條加速度波形記錄，記錄長度皆為40 000 m/s2。

由于每條記錄的長度(或采樣時間)及采樣頻率并不一致且差異較大，為消除幅值大小對特征工程的影響，本文統(tǒng)一取全波段數(shù)據(jù)進(jìn)行歸一化處理，并按照排列熵、近似熵、香農(nóng)熵的公式計算得到地震辨識實(shí)驗(yàn)的機(jī)器學(xué)習(xí)特征集，其中熵值計算的嵌入維數(shù)設(shè)定為2，時間延遲為1，容忍度(標(biāo)準(zhǔn)差std)為0.15，計算結(jié)果如圖1所示，統(tǒng)計結(jié)果見表3。設(shè)計多個辨識子實(shí)驗(yàn)，其中訓(xùn)練集比例分別為10%、20%、40%、60%、80%，皆為完全隨機(jī)抽取。

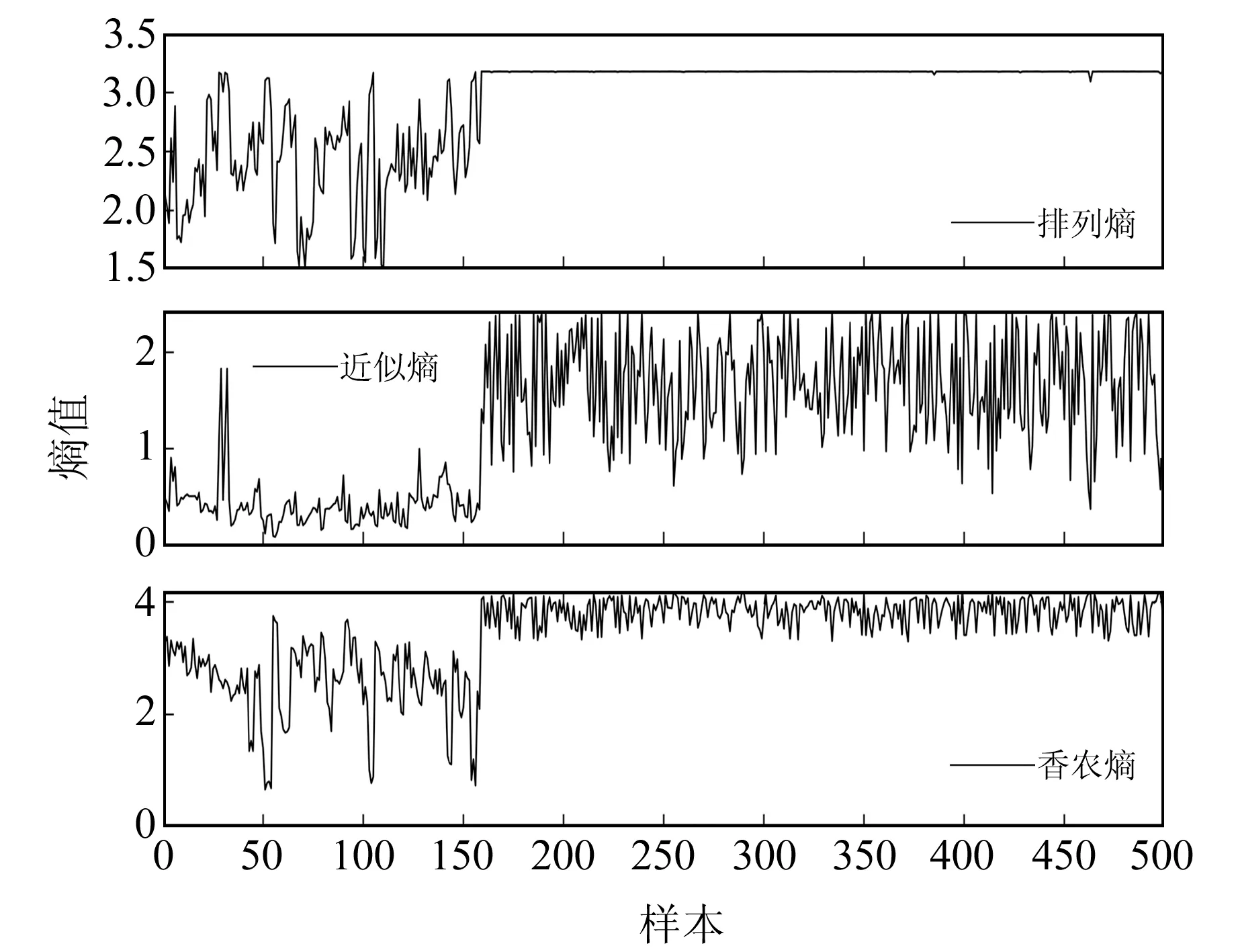
圖1 熵值計算結(jié)果Fig.1 Calculation results of entropy

表3 樣本特征集統(tǒng)計結(jié)果

結(jié)合圖1和表3可知，排列熵、近似熵、香農(nóng)熵等指標(biāo)均具有明顯的特征區(qū)分效果：在排列熵指標(biāo)上，非天然地震信號的熵值分布具有明顯的平穩(wěn)特性，標(biāo)準(zhǔn)差為0.004 9；而天然地震信號熵值則有較大的起伏變化，較不規(guī)律，標(biāo)準(zhǔn)差為0.424 6；在近似熵與香農(nóng)熵指標(biāo)上，非天然地震信號與天然地震的熵值都具有振蕩現(xiàn)象，標(biāo)準(zhǔn)差均超過0.2，但非天然地震信號的熵值期望皆比天然地震信號的大，證明該熵可用于區(qū)分二者波形。

采用機(jī)器學(xué)習(xí)混淆矩陣中的準(zhǔn)確率(accuracy)、召回率(recall)、特效度(specificity)、精確度(precision)及F-measure等評價指標(biāo)，衡量LS-SVM模型分類的有效性，核函數(shù)采用RBF函數(shù)，分類子實(shí)驗(yàn)相關(guān)結(jié)果如表4所示。

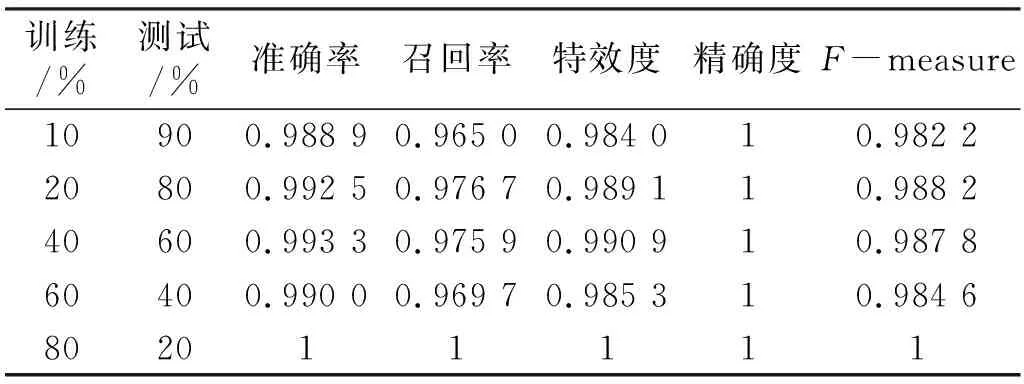
表4 LSSVM辨識實(shí)驗(yàn)結(jié)果

以訓(xùn)練集與測試集數(shù)據(jù)分別占比總數(shù)據(jù)量80%和20%為例，地震事件LSSVM模型二分類結(jié)果如圖2所示，計算得到的核函數(shù)參數(shù)為2.071 1，懲罰因子為2.307，并得到一條劃分事件波形類別較明顯的非線性超平面。LSSVM模型的輸入往往只需要二維特征矩陣即可，若為多維輸入矩陣，可由模型選擇2條特征向量繪制二分類平面結(jié)果，并自動添加與核函數(shù)類型相匹配的超平面(如采用線性核函數(shù)得到的超平面多為直線，采用多項式核函數(shù)得到的超平面多為光滑曲線，基于RBF核函數(shù)得到的超平面多為封閉曲線)。如圖2所示，橫坐標(biāo)和縱坐標(biāo)分別為測試集的排列熵與香農(nóng)熵，由超平面分割開的淺灰色地帶代表LSSVM超平面劃分的非天然地震分類區(qū)，深灰色地帶為LSSVM超平面劃分的天然地震分類區(qū)。超平面近似為凹曲線，這與非天然地震事件在分類平面上的特征映射散點(diǎn)在凹曲線上側(cè)且較為聚集的現(xiàn)象保持一致，說明模型對二者的辨識較為合理。

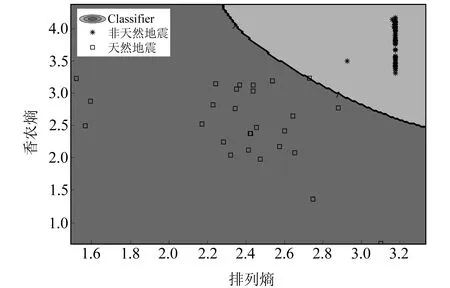
圖2 LSSVM模型二分類結(jié)果Fig.2 Two-class results of LSSVM model

為獲悉LSSVM模型在同類機(jī)器學(xué)習(xí)模型中的優(yōu)勢，選取決策樹、樸素貝葉斯、二次判別分析(QDA)、線性判別分析(LDA)及集成學(xué)習(xí)中的LogitBoost與RobustBoost等作為辨識實(shí)驗(yàn)對照方法，其中訓(xùn)練集與測試集的數(shù)據(jù)量比例均設(shè)定為4∶1，具體結(jié)果見表5。

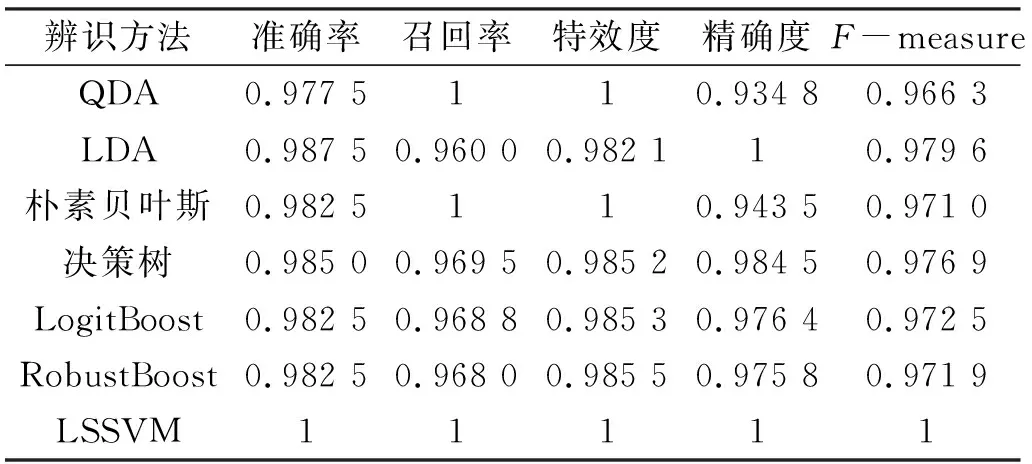
表5 機(jī)器學(xué)習(xí)模型辨識效果對比

由表5可知，在相同的訓(xùn)練集與測試集比例設(shè)置情況下，QDA、LDA、樸素貝葉斯、決策樹、LogitBoost、RobustBoost等6種機(jī)器方法的準(zhǔn)確率、召回率、特效度、精確度及F-measure值均小于或等于本文方法，證明3種熵結(jié)合最小二乘向量機(jī)的地震辨識方法具有較好的分類效果，對天然地震事件與非天然地震事件波形的區(qū)分皆達(dá)到預(yù)期，在同類方法中也有一定的先進(jìn)性。

4 結(jié) 語

本文通過對預(yù)處理后的全波段波形信號提取排列熵、近似熵、香農(nóng)熵等熵值，組建三維樣本特征矩陣，并采用最小二乘支持向量分類機(jī)方法進(jìn)行地震辨識，從而實(shí)現(xiàn)對地震事件的有效識別，得到以下結(jié)論：

1)將排列熵、近似熵、香農(nóng)熵引入地震識別中，具有一定新穎性，其特征提取結(jié)果也具有明顯的事件區(qū)分效果。

2)LSSVM模型收斂速度較快，在訓(xùn)練量較少的情況下依然可以保持較理想的識別效果，且整體識別效果要優(yōu)于QDA、LDA、樸素貝葉斯、決策樹、LogitBoost及RobustBoost等經(jīng)典機(jī)器學(xué)習(xí)方法，基于準(zhǔn)確率、召回率、特效度、精確度、F-measure等指標(biāo)的多重評價結(jié)果也證明LSSVM模型在地震識別領(lǐng)域具有一定的優(yōu)越性。

3)基于RBF核函數(shù)的LSSVM模型性能會受懲罰因子、RBF等參數(shù)的影響，在樣本學(xué)習(xí)和目標(biāo)泛化方面仍有一定的改進(jìn)空間，下一步將結(jié)合智能優(yōu)化算法對其正則化超參數(shù)進(jìn)行尋優(yōu)，增強(qiáng)LSSVM模型的穩(wěn)健性，并提高其對含噪地震樣本的非線性求解能力。另外，本文研究僅限于識別地震波形，若用于地震預(yù)警等，需要考慮辨識模型的運(yùn)算速度與預(yù)警時效，將在后續(xù)研究中對此進(jìn)行補(bǔ)充。

致謝：中國地震局工程力學(xué)研究所為本文提供數(shù)據(jù)支持，中國水利水電科學(xué)研究院巖土工程研究所提供爆破數(shù)據(jù)，在此一并表示感謝!