基于超限事件的飛行訓練品質評估模型

王帥， 陳勇剛*， 曾超

(1.中國民用航空飛行學院， 廣漢 618307； 2.四川航空股份有限公司， 成都 610225)

飛行訓練是保證飛行安全，實現民航高質量發展的基礎性工作。目前，中國民航飛行員數量已超過60 000人，每年輸入運輸航空和通用航空的飛行人才近5 000人，基本滿足中國航空業發展的人才需求。做好飛行學生訓練工作，確保培訓質量，為中國民航發展提供專業人才的支撐和保障，不僅關系到中國民航安全水平能否進一步提高，而且影響到建設民航強國的宏偉戰略目標能否實現，這也是新時代對民航飛行訓練提出的新要求[1]。近年來，民航局不斷出臺相關政策，全面深化飛行訓練改革，提出要實施“大數據+飛行訓練”戰略：以“科學分析、合理應用”為原則，加強各類數據與核心勝任能力的關聯性理論研究，積極拓寬數據源，開發多維度的飛行訓練相關數據應用平臺，以全面支撐飛行員技能全生命周期管理體系[2]。

飛行品質監控(flight operation quality assurance，FOQA)作為分析運行風險、改進訓練方法、提高訓練質量的重要手段，可以盡早地識別出超限操作、程序缺陷、航空器性能衰減等，為改進措施地制定提供數據和信息支持，在運輸航空與通用航空的飛行訓練過程中都發揮著重要作用[3]。目前，眾多學者針對運輸航空飛行品質監控數據的深入挖掘做了深入的研究。袁偉良等[4]選取起飛爬升和進近著陸階段的飛行數據記錄器(quick access recorder，QAR)數據，利用機器學習算法通過訓練粒子群算法與支持向量機(particle swarm optimization algorithm and support vector machine，PSO-SVM)模型實現飛行品質的評估；周長春等[5]利用民用飛機在進近著陸時的影響因素和QAR譯碼數據,構造出相應灰色聚類評價模型對航空公司某階段飛機進近著陸安全性進行評估；沈曉峰等[6]建立QAR數據分析的單維度模型和多維度模型,分別針對飛行員個體和機隊開展飛行品質分析；陳勇剛等[7]參考“空客飛行品質監控項目”和企業QAR監控項目,構建基于混合型中心點三角白化權函數和樹擴展樸素貝葉斯(tree-augmented na?ve bayesian，TAN)模型的運輸航空飛行安全績效模糊動態評估模型，實現對企業整體飛行安全狀態的動態掌握。在通用航空領域，飛行品質監控的實施以及監控數據的挖掘仍還在起步階段。任可等[8]對通航綜合航電系統飛參數據的篩選和清洗方法進行了詳細的介紹；張華忠[9]基于日常飛行中GARMINI1000機載SD卡的飛行數據分析，建立飛行品質監控模型。綜上，隨著通用航空飛行品質監控項目的不斷完善以及監控模型的不斷優化，為通用航空飛行品質監控數據的收集和挖掘提供了極大便利。

鑒于此，在收集C-172R、C-172S、SR20型飛機機載GARMIN1000綜合航電系統SD卡數據監控超限事件的基礎上，提出一種客觀與主觀相結合的優化組合賦權方法，結合優劣解距離法TOPSIS法和RSR法，對通用航空飛行訓練品質進行評估，以期幫助改進訓練方法，不斷提升訓練質量。

1 基于超限事件的飛行訓練品質評估指標體系

飛行訓練品質監控工作是通過收集訓練飛機機載綜合航電系統所監控的飛行參數，設定監控項目和指標進行監控，并根據監控情況動態評估飛行訓練品質和安全狀態，對于訓練管理具有十分重要的意義。正因如此，越來越多的訓練飛機都安裝了綜合航電設備，其中佳明公司的產品應用較為廣泛，如C-172R、C-172S、DA-40/42、SR-20等常見訓練機型均使用GARMIN1000系列航電系統。該系統共記錄參數60余個，參數類型較為全面，為飛行品質監控項目的確定提供了數據支持[10]。

通過機載綜合航電系統監控發現的超限事件分為偏離事件和紅標事件兩類。偏離事件的閾值設置基于《飛行運行手冊》(Aircraft Flight Manual，AFM)、《飛行員訓練手冊》(Pilot Training Manual，PTM)、實踐考試標準、安全程序與措施、運行經驗等制定，紅標事件是指在偏離事件基礎上嚴重程度更高，認為需引起足夠重視，必要時需介入事后調查的事件[11]。同時，紅標事件發生的頻次也可以用來反映訓練品質的好壞。為此，首先借鑒運輸航空FOQA經驗，確定3類一級指標，分別為技術指標X1、結果指標X2和行為指標X3；其次，在完成監控項目運算閾值設置并長期實踐驗證的基礎上，選取11項監控超限事件作為二級指標，分別為俯仰姿態超限X11、深失速/非正常失速狀態警戒X12、坡度超限X13、近地俯仰坡度警戒超限X14、低空下降率警戒/超限X15；結果指標對應的二級指標有：近地過載超限(重著陸)X21、低燃油量X22、空速超限X23；行為指標對應的二級指標有：粗猛油門操縱X31、俯仰操縱粗猛X32、連續地面等待超時X33)[12]。

2 基于方差最大化的組合賦權方法

2.1 G1法確定主觀權重

G1法是通過優化層次分析法(analytic hierarchy process，AHP)法而得到的一種無需一致性檢驗的權重計算方法[13]，計算過程相對簡便，可操作性強，同時可以充分發揮行業專家知識和經驗的優點，減少判斷誤差。具體步驟如下。

步驟1指標重要性排序。統計飛行領域專家各個指標Xi,i=1,2,…,k的打分情況，對打分結果按照重要性進行排序，其表達式為：

(1)

式(1)中:Xi*為排序后的各個指標Xi,i=1,2,…,k。

步驟2確定重要程度rn。對于重要程度，需要用數值對其進行量化。在G1法中通過rn賦值來計算。表1為G1法則常用的rn賦值范圍。

通過這些預定的取值，將各個指標的權重量化，具體公式為

(2)

表1 rn賦值參考

式(2)中：Wn為第n個指標的權重。

步驟3計算權重系數。飛行訓練中的各個指標權重系數Wz計算公式為

(3)

2.2 CRITIC法確定客觀權重

考慮到G1法受專家主觀影響較大，可能導致權重賦值上對某些指標“不公平”，不能合理又客觀地反映整個系統的“態勢”，因此，需要使用更加客觀的方式來修正G1法的缺陷。

CRITIC法是一種比熵權法和標準離差法更好的客觀賦權法[14-15]，在考慮指標變異性大小的同時可以兼顧指標之間的相關性，對于飛行訓練品質監控指標具有較強的適用性。具體步驟如下。

步驟1“0-1”歸一化。“0-1”歸一化用于消除不同指標間的量綱，同時也可以消除由于數據范圍不同帶來的誤差，具體公式為

(4)

式(4)中：x*為每一個指標歸一化后的數據；x為每一個指標原始數據；xmin和xmax分別為每一個指標所能取到的最小值和最大值。

步驟2計算標準差。對標準化后的數據，計算樣本的標準差公式為

(5)

式(5)中：σj為第j個指標的標準差；m為樣本的記錄個數；xij為第j個指標的第i條記錄；ˉxj為第j個指標的平均值。

步驟3計算指標間的相關系數。計算第j個指標和第k個指標間的相關系數rjk，計算公式為

(6)

式(6)中：Xik為第k個指標的第i條記錄；ˉXj、Xk分別為指標j、指標k的樣本均值。

步驟4計算各個指標的客觀權重Wk，計算公式為

(7)

2.3 基于方差最大化的組合賦權計算

基于歸一化約束條件下的方差最大化原理對主客觀權重進行優化組合，可以有效反映各屬性值本身的差異程度，從而使各個評估對象的評估值相對離散，使得組合賦權更加合理[16]。具體步驟如下。

步驟1構建線性規劃方程。假設：方案集X=(x1,x2,…,xn)，屬性集G=(f1,f2,…,fm)。yij=fi(xj)，是方案xj在屬性fi下的屬性值(i=1,2,…,m；j=1,2,…,n)；rij為決策矩陣Y=(yij)m×n的規范化結果。

(8)

步驟2構造Lagrange函數[17]求線性相關系數x1、x2，可表示為

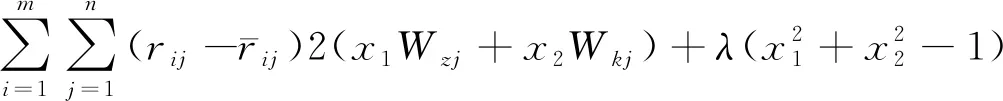
(9)

式(9)中：λ為Lagrange乘子。

(10)

(11)

3 加權TOPSIS-RSR法評估模型設計

在基于方差最大化的G1-CRITIC法組合賦權計算的基礎上，采用TOPSIS(technique for order preference by similarity to an ideal solution)-秩和比法(rank-sum ratio，RSR)法建立評估模型，對評估結果進行排序并分檔。具體流程如圖1所示。

圖1 評估模型流程圖Fig.1 Flow chart of the evaluation model

3.1 加權TOPSIS法貼進度排序

加權TOPSIS法也叫逼近理想解排序法[18]，根據已經獲取的指標權重，利用指標數據的信息，精確地對各評估方案進行綜合排序。其步驟如下。

步驟1構建初始標準化矩陣V1。首先，將X評估指標數據進行正向化處理，轉化為極大型指標(指標值越大越好)，常用的處理方法有倒數法和差值法。

步驟2構建加權標準化決策矩陣V2。為消除指標量綱影響，需對初始標準化矩陣V1進行歸一化處理，并將處理后的矩陣與組合權重做乘積運算，得到V2。

V2=(vij)m×n

=(Zjyij)m×n

(12)

式(12)中：vij為矩陣V2的第i行、第j列的值；Zj為第j個指標的組合權重系數；yij為矩陣V1歸一化處理后所得矩陣的第i行、第j列的值。

步驟3確定正理想解集V+和負理想解集V-，其表達式分別為

(13)

步驟4計算評估對象到正、負理想解的歐式空間距離，其表達式為

(14)

式(14)中：di+、di-分別為第i個參數與正理想解、負理想解的距離

步驟5相對帖近度Ci可表示為

(15)

3.2 RSR法定性分檔處理

秩和比法(RSR法)是一種比較成熟的統計分析方法，廣泛應用于醫療衛生等行業的質量評價過程。借鑒該方法的分檔思想，在TOPSIS法計算得到貼進度的基礎上，借助RSR法對研究對象進一步分檔[19-20]。

(1)Probit值的獲取。用Ci值替代RSR值排序后做頻數分布表格處理，分別計算各Ci值出現的頻數f、秩次R以及累積頻數p，結合向下累計頻數p(單位：%)查百分比與概率單位對照表得到概率單位Probit值。

(2)回歸關系分析。以Probit值為自變量、Ci值為因變量，擬合得到回歸方程，并進行顯著性驗證。

Ci=a+bProbit

(16)

式(16)中：a為常數項；b為斜率。

利用回歸方程計算Ci值，即為RSR估計值RSR。

(3)合理劃分Probit值，對RSR估計值進行分檔，確定評估對象等級。

4 飛行訓練品質評估模型實例驗證

以某飛行訓練單位為例，選取該單位2019—2021年14 個月的監控超限事件時次率作為評估樣本指標數據(表2)，對飛行訓練品質評估模型進行驗證。

4.1 飛行訓練品質評估指標組合權重計算

根據飛行領域專家打分結果，可以得出各級指標的重要性序關系，一級指標：X2>X3>X1，二級指標：低燃油量X22>空速超限X23>近地過載超限(重著陸)X21>近地俯仰坡度警戒超限X14>低空下降率警戒X15>俯仰操縱粗猛X31>坡度超限X13>深失速/非正常失速狀態警戒X12>俯仰姿態超限X11>粗猛油門操縱X33>連續地面等待超時X32；根據各個指標間的重要性比值rn，利用式(1)～式(3)計算得到一級指標權重系數W=(w1,w2,w3)=(0.206 6,0.462 8,0.330 6)，從數據可以看出，衡量安全狀態的結果指標在訓練品質評估過程中的權重系數占比較大，以規章底線為約束的行為指標比技術指標更重要，這與當前民航作風建設要求相符合；同理，可以求得各二級指標的主觀權重Wzj。由式(4)～式(7)對表2樣本數據進行分析，求得二級指標的客觀權重Wkj。由式(8)～式(11)可以求得線性規劃方程的線性相關系數x1=0.463 7，x2=0.536 3，則基于方差最大化的主客觀組合權重方程為

Zj=0.463 7Wzj+0.536 3Wkj

(17)

將Wzj、Wkj代入式(17)求得各二級指標的組合權重Zj，計算結果如表3所示。

4.2 飛行訓練品質評估結果及分檔

表2 飛行訓練品質監控超限事件數據(時次率)

表3 指標權重計算結果

表4 加權TOPSIS-RSR法飛行訓練品質評估結果

表5 飛行訓練品質評估分檔結果

4.3 評估結果展示及可靠性驗證

初期使用MATLAB快速搭建模型進行模擬，得到較好地成果反饋；搭建了一套網站可視化系統。該系統前端使用“vue+echart”開源技術；后端使用“spring cloud”搭建框架。服務啟動后，后臺應用會讀取放入固定目錄下的“.csv”數據文件，按照加權TOPSIS-RSR模型算法進行解析，求出各個擋位對應的值反饋給前端頁面進行展示，展示結果如圖2所示。

系統對14個月的飛行訓練品質進行評估，根據評估結果：2020年5月、2020年7月、2020年8月、2021年4月整體運行品質較好；2020年4月、2020年12月、2021年1月整體運行品質較差，其中2020年4月最差。同時，訓練品質變化呈現出一定的規律性，被評估對象在各學期停飛前、開飛后評估結果明顯下降；開飛后2個月內，訓練品質逐漸好轉并趨于平穩。

圖2 飛行訓練品質趨勢分析Fig.2 Trend analysis of flight training quality

經查閱該單位歷史發布的2019年12月—2020年8月月度機載SD卡監控紅標事件統計數據(圖3)，紅標事件時次率波動情況與貼近程度Ci變化相符，呈現負相關。紅標事件發生次數較多的2019年12月、2020年04月，貼近程度Ci值較小；紅標事件發生次數較少的2020年08月、2020年09月，貼近程度Ci值較大。

圖3 飛行訓練品質監控紅標事件統計Fig.3 Flight training quality monitoring red label event statistics

綜上，計算所得到的評估結果與訓練運行實際基本相符。需要指出的是，訓練品質的好壞受多方面因素影響，超限事件只是評估指標體系的一部分，以超限事件為評估指標的品質分析更加注重的是訓練飛行的安全性、規范性，對于促進依法訓練、保證訓練安全具有重要作用。

5 結論

(1)構建了基于超限事件的飛行訓練品質評估指標體系，利用歸一化約束條件的方差最大化原理對CRITIC-G1法確定的主客觀指標權重進行組合，在充分考慮主觀賦權和客觀數據的基礎上，有效反映各指標本身的差異程度，達到了優化組合賦權的目的，使指標的賦權更加科學、合理。

(2)所構建的飛行訓練品質評估模型為飛行品質評估提供了一種新思路、新方法。將加權TOPSIS法與RSR法相結合，可以有效反映訓練品質的動態變化，實現定量數據向定性特征的轉變，便于決策者更加明確的做出相關決策。

(3)搭建實際的系統，通過選取某飛行訓練單位實際訓練運行過程連續14個月的監控指標數據作為樣本，對訓練品質進行評估。評價結果與該單位月度SD卡數據分析紅標事件頻率相符，驗證了該模型的可行性和有效性。