盾構下穿及列車荷載作用下既有高鐵橋梁動力響應分析

耿大新， 譚成， 王寧， 劉宗財

(華東交通大學土木建筑學院， 南昌 330013)

近年來，中國高速鐵路建設發展迅速。隨著列車速度和負載的逐漸增加，列車通過橋梁引起振動也會增加，這將對列車的安全，穩定和舒適性產生一定的影響。因此，在列車荷載作用下橋梁的動力響應問題引起許多學者的關注[1-4]。同時盾構法以其挖掘速度快,效率高,對周圍環境的影響較小等優勢被廣泛應用于城市地鐵工程建設中[5-7]。大量穿越高速公路、鐵路等既有交通設施的施工案例時有發生，然而盾構開挖通常會對地層結構造成一定破壞，會引起既有橋梁整體結構產生不均勻沉降。當橋梁沉降過大會影響其正常使用功能和列車運行安全，形成一定的安全隱患[8-10]。

三維數值軟件因速度快，成本低，模擬結果真實等原因逐漸成為人們研究列車振動及盾構開挖常用的分析方法之一。張一鳴等[11]基于ANSYS軟件建立移動荷載模型，分析了列車荷載作用下簡支梁橋的自振特性及動力響應；宋莎嘉[12]采用移動荷載加載方式模擬列車荷載，得到了列車動荷載作用下便梁的應力與撓度值；沈銳利[13]通過建立荷載列模型，研究了同一車輛通過不同跨度簡支梁橋時橋梁跨中撓度振動響應并提出減小振動相應措施；李松等[14]運用軟件分析了盾構隧道施工時近側高架橋樁基水平位移及沉降的變形規律；王炳軍[15]利用數值分析研究了盾構施工對開挖側樁基內力和變形影響；楊才[16]通過隧道下穿既有鐵路相關實例總結隧道下穿后既有鐵路相關指標的控制限值。以上數值模擬分析大多關注列車荷載作用下橋梁的動力響應或是盾構開挖引起橋梁的變形分析，沒有考慮在盾構開挖過程中，列車動荷載作用下既有高鐵橋梁動力響應分析。

為此，依托南昌地鐵4號線一期某盾構隧道工程，通過Midas/GTS軟件建立盾構先后下穿高鐵橋梁的有限元模型，對盾構開挖時不同速度、軸重以及盾構不同開挖階段時列車荷載作用下既有高速鐵路簡支梁橋梁墩頂變形進行分析，對于今后類似項目的處理具有一定的參考價值。

1 工程概況

1.1 地鐵與橋梁的位置關系

南昌市軌道交通4號線一期工程東新站到新洪城大市場站區間下穿兩條相互平行的滬昆高鐵贛江特大橋與昌福鐵路贛江特大橋。其中滬昆高鐵是作為客運專線，設計行車時速為350 km/h，昌福鐵路是一條客貨聯合共線的高速鐵路，設計時速200 km/h。地鐵線與既有鐵路夾角約為88°，如圖1所示。

盾構左右線先后開挖。采用混合式土壓平衡盾構法施工，管片內徑5.4 m，外徑6.0 m，厚度300 mm，環寬1 200 mm。下穿段鐵路橋均為兩聯32 m預應力混凝土簡支梁橋，左右線各穿橋梁一跨，穿越滬昆高鐵贛江特大橋977#～979#橋墩，昌福鐵路贛江特大橋100#～102#橋墩。如圖2所示，隧道左線距滬昆高鐵978#橋墩最近距離為7.46 m，隧道右線距昌福鐵路101#橋樁最小靜距8.11 m，隧道頂部埋深約為14 m。

#為橋墩編號，以99#為例，表示99號橋墩圖1 盾構穿越平面圖Fig.1 Shield crossing plan

圖2 盾構下穿鐵路橋梁橫斷面示意Fig.2 Cross-section of a railway bridge under the shield

1.2 工程地質條件

自上而下對于地層的具體描述可以分別為：素填土、粉質黏土、中砂、粗砂、礫砂、強風化泥質粉砂巖、中風化泥質粉砂巖。填土與礫砂為主要含水層，地面30 m以下區域以中風化泥質粉砂巖為主，盾構主要貫通于礫砂層之間。各土層參數如表1所示。

表1 土體力學參數

2 數值模型建立

2.1 隧道數值模型建立

根據盾構隧道與鐵路橋梁的位置關系采用Midas/GTS軟件建立三維數值模型，隧道結構外左右邊界，即模型x方向取200 m，隧道結構上下邊界，取隧道開挖洞徑5倍左右，即模型z方向范圍取60 m，縱向開挖線y方向取100 m，采用混合網格對單元進行網格劃分，計算整體模型如圖3所示。盾構隧道穿越橋梁及墩臺編號示意如圖4所示。

模型中基于摩爾-庫倫準則對地層進行模擬，橋樁采用梁單元模擬，土體、高鐵橋梁墩臺用實體單元模擬。盾構開挖區域管片、盾殼、注漿等定義為彈性材料分別采用實體與板單元模擬，如圖5所示，隧道結構及橋梁墩臺材料參數如表2所示。橋樁與墩臺實體接觸節點在Midas/GTS中通過印刻命令實現節點耦合，橋樁和土體之間設置樁界面單元模擬樁土之間接觸。

圖3 盾構下穿整體模型Fig.3 The overall model of the shield tunneling

圖4 盾構隧道推進過程模型及橋梁墩臺編號Fig.4 Shield tunnel advancing process model and bridge pier number

模型中對滬昆高鐵及昌福鐵路特大橋橋梁的上部結構進行簡化模擬如圖6所示，對兩橋橋梁箱型截面梁用實體單元模擬，墩臺與主梁接觸節點設置為彈性連接。

兩橋軌下結構都采用CRTSIII型板式無砟軌道進行簡化模擬，底座板、自密實混凝土、軌道板等采用實體單元模擬。如圖7所示，按照文獻[17]規定橋梁各上部結構材料參數如表3所示。

圖5 盾構隧道模型構件Fig.5 Shield tunnel model components

表2 模型材料參數

圖6 橋梁上部結構整體模型Fig.6 Overall model of bridge superstructure

圖7 橋梁上部結構模型構件Fig.7 The upper structural model components of the bridge

2.2 特征值分析

動荷載分析前首先需對模型進行特征值計算，在Midas/gts數值分析中，可直接通過建立地面彈簧單元生成彈性邊界進行特征值分析。為了探討盾構開挖時列車動荷載的影響因此將盾構分主要分為4個階段，并對每個開挖階段進行特征值分析，算得各開挖階段下特征值如表4所示。

表3 橋梁上部結構材料參數

表4 開挖階段主振型周期

2.3 荷載與邊界條件

對模型施加列車動力荷載，采用移動的列車動力荷載[18]對鐵路列車進行模擬。如圖8所示，根據滬昆高鐵與昌福鐵路列車運行的方向選擇開始和結束的節點，同時考慮到列車車輪兩邊都有，對列車荷載采用對稱布置。

圖8 移動列車荷載布置Fig.8 Load arrangement of mobile train

在動力分析時，采用Lysmer等[19]提出的黏性邊界條件，在定義黏性邊界時，根據巖土材料輸x、y、z方向阻尼值并計算。阻尼值計算公式為

看了這一條，讀者通過邏輯思維必然會覺得“原來鵝鼻山就是秦望山！秦始皇是登上鵝鼻山‘以望南海’的！”但再一想又不對了：大越不會有兩座秦望山，前一條說山在縣東南四十里，入城者已經難以看到它，現在搬到縣西南七十里，使涉境者更難見到了。

(1)

(2)

在Midas/GTS數值分析中通過“地面彈簧”生成黏性邊界。

3 列車荷載作用下橋梁動力響應分析

盾構穿越既有高鐵橋梁施工時，上方列車行駛時會產生動應力，對既有橋梁和鐵路結構的沉降有一定的影響。根據文獻[20]，在一定范圍內，列車動應力和列車速度和車輛軸重呈線性增加的關系。針對當盾構開挖至高鐵橋梁近側時，對不同速度、軸重列車沖擊作用下橋梁的變形規律進行研究，同時對不同開挖階段下列車荷載引起高鐵橋梁的變形情況進行分析。

3.1 分析步與測點設置

按照圖9提取模型數據，從滬昆高鐵贛江特大橋976#～980#橋墩和昌福鐵路贛江特大橋99#～103#橋墩上各取其5個墩臺頂中心點，共10個數據點，其中滬昆高鐵墩臺中心點①～⑤，昌福鐵路特大橋墩臺中心點⑥～⑩。

圖9 模型數據提取點Fig.9 Model data extraction points

由兩橋均為四聯32 m簡支梁橋，列車以200 km/h通過模型中橋梁區域所用時間約為2.4 s，依此保守計算，將移動列車荷載的分析步時間設為3 s，即動載分析步總時長為3 s，積分步時長Δt=0.03。

3.2 車速對高鐵橋梁動力響應影響

由圖10(a)可知，當列車以350 km/h過橋時，③號墩臺中心點產生的位移時程曲線呈波動性，且在0.8 s左右達到峰值，其中盾構未開挖時墩臺中心點產生的最大沉降約為1 mm，盾構開挖時產生的最大沉降約為3.7 mm且沉降波動穩定在2 mm。由圖10(b)可知，速度為300 km/h時，沉降在1 s左右達到最大值，盾構未開挖與開挖時產生的最大沉降分別為0.8 mm和3.5 mm，其開挖后沉降波動穩定在1.8 mm。由圖10(c)知，速度為250 km/h時，沉降在1.3 s左右達到最大值，產生的最大沉降分別為0.8 mm和3.2 mm，其開挖后沉降波動穩定在1.8 mm。如圖10(d)所示，當列車為200 km/h，其沉降在1.5 s時達到峰值，盾構未開挖與開挖時產生的沉降峰值分別為0.8 mm和2.8 mm，沉降波動穩定在1.5 mm。整理4種速度下，墩臺中心點③的沉降峰值如表5所示。

表5 墩臺沉降峰值及發生時刻

數值計算結果顯示，當盾構隧道開挖至兩高鐵橋梁近側時，軸重為170 kN的列車4種速度沖擊下，橋梁墩臺頂的變形規律基本一致，墩臺中心點沉降在一定時間的達到峰值，其后墩頂沉降迅速降低并穩定在某一波動范圍內。由表5可知，隨著列車速度越快，墩臺中心點的沉降峰值越大，當列車速度降至200 km/h，墩頂沉降最大值滿足《公路與市政工程下穿高速鐵路技術規程》(TB 10182—2017)[21]。

3.3 車速對高鐵橋梁動力響應影響

同樣以跨徑為32 m的滬昆高鐵贛江特大橋跨中墩臺中心點3(978#)為分析對象，當盾構左線開挖至兩橋中間，車速為200 km/h時，對220、180、110 kN三種列車軸重沖擊作用下的滬昆高鐵贛江特大橋跨中墩臺中心點③的位移變化進行分析。與速度分析相同，每組車重也分為兩種工況，不同列車荷載下其墩臺中心點③的位移時程曲線如圖11所示。

由圖11(a)、圖11(b)可知，當盾構左線開挖至兩橋中間且車速為200 km/h時，車重為220 kN盾構開挖時，產生的最大沉降接近6 mm，未開挖時沉降約為1.3 mm且波動很小。車重180 kN時開挖時產生的最大沉降約為4.5 mm，未開挖時沉降波動趨勢與200 km/h相似；如圖11(c)所示，當車重110 kN時，產生的最大沉降為2 mm，最大沉降滿足高速鐵路單墩頂豎向沉降3 mm標準，未開挖時最大沉降小于1 mm波動趨勢與前者相似。整理3種軸重下，墩臺中心點③的沉降峰值如表6所示。

圖11 各車重下墩臺中心點③位移時程曲線Fig.11 Time-history curve of displacement of center point ③ of pier under each vehicle weight

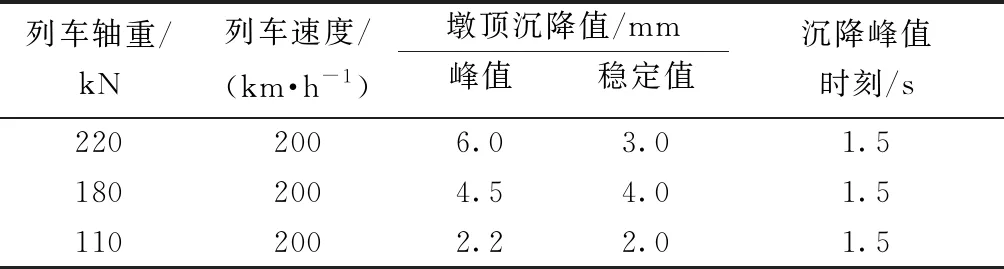
表6 不同軸重墩頂沉降峰值

從橋梁墩臺中心的沉降的分析來看，當盾構隧道開挖至高鐵橋梁近側時，與列車速度相比，列車軸重對橋梁墩頂變形影響更大且軸重越大，沉降峰值越大。同時由表6可知，當列車速度為200 km/h，軸重為110 kN時,墩頂沉降峰值才滿足橋梁單墩頂3 mm沉降標準且留有較大的變形余量。

3.4 不同開挖階段列車荷載對高鐵橋梁的影響

為便于分析不同開挖階段下列車荷載對高鐵橋梁的影響，結合速度、軸重的分析選取速度為200 km/h，軸重為110 kN的列車，將盾構開挖作為唯一變量分為4個主要施工步，施工步設置如表7、圖12所示。

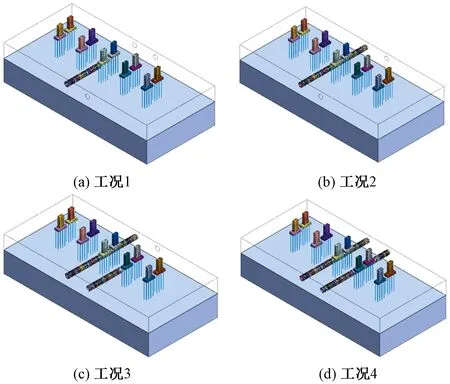
圖12 工況設置俯視圖Fig.12 Top view of working condition setting

盾構開挖至主要施工步列車運行時，對模型中兩橋10個墩臺中心點沉降變化進行分析，列車運行1.5 s時鐵路橋梁墩臺頂的沉降位移云圖如圖13所示。

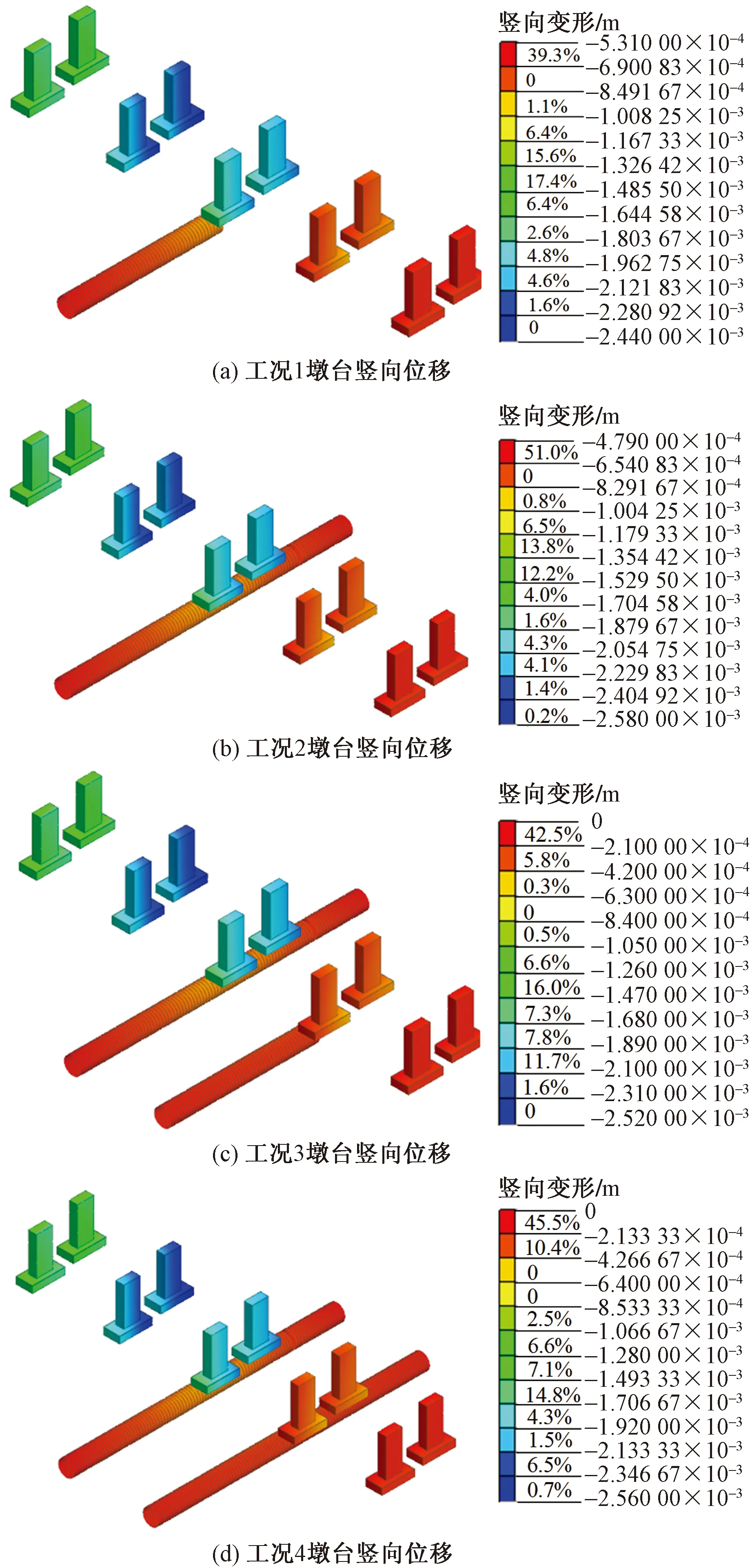
圖13 各工況下墩臺豎向位移變化Fig.13 Changes in vertical displacement of the platform under each operating condition

從盾構開挖階段來看，當盾構左線掘進至兩橋中間時，由于隧道開挖及列車荷載的共同影響下對既有橋梁的墩臺整體均發生沉降，其最大值位于盾構左線開挖近側的墩臺中心⑧，為2.2 mm。當盾構左線開挖完成時，墩臺整體沉降及沉降峰值并無明顯變化。

當右線開挖至兩橋中間，整體沉降值略有增大，沉降峰值2.2 mm，位于右線開挖近側墩臺中心④，而墩臺中心⑧沉降為1.7 mm，與左線開挖時相比略有減小；盾構右線開挖完成時，列車荷載作用下橋梁各墩臺中心點的沉降基本處于穩定狀態，墩臺整體沉降及沉降峰值并無明顯變化。整理4種工況下，墩臺中心點(①～⑩)的沉降變化及沉降峰值分別如表8、圖14所示。

從4個不同的開挖階段，速度為200 km/h，軸重為110 kN的列車荷載沖擊下橋梁墩臺變形情況來看，盾構開挖與列車荷載對橋梁變形主要影響階段為盾構開挖至橋梁近側時，即盾構初開挖階段。由圖14可知，當盾構右線開挖至一定階段時，盾構左線開挖近側沉降值略減小，這可能與盾構左線后期管片安裝及注漿有關。

表7 工況設置

表8 各工況下墩臺最大沉降值

圖14 墩臺中心點豎向位移變化Fig.14 Vertical displacement changes at the center point of the platform

圖14曲線還反映出：滬昆鐵路橋墩臺中心點①、⑤與昌福鐵路橋的⑥、⑩墩臺中心點位于開挖區域遠側，沉降變形穩定在1 mm內，與未開挖時列車荷載作用產生的沉降變化相似。由此可看出列車荷載作用下盾構開挖影響范圍約為5D(D為盾構直徑)。

4 結論

(1)盾構開挖至橋梁近側時，不同速度、軸重列車荷載沖擊下，高鐵橋梁墩臺頂的變形規律基本一致，其沉降在一定時間達到峰值，其后逐漸回升并穩定在某一波動范圍內。列車速度越快，軸重越大，其墩臺中心點的沉降峰值越大。

(2)與列車速度相比，列車軸重對橋梁的動力響應影響更大。可知，當盾構開挖時，當列車時速低于200 km/h、軸重小于110 kN時其墩臺頂沉降峰值才滿足高鐵橋梁單墩頂豎向沉降控制標準，且擁有較大的變形余量。

(3)列車動荷載作用下，盾構隧道開挖對橋梁墩頂變形的影響主要為盾構開挖至橋梁近側的初開挖階段，盾構開挖遠離橋側后墩頂變形基本處于穩定狀態。盾構開挖影響范圍約為5D。

(4)為減少列車動應力對鐵路橋梁和鐵路結構的影響，盾構開挖時對列車進行限速和限重能夠起到一定控制沉降的作用。