摻雜和應變對硅納米線電子結構與光學性質的調制影響

張加宏， 王超， 劉清惓， 顧芳， 李敏

(1.南京信息工程大學江蘇省大氣環境與裝備技術協同創新中心， 南京 210044; 2.南京信息工程大學物理與光電工程學院， 南京 210044)

硅納米線(silicon nanowires, SiNWs)因其獨特的性能和潛在的應用前景受到了人們的廣泛研究[1]。如采用硅納米線陣列替代薄膜等材質作為太陽能電池的吸收層[2]，利用SiNWs大的比表面積實現新型氣敏材料[3- 4]，通過SiNWs巨壓阻特性來提升壓敏傳感器的檢測靈敏度[5]，可見SiNWs已成為重要的光電與力電耦合材料[6-7]。隨著科技持續發展，人們逐漸將研究方向拓展到各類摻雜SiNWs以提高其光電和力電性能，其中典型的摻雜手段包括空位摻雜和元素摻雜。在量子尺寸效應下，不同類型摻雜會導致SiNWs能帶結構發生變化，從而可以調制其光電性質。梁偉華等[8]研究發現，Ni原子摻雜時其更容易占據SiNWs內部的六角形間隙位置，而通過改變Ni摻雜濃度可調控SiNWs的帶隙、光吸收強度與寬度。此外，SiNWs表面存在大量未飽和的懸掛鍵，暴露在空氣中表面的硅原子會被自然氧化為二氧化硅，這導致一定的軸向應變施加于SiNWs，影響它的能帶結構與光學性質[9-10]。因此研究單軸應變如何改變摻雜SiNWs的光電性質也具有重要的意義。

為此，以[111]晶向六邊形截面的SiNWs為研究對象，利用基于密度泛函理論的第一性原理方法，研究了單軸應變作用下空位摻雜與元素摻雜對SiNWs電子結構與光學性質影響，并對計算結果及其變化規律做出詳細分析，以期為實驗研究提供相關的理論參考。

1 摻雜SiNWs結構模型與計算方法

1.1 摻雜SiNWs結構模型

首先應用Material Studio 7.0中的Visualizer模塊建立Si晶胞，它的晶格常數為5.431 ?，然后沿[112]晶向切割Si晶體得到Si納米薄膜，再沿[100]晶向切割Si納米薄膜，獲得沿[111]晶向的SiNWs，如圖1所示，其截面為六邊形。圖1(a)為去除一個Si原子的空位摻雜SiNWs的示意圖，圖1(b)為去除兩個H原子的空位摻雜SiNWs的示意圖，圖1(c)為元素替代摻雜兩個B原子的SiNWs的示意圖，圖1(d)為[111]晶向SiNWs的側面圖。x軸方向(即長度方向)為SiNWs模型的周期性方向，y和z方向的兩相鄰表面間加12 ?的真空層，這樣可忽略相鄰兩層原子間的相互作用力，且沿y和z方向上表面的懸掛鍵均采用H原子鈍化，以得到穩定的最小能量值。圖1中SiNWs的直徑為14.7 ?，x方向的晶格常數為12.9 ?。

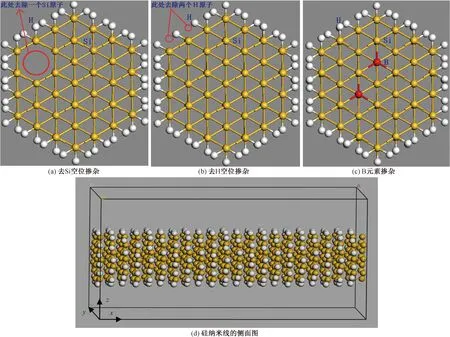
圖1 空位摻雜及元素摻雜[111]晶向SiNWs幾何模型的截面圖與側面圖Fig.1 Cross-sectional and side views of the geometric model of vacancy doping and element doping SiNWs along the [111] direction

為了研究應變對摻雜SiNWs電子結構與光學性質的調制影響，選擇摻雜SiNWs作為研究對象施加單軸應變。對于直徑小于10 nm的SiNWs，在彈性限度范圍內，施加應變一般不能超過10%，因此在SiNWs的x軸方向所加應變為±10%，正應變表示拉伸，負應變表示壓縮，應變ε計算公式為[10]

(1)

式(1)中：a0為無應變時SiNWs沿x軸方向的晶格常數；a為應變后x軸方向的晶格常數。

1.2 計算方法

第一性原理的計算工作都是由Material studio中的CASTEP軟件包完成[11]。采用超軟平面波贗勢和GGA/PBE(generalized gradient approximation of Perdew-Burke-Ernzerhof)交換關聯能[12]，幾何結構優化法使用BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法，平面波截止能設置為340 eV。自洽收斂精度設置為每個原子2×10-5eV，原子的最大位移收斂標準設為0.002 ?，布里淵區K點網格數為6×1×1，原子間的相互作用力不超過0.05 eV/?，晶體內應力收斂標準為0.1 GPa，原子的最大位移收斂標準為2.0×10-4nm。基于優化幾何結構計算能帶結構和光學性質，選擇Norm-conserving贗勢，取較高的截止能為350 eV，布里淵區K點網格數取6×1×1。施加應變時SiNWs結構優化方法和性質計算方法設置與無應變時相同。

2 計算結果與討論

2.1 應變作用下摻雜SiNWs的電子結構

圖2展示了無應變時摻雜SiNWs沿布里淵區高對稱點G-B方向的能帶結構，可以看到摻雜顯著改變了SiNWs的能帶結構。本征[111]晶向SiNWs的直接帶隙為1.67 eV，去除一個Si原子的空位摻雜SiNWs的帶隙減小為1.5 eV，且轉變為間接帶隙材料；去除兩個表面鈍化H原子，空位摻雜體系中多出兩個電子，形成N型半導體，在費米能級附近產生了兩條電子雜質能級。由于導帶底部向費米能級靠近，使得帶隙變窄、導電性增強；元素摻雜兩個B原子后，P型體系中多出兩個空穴，從圖2中可看到雜質能級跨過費米面，表明B原子摻雜SiNWs為P型直接帶隙半導體。歸因于導帶底上移，材料帶隙變化較小，但考慮到部分價電子參與導電，因此該體系導電能力也有所增強。

G、B為布里淵區高對稱點圖2 無應變時摻雜SiNWs的能帶結構Fig.2 Band structures for the doping SiNWs without strain

G、B為布里淵區高對稱點圖3 壓應變時摻雜SiNWs的能帶結構Fig.3 Band structures for the doping SiNWs under compressive strain

圖3給出了摻雜SiNWs在施加-10%壓應變后的能帶結構。不難發現所有SiNWs價帶頂和導帶底均位于G點，屬于直隙半導體，且壓應變明顯減小了帶隙。去除Si原子的空位摻雜SiNWs在費米面附近產生兩條缺陷能級，但其能級曲率明顯變小、空穴載流子質量大，影響導電能力；壓應變對去除兩個H原子的SiNWs的價帶影響較大，價帶上移和導帶下移導致帶隙減為0.5 eV，體系導電能力顯著增強；歸因于雜質能級跨越費米面，壓應變同樣使得B原子摻雜SiNWs的帶隙減小，導電性增強。

圖4為10%拉應變作用下摻雜SiNWs的能帶結構圖，所有SiNWs價帶頂和導帶底均位于G點，也屬于直隙半導體材料。拉應變對本征和元素摻雜SiNWs的帶隙影響很小，但卻顯著改變了它們價帶頂的曲率，不難發現能帶曲率明顯減小，這意味著空穴載流子質量明顯變大，導電性急劇減弱，從而形成良好的壓阻特性[10]。與壓應變作用效果類似，拉應變明顯減小了空位摻雜SiNWs的帶隙，不同的是部分價帶在拉應變下內部發生交換位置現象，這些變化無疑會導致不一樣的光學性質。

圖4 拉應變時摻雜SiNWs的能帶結構Fig.4 Band structures for the doping SiNWs under tensile strain

2.2 應變作用下摻雜SiNWs的光學性質

介電函數ε(ω)是溝通帶間躍遷微觀物理過程與材料電子結構的橋梁，其為頻率ω的函數，可表示為

ε(ω)=ε1(ω)+iε2(ω)

(2)

式(2)中：ε1(ω)和ε2(ω)分別為介電函數實部和虛部，主要表征軌道能級電子占有態與非占有態之間的躍遷，通過它們可以方便地得到其它各種光譜信息。

圖5為摻雜SiNWs的介電函數實部隨著光子能量變化的曲線。理論計算得到本征SiNWs的靜態介電常數ε0=1.44，在0～5 eV低能段介電函數實部ε1(ω)隨光子能量的增加呈現出先緩慢增大后迅速減小再增大的趨勢，當能量約為3 eV時達到最大值，表明在此之后帶間電子躍遷光吸收顯著增強。空位摻雜對ε1(ω)的影響較小，而元素摻雜則顯著提高了靜態介電常數，但低能區介電數值整體上下降，表明體系的導電性有所提升。拉應變和壓應變均增加了體系的靜態介電常數。拉應變使介電峰向低能區紅移，并且峰值增加，表明體系導電能力被削弱。與之相反，壓應變則降低了介電峰幅值，表明體系導電能力有所增強。這些均與前面能帶結構分析結果相吻合，同時也表明單軸應變能夠有效調制體系的介電與導電性能。

圖5 應變作用下摻雜SiNWs的介電函數實部Fig.5 The real part of dielectric function for the doping SiNWs under different strains

圖6為摻雜SiNWs的介電函數虛部隨著光子能量變化的曲線。可以看出，無應變作用時，本征[111]晶向SiNWs在0～1.6 eV紅外區域，ε2(ω)數值基本為0，當能量達到3.92 eV時，ε2(ω)達到最大值1.52，該介電峰主要由價帶頂占據態到導帶底非占據態的電子躍遷產生。去H原子與摻雜B原子的SiNWs在0～1.44 eV光子能量范圍出現了新的介電峰，去H的空位摻雜SiNWs的介電峰位于0.18 eV處，B原子摻雜的介電峰在0.16 eV處，且為最大的躍遷峰，峰值約3.4 eV。在2～6 eV的可見光與紫外光區域內摻雜SiNWs均存在介電峰，去H與摻雜B的介電峰基本重合，去除Si原子的介電峰峰寬相比其他三者更大。在施加10%拉應變后，摻雜SiNWs的介電峰大幅升高，所處的能量范圍向低能區擴展，介電峰明顯紅移，其半高寬比無應變時增加了一倍，出現了明顯的寬化現象，表明拉應變的引入能夠有效改善SiNWs的吸收寬度。去除Si原子的空位摻雜SiNWs在光子能量為3.1 eV時，ε2(ω)達到最大值1.9。去除H原子的空位摻雜SiNWs的ε2(ω)在2.93 eV處達到最大值2.07，展寬為四者中最寬。B原子摻雜SiNWs的ε2(ω)在光子能量達到3 eV處達到最大2.02。可以看出，在0.13 eV附近，摻雜SiNWs的介電函數虛部均出現了幅度為0.5的介電峰。在施加-10%壓應變后，摻雜SiNWs的主峰值大幅減小，介電峰的半高寬也有所減少，且介電峰發生紅移。由此可見，施加拉應變和壓應變后，介電峰均發生紅移。這一現象可由應變SiNWs能帶結構得到解釋，施加-10%壓應變和10%拉應變時，SiNWs帶隙均減小，帶隙變小導致電子在價帶和導帶間躍遷時所需的光子能量減小，因此介電峰均向低能區移動。

圖6 應變作用下摻雜SiNWs的介電函數虛部Fig.6 Imaginary part of dielectric function for the doping SiNWs under different strains

圖7 應變作用下摻雜硅納米線的吸收系數Fig.7 The absorption coefficient of the doping SiNWs under different strains

光學吸收系數反映了體系的光吸收能力，吸收系數α可以由復介電函數計算，計算公式為

(3)

圖7為不同應變時摻雜SiNWs吸收系數的變化曲線。SiNWs對光能量的吸收主要集中在0～7 eV，高于7 eV的范圍內吸收幾乎為零。10%拉應變、無應變和-10%壓應變時，吸收峰峰位分別出現在4.8、4.5、4.2 eV處。根據吸收光能量的范圍可知，空位摻雜及元素摻雜SiNWs對紫外光光輻射均有良好吸收，光吸收系數均在104cm-1以上，可以作為紫外光探測器優良替代材料。無應變作用下，相對于本征SiNWs，摻雜SiNWs的光吸收峰在低能區出現紅移現象，這與圖2中摻雜SiNWs最小禁帶寬度變窄的現象相吻合。去除Si原子的空位摻雜SiNWs光吸收帶寬有所增大，說明它對光能量的吸收范圍更寬，光電性能有所增強。而B原子的引入在紅外波段產生了新的吸收峰，說明B原子摻雜增強了電子在低能端的光學躍遷，提升了SiNWs在紅外光波段的光吸收特性。在低能區出現新的吸收峰，其源自價帶帶內電子躍遷。在10%拉應變作用下，可以看到吸收邊明顯紅移，吸收峰峰值和吸收帶寬明顯增大，因此吸收帶對低能區的紅外光、可見光和紫外光的光吸收均顯著增強。在可見光范圍內吸收系數隨著光子能量增加而增大，且吸收系數達到104cm-1，具有較高的光吸收系數，這符合太陽電池光吸收層的吸光要求，是優質的光伏材料。在-10%壓應變作用下，由于禁帶寬度顯著減小，電子從價帶激發到導帶上所需的能量更低，激發所需光源的波長變長，因此吸收光譜曲線與無應變時相比向低能方向移動。吸收邊紅移導致對可見光的吸收稍微增強，但整體的吸收帶寬和峰值均顯著減小，可以看到對紫外光的光吸收明顯減弱，同時紅外波段的吸收峰也消失。

折射率n和反射率R計算公式分別為

(4)

(5)

摻雜SiNWs的折射率與反射率在0～10 eV光子能量區域內的變化規律如圖8所示。在0～1 eV紅外區域內，元素摻雜SiNWs的折射率和反射率變化顯著，靜態折射率明顯增加，隨后折射能力迅速下降，反射能力增強，這段范圍內對紅外光的反射率最高達到88%。從圖8(a)不難看出，拉應變整體上提升了對紅外和可見光區域的折射能力，同時降低了對紫光區域的折射率，而壓應變基本呈現了相反的作用。從圖8(b)可以看出，在0～6 eV光子能量區域內，拉應變增加了摻雜SiNWs的反射率峰值，壓應變則降低了對紫外光的反射能力，同時增強了對可見光和紅外光的反射效率。

圖8 應變作用下摻雜硅納米線的折射率與反射率Fig.8 Refractive index and reflectivity of the doping SiNWs under different strains

3 結論

從密度泛函理論出發，在GGA近似下利用第一性原理方法研究了應變作用下空位摻雜與元素摻雜對SiNWs的電子能帶結構與光學特性的影響，得出以下結論。

(1)空位摻雜及元素摻雜會使SiNWs的導帶和價帶相對費米能級的位置發生顯著變化，同時能帶曲率也相應變化，而應變效應增強了這些變化。從微觀角度講，應變、空位摻雜與元素摻雜等因素對于光學特性的影響的本質歸因于它們對于能帶結構影響。

(2)相比于空位摻雜，元素摻雜更加明顯地改變了SiNWs的光學參數，尤其是摻雜B原子會顯著增強紅外區域的介電特性。單軸應變削弱了元素摻雜的影響，拉應變增強了SiNWs吸收帶寬和峰值，提升了光吸收的范圍和強度，尤其是可見光波段，使之成為優質光伏材料。壓應變則降低了對紫外光波段的吸收能力，但可見光波段的吸收稍有增加。

(3)元素摻雜顯著改變了紅外區域內SiNWs的折射率和反射率。拉應變提升了對紅外和可見光區域的折射能力，也顯著增加了摻雜SiNWs的反射率。壓應變則比較明顯地降低了對紫外光的反射能力，同時增強了對可見光和紅外光的反射效率。