考慮加工時間和交貨期模糊的批調度問題研究

王雷雷，趙永中，司佳佳，李小林

（中國礦業大學礦業工程學院，江蘇 徐州 221116）

1 引言

批處理機調度問題廣泛存在于半導體加工、鋼鐵的熱處理、港口貨物裝卸等生產場景中。不同于經典調度問題，批處理機可以將多個工件作為一批同時進行加工。其中，半導體加工的熱處理操作是典型的批處理機調度過程，該加工過程中，多個工件作為一批同時進行預燒處理以識別出早期失效的產品，根據產品的類型、質量等級等要求不同，預燒的時間甚至會長達120h，從而很容易成為瓶頸工序。

當產品可靠度水平要求不同時，其預燒時間通常會是一個區間值，同時隨著當前生產實際中顧客需求不確定性提高，產品的交期也經常出現大幅波動，因此對考慮模糊加工時間和交期的成批調度問題進行研究，并以滿意度為目標設計算法對問題進行求解。

對于單機環境下批處理機調度問題，文獻［1］首先對工件具有差異尺寸的預燒模型進行研究，證明該問題是強NP 難的。文獻［2］提出了一種改進的粒子群算法，解決了求最小化最大延遲懲罰的單機批調度問題。文獻［3］研究了相同交貨期的差異尺寸工件批調度問題，用精確算法對最小化工件總提前和延遲的目標進行求解。文獻［4］研究了目標為最小化工件最大延遲的單機批調度問題，提出了一種改進的粒子群優化算法。文獻［5］提出了蟻群-魚群混合算法來解決最小化工件制造跨度的目標。文獻［6］研究了在單批處理機上最小化工件完工時間的問題，提出了最大最小蟻群算法對該問題進行求解。

上述研究均是建立在時間參數確定的基礎上，但工件在實際加工過程中，由于工人和機器的不確定性，產品可靠性要求不同，加工信息不能準確預知，相關的時間參數是模糊的，進而具體交貨期也無法確定。隨著模糊調度理論在生產實際中的運用越來越廣泛，更多的學者開始投入到模糊環境批調度的研究中。文獻［7］考慮了模糊加工時間，建立了模糊完工時間模型，設計了蟻群算法，并采用特殊標準來選擇螞蟻的路徑。文獻［8］用梯形模糊數表示模糊交貨期，研究目標轉化為決策者對該工件完成時間具有的滿意度，并使用改進的帝國主義競爭算法（MICA）對問題進行求解。文獻［9］建立了模糊環境下的批容量問題、優先約束問題、交貨期問題和加工時間問題的一些單機批加工調度模型，并且給出了相應的求解算法。文獻［10］基于模糊加工時間和模糊交貨期建立了三種調度問題的模型，并采用遺傳算法搜索最優排序。文獻［11］同時考慮模糊加工時間和模糊交貨期，兩者均用三角模糊數表示，對于最小化工件的提前和延遲目標提出了一種混合的差分粒子群算法。文獻［12］研究了模糊環境下的并行批處理機問題，以最小化完工時間為優化目標，提出了模糊蟻群優化算法對問題進行求解。

現有研究大多考慮一種模糊量或者使用相同模糊數表示多個模糊量，而實際生產中，工件加工時間受加工特征及機器的影響與生產計劃所確定的顧客訂單交期通常具有不同的模糊數特征。因此，對工件加工時間與交貨期采用不同模糊數的批處理機調度問題進行研究，結合現有文獻中對加工時間和交期的模糊處理方式，分別采用三角模糊數和梯形模糊數表征工件的模糊加工時間和模糊交貨期。由于不同類型模糊數運算的差異，進一步將工件延遲轉化為完工時間相對于交期的滿意度，建立了工件模糊交貨期和模糊加工時間的隸屬度函數與決策滿意度的函數關系。在此基礎上提出模糊批調度數學模型，設計了改進帝國主義競爭算法對該問題進行求解，并通過仿真實驗對算法求解效果進行分析。

2 模糊環境下單機批調度問題

2.1 問題描述

模糊環境下單機批調度問題可描述如下：將n個工件的集合J={1 ，2，3，…，n} 安排在一臺批處理機M上加工，任一工件j具有差異化的尺寸sj。在滿足機器容量的條件下，可將多個工件分配至同一批進行加工。任一工件只分配至一個批中進行加工，批加工過程不允許中斷。

考慮實際生產中加工時間的不確定性，采用三角模糊數表示工件模糊加工時間，即工件j在批處理機上的加工時間為(pj1，pj2，pj3)，采用梯形模糊數表示工件模糊交貨期，任一工件j具有模糊交貨期晚于交貨期完工的工件j賦予一定的延遲懲罰βj。

工件j的加工時間隸屬函數，如圖1所示。

圖1 工件加工時間隸屬函數圖Fig.1 Membership Function Graph for Processing Time of Job

在模糊加工環境下，工件j的完工時間等于所屬批的模糊完工時間，任一批b的模糊完工時間由批工件的模糊加工時間取大得到，即批b的完工時間可由其所處位置k計算得到則工件完工時間隸屬度函數，如式（1）所示。

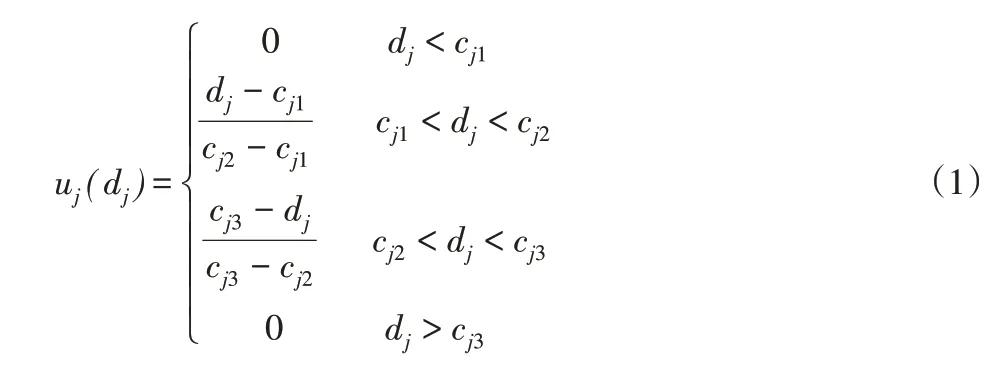
2.2 優化目標

當采用梯形模糊數表示模糊交期時，工件的最優交期會處于一個模糊區間，為了避免拖期，需要將工件盡量安排在模糊交期范圍內完成交貨。因此，批完工時間相對于交貨期梯形模糊數所處的位置即表達了顧客對于該完工時間的滿意程度。即顧客滿意度可根據交貨期梯形模糊數的后半部分與工件模糊完工時間運算取得。可用二元組（dj1，dj2）來表示完工時間相對于交期的滿意度，這里，dj1和dj2分別表示工件j交貨期模糊數的后兩個參數，即工件j按時交貨時間與拖后交貨時間。從而，工件j的交貨期隸屬函數可，如圖2所示。相應的隸屬度函數，如式（2）所示。

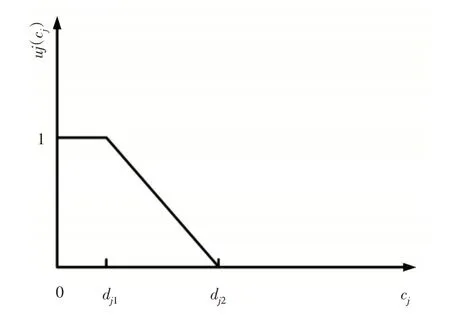
圖2 工件交貨期隸屬函數圖Fig.2 Membership Function Graph for Due Date of Job

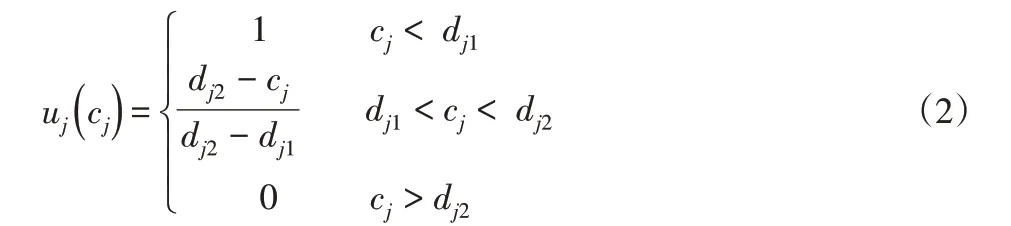
顯然，滿意度指數隨著交貨期隸屬度函數與完工時間隸屬度函數疊加區域的變化而變化，可能具有重疊區域，也可能無交集。當二者無重疊區域時S1=0 ，則滿意度指數AI=0 ；當二者重疊區域S1=S，則滿意度指數AI=1 ；否則重疊區域會出現如下三類部分重疊的情況，如圖3所示。

圖3 隸屬度函數重疊區域Fig.3 Membership Function Overlap Region

根據圖3中完工時間及交貨期隸屬函數重疊區域，可得三種情況下滿意度指數分別為：

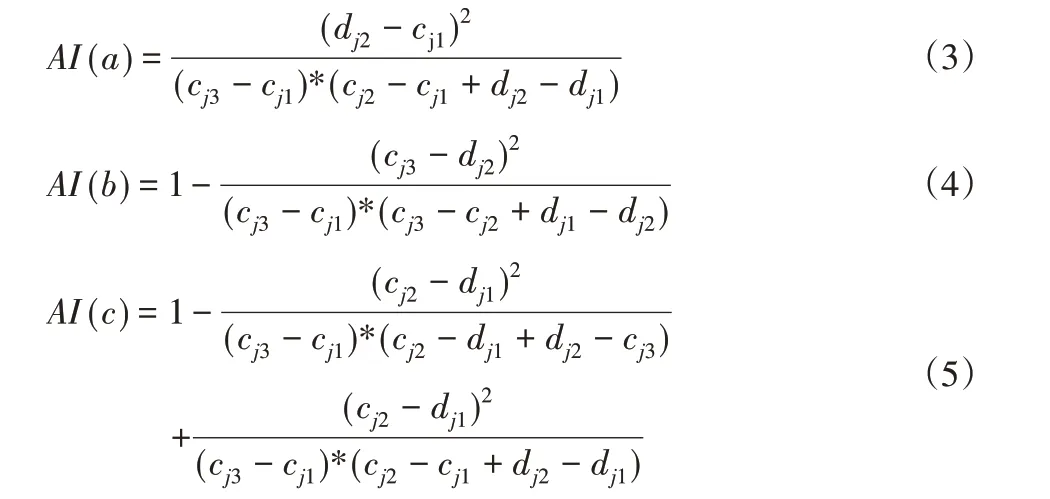
2.3 優化模型

問題所涉及參量說明如下：

cap：機器容量；sj：工件j尺寸；

SIj：工件j不滿意度指數，SIj=1-AIj；

βj：工件j延遲懲罰系數。

結合問題描述及滿意度定義，建立考慮模糊加工時間和交貨期的批調度問題數學優化模型如下：

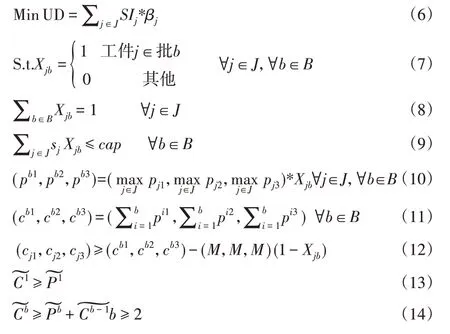
式（6）表示目標函數為最小化不滿意度UD，其中SI由上述不滿意度公式計算；約束（7）表示決策變量；約束（8）表示一個工件僅出現在一個批中；約束（9）表示任一個批的工件加工尺寸之和不得超過機器容量；約束（10）表示任一個批的模糊加工時間取決于對該批中所有工件進行模糊取大操作；約束（11）表示模糊批完工時間；約束（12）表示工件模糊完工時間與所在批相同；約束（13）和（14）確保每批的開始時間大于或等于其前一批的完成時間。

3 求解算法設計

帝國主義競爭算法（ICA）由文獻［13］首次提出，其基本思想來源于帝國主義殖民競爭機制。近年來帝國主義競爭算法的應用越來越廣泛，文獻［14］對帝國競爭算法進行了改進，解決了虛擬裝配過程中裝配序列規劃的問題。

ICA把種群比喻為世界，種群中的個體為國家，解的優越性與國家能力的大小具有一致性。一個帝國由一個宗主國組成，宗主國擁有多個殖民地。殖民地受所屬宗主國以及其他帝國中的宗主國和殖民地的影響，會發生移動。當殖民地的成本低于其宗主國成本時，兩者位置互換，然后帝國之間競爭吞并。在下一次競爭中，強者獲勝，循環往復直至最后，世界只剩下一個帝國，完成算法搜索。

3.1 帝國集團編碼與初始化

在帝國主義算法中，每個解稱為一個國家，對于n個工件的成批調度問題，每一個解可以表示成一個n維的向量，Ki=(k1，k2，k3，...，kn)，即表示第i個國家，向量中的每個分量為該位置的工件編號，采用隨機鍵（Random Key）編碼的方式隨機生成工件序列集合作為初始國家集合。

3.2 國家成本函數計算

為了直觀的評判一個國家勢力的強弱，用成本函數作為標準：Ci=f(Ki)。成本函數與國家勢力成反比。成本函數用于計算給定問題的目標函數，對應不滿意度。

對于任一工件序列，設計BFEDD分批規則來求解每個國家的成本函數如下：

算法BFEDD（Best Fit Earliest Due Date）：

（1）選擇工件序列首部第一個工件，將其放入到當前可以容納它且該批次剩余容量為最小的批中。如果所有工件分配完畢，轉（3）；

（2）若現有批次均無法容納該工件，創建新批，轉（1）。

（3）將批列表按交期非減排序，并順序安排至機器，得出任一批的完工時間。

（4）結合2.2節中各AI計算公式，計算任一工件滿意度指數，以及總體不滿意度指數，即為成本函數。

假設所有國家數為N，其中有Nimp個國家由于勢力強大成為宗主國，則剩下的Ncol個國家成為殖民地，且N=Nimp+Ncol。殖民地按一定的比例分配給宗主國，Nimp個宗主國獲取相應的殖民地后，則建立了Nimp個帝國。

3.3 帝國同化殖民地策略改進

同化政策發生在每個帝國內部，是殖民地向宗主國不斷靠近的過程，具體是指沿著宗主國和該殖民地間連線隨機移動一個距離x，其中，x必須滿足均勻分布：x～U(0，α*d)，α為大于1的數，通常取α=2。為了增加算法的搜索廣度，賦予一個隨機角度偏移量θ，且θ滿足均勻分布：θ～(-γ，γ)，通常情況下γ=π/4。

為了避免在同化過程中搜索方向單一，即殖民地只受所屬宗主國的影響的情況，這里考慮殖民地同時受所屬宗主國和帝國中的其他殖民地以及其他帝國中的宗主國的影響。同時，國家之間的“距離”越小，產生的影響越大。為了提高算法的全局搜索能力，同時考慮不同國家之間距離的非線性影響，國家之間的吸引力計算設計如下。

用OFi表示目標函數，wi代表國家勢力，di代表兩個國家間的距離。其他宗主國對該殖民地的吸引力為γi，殖民地對殖民地的吸引力為η。

當國家1受到超過三個國家的影響時，此時國家1移動后的情況如式（16）。

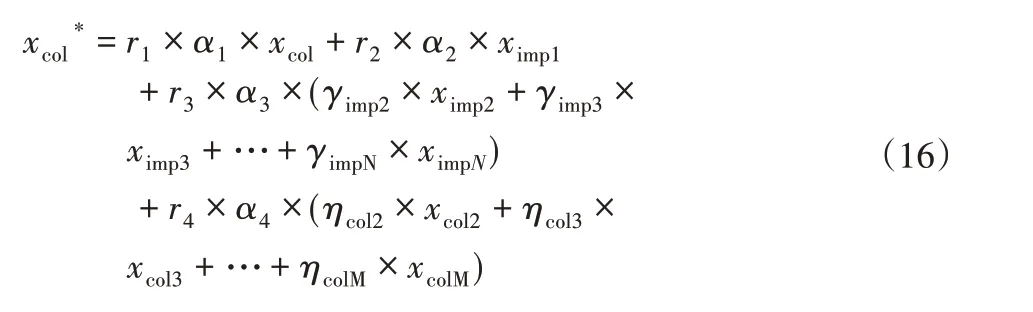
式中：α1—國家1維持原狀的可能性；αi(i=2，3，4)—國家1向各個國家移動的概率，0 ≤αi≤1，—當事國的現狀；ximp1—所屬宗主國的現狀；ximp2+ximp3+...+ximpN—相鄰宗主國的現狀；xcol2+xcol3+...+xcolM—同一帝國中，其他殖民地的近況，隨機數ri(i=1，2，3，4)∈[ 0，1 ]。

當殖民地在多方國家影響下到達一個新位置時，在新位置上的勢力可能比其宗主國的勢力更大，其成本也更低。此時，就將該殖民地和宗主國的位置互換。

3.4 改進的帝國主義競爭算法

改進的帝國主義競爭算法（IICA）步驟如下：

（1）根據帝國集團編碼方法，生成N個國家，完成國家初始化。

（2）根據國家成本函數計算方法，對帝國集團任一國家Ki計算其當前的成本函數。確定了Nimp個帝國后，每個帝國中的宗主國對應的成本函數做為當前帝國的最優解。

（3）根據同化策略改進方法，計算每個帝國中殖民地同化后的成本函數，若小于其宗主國的成本，則將當前最優解更新。帝國之間進行競爭，計算每個帝國的總成本，勢力大的帝國吞并勢力小的帝國中的國家，消除最弱帝國。

（4）判斷算法終止條件（達到最大迭代次數Nmax或最終剩下一個帝國），若滿足終止條件，則輸出最終的調度方案及不滿意度，否則轉（3）。

4 仿真實驗

4.1 參數選取

這里采用隨機方法產生算例，算例的規模包括工件個數（n），工件的加工時間工件尺寸和工件交貨期。pj2大小服從均勻分布，分別在［1，10］和［1，20］隨機產生。設機器的容量cap為10。工件尺寸sj分別從均勻分布［1，10］、［2，4］和［4，8］中產生。因此，算例類別共計10×2×3=60 類。具體的參數和水平，如表1所示。

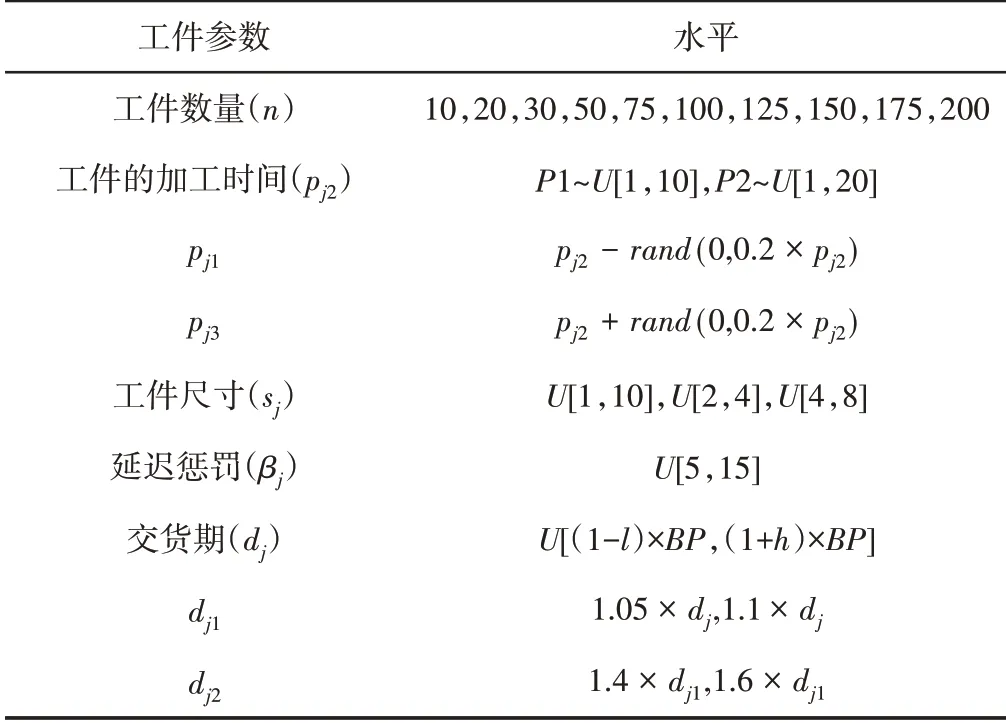
表1 實驗數據的工件參數Tab.1 Various Parameters of Experimental Data

其中，交貨期的產生方式如下，確定單個工件平均模擬加工時間和平均模擬批數，由此獲得總模擬加工時間BP。

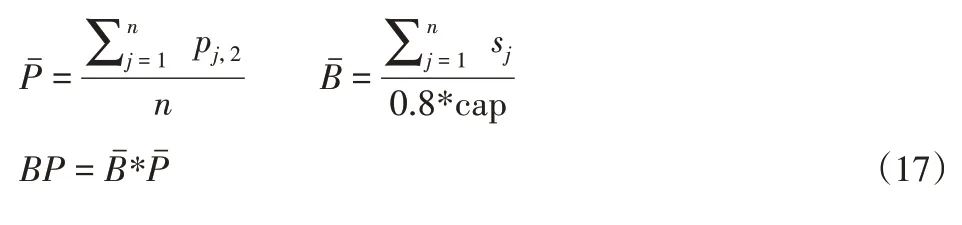
交貨期參數dj由以下均勻分布產生：

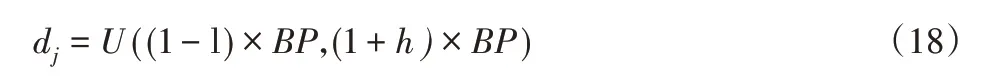
式中：l和h—下限和上限，分別設置為0.1和0.7。

4.2 實驗結果及分析

在本節中，將IICA 算法的結果與原始ICA 和文獻［8］提出的MICA 算法進行比較。IICA 算法中設置國家規模為1.5n，Nimp的比例為0.15，α1，α2，α3，α4分別為0.25，0.125，0.125，0.5。對每類算例生成10個實例，以平均值進行比較。按照加工時間不同，將工件尺寸分別為［1，10］，［2，4］［4，8］求得的結果取均值。由于目標函數是最小化UD，定義任一算法A相對于所提IICA算法差距公式Gap（A）%如下。

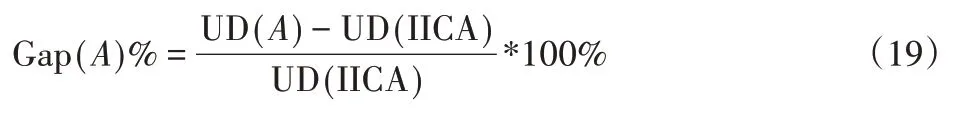
式中：UD（A）—算法A所求的目標函數UD值。

由表2可看出，IICA 算法總體上優于MICA 算法，平均幅度達到3.2%，IICA算法優于ICA 算法的幅度平均達到7.5%。將表2獲得的ICA、MICA和IICA的結果按照加工時間不同做比較，P1和P2時間下的分類顯示，如圖4、圖5所示。

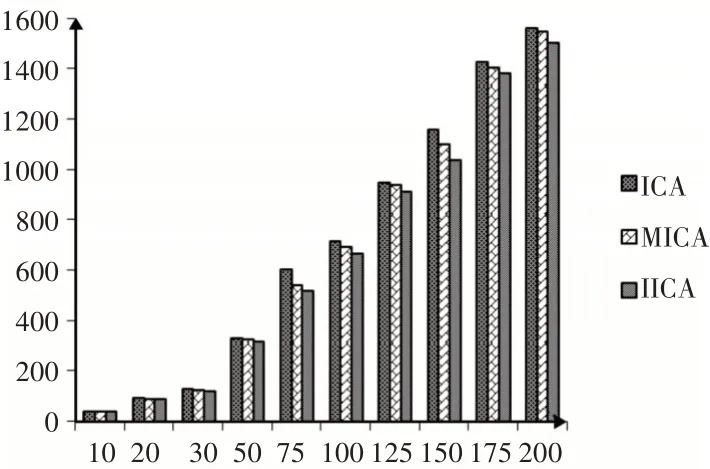
圖4 P1類中每個算法的結果Fig.4 The Result of Each Algorithm in Class P1

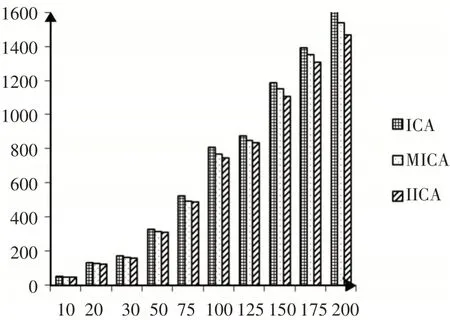
圖5 P2類中每個算法的結果Fig.5 The Result of Each Algorithm in Class P2

工件的總不滿意度隨著工件規模越大呈現上升趨勢，當工件規模較小時，無論是P1類還是P2類，ICA、MICA和IICA獲得的最終結果差別不大，但隨著工件規模的增加差別越來越明顯，ICA的優化效果最差，IICA的優化效果要優于ICA和MICA。

為了進一步比較算法的性能，這里設計了統計分析實驗對算法進行統計檢驗。首先將實驗輸出結果數據進行正態性檢驗得出數據符合正態分布，隨后利用方差分析（ANOVA）模型進行檢驗。

模型顯示為：

式中：μ—整體平均值；

τi(i=1，2，3)—3種不同算法的效果；

βj(j=1，2...60)—第j個樣本的實例效果；

εij—隨機誤差。

采用95%的置信度進行檢驗，檢驗結果，如表3所示。基于P值對三種算法進行比較，可認為置信度檢驗是可靠的。為了比較各算法之間的性能排序，選用Least Significant Difference（LSD）進行檢驗結果，如表4所示。

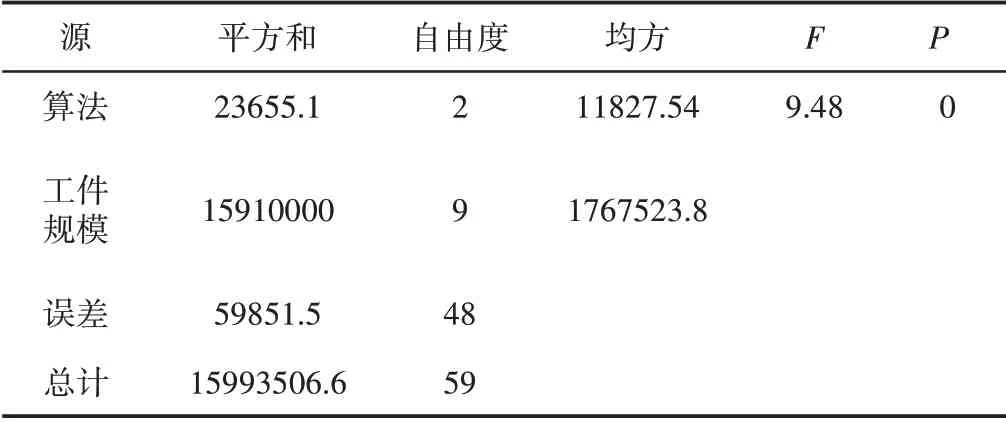
表3 算法的ANOVA結果Tab.3 ANOVA Results of Algorithm

根據LSD測試的結果，可知三種算法的性能之間存在顯著差異。通過分析可以得出，IICA具有最佳性能。這表明，改進后的殖民地移動策略提高了ICA的性能，同時，嵌入有效地啟發式規則，能夠有效地提升搜索解空間的效率。

5 結論

對加工時間和交貨期模糊的成批調度問題進行了研究，將確定型環境下的工件總延遲目標轉化為模糊制造系統中的不滿意度，構建了問題的模糊數學模型。針對帝國主義算法容易陷入局部最優的問題，改進殖民地的移動策略，結合批調度的啟發式規則設計IICA算法對問題進行求解。設計仿真實驗對IICA的有效性進行分析，IICA算法在各類算例平均優于MICA和ICA算法的幅度分別為3.2%和7.5%。這里所研究問題可擴展到考慮工件到達時間的不確定性以及多機環境等情況，對于模糊環境下工件準時交貨的目標也可進一步研究。