RV傳動壓力角的影響因素及變化規律研究

徐宏海，李旭光

（北方工業大學機械與材料工程學院，北京100144）

1 引言

RV減速器是由輸入級行星齒輪傳動和輸出級行星擺線針輪傳動組成的兩級傳動機構，采用中心圓盤支承結構，具有傳動比大、體積小、剛度大、承載能力大、傳動精度和傳動效率高等優點，廣泛應用于工業機器人關節驅動和數控機床傳動裝置中［1-5］。

RV 減速器屬多齒嚙合傳動，理論上有一半的齒參與嚙合。擺線輪是RV減速器的關鍵零件，其齒廓一般為短幅外擺線的等距線。擺線輪齒廓上同時參與嚙合的點的壓力角是變化的，壓力角的大小影響傳力性能，過大的壓力角會導致非常大的徑向力，從而影響RV減速器的使用壽命。

文獻［6］從擺線方程入手，研究分析齒廓參數對單齒嚙合壓力角的影響，未考慮齒廓修形參數影響及多齒嚙合平均壓力角的變化規律。文獻［7］應用齒輪嚙合原理，建立擺線輪齒廓方程和單齒嚙合壓力角、多齒嚙合平均壓力角方程，仿真分析了設計參數對壓力角的影響規律，但未體現同時參與嚙合齒號的動態變化情況，也未考慮擺線輪齒廓修形參數的影響。

這里根據擺線輪與針輪的相對運動關系，導出擺線輪齒廓方程、單齒嚙合壓力角和多齒嚙合平均壓力角的計算公式，運用Matlab編程，仿真分析同時參與嚙合齒號的變化規律及設計參數和修形參數對壓力角的影響規律。

2 擺線輪標準齒廓方程

與標準針輪嚙合、與針齒共軛且無嚙合間隙的擺線輪齒廓稱標準齒廓。選擇擺線輪幾何中心Oa為原點，與擺線輪齒槽對稱軸重合的軸線為y軸，如圖1所示，Ob為針輪幾何中心。假設擺線輪固定不動，考慮RV 減速器最普遍使用的正一齒差傳動情況（Zb－Za=1，Zb為針輪齒數，Za為擺線輪齒數），針齒初始位置與y軸重合，當針輪繞Ob自轉θ時，針輪繞Oa公轉（平動）的角度為Zbθ，則擺線輪的標準齒廓方程如下：

圖1 擺線輪齒廓曲線Fig.1 Cycloid Gear Tooth Profile Curve

式中：RZ—針齒中心分布圓半徑，mm；e—偏心距，mm；rZ—針齒半徑，mm；K—短幅系數，K=eZb/Rz；β—嚙合點公法線與x軸的夾角，Rad。

3 傳動壓力角

RV傳動屬多齒嚙合行星傳動，如圖2所示。針輪繞Oa順時針公轉可看作是針輪固定、轉臂逆時針轉動，故擺線輪順時針自轉。n為嚙合點A的法向矢量，τ為擺線輪齒廓上A點的切向矢量（τ⊥n），v為嚙合點A擺線輪自轉速度矢量，α為嚙合點A的壓力角，φ為OaA與x軸的夾角（傾角），AB∥x軸。

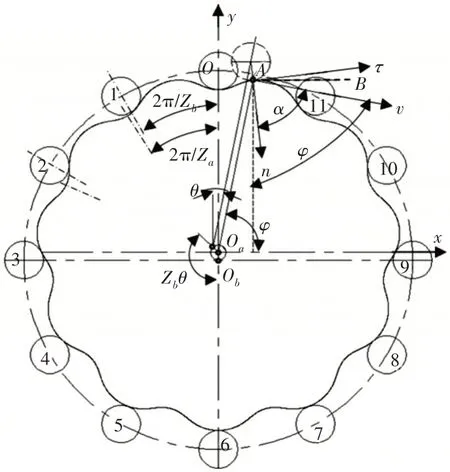
圖2 RV傳動嚙合原理Fig.2 Engagement Theory of RV Transmission

根據圖2及擺線輪齒廓方程可求得0號針齒在嚙合點A（x，y）位置時的壓力角為［8］：

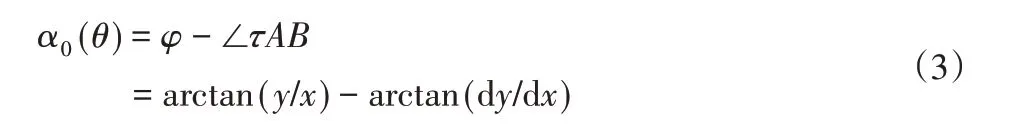
如圖2所示，擺線輪與針輪同時有多個嚙合點，針輪順時針轉動時，y軸右側針齒與擺線輪之間有分離趨勢而沒有作用力存在，y軸左側針齒與擺線輪之間相嚙合傳動而存在作用力與反作用力，因此理論上同時嚙合齒數為針齒數的一半（圖示位置為針齒號0，1，2，3，4，5，是動態變化的）。對于兩擺線輪位置相差180°布置的RV減速器，為滿足擺線輪齒高等于2倍偏心距的安裝要求（一個擺線輪的齒根與針齒嚙合時，另一個擺線輪的齒頂與針齒嚙合），擺線輪的齒數必須為奇數［9］。因此對于一齒差傳動，針輪齒數為偶數，同時嚙合齒數為整數。各針齒與擺線輪嚙合點相對于擺線輪齒根的初始位置是不同的，針齒（ii=1，2，...）與擺線輪的嚙合點初始位置與0號針齒相比，針輪多自轉了一個初始角度（2π/Za－2π/Zb）i，即針齒i嚙合點的壓力角等于0號針齒轉過（2π/Za－2π/Zb）i時的壓力角。若0號針齒的θ角為θ（0），則第i個針齒對應的θ角為：

將式（4）代入式（3）得到第i個針齒與擺線輪嚙合點的壓力角α（iθ（i））。

各嚙合點壓力角的平均值為：

由于傳動壓力角是力與速度方向所夾的銳角即α≤90°，因此按上述方法計算的壓力角α（iθ（i））>90°時，則不予統計（實際上此時針齒i不傳遞力）。

4 單齒嚙合壓力角的影響因素及規律

4.1 單齒嚙合壓力角

以圖2中0號齒為例，嚙合點從擺線輪齒根-齒頂-齒根的過程為一個嚙合周期。一個嚙合周期對應的角度θ=360°/Za，各參數值：Rz=150mm，rz=15mm，e=8.75mm，Zb=12，Za=11。運用matlab編程得到0號齒一個嚙合周期內的壓力角變化規律，如圖3所示。0號齒從齒根到齒頂嚙合過程中的壓力角先減小后增大，且壓力角減小的速率大于增大的速率，在齒根和齒頂處壓力角α=90°，N點處壓力角最小α=43.6834°；后半周即齒頂-齒根嚙合過程的壓力角大于90°（不傳遞動力），不納入分析。

圖3 單齒嚙合壓力角變化規律Fig.3 Variation of Single Tooth Meshing Pressure Angle

4.2 設計參數對單齒嚙合壓力角的影響

由式（1）～式（5）可知影響壓力角的主要參數有：Rz、rz、e。運用MATLAB編程進行仿真分析，得到0號齒一個嚙合周期內各參數對壓力角的影響規律，如圖4～圖6所示。

由圖4～圖6可知：隨著偏心距e的增大和針齒分布圓半徑Rz的減小，單齒嚙合壓力角減小，壓力角最小值位置向齒根靠近，壓力角變化速率及幅度加劇；由于短幅系數K=eZb/Rz，因此可歸結為單齒嚙合壓力角隨短幅系數的增大而減小。針齒半徑rz對單齒嚙合壓力角的影響很小，可以忽略不計。

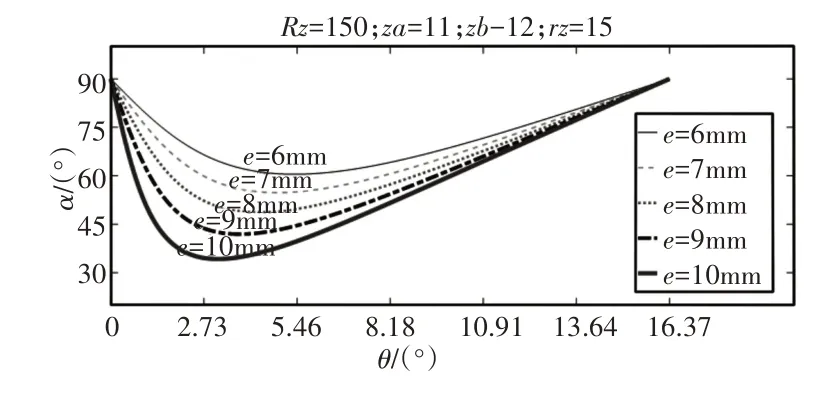
圖4 偏心距e對單齒嚙合壓力角的影響Fig.4 Effect of Eccentricity on Pressure Angle for Single Tooth Meshing

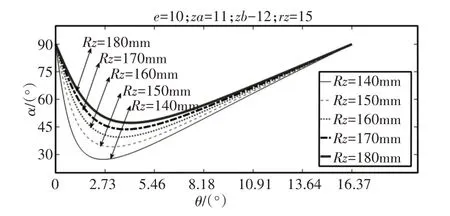
圖5 針齒分布圓半徑Rz對單齒嚙合壓力角的影響Fig.5 Effect of Needle Tooth Distribution Circle Radius on Pressure Angle for Single Tooth Meshing

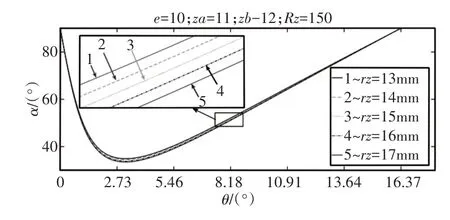
圖6 針齒半徑rz對單齒嚙合壓力角的影響Fig.6 Effect of Needle Tooth Radius on Pressure Angle for Single Tooth Meshing

5 多齒嚙合平均壓力角的影響因素及規律

5.1 多齒同時嚙合壓力角變化分析

以圖3相同設計參數為例，運用MATLAB編程和仿真，得到一個嚙合周期內多齒同時嚙合壓力角的變化規律圖，如圖7所示。

圖7 多齒同時嚙合壓力角變化規律Fig.7 Variation of Pressure Angle of Multiple Teeth Simultaneous Meshing

由圖7可知：一個嚙合周期內，在任意θ位置處，同時嚙合齒數為6（等于Zb/2），從圖2所示初始位置開始，同時嚙合針齒號依次為0～5、11和0～4、10～11和0～3、9～11和0～2、8～11和0～1、7～11和0、6～11、5～10、4～9、3～8、2～7、1～6，接著開始下一個循環。不同針齒參與嚙合時的壓力角變化規律、周期與0號針齒一樣，但初相位與0號針齒相差（2π/Za－2π/Zb）i，（i=1，2，...，11）。

一個嚙合周期內的多齒嚙合平均壓力角變化規律，如圖8所示。平均壓力角呈周期性變化，一個周期對應的角度θ=360°/（Za×Zb）。

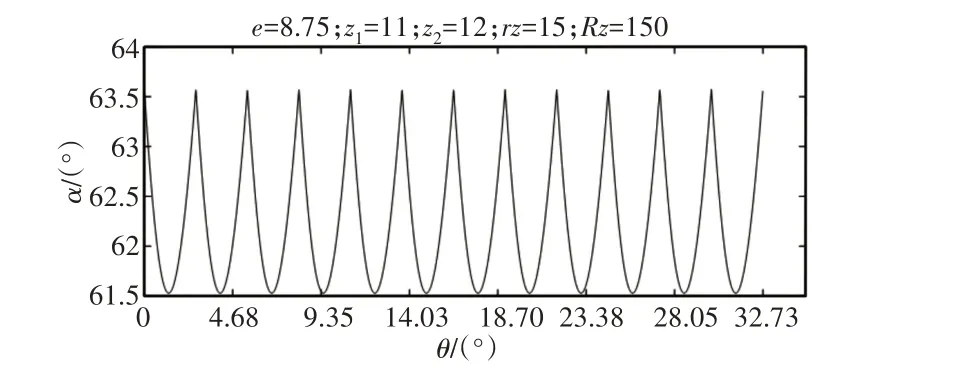
圖8 多齒嚙合平均壓力角變化規律Fig.8 Variation of Average Pressure Angle of Multiple Teeth Meshing

5.2 設計參數對多齒嚙合平均壓力角的影響

Rz、rz、e對多齒嚙合平均壓力角的影響，如圖9～圖11所示。

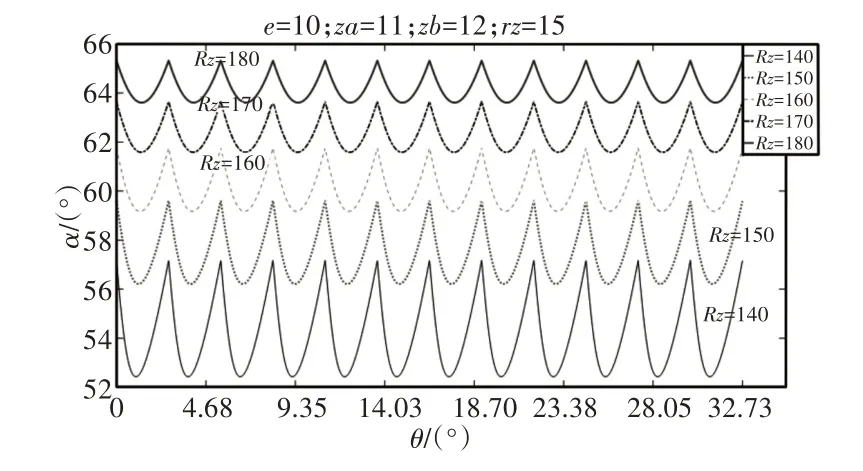
圖9 針齒分布圓半徑Rz對多齒嚙合平均壓力角的影響Fig.9 Effect of Needle Tooth Distribution Circle Radius on Average Pressure Angle for Multiple Teeth Meshing

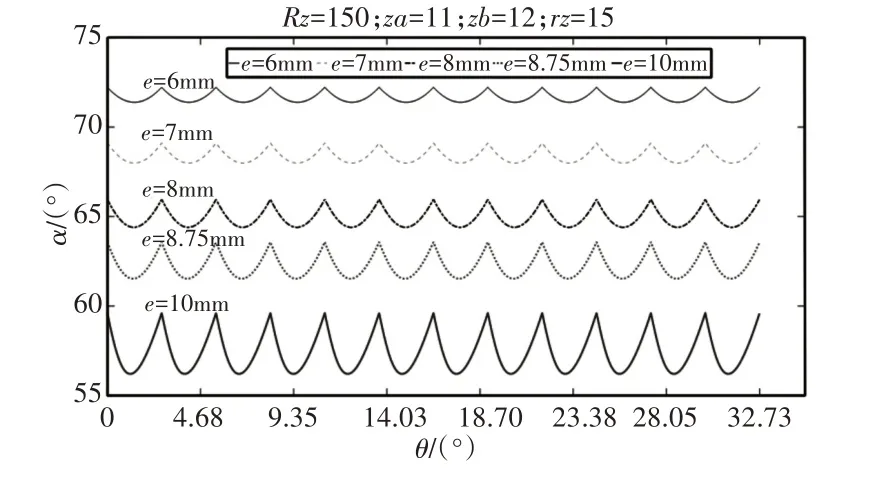
圖10 偏心距e對多齒嚙合平均壓力角的影響Fig.10 Effect of Eccentricity on Average Pressure Angle For Multiple Teeth Meshing

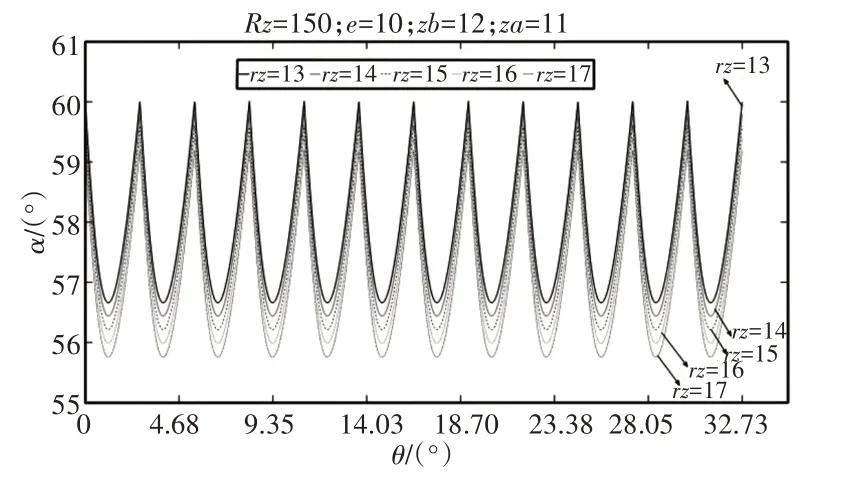
圖11 針輪半徑rz對多齒嚙合平均壓力角的影響Fig.11 Effect of Needle Tooth Radius on Average Pressure Angle for Multiple Teeth Meshing

由圖9～圖11 可知：多齒嚙合平均壓力角隨Rz的減小而減小、隨e的增大而減小，即隨短幅系數的增大而減小；隨著rz的增大，平均壓力角略有減小；平均壓力角變化幅值隨Rz的增大而減小、隨e的增大而增大。隨rz的增大，平均壓力角變化幅值略有增加；當θ=i×360°（/Za×Zb），i=0，1，2，…時平均壓力角最大，θ=i×360°（/Za×Zb×2），i=1，2，3，…時平均壓力角最小。

6 齒廓修形對傳動壓力角的影響

6.1 考慮修形參數的擺線輪齒廓方程

擺線輪通常采用以下三種修形方式［10］：

（1）等距修形。在修磨擺線輪時，將磨輪半徑rz增加（正等距）或減少（負等距）△rz，磨出的擺線輪齒廓是標準齒廓的法向等距曲線。（2）移距修形。修磨擺線輪時，使磨輪與擺線輪間的中心距（即R）z增加（負移距）或減少（正移距）△Rz。（3）轉角修形。修磨擺線輪時，磨輪中心相對于擺線輪中心偏轉△θ角。

根據擺線輪齒廓成形及修形方式原理，結合式（1）～式（2）得到考慮修形參數時的擺線輪齒廓方程：

6.2 修形參數對傳動壓力角的影響

運用MATLAB編程，仿真分析移距修形量△Rz、等距修形量△rz、轉角修形量△θ對單齒嚙合壓力角的影響，如圖12～圖14所示。

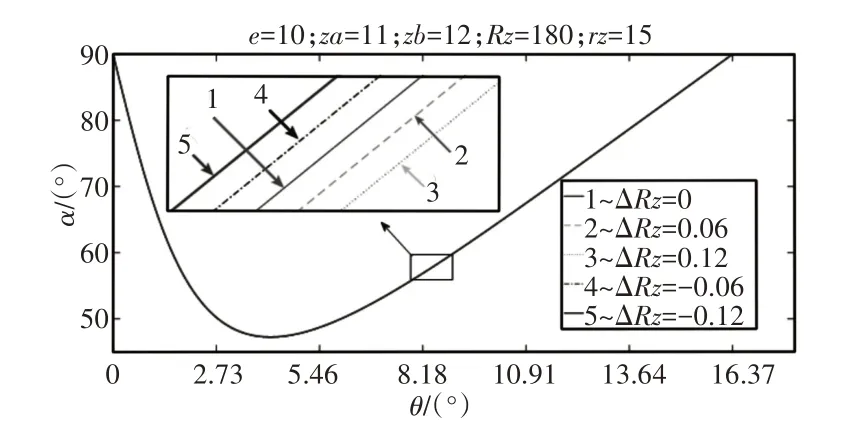
圖12 移距修形量△Rz對單齒嚙合壓力角的影響Fig.12 Effect of Displacement Modification on Pressure Angle for Single Tooth Meshing

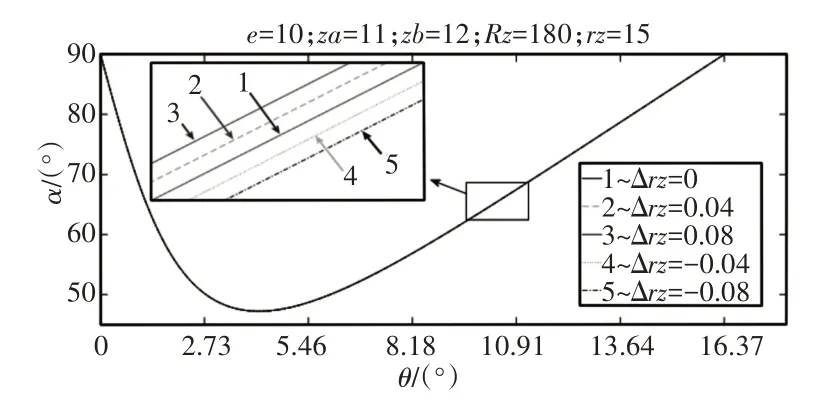
圖13 等距修形量△rz對單齒嚙合壓力角的影響Fig.13 Effect of Iisometric Shape Modification on Pressure Angle for Single Tooth Meshing

圖14 轉角修形量△θ對單齒嚙合壓力角的影響Fig.14 Effect of Angle Modification on Pressure Angle for Single Tooth Meshing

由圖12～圖14可知：移距修形和等距修形對壓力角的影響都甚微，壓力角隨正移距修形量和正等距修形量的增大而略微減小，隨負移距修形量及負等距修形量的增大而略微增大，齒根和齒頂處的壓力角不變，仍為90°。轉角修形對壓力角無影響。擺線輪齒廓修形對壓力角的影響可以忽略不計，修形的主要目的在于產生形成油膜所需的嚙合間隙，改善潤滑狀況。

7 結論

（1）RV傳動的壓力角呈周期性變化，一個嚙合周期對應的針輪自轉角度θ=360°/Za。一個嚙合周期內，單齒嚙合壓力角變化一次，多齒嚙合平均壓力角變化Zb次。

（2）增大偏心距、減小針齒分布圓半徑、增大針齒半徑，均可使壓力角減小。壓力角變化幅值隨Rz的增大而減小，隨e的增大而增大，隨rz的增大略有增加。偏心距對壓力角的影響最大，針齒分布圓半徑其次，針齒半徑影響最小。因此在設計擺線輪機構各參數時，應主要考慮偏心距、針齒分布圓半徑兩個因素（即短幅系數）的影響。

（3）RV傳動同時嚙合齒數為針齒數的一半，在傳動過程中，不同針齒依次輪換，參與嚙合傳力。從針輪轉動方向看，當嚙合點位于擺線輪齒廓的齒根-齒頂之間時，針齒與擺線輪之間存在嚙合力；當嚙合點位于擺線輪齒廓的齒頂-齒根之間時，針齒與擺線輪之間無嚙合力。

（4）移距修形和等距修形對壓力角的影響很小，轉角修形對壓力角無影響。