一種防御體系抗毀傷度量方法研究*
張永健,康鵬,卓志敏,鄭大國
(北京電子工程總體研究所,北京 100854)
0 引言
面對空襲體系與防御體系日益激烈的對抗,無論是指揮控制節點、通信節點,還是制導雷達、發射平臺,都不能完全避免被毀傷的可能。傳統基于核心節點構建的樹狀防御體系架構已經難以適應現階段高強度的體系作戰,其核心節點的失效將直接導致獨立的防御系統喪失防御能力,體系抗毀性能較差[1-4]。而分布式防御體系通過作戰設備節點高度備份的能力,使體系在強對抗環境及部分節點或單元癱瘓、損毀的情況下仍能保障大部分防御作戰能力。
目前,防御體系抗毀傷的度量方法大多是針對于設備節點自身抗毀傷能力進行研究的,針對整個防御體系結構進行抗毀傷度量的方法還較少[5-6]。鑒于防御裝備體系分布式改造成為重點發展方向,研究一種綜合體系結構與設備節點生存能力的防御體系抗毀傷度量方法,具有重要的現實意義。
1 防御體系結構分析
防御體系的結構主要反映防御體系組成要素以及要素之間的相互關系。
1.1 防御體系組成要素
雖然防御體系按結構的不同可以劃分為傳統平臺化中心化防御體系和網絡中心化防御體系,但不同結構的防御體系開展防御作戰的流程基本是相同的,其打擊鏈路的組成都可以分為“偵察—控制—打擊”3個主要環節。每個環節都包含一定數目的設備節點,當3個環節內都存在工作正常的設備節點且滿足構成打擊鏈路的通信條件時,防御體系才能對目標進行打擊。
1.2 樹狀防御體系結構
傳統樹狀防御體系中包含多個獨立武器系統,這些系統中包含一個偵察節點、一個控制節點以及若干個打擊節點,其通信結構是基于核心節點構建的樹狀結構,這種結構具有成本低、通信線路總長短、軟件簡單、體系易于實現等優點。但同時這種結構也存在著許多嚴重的不足。傳統防御體系的抗毀性、可靠性存在較大的問題,一旦核心節點或與核心節點相連的線路受毀失效,會使體系癱瘓而喪失基本的防御能力;其戰場資源的隸屬關系過于明確,打擊鏈路各個環節之間構成嚴格的耦合關系,不能分拆;作戰資源的指揮和信息下達必須自上而下逐級傳遞,發射打擊平臺之間的信息交流必須通過上一級作戰單元進行傳遞,由此導致信息鏈路過長,容易延誤戰機[7-9]。
1.3 分布式防御體系結構
分布式防御體系內部的組成要素與傳統的防御體系基本是相同的,但要素之間的連接方式與傳統的防御體系有著很大的不同。分布式防御采用一種網狀的體系結構,這種結構顛覆了傳統防御體系樹狀的架構和彈站架高度耦合的作戰使用模式,在所有設備之間構建了多種通信鏈路,使得所有設備間可以共享信息,實現網內資源的共享,這大大提高了體系的抗毀生存能力[10-11]。例如,在面臨強對抗環境以及部分節點或單元癱瘓、損毀的情況下,分布式防御體系能通過設備間的資源共享,重組受損的打擊鏈路,以保障核心作戰任務的完成,這體現了體系架構在攻擊行為或不利環境下保持任務成功執行的能力。分布式防御體系是依靠網絡中心化的發展而發展的,在網絡中心化的作用下,使防御體系有機地集成為“形散而神不散”的整體,充分發揮了體系的作戰效能[12-15]。
2 防御體系抗毀傷度量方法研究
以往防御體系抗毀傷能力的度量方法一般側重于設備節點本身,而沒有考慮體系結構的影響,其度量的結果主要反映的是防御體系內部節點在作戰過程中不被發現、發現后不被命中、命中后不易毀傷的能力,不能有效說明不同結構防御體系給抗毀能力帶來的改變[2]。為了更全面、更準確地對防御體系的抗毀傷能力進行度量,需綜合分析體系結構及體系內部節點的生存能力。
防御體系抗毀性是指在體系面臨敵襲損傷或自身節點失效的情況下,體系維持或恢復其防御性能到一個可接受程度的能力。從打擊空襲目標的角度上看,防御體系是否具備防御性能可以用防御體系組織打擊鏈路的能力來進行衡量,如果體系不能有效組織打擊鏈路,可視為該體系不具備體系作戰能力,即防御體系受毀失效。在攻防對抗場景下,防御體系內部設備節點都有“正常工作”和“損傷癱瘓”2種可能的狀態。若防御體系內部有設備節點總數為x,則整個防御體系可能的工作狀態就有2x種。綜合上述分析,防御體系的抗毀傷能力可用體系在所有可能工作狀態下組織打擊鏈路條數的期望值E來進行度量,期望值越大則說明防御體系的抗毀傷能力越好。
防御體系內某一打擊節點能組成完整打擊鏈路需要滿足3個條件:一是這個打擊節點處于正常工作狀態;二是與這個打擊節點存在通信關系的偵察節點處于正常工作狀態;三是與這個打擊節點存在通信關系的控制節點處于正常工作狀態。若防御體系內打擊節點的總數為N,則防御體系最多能同時利用這N個打擊節點組成N條打擊鏈路,故防御體系能同時組織打擊鏈路條數的期望值E可通過式(1)進行計算。
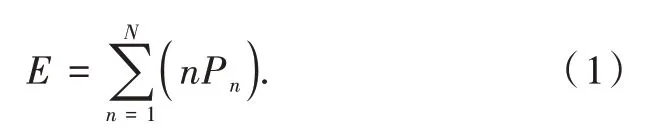
式中:N為體系最多能同時構建打擊鏈路條數,其數值與打擊節點總數相同;Pn為體系最多能同時構建n條打擊鏈路的概率。
2.1 針對傳統樹狀防御體系的度量方法
傳統樹狀防御體系由多個獨立系統構成,每個獨立系統中包含有一個偵察節點、一個控制節點以及若干個打擊節點。用Di表示獨立系統i內的打擊節點集合,則整個防御體系的打擊節點集合D滿足

因為集合D中有N個打擊節點,所以其包含n個打擊節點的子集個數為CnN,用Snm表示集合D包含n個打擊節點的子集,其中m=1,2,…,CnN表示子集的編號。防御體系最多能同時構建n條打擊鏈路說明體系內有且僅有n個打擊節點滿足構建完整打擊鏈路的3個條件,用Pnm表示事件“防御體系有且僅有Snm中n個打擊節點滿足構建打擊鏈路的3個條件”發生的概率,故有

用Pnmi表示事件“獨立系統i中有且僅有Snm∩Di中打擊節點滿足構建打擊鏈路3個條件”發生的概率。因為傳統防御體系是由多個獨立系統組合而成的,故有
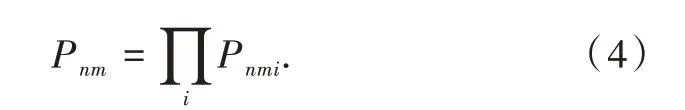
對于Pnmi的計算可分為2種情況:一種情況是Snm∩Di=?,此時獨立系統i中的所有打擊節點都不滿足構成打擊鏈路的3個條件,即獨立系統i無法構建打擊鏈路;另一種情況是Snm∩Di≠?,此時獨立系統i中存在打擊節點滿足構成打擊鏈路的3個條件,即獨立系統i可以構建打擊鏈路。Pnmi可表示為

式中:PSi為獨立系統i內偵察節點的生存概率;PCi為獨立系統i內控制節點的生存概率;PAij為獨立系統i內打擊節點j的生存概率。
綜合上述的分析,傳統防御體系能同時組織打擊鏈路條數的期望值E為

2.2 針對分布式防御體系的度量方法
分布式防御體系通過組網通信的手段將戰場中所有設備節點互聯互通,防御體系內所有節點不再隸屬于某個獨立系統。同樣用D表示防御體系內所有打擊節點構成的集合,用Snm表示集合D包含n個元素的子集,其中m=1,2,…,CnN表示子集的編號。用Pnm表示事件“防御體系有且僅有Snm中n個打擊節點滿足構建打擊鏈路的3個條件”發生的概率,同樣有

在分布式防御體系中,對Pnm計算如下
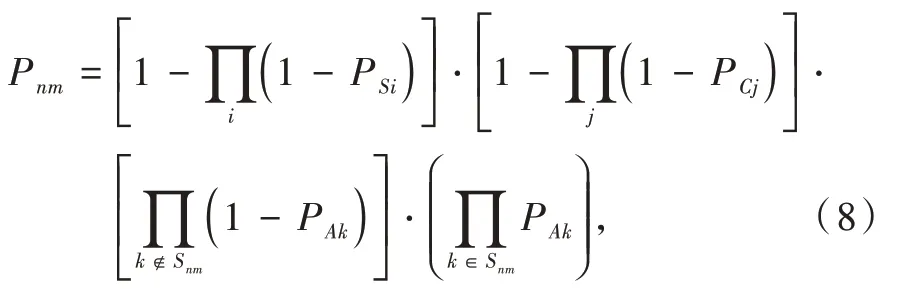
式中:PSi為防御體系內偵察節點i的生存概率;PCj為防御體系內控制節點j的生存概率;PAk為防御體系內打擊節點k的生存概率。
綜合上述的分析,分布式防御體系能同時組織打擊鏈路條數的期望值E為
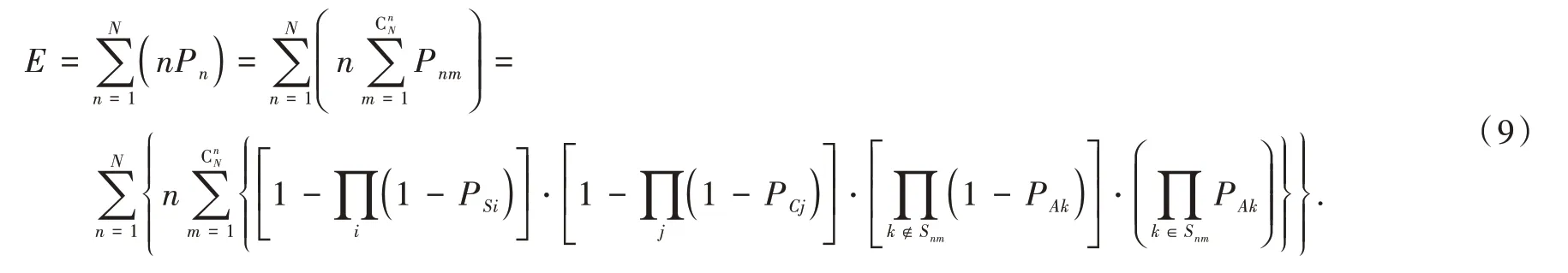
3 防御體系抗毀傷仿真計算
3.1 仿真場景設計
本文以典型防空作戰場景出發,敵方采用大規模空襲的方式對我國保衛要地開展攻擊,我方在要地附近部署3個偵察設備節點、3個控制設備節點以及10個打擊設備節點,通過組織防御作戰打擊鏈路,對敵方空襲目標進行打擊。依據實際攻防對抗場景,將我方各設備節點的生存概率進行設計,結果如表1所示。
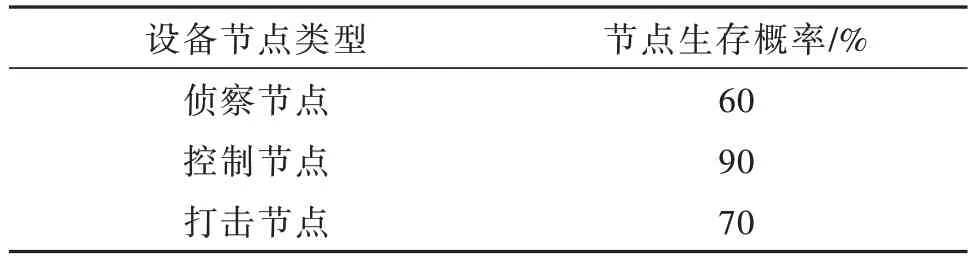
表1 設備節點生存概率表Table 1 Survival probability of equipment nodes
按照圖1中的結構,對傳統樹狀防御體系內資源要素間的關系進行建模。整個防御體系由3個獨立系統組成,每個獨立系統中包含1個偵察節點、1個控制節點和若干個打擊節點。
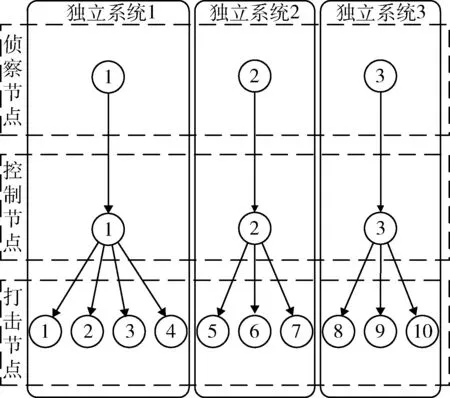
圖1 傳統防御體系結構圖Fig.1 Traditional defense architecture
按圖2中的結構,對分布式防御體系內資源要素間的關系進行建模。防御體系中的所有設備節點都存在于通信網絡之中,可以利用通信網絡實現任意2個設備間的信息交互。
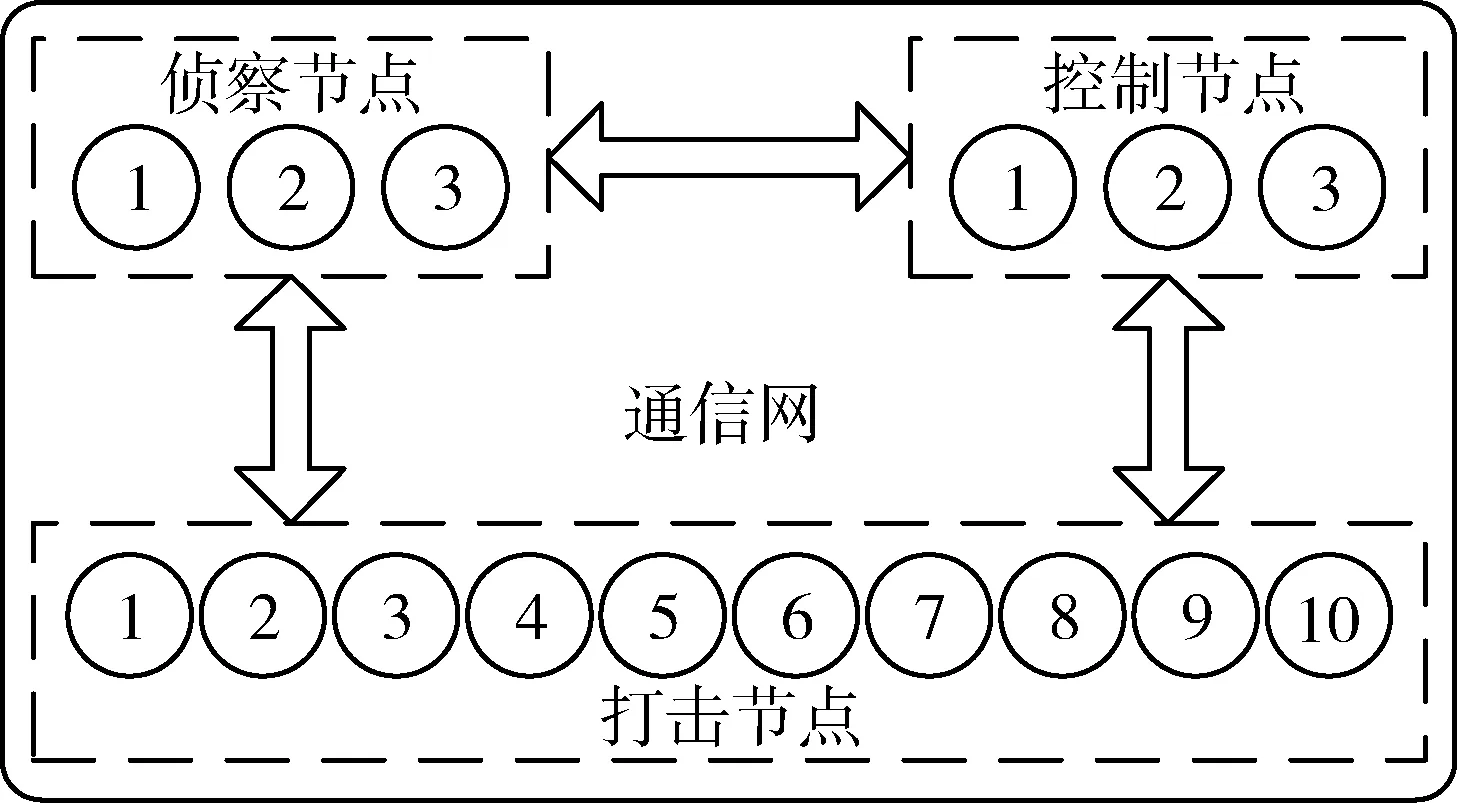
圖2 分布式防御體系結構圖Fig.2 Distributed defense ar chitectur e
3.2 仿真計算結果
根據上文所給的防御體系抗毀度量方法對防御體系的抗毀傷能力進行仿真計算,結果如表2所示。
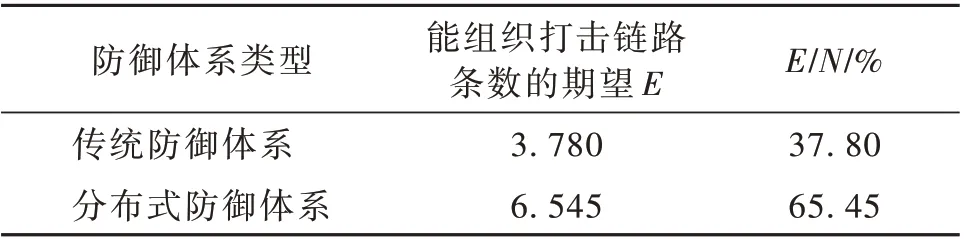
表2 防御體系抗毀性計算結果Table 2 Survivability calculation results of defense system
從表2中的計算結果可以看出,在相同的組成要素和相同的節點生存概率下,分布式防御體系能同時構建打擊鏈路條數的期望值要比傳統防御體系多2.765條。表格中的E/N反映了防御體系能保持體系防御作戰能力的程度。分布式防御體系在模型定義的節點生存概率下,能夠保持體系65.45%的防御作戰能力,而傳統防御體系只能達到37.80%。以上數據結果說明,分布式防御體系在體系抗毀能力層面具有明顯優勢。
3.3 節點數目增加對防御體系抗毀能力的影響
為研究節點數目增加對防御體系抗毀能力的影響,分別在2種防御體系中增加1個生存概率為60%的偵察節點、1個生存概率為90%的控制節點以及3個生存概率為70%的打擊節點。在對傳統防御體系進行計算時,這5個設備節點構成1個獨立的系統加入防御體系中;對分布式防御體系進行計算時,這5個設備節點直接接入分布式防御體系的網絡結構中。計算的結果如表3所示。

表3 防御體系抗毀能力與節點數目的關系Table 3 Relationship between survivability of defense system and the number of nodes
計算的結果表明,分布式防御體系能更好地發揮所增加設備節點的潛能,在增加相同設備節點的情況下,能更好地提高防御體系的抗毀能力。
3.4 節點生存概率對防御體系抗毀能力的影響
為研究不同環節的節點生存概率對防御體系抗毀能力的影響,本文通過變化其中一個環節的生存概率來進行計算與分析。計算結果如圖3所示。
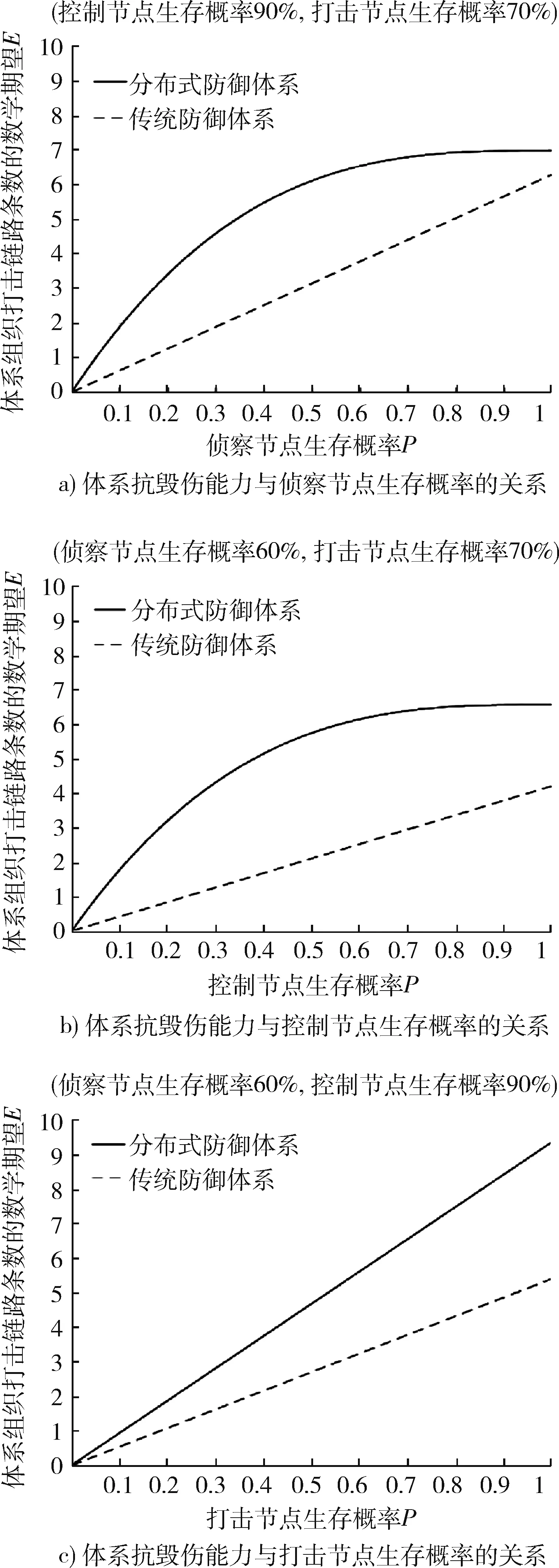
圖3 體系抗毀能力隨節點生存概率的變化曲線圖Fig.3 Variation curve of system survivability with node survival probability
從曲線圖可知,不管變化哪個環節的節點生存概率,分布式防御體系的抗毀能力都在傳統防御體系之上,這說明分布式防御體系的抗毀能力在不同節點生存概率下均具備一定的優越性。
4 結束語
本文先對不同防御體系的結構進行分析,分析了傳統防御體系與分布式防御體系在結構上的異同點。而后,結合概率計算的相關原理提出了一種傳統防御體系和分布式防御體系都適用的體系抗毀能力度量方法。最后,基于實際的作戰場景構建仿真模型,并利用體系抗毀能力度量方法對仿真模型進行計算與分析。整個過程解決了對分布式防御體系和傳統防御體系抗毀能力統一表征的難題,通過對2種防御體系的抗毀能力計算與分析,也驗證了分布式防御體系在體系抗毀能力層面的優越性。

