基于K-S檢驗的MIMO-STBC盲識別技術

金 堃，于柯遠，凌 青，閆文君

(1. 海軍航空大學航空基礎學院，山東 煙臺 264001；2. 海軍航空大學信息融合研究所，山東 煙臺 64001)

1 引言

通信信號盲識別技術是當今學術界和工程界研究的熱點[1]，無論是在軍事通信領域還是民用領域，通信信號盲識別技術都得到了廣泛應用[2-3]。空時分組碼(space-time block codes， STBC)的盲識別是指在接收端不知道信道狀態信息(channel state information，CSI)的情況下，只利用接收信號識別出發送端使用的空時編碼方式的技術[4]。它是通信偵察對抗領域迫切需要攻克的領域，具有重要的研究和軍事應用價值。

目前，有關STBC編碼類型盲識別算法主要分為基于最大似然算法和基于特征識別的算法，基于最大似然算法具有較好的識別性能，該方法需要預先估計信道，計算復雜度較高。基于特征識別的算法不需要對信道進行預估，但對時延和頻偏較為敏感且識別算法計算復雜度高，實時性較差，不利于工程化實現。文獻[5]提出了一種基于接收信號空時相關特性的STBC盲識別方法，通過構建一個線性空時編碼的分類器，利用接收信號統計量的Frobenius范數呈現非空值特性，判決STBC的編碼類型仿真結果表明，即使在較低的信噪比下，該方法也具有良好的性能。但該算法需要時間同步和預知信道信息，且計算量較大。

文獻[6]提出基于二階循環平穩的空時分組碼識別算法，和傳輸損耗條件下的STBC識別算法[7]。由于STBC碼矩陣內元素的相關性，不同STBC構成的接收信號具有不同的循環頻率，這可以作為識別的依據。兩篇文獻均采用特征檢測(Statistic Test)的方法對循環頻率進行檢測[8]。文獻[9]等人利用信號的空時冗余特征，提出了基于高階統計量的STBC信號盲識別算法，通過計算STBC信號的高階統計量矩陣，構造了信號的兩個特征參數，通過判別特征參數的值識別STBC信號類型，然而該算法容易受到信道衰落的影響。文獻[10]是首篇利用頻率選擇性衰落信道的衰落特性，提出了一種基于互相關函數的STBC分類算法。該算法通過構建AL-STBC的兩個不同接收信號的互相關函數在特定時延下存在峰值這這一特性，區分SM和AL-STBC，但該算法需要預知信道信息。文獻[11]提出了一種頻率選擇性衰落信道下的STBC盲識別算法，但算法數據利用率低，且只能識別兩種STBC編碼。

本文在單接收天線條件下提出了一種基于Kolmogorov-Smirnov檢驗的算法對頻率選擇性衰落信道下的單載波STBC盲識別。該算法首先對STBC信號和頻率選擇性衰落信道建模，以接收信號的經驗累積分布函數作為特征函數，通過K-S檢驗經驗累積分布函數之間的最大距離，將最大距離與不同時延下的門限值進行比較，從而判斷STBC的編碼方式。該算法具有以下優點：

1)適用于單接收天線系統，也可推廣到多接收天線系統；

2)將STBC識別推廣到四種STBC碼，且對信號的識別性能較為理想；

3)不需要預知STBC的調制方式以及信道信息，能夠實現信號盲識別。

2 信號模型

2.1 發射信號模型：

假設STBC系統具有Nt個發射天線，需要傳輸的信號序列為S=[s1，s2，…sn]，其中，每個序列中具有n個符號，且傳輸時隙為L，可表示為S=[Re(ST)，Im(ST)]T，發射端的信號矩陣矢量可表示為

C(S)=[A1S，…，ALS]

(1)

其中，Ai(0≤i≤L)表示發射端的STBC編碼矩陣。

2.2 STBC選取

STBC的正交設計方法較多，且大部分較復雜，本文選取空分復用(SM)、Alamouti碼、STBC3和STBC4四種空時分組碼作為研究對象，其編碼方式如下。

SM是一組nt個符號通過nt個天線發射的STBC，碼矩陣長度L=1

C(S)=sj，j=1，…，NTx

(2)

AL碼是一組2個符號通過兩根傳輸天線發射的STBC，碼矩陣長度L=2

(3)

STBC3碼是一組三個符號通過三根傳輸天線發射的STBC，碼矩陣長度L=4：

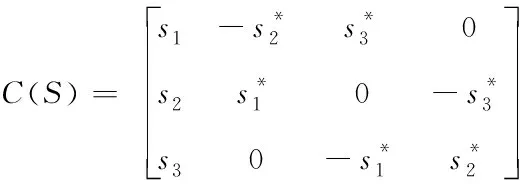
(4)

STBC碼是一組四個符號通過四根傳輸天線發射的STBC，碼矩陣長度L=8：

(5)

復正交設計的最大碼率可表示為R=N/T，如STBC3在T=4的符號周期內發送N=3個符號(x1，x2，x3)，因此STBC3的碼率是r=3/4，同理STBC4的碼率r=1/2。

2.3 接收信號模型：

假定STBC系統具有Nr個接收天線，假設r(0)為第一個接收符號。在頻率選擇性信道中，接收符號可以表示為多個發射符號加權求和的形式，STBC信號在經歷頻率選擇性衰落信道后，第k時刻接收到的符號可表示為

(6)

其中，path代表頻率選擇性衰落信道中存在的路徑條數，hi(p)代表第p個路徑的信道系數，w(k)代表信道中存在的高斯白噪聲。

3 算法分析

3.1 基于K-S檢驗的盲識別算法

K-S檢驗是對于信號樣本的經驗累積分布函數的一種非參數最佳擬合檢驗。通過K-S檢驗可以識別假設中的兩個信號樣本是否屬于同一分布，以此作為特征參數，對STBC信號的類型進行識別。

假設接收端接收信號序列為

y=[r(0)，r(1)，…r(K-1)]

(7)

其中，r(k)為接收天線接收到的k時刻符號，K為接收符號數量。

將接收到的信號序列分成獨立的兩部分，其相關函數向量如下所示

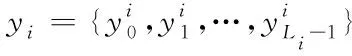
(8)

(9)

其中，Li為序列yi的長度，Ni為序列zi的長度。

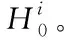
其中card(.)為指示函數，若輸入為真，則函數值為1，否則函數值為0。

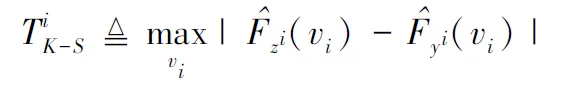
(12)

P(=Hi0|Hi0)=P(TiK-S<λi|Hi0)=βi

(13)

(14)

其中

(15)

根據四種STBC的編碼方式，分別在時延τ=1， 2， 4時，對接收到的信號序列進行分段處理。

當時延參數τ=1時，可從信號中識別出SM編碼，按如圖1所示的分段方法將接收信號序列分成獨立的兩部分

(16)

(17)

其中，K為接收信號的長度，?.」為向下取整函數，2個信號序列的長度分別為2?K/4」和K-2(?K/4」+1)。

圖1 τ=1時信號序列劃分方法

在圖中，L1=2?K/4」，N1=K/2-?K/4」-1，當時延參數τ=1時，如圖1所示構造的相關函數可表示為

(18)

(19)

根據式(9)(10)可得，相關函數向量可表示為

(20)

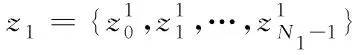
(21)

當SM傳輸的時候，其中y1跟z1是獨立同分布的；當AL、STBC3、STBC4傳輸的時候，y1跟z1不一定是獨立同分布。

采用K-S檢驗來估計y1跟z1的兩個向量的經驗累積分布函數最大的分布

(22)

當τ=2時，可從信號中識別出AL編碼，按如圖2所示的分段方法將接收信號序列分成獨立的兩部分

(23)

(24)

其中，兩個向量的長度L2=2?K/4」，N2=K/2-?K/4」-1。

圖2 τ=2時信號序列劃分方法

當時延參數τ=2時，如圖2所示構造的相關函數可表示為

(25)

(26)

兩個相關函數向量可表示為：

(27)

(28)

同理可得，當AL信號傳輸時，y2跟z2是獨立同分布的，而對于STBC3，STBC4，y2跟z2兩個不同時是獨立同分布。

采用K-S檢驗來估計y2跟z2的兩個向量的經驗累積分布函數最大的分布

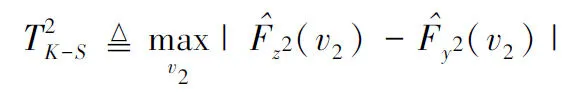
(29)

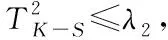
同理，當時延參數τ=4時，可從信號中區分出STBC3、STBC4兩種編碼。按如圖3所示的分段方法將接收信號序列分成獨立的兩部分

(30)

(31)

圖3 τ=4時信號序列劃分方法

其中，兩個向量的長度L3=2?K/4」，N3=K/2-?K/4」-1。當時延參數τ=4時，如圖3所示構造的相關函數可表示為

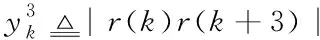
(32)

(33)

兩個相關函數的向量可表示為

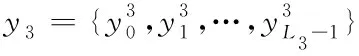
(34)

(35)

同理可得，當STBC3信號傳輸時，y3跟z3是獨立同分布的，而對于STBC4，y3跟z3兩個不同時是獨立同分布。

采用K-S檢驗來估計y3跟z3的兩個向量的經驗累積分布函數最大的分布

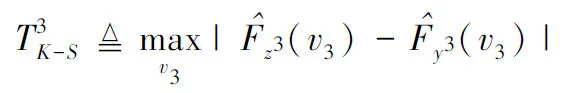
(36)

上述對STBC信號的識別過程利用了假設檢驗以及決策樹理論，其流程如圖4所示。

圖4 STBC信號決策樹識別流程

4 性能分析

4.1 仿真條件設定

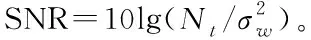
其中，θ∈{SM，AL，STBC3，STBC4}。

4.2 算法性能分析

仿真1：識別STBC的性能

仿真1討論算法對四種STBC信號的識別概率，采用正確識別概率衡量算法性能，如5圖所示。SM的識別概率與信噪比無關，其識別概率為N∈{8， 10， 12}，保持在99%。隨著信噪比的增大，AL、STBC3、STBC4的識別性能逐漸提高，AL、STBC4信號在0dB時基本達到95%以上，而STBC3信號識別性能不理想，在14dB時才達到95%左右。這是由于在STBC3的編碼矩陣中有0項，使得經驗累積分布函數的距離變小，不容易被識別。而隨著信噪比的增大，抑制了噪聲對經驗累積分布函數的影響，從而提升了算法對STBC信號的識別性能。

圖5 不同STBC正確識別概率

仿真2 調制方式對算法識別性能的影響

仿真2討論K-S識別算法在QPSK、BPSK、8PSK三種不同調制方式下的識別性能，采用四種STBC碼的平均識別概率來衡量，如圖6所示。其中BPSK調制方式下的算法識別性能最好，在信噪比為-2dB時識別概率基本達到95%以上，因為BPSK調制的是實數信號，信號傳輸性能更好；QPSK調制方式下的識別性能比8PSK要稍好一些，但相差不大。

圖6 調制方式對算法識別性能的影響

仿真3：置信區間對算法識別性能的影響

仿真3討論置信區間對算法識別性能的影響，算法分別在三種置信區間下進行仿真，如圖7所示。本節仿真采用兩種識別概率衡量算法性能，一種是SM算法的正確識別概率，另一種是AL、STBC3、STBC4三種碼正確識別的平均值。隨著置信區間N∈{8， 10， 12}增大，SM的正確識別概率隨之減少(識別概率為N∈{8， 10， 12})，而三種STBC的平均識別概率在N∈{8， 10， 12}值時識別效果更理想。根據式(16)可知，置信區間N∈{8， 10， 12}增大，門限值λ也隨之增大，因此識別概率也隨之增大。

圖7 不同置信區間下的正確識別概率

仿真4：采樣因子對算法識別性能的影響

仿真4討論采樣因子對算法性能的影響，分別在N∈{8， 10， 12}時進行仿真，采用平均識別概率衡量算法性能，如圖8所示。采樣因子為12時，算法在2dB的識別概率就能達到95%以上，而采樣因子取10和8時，要達到這一效果分別在6dB和12dB。采樣因子的增大，使得對接收信號的采樣數增加，即y(x)，z(x)的元素增多，減少了噪聲和信道對經驗分布函數的干擾，使得識別效果更理想。

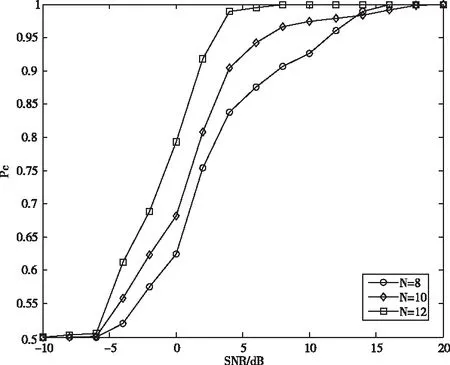
圖8 采樣因子對算法性能的影響

仿真5：與其它算法識別性能的比較

目前，頻率選擇性衰落信道下單載波傳輸的STBC識別算法僅有一篇文獻，將本文中的算法與文獻中最大似然算法和虛警率識別算法分別進行比較。因文獻中只采用了SM和AL兩種空時分組碼，本文算法也只選取了SM和AL兩種碼的正確識別概率進行對比。同FAR算法相比，本文算法的識別性能有顯著提高，尤其在低信噪比情況下，算法識別性能提升了約20%。

圖9 本文算法與FAR算法性能比較

5 結論

本文在單接收天線條件下，提出了一種在頻率選擇性衰落信道下的STBC盲識別算法，主要工作和結論如下：

1)該算法通過K-S檢驗接收信號在不同時延下的經驗累積分布函數之間的距離，與門限值對比，采用決策樹分類以達到識別STBC的目的。

2)本文中提出的K-S檢驗算法提高了樣本的利用率，且算法將接收天線的數量延伸到單天線條件下，適用于四種STBC信號的盲識別，算法更具普遍適用性。

3)仿真結果表明，本文算法對調制方式不敏感，但其識別性能隨著采樣因子和置信區間的增大而增大，且該算法不需要預知信道、噪聲等信息，適合于非合作通信場合。

4)將本文算法與僅有的一篇在頻率選擇性衰落信道下識別單載波傳輸STBC文章中的算法進行了比較，在高信噪比時本文算法的識別概率趨近于1，但在低信噪比條件下的算法識別概率并不是十分理想，識別概率仍有待提高。本文所提出的算法在信噪比具有95%以上的正確識別概率，且算法適用于單接收天線等極端情況，適用范圍廣，適合進一步工程應用。