機床用基于加性分解PMSM的滑模控制＊

劉慧博 陳豪鑫

（內蒙古科技大學信息工程學院，內蒙古 包頭 014010）

永磁同步電機（PMSM）因為其高可靠性，高效率和高性能而常被用于各業中，像在陸地交通（如機床）、航海交通（如船舶推進）和軍事（如自行火炮）等領域已司空見慣。然而，PMSM是一個變量多、非線性、強耦合的系統[1]，并且機床運行中會受到許多外部干擾，負載轉矩會不斷改變，讓PMSM控制變得尤為復雜。傳統V/F控制技術已沒法適應現代機床對轉速、轉矩持續穩定調控和抗干擾能力要求。隨后，出現了一種可以把交流電機類似簡化成直流電機的控制-磁場定向控制（field oriented control，FOC），因其擁有動態的高速響應、全速波動小及靈便控制等優點，現被廣泛應用于PMSM控制上。其控制調節通常包括轉速環和電流環，且都能根據相應指令實時跟蹤，對外部干擾具備較強的魯棒性。電流環內部電流控制回路直接影響驅動系統的性能，需要精確的跟蹤性能[2]。對此采用電流雙閉環進行跟蹤控制，該結果能很好地控制機床的運行狀態。對于轉速外環系統，會受到動態的變速和變載等不確定性外部干涉，要達到轉速持續調穩目的較為困難。為此，文獻[3]采用滑模轉速控制器替代傳統型的PI速度調節器，增強了系統的魯棒性，拓寬了系統的調速范圍，但抖振較大。文獻[4]設計了基于新型指數趨近律的滑模變結構速度控制器，仿真和實驗結果表明,該速度控制器的高頻抖振略微減弱，也有效地提高系統的靜態、動態特性與魯棒性。

加性分解（additive decomposition，AD）理論，是一種可以使復雜大系統分解為兩個簡易小系統的疊加，這樣就能很好地在簡易小系統內完成各自問題，進而實現復雜的原始系統控制。文獻[5]將該理論實現在風力機變槳控制器設計中，使原復雜的非線性系統，分解為2個簡單的控制問題。文獻[6]策略是將跟蹤子任務分配給主系統，將穩定子任務分配給輔助系統，因此主系統可以使用頻域或時域中的標準設計方法，而輔助系統就可以采用許多非線性穩定控制方法。光電跟蹤系統作為典型的伺服系統，已被證明可運用加性分解理論對其進行主、輔系統控制，進而完成對目標的高精度追蹤。而永磁同步電機控制系統也是一個典型的伺服系統，因此對其控制任務可分為：轉速環的穩定控制和電流環的跟蹤控制。

綜上所述，本文將基于加性分解理論對PMSM控制系統進行分解成主系統和輔系統，將電流矢量位置跟蹤控制和轉速環穩定控制對應在主、輔系統內完成。因為機床運行狀況一般是低速行駛和受負載擾動，經以往實驗經驗知道滑模控制抗干擾力優于PI控制（如文獻[3]），所以將采用速度滑模調節器。再對比傳統速度滑模控制方法，驗證了所設計的改進滑模控制方法能夠對PMSM進行更高效穩定控制。

1 基于加性分解的數學模型

機床伺服控制系統主要由PMSM、驅動電路、編碼器、平臺框架系統及電源組成。其機電系統動態模型可以表示為:

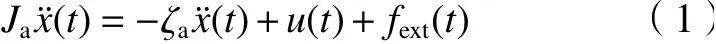
式中：Ja為 系統的轉動慣量；ζa為系統的阻尼系數；u(t)為 系統的控制輸出；fext表示外部干擾。因此，PMSM驅動控制系統的狀態方程可表示為

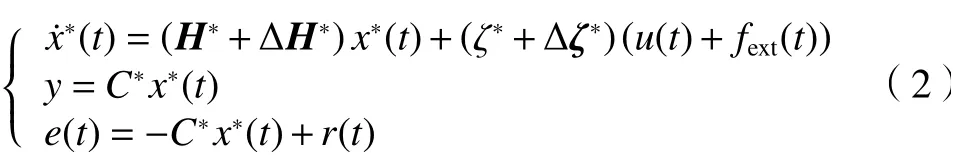
其中的 ζfext(t)可完全展開為：

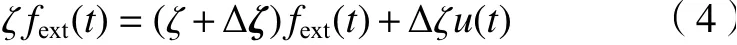
將原系統與主系統相減得輔系統，即

最后，可看出用加性分解理論對系統進行分離后，可以將外部干擾穩速問題和跟蹤問題分開處理，進而實現高效控制。基于加性分解PMSM控制系統框圖如圖1所示。

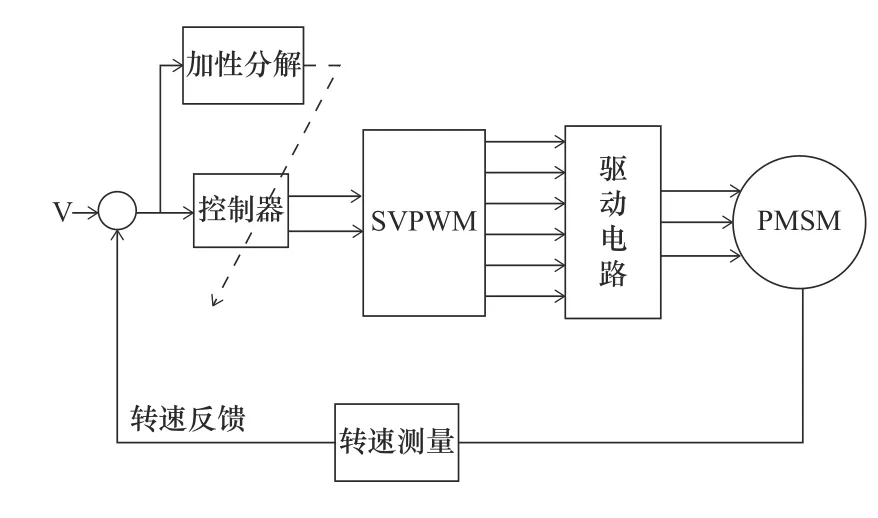
圖1 基于加性分解PMSM控制系統框圖

2 基于加性分解的控制策略

為了實現PMSM的穩速控制（steady speed control，SSC），從系統給定轉速出發，針對輔系統模型首先設計基于滑模的轉速調節器。主系統為了完成電流矢量精確控制，也就是電流跟蹤控制（current tracking control，CTC），設計采用雙閉環電流跟蹤控制器。經加性分解后的控制器框圖如圖2所示，其中r(t)是給定轉速信號，通過與轉速反饋閉環比較后，經過SSC后實現對系統轉速上的穩定調節。后由輔系統調節產生的電信號流經CTC，主系統對其交直軸電流進行有效分配，實現對電流矢量的精確控制，從而完成控制器的有效輸出y(t)，最后實現對PMSM的高性能控制。

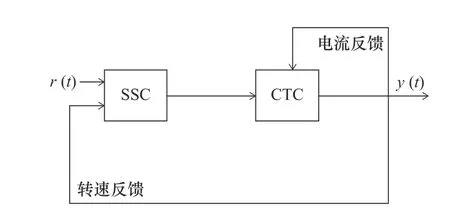
圖2 加性分解后的控制器框圖

3 輔系統控制器設計

3.1 傳統速度滑模控制器的設計

滑模控制(SMC)可以使系統在一定條件下沿規定的狀態軌跡作小幅、高頻率的上下運動，這就是所謂的“滑動模態”[7]。這種滑動模態是可以設計的，并且與系統的參數和擾動無關[1]。所以，滑模控制的強魯棒性就是這么而來。

為了設計滑模速度調節器，由圖2知，令輸入為 Δw， 輸出為iq。 首先定義調節器的狀態變量為x1=wr-w,x2=x˙1， 其中wr為 參考輸入，w為真實轉速。于是可得到：

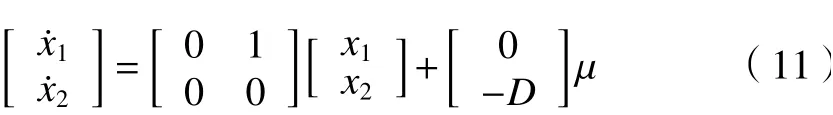
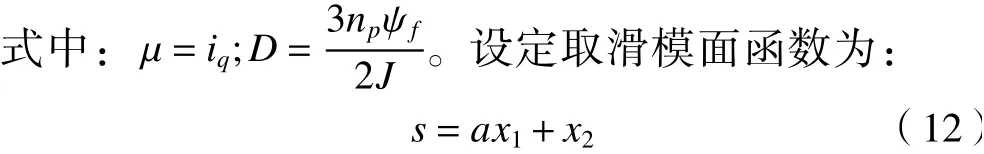
式中：a為設計參數，a＞ 0。對式（12）兩邊求導，則有：

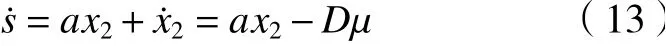
為了實現控制調節器優良的動態響應，摒棄一般趨近率而采用指數型的（ ε＞0），所以得滑模控制器的表達式為：

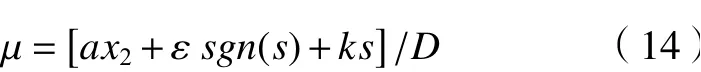
于是通過積分計算可得到iq的參考值為 ：

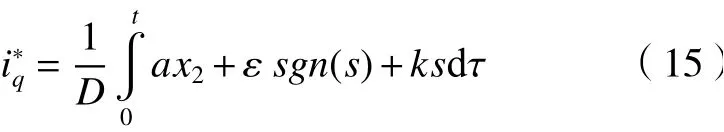
由李雅普諾夫（Lyapunov）定理和滑模到達條件s˙s＜0，證明系統是漸進穩定的。根據PID理論知，控制器中含有積分，可使抖振削弱些，也就可減小穩態誤差；但抖振依然明顯，所以下節將進行改進滑模的設計。

3.2 改進速度滑模控制器的設計

滑模的抖振是肯定會存在的，若是完全消除那也就會消除SMC的強魯棒性，因此只能盡可能削減。其產生抖振現象的主要緣由是非理想的切換、慣性影響和測量誤差，而 ε還決定動態滑模的運動品質。

所以本文改進速度滑模控制器主要是針對ε進行優化，將傳統控制器中切換項系數改進為其中 λ為待調節參數，這里將切換項引入誤差絕對值項 |e|，在系統逐漸趨于滑模面時,誤差絕對值逐漸到0，將切換項占比拉低，繼而削弱系統產生的抖振程度。又因系統運行時是不斷地變化、權重更新，所以也提高系統的自適應能力。依據上述推論，基于改進滑模控制時的控制量最終表達式如式(16)所示。

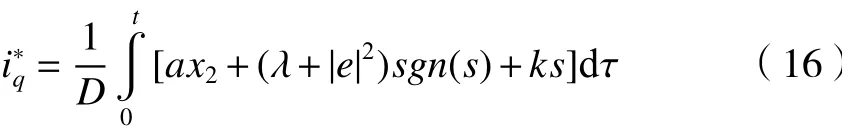
4 主系統控制器設計

機床伺服驅動控制系統既要考慮轉速還要考慮電流的轉矩輸出能力，而且對電流環的跟蹤作用也能使系統具有良好的動態響應效果。所以對交直軸電流進行跟蹤分配，這樣做能夠提升系統的動態響應，又可以增加單位電流輸出轉矩的能力。

設定子電流is與d軸的夾角為β，則d、q軸電流可以表示為

再結合式（18）的電磁轉矩公式

得到電磁轉矩電流比，即

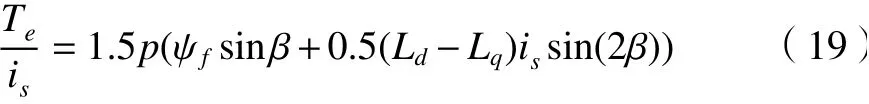
此時對控制轉矩角的條件求解可轉換為數學問題，即根據式（19）對β求偏導，可得

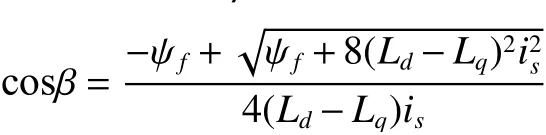
5 仿真結果和分析

為驗證用加性分解PMSM的改進滑模控制方法的有效性，構建了如圖3所示的控制系統結構框圖。

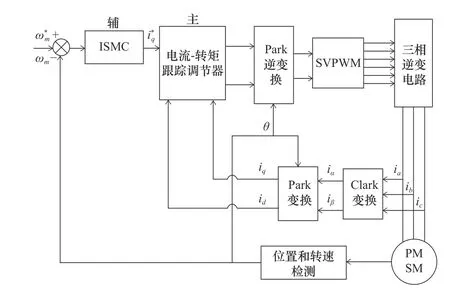
圖3 基于加性分解PMSM的控制系統結構框圖

在Matlab環境下建立了系統仿真模型仿真，仿真中所用電機的參數設置為：極對數4，Ld=5.25mH,Lq=12mH，定子電阻R=2.87 Ω，磁鏈是0.175 Wb，轉動慣量J=0.003 k g·m2， 阻尼系數為0.008 N·m·s。

輸入低轉速100 r/min，初始時刻空載運行，在時間0.2 s時突施10 N·m的轉矩TL，仿真如圖4所示。由圖4可知（右邊是經過加性分解結構的，左邊是未經加性分解的），明顯對比出傳統SMC控制經加性分解后具有更好的動態響應和穩態性能；尤其是在突施負載時，后者掉速明顯比較小且恢復時間較短，因此效率更快。由圖5也看出，經加性分解控制后的轉矩波動更小，抗干擾能力強。

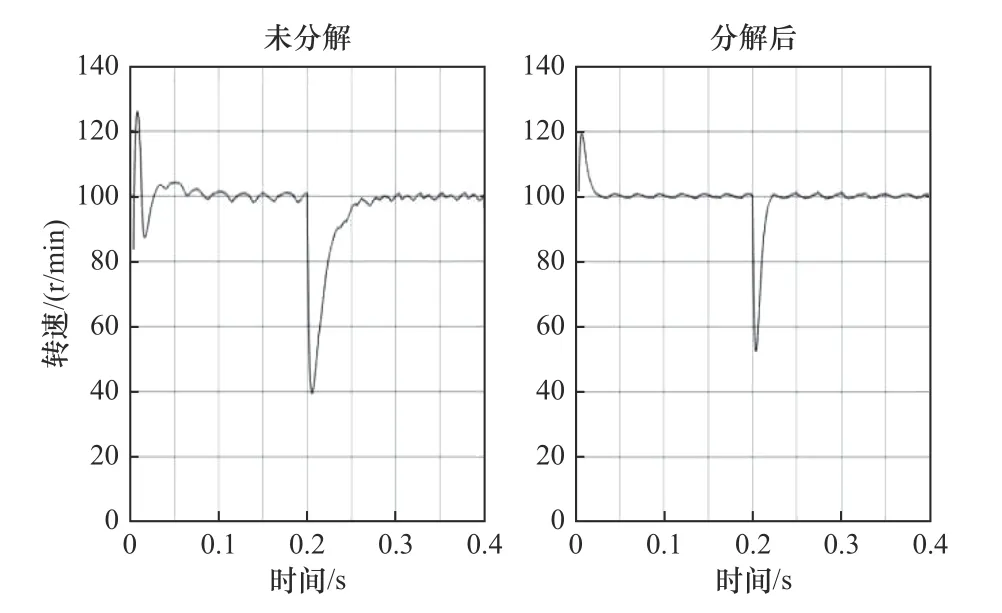
圖4 轉速響應曲線

圖5 電磁轉矩響應曲線

盡管如此，還是解決不了傳統SMC固有的抖振問題，因此進一步分析了改進滑模控制。如圖6所示為改進SMC后的轉速響應曲線，再由其圖7的改進前后對比分析知，在結合加入誤差絕對值反饋后，改進滑模控制器在系統運行時持續調整，提高系統的自適應能力，削弱了傳統SMC的抖振問題，平滑運行，印證了所提方法的有效性。

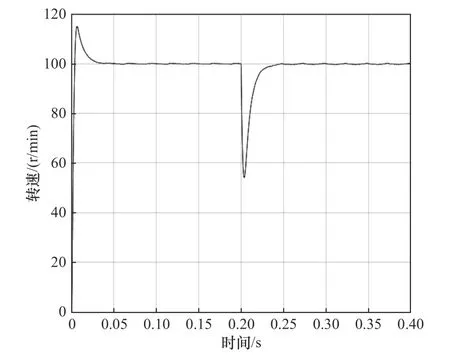
圖6 改進SMC轉速響應曲線

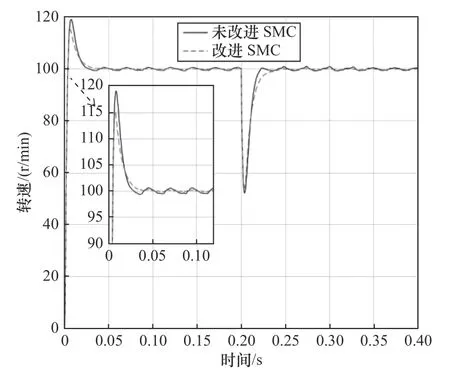
圖7 改進SMC前后對比

6 結語

本文設計了一種基于加性分解原理的PMSM控制方法，將系統的控制任務分別在主系統和輔系統內完成。該方法在保證系統穩定的基礎上，不僅簡化了控制過程，而且可以提高對PMSM控制精度以及系統的動態品質。仿真試驗證明，本文所提的結構復合控制方法，拓寬了調速范圍，增強了帶載能力和抗干擾能力，削弱了傳統滑模所固有的抖振，符合機床電機運行要求。該方法簡單實用，易于實現，對工程應用具有一定參考價值。