基于Kriging-MIGA算法的薄壁件銑削參數優化＊

韓 軍 曹龍凱 徐 睿 姚 晟 熊鳳生

（①內蒙古科技大學機械工程學院，內蒙古 包頭 014010；②山東港口集團青島港國際股份有限公司前港分公司，山東 青島 266000）

隨著航天科工領域的快速發展，薄壁零件由于質量輕和比強度高等優點被頻繁地使用[1]，薄壁件在生產中的銑削參數選擇常常對銑削力和工件變形等有著重要影響，而實際銑削參數常常是技術人員根據經驗選擇的，所用參數不是最優銑削組合，導致加工過程中因銑削力過大等原因造成工件變形，不易保證被加工零件的公差尺寸，生產效率也不高[2]。因而研究薄壁件銑削參數優化具有重要意義。

隨著智能優化算法不斷的發展與完善，越來越多的學者將其用于銑削參數的優化中。曾莎莎[3]等采用了倒傳神經網絡的方法，優化工藝參數組合。Liang M等[4]采用模糊控制方法，對銑削時的參數進行了優化。鄧偉[5]以最小能耗為目標，基于粒子群算法開展銑削參數的優化。雖然上述研究取得了預期效果，但所用算法較復雜，優化過程較長，而MIGA算法不僅優化速度快，且全局收斂快，計算效率高。姜佳明[6]采用了響應曲面法對蜂窩薄壁件開展高速切削參數優化，提高了切削加工效率，但響應面模型的建立需要大量的樣本點，較為繁瑣，而Kriging模型在搭建過程時，所需樣本點數較少，且全局精度高。

針對上述問題，本文以某薄壁殼零件為研究對象，通過Isight平臺，采用了最優拉丁超立方試驗方法建立樣本點，研究主軸轉速、徑向切深和軸向切深對銑削力的影響規律，擬合銑削參數與銑削力間的Kriging近似模型，以銑削力最小為目標，采用MIGA算法優化得出最合適的銑削參數組合。

1 試驗方案

零件的尺寸要求如圖1所示。

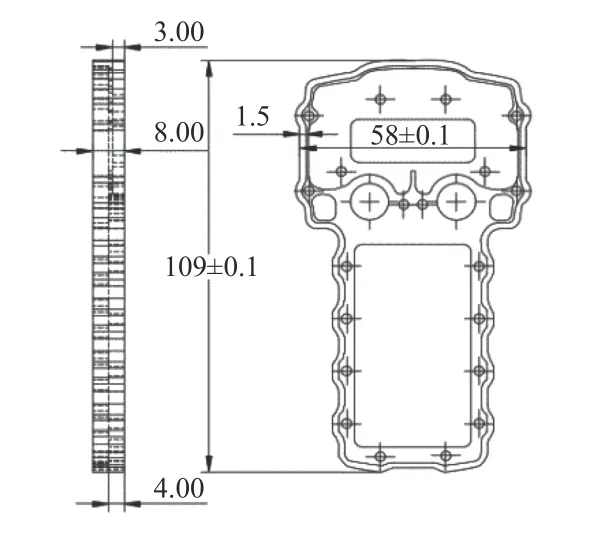
圖1 薄壁框二維圖

該薄壁零件毛胚材料為6061鋁合金，材料剛性較差。同時，因為毛坯自身殘余應力的影響，加工后，殘余應力得到了相應的釋放，會引起零件特別是薄壁件的變形，故為了避免有過多的外力因素作用，更好的研究銑削力與銑削參數對薄壁件變形的影響，需要先對裝夾方式進行確定。由于零件較薄，壁厚僅為1.5 mm，故不能采用虎鉗、真空吸盤等傳統裝夾方式。結合6061鋁合金的材料特點和薄壁零件的結構特征，提出了采用在毛坯背面覆膠的裝夾方式，使其固定在工作臺上，這種方式避免了夾具與零件的直接接觸，只需要在加工中預留0.1 mm的余量，也就是總厚度為8 mm的薄壁零件，在外輪廓加工時，下切深度到7.9 mm，待加工完畢后，將整個毛胚取下，剩余的0.1 mm余量做去毛刺處理，裝夾如圖2所示。

圖2 薄壁件裝夾圖

確定裝夾方案后，對薄壁零件進行銑削，加工完成后，使用惟德Tomoscope S型復合式坐標測量儀進行測量，發現其輪廓尺寸分別為109.13 mm和58.16 mm，不符合圖紙公差要求，通過多次銑削實驗，發現在半精加工階段時（主軸轉速3 000 r/min，徑向切深1 mm，軸向切深1 mm，銑刀直徑為10 mm、齒數為 4、前角 5°及后角 15°）因銑削參數選擇不合理造成銑削力過大，是導致薄壁零件變形量過大的主要原因之一。

2 試驗設計與結果

為獲取銑削參數與銑削力之間的近似模型，采用Isight試驗設計算法庫中的最優拉丁超立方設計方法先行設計樣本點，該方法設計的樣本點具有均勻性好、可靠性高等優點。根據現場加工經驗選取銑削參數范圍：主軸轉速2 500～6 000 r/min，徑向切深0.5～2 mm，軸向切深0.5～3 mm，設計的30組樣本點和對應的銑削力，如表1所示。

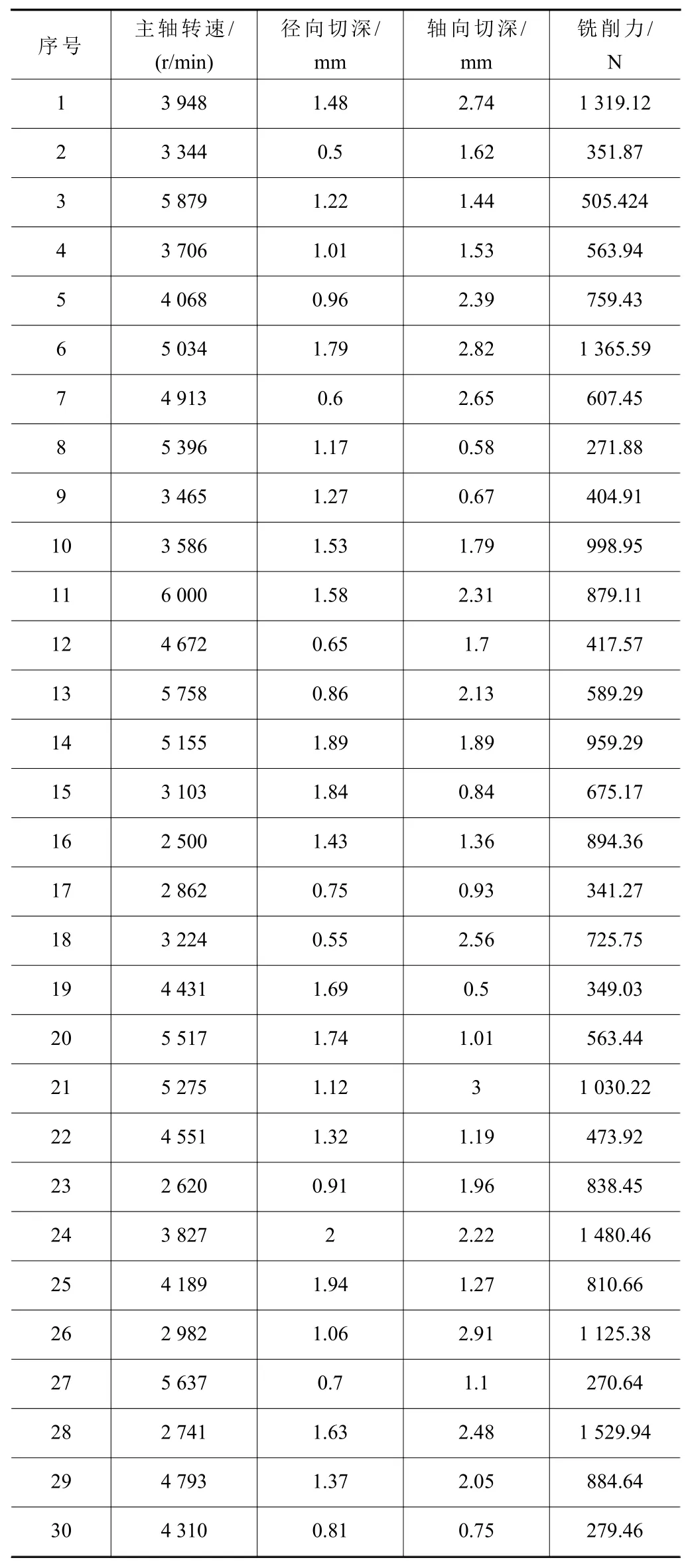
表1 試驗設計樣本點

3 基于Kriging-MIGA算法的優化方案

基于Kriging-MIGA算法的優化步驟如下：

（1）采用最優拉丁超立方試驗設計方法設計主軸轉速、徑向切深和軸向切深3個銑削參數的樣本點，通過實驗得出樣本點對應的銑削力。

（2）根據樣本點，搭建銑削參數與銑削力之間的Kriging近似模型。

（3）以銑削力最小為優化目標，采用MIGA算法對銑削參數進行優化。

（4）獲得銑削力的最小值，輸出對應最優銑削參數組合。

Kriging-MIGA算法流程如圖3所示：

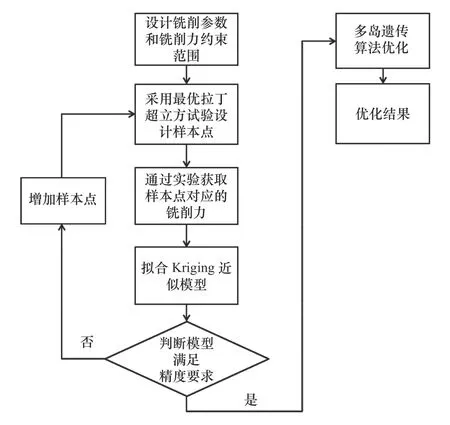
圖3 Kriging-MIGA算法流程圖

4 銑削參數的優化

4.1 近似模型的建立

Isight平臺中的Kriging近似模型屬于半參數化插值技術，在樣本點中對未知點插值具有很高的精度，對非線性關系擬合效果較好，常由回歸部分與隨機函數組合而成[7]。同時，由于Kriging的半參數化性,因而不需要搭建特定的函數模型[8]，相比其他近似模型技術，會更加方便與靈活。

給出樣本點x集合，對應的響應為y，樣本與響應間的Kriging近似模型數學表達式如式（1）所示。

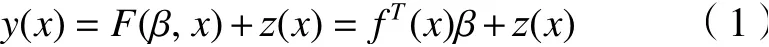
式中：β為回歸系數；fT(x)為默認為高斯函數；z(x)為 隨機誤差；z(x)的統計特性[9]如式（2）所示。

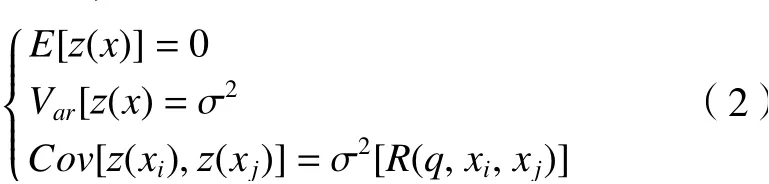
式中：xi、xj為 樣本中任意兩點；R(θ，xi，xj)為表示樣本的空間相關性。

根據最優拉丁超立方試驗設計的樣本點，通過Kriging近似模型方法，構建銑削參數與銑削力之間的近似模型。

構建Kriging近似模型時，銑削參數與銑削力之間至少需要2n+1個設計樣本點[10]，其中變量n為銑削參數的個數，由表1可知n=3，而本文設計了30個樣本點，故滿足分析要求，近似模型如圖4所示。

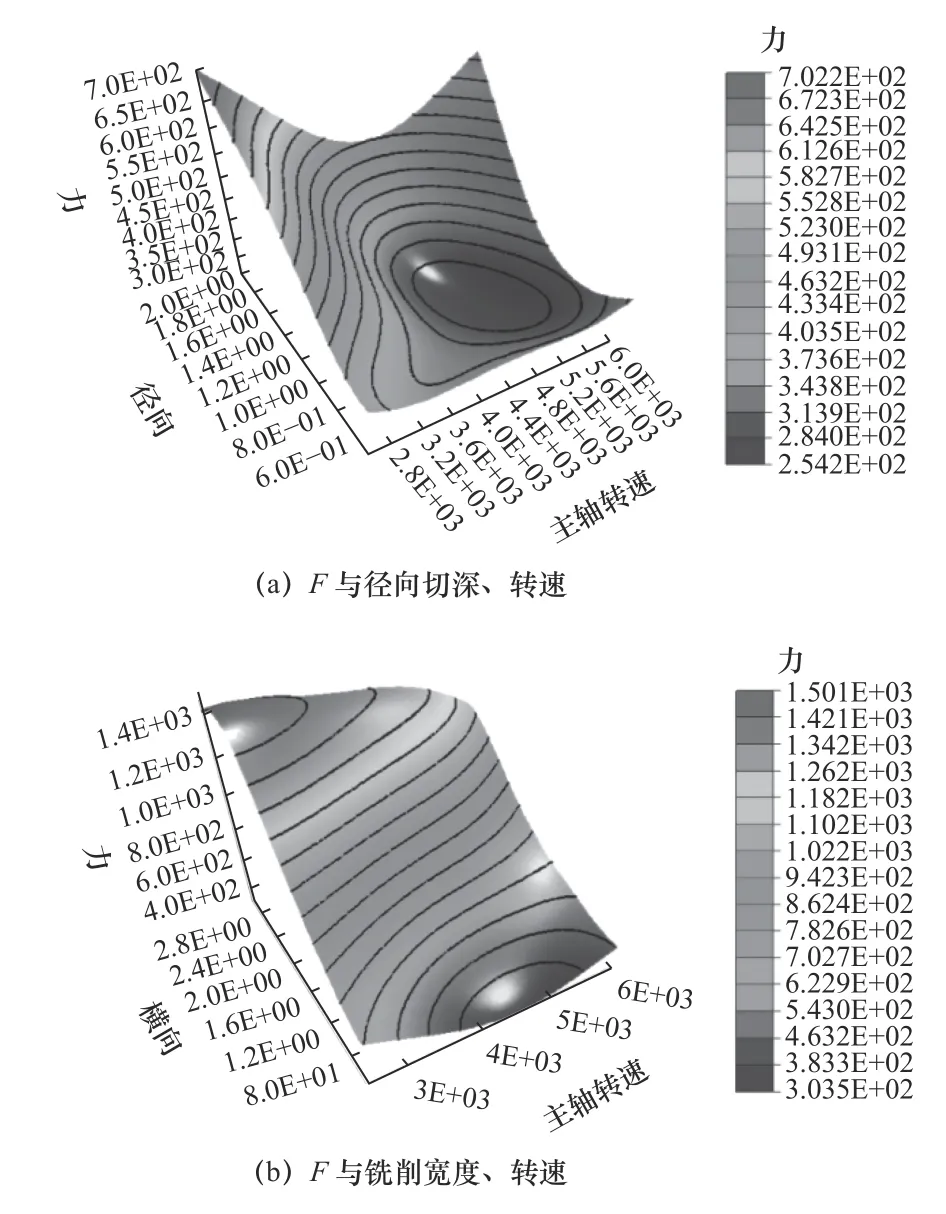
圖4 近似模型圖

為保證近似模型的精度，根據試驗方法選取樣本點開展誤差分析，采用可決系數評估擬合精度[11]，其表達式為

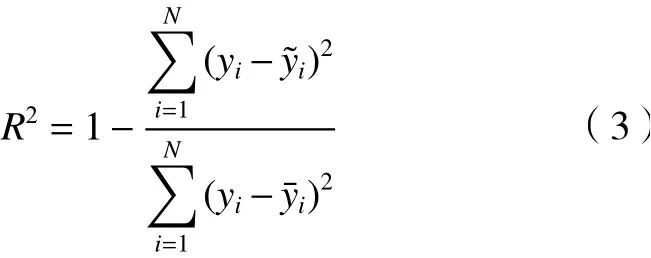
式中：N為試驗次數；為 預測值，yi為模擬值。

根據計算可知R2=0.935，當可決系數大于0.9的時候[12]，Kriging近似模型達到精度要求，即模型是可靠的。

4.2 MIGA算法的優化

MIGA算法屬于改進后的并行遺傳算法，相比傳統的遺傳算法，不同之處在于MIGA算法把種群比作“島”，多個種群便有多個島，每個島上獨立地進行遺傳算法尋優，大大提升了全局優化能力，其特點有：

（1）在使用MIGA算法時，需要將優化問題的解進行編碼，目的是為了形成類似染色體的鏈碼，每一個鏈碼即為1個個體，多個個體便組成種群。MIGA算法的編碼為格雷碼編碼[13]，如式（4）所示。

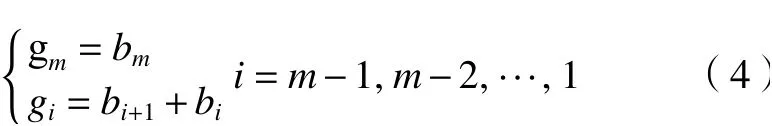
（2）MIGA算法將種群分成多個島，為了能選出島中最優的個體，增加島內個體的多樣性，島與島之間常會產生遷移、選擇等行為。

基于銑削參數與銑削力之間的近似模型，在Isight 平臺的Optimization模塊里采用MIGA算法對模型進行尋優。同時，算法優化之前，以銑削力最小為優化目標，對相關銑削參數進行約束，約束條件如式（5）所示。

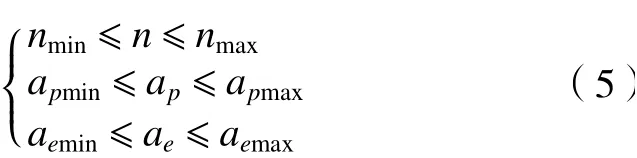
式中：n為主軸轉速；ap為軸向切深；ae為徑向切深。

MIGA算法參數設置如表2所示。

表2 多島遺傳（MIGA）算法參數配置

相關參數與約束設置成功后，進行優化，迭代過程如圖5所示。

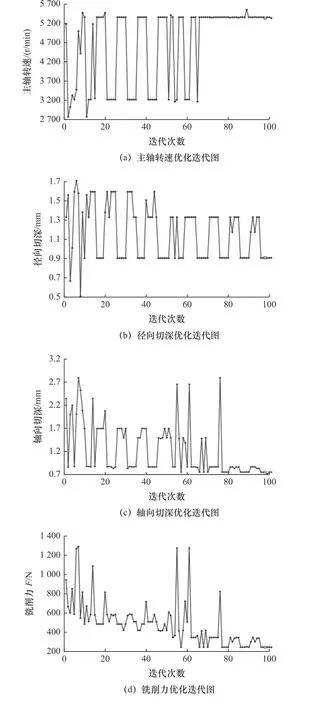
圖5 MIGA優化迭代圖

MIGA算法在全局尋優的過程中，相應的目標變量在不斷地收斂，雖然初始跳動較大，但達到80代后，目標變量逐漸平穩，偶爾因交叉變異出現較小的波動[14]，90代后多島遺傳算法出現最優解。

5 優化結果分析

銑削參數與銑削力在優化前后的結果對比如表3所示。

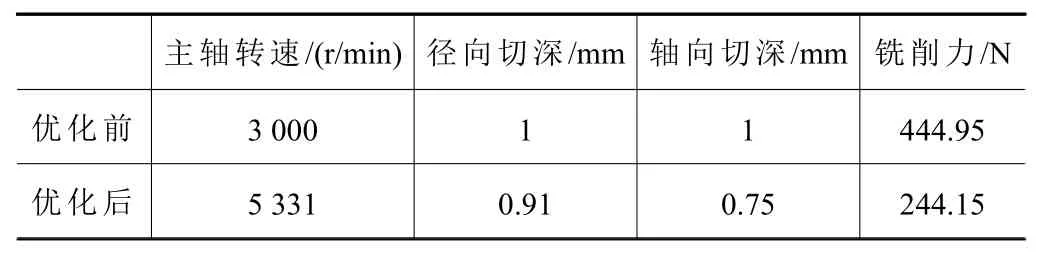
表3 優化結果對比

將優化后的銑削參數組合（主軸轉速5 331 r/min，徑向切深0.91 mm，軸向切深0.75 mm）應用到現場實驗加工中，銑刀與工件材料的選擇與優化前一致，所得結果為269.79 N，而通過MIGA算法優化所得的銑削力為244.15 N，兩者誤差為9.5%，誤差產生的原因是因為薄壁件實際銑削中會有熱變形以及機床振動等影響因素的存在，只要誤差在合理范圍內，就可以認為Kriging近似模型準確擬合出了銑削參數與銑削力之間的關系。此時，銑削力從原先的444.95 N減小到269.79 N，減小了39.37%。

6 實驗及結果分析

將毛坯裝夾于德瑪吉DMU50數控加工中心，在半精加工階段采用優化后的銑削參數組合進行銑削，加工后工件如圖6所示。

圖6 加工工件

使用惟德Tomoscope S型復合式坐標測量儀對工件進行驗證，結果如表4所示。

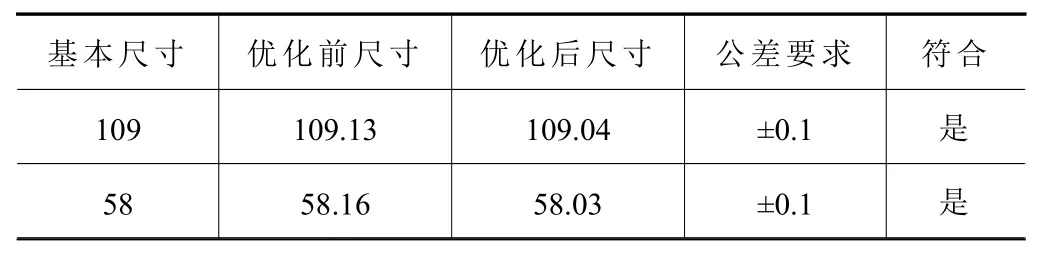
表4 檢測結果 mm

由表4可知，鋁合金薄壁殼零件尺寸相比優化前的尺寸均在公差要求范圍以內。

7 結語

通過Isight軟件平臺，本文提出了一種基于Kriging-MIGA算法的薄壁零件銑削參數優化方法。以6 061鋁合金薄壁殼零件為研究背景，搭建以銑削力最小為優化目標，主軸轉速、徑向切深和軸向切深為優化變量的多目標優化模型，采用了MIGA算法對模型尋優，分別將優化前后的銑削力數值進行對比分析，研究發現本文采用的優化方法有效地降低了銑削力，減小了薄壁件的變形量，為現場技術人員選擇合理的銑削參數提供了理論依據。