基于改進模糊Shapley值的“兩票制”醫藥冷鏈收益分配研究

葛嘉怡，高更君

（上海海事大學 物流科學與工程研究院，上海 201200）

0 引言

“兩票制”政策推動了醫藥供應鏈結構的調整和重組，對解決醫藥供應鏈條過長、耗占比高、過票洗錢等問題有著積極作用，但由于醫藥供應鏈重組的不穩定性導致供應鏈脫節現象時有發生，尤其對作業時間與環節以及服務條件有著嚴格要求的醫藥冷鏈，而參與企業收益合理分配的公平與否直接影響著醫藥冷鏈運行的穩定性和可靠性[1，2]。探究合理的收益分配策略，維護醫藥冷鏈公平穩定，對于提升醫藥冷鏈作業效率，提高醫藥冷鏈敏捷性，提高醫療機構銷量，擴寬醫藥冷鏈整體收益有著重要意義。因此，如何設計公平的收益分配策略成為醫藥冷鏈亟需解決的問題。

目前國內外有關醫藥冷鏈利益分配問題的研究偏少，但對供應鏈利益分配問題已有很多學者研究和關注，區別在于供應鏈構成不同、研究方法不同。現有利益分配方法主要集中在Nash 談判模型、MRCS法、最小核心法和Shapley法[3]，其中Shapley法在解決利益分配時可以較好的兼顧“公平”和“效率”，有效調動企業的積極性，且計算方法單調，具有可操作性，但改方法應用到實際生活中還存在一定的缺陷，即假設參與成員完全投入、完全不投入到某一個聯盟中，不存在以一定參與度投入到某一個聯盟中，且該成員在參與聯盟前完全知道整體收益和個人所得收益。為了更好的解決利益分配問題，Aubin[4，5]提出了模糊聯盟，定義了局中人以[0，1]的模糊參與度加入合作，但該假設的前提是支付函數為確定值。Butnariu[6]在Aubin研究的基礎上提出了模糊Shapley函數，該函數不連續且不單調非，不適用實際問題。Mears[7]提出了模糊Shapley值，并給出了Shapley值的“隸屬函數”，但該方法無法滿足Shapley值的三條公理，沒有確定利益分配的結果。由于參與度或支付函數的不確定性，無法采用確定值預估整個合作的收益分配，潘華[8]提出三角模糊函數確定模糊量的取值范圍，通過模糊量取值范圍的概率來確定最終值，來解決模糊不確定問題。本文基于以上研究，引入模糊支付合作對策，定義了具有三角模糊函數支付合作對策和模糊Shapley值，證明了該方法滿足經典Shapley值的三條公理，使支付模糊但聯盟清晰的假設更符合實際情況，并結合“兩票制”醫藥冷鏈收益分配的影響因素，采用熵值法、序關系分析法和Topsis法確定綜合影響系數，構建了改進模糊Shapley值模型，可以更好的保證利益分配的公平性，促進醫藥冷鏈參與成員合作的積極性和穩固性。

1 “兩票制”醫藥冷鏈收益分配影響因素分析

在“兩票制”醫藥冷鏈中，醫藥生產企業根據流通企業的需求生產藥品，并在嚴格的溫控環境下將藥品運輸到流通企業；流通企業負責藥品的存儲和銷售，再根據訂貨需求將藥品配送至醫療機構；醫療機構根據患者需求將藥品發放到各個藥房。“兩票制”下醫藥冷鏈運行模式如圖1所示。

圖1 “兩票制”下醫藥冷鏈運行模式

1.1 設備投入

投入指企業用于運營中的商品或者勞務，貨車長距離運輸、藥品種類繁雜、運輸環境嚴格苛刻，對作業設備有很高的要求，同時醫藥冷鏈的規模通常由藥品流通量決定，而承擔這一切的正是醫藥冷鏈設備的投入，因此設備投入是評價醫藥冷鏈收益分配的一個重要因素。

1.2 努力水平

努力水平是指各參與企業為完成作業而采取積極措施的程度，醫藥冷鏈參與成員的努力程度與市場需求也具有一定的相關性[9]，參與企業管理目標、行為表現不同，合作態度也不同，積極的態度必然增加醫藥冷鏈的收益[10]。因此，努力水平作為收益分配的影響因素可以有效避免參與企業消極的合作行為。

1.3 風險承擔

在醫藥冷鏈合作的過程中，參與企業要面對斷鏈風險、時間風險、能力風險、藥品污染風險等，這些風險直接影響參與企業的運營，導致市場份額的降低，為了體現合作的收益共享、風險共擔，參與企業承擔的風險越大，其所得收益分配也相應增加。因此，風險承擔是影響醫藥冷鏈收益分配的重要因子。

2 改進模糊Shapley值的收益分配模型構建

2.1 模糊支付合作對策和模糊Shapley值

定義1[11]令R 為實數集，若=(v1，v2，v3)，且v1≤v2≤v3，稱為三角模糊數，則其隸屬度函數(x)：

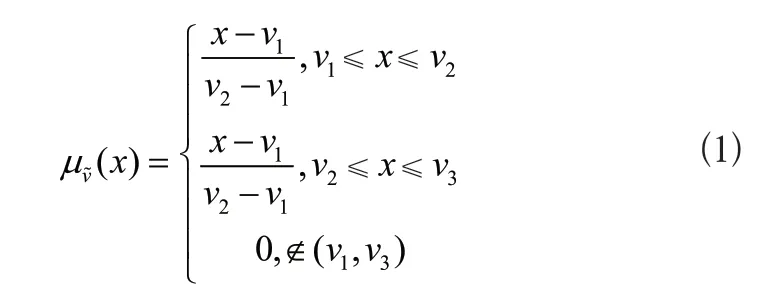
2.2 模糊Shapley值的隸屬函數

“兩票制”醫藥冷鏈是具有n人合作對策的收益分配問題，本文建立的模糊Shapley值模型需要借助“隸屬函數”來確定收益分配方案。不同截集上的Shapley值左右端點分別記為，將左右端點間區間組成集合套，即可得到模糊Shapley 值的隸屬函數。

2.3 改進模糊Shapley值的醫藥冷鏈收益分配模型

模糊Shapley值模型只考慮了各企業對醫藥冷鏈的效益所做貢獻大小，按照各企業對合作中的邊際貢獻決定各自的收益分配額。模糊Shapley值法計算的前提是各參與企業關系平等，即忽略了各企業間接導致收益增減的行為，無法保證收益公平。參與企業在設施設備投入、努力水平以及承擔風險都會不同，這些因素構成了參與企業在醫藥冷鏈收益分配上的議價能力。因此在醫藥冷鏈收益分配中，要考慮上述影響因素對收益分配模糊Shapley值進行修正。

在“兩票制”醫藥冷鏈合作項目中，不考慮影響因素的情況下，各參與企業對收益分配影響是均等的，記為1/n，考慮影響因素下，參與成員i的影響系數為，且，則Σ修正系數為。則改進模糊Shapley值模型為：

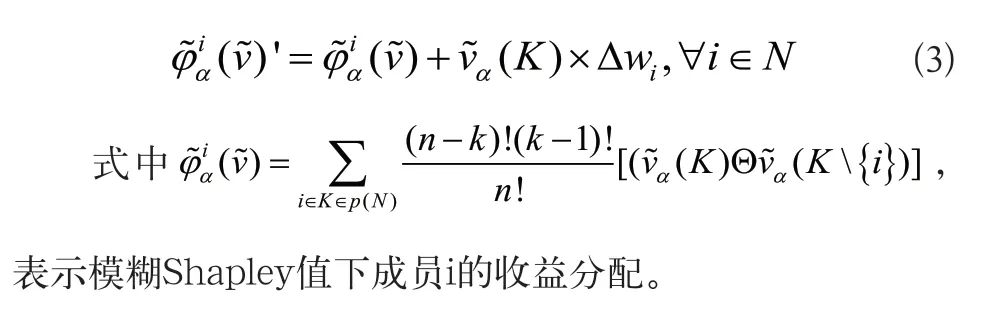
3 模型求解

1）熵值法確定收益分配影響因素權重

在協同集聚路徑的中介作用檢驗方面，由模型11可知文化與旅游業融合能對產業協同集聚產生顯著正向影響；同時，模型12中文化與旅游產業融合的估計系數也小于基準模型3中的系數值，意味著協同集聚路徑發揮了部分中介作用，理論假說3獲得支持。但值得深思的是，中介效應僅占總效應的3%，表明文化與旅游業融合借助協同集聚效應來促進旅游產業升級的作用程度較為有限，這也側面印證了我國文化與旅游產業的協同集聚度較低，Jacobs外部性收益尚未充分釋放。

通過各參與企業對各影響因素的定量分析，將各個指標的測度值進行標準化處理得到判斷矩陣R=(rji)n×m，采用熵值法確定各影響因素θ下參與企業的權重為：

上式中，rji表示各指標測度值歸一化后的數據，pji表示歸一化測度值rji處于i類指標的概率，Ei表示各指標的信息熵。

2）序關系分析法確定各影響因素間相對系數

建立收益分配影響因素集合X={X1，X2，…，Xm}，根據各指標的重要性，確定指標的排列順序，若Xi比Xk重要，則表示為Xi＞Xk。專家關于評價指標Xk-1和Xk的相對重要程度之比為rk，rk賦值如表1所示[15]。運用序關系分析法確定各影響因素相對權重。

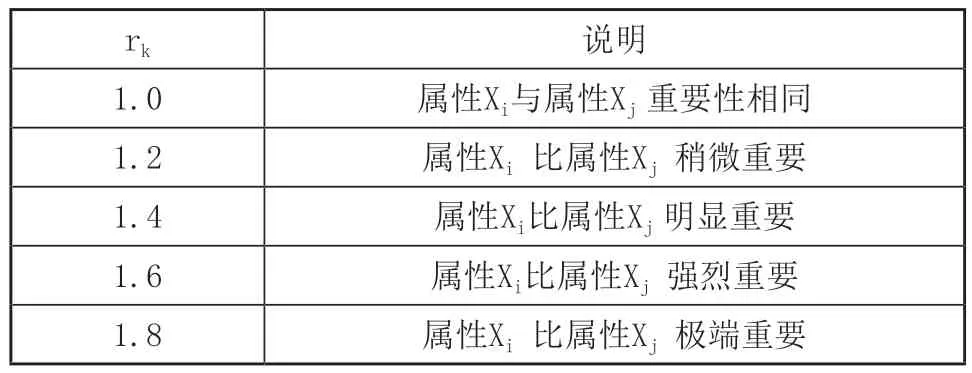
表1 屬性比較判斷表

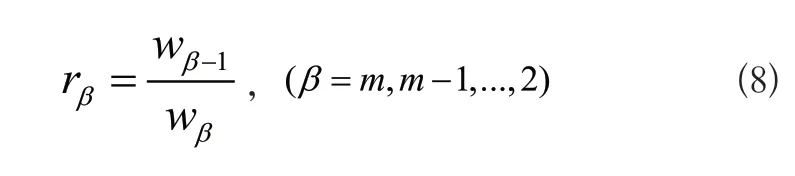
3）TOPSIS法確定各參與成員的修正系數通過各影響因素的相對權重wzβ和各影響因素下各參與企業的權重系數構建系數矩陣A。對A矩陣進行標準化處理得到矩陣B=(bij)n×m，確定絕對理想解與負理想解：

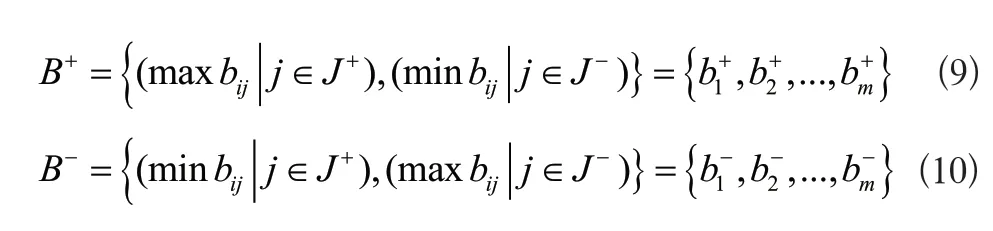
其中J+∪J-=J，J+表示數值愈大愈好的指標集合，J-表示數值愈大愈差的指標集合。本文選取1和0作為正向指標的絕對正理想值與絕對負理想值[16]。

確定各參與企業到正負理想點的歐幾里得距離：

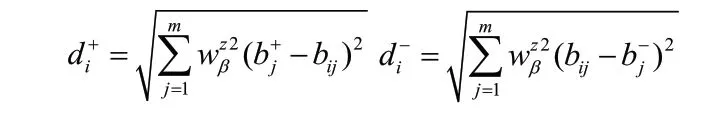
確定各參與企業與理想方案的接近程度，確定系數wi：

4 算例模擬

“兩票制”下的醫藥冷鏈由藥品生產企業A，藥品流通企業B，醫療機構C構成，各參與企業運營情況：生產企業A擁有2400m3冷庫容量，6量冷藏車，30臺冰箱，每月業務量180噸，任務執行度95%，科研人員30人，藥品斷鏈率2%，設備故障率2%，藥品損耗率4%；藥品流通企業B擁有2600m3冷庫容量，5量冷藏車，40臺冰箱，每月業務量180噸，任務執行度95%，科研人員8人，藥品斷鏈率3%，設備故障率5%，藥品損耗率6%；醫療機構C擁有1800m3冷庫容量，3量冷藏車，20臺冰箱，每月業務量150噸，任務執行度90%，科研人員20人，藥品斷鏈率4%，設備故障率5%，藥品損耗率7%。已知企業A、B、C單獨運營的利潤為[45，65]萬元；A、B合作利潤為[305，385]萬元，B、C合作利潤為[235，275]萬元，A、C合作利潤為[155，235]萬元，A、B、C合作運營的利潤[455，555]萬元。

各聯盟組合下的三角隸屬度函數μ v～(x)如下：

以0.2為步幅寬度在[0，1]區間改變置信水平α，得三角模糊支付函數α截集如表2所示。

表2 三角模糊支付函數α截集

通過(1)式計算不同置信水平α上Shapley值取值范圍：

表3 不同置信度下的區間模糊Shapley值

醫藥生產企業A，假設他希望決策具有較高的可靠性，選取置信水平α=0.8，且認為所得收益是區域上限，即203.33 萬元，則利益分配方案為φα=0.8=[203.33，179.33，132.33]，醫藥流通企業B和醫療機構C經過同樣的思想過程后，都會選擇該方案。根據式(4)～式(11)求解各參與企業在不同影響因素下的權重如表4所示。

表4 綜合影響因子

比較置信水平α=0.8下模糊Shapley值改進前后醫藥冷鏈利益分配結果如表5所示。

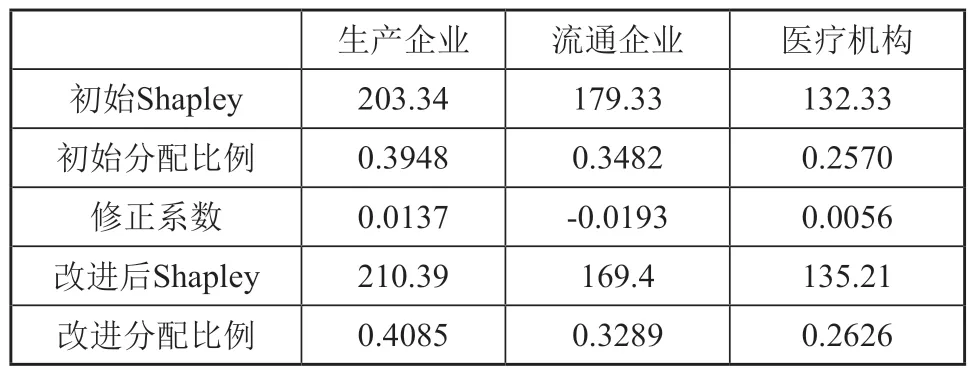
表5 模糊Shapley值改進前后的利益分配

由表5數據可以看出Shapley值改進前后各企業的收益值有明顯差異。生產企業和醫療機構的收益都有一定幅度的增長，而流通企業的收益則相對減少，這是由于生產企業與流通企業在設備投入和風險承擔上均有良好表現，在努力水平上又處于均值，所以綜合影響因素Δw1=0.0137＞0，Δw3=0.0056＞0應獲得相應的補償。流通企業在設備投入、努力水平和風險承擔上表現較差，沒有達到平均水平，故綜合影響因素系數Δw1=0.0193＞0，應獲得懲罰。貢獻度高的企業將分得更多收益，符合高投入高回報原則[17]，該分配結果不僅提高了“兩票制”下醫藥冷鏈收益分配的公平性，還促進了醫藥冷鏈合作的積極性和穩固性。

5 結語

本文研究了“兩票制”醫藥冷鏈收益分配問題，考慮到實際生活中合作收益的不確定性，提出了三角模糊支付合作對策和模糊Shapley值。考慮到投入因素、風險因素、努力水平對收益分配的影響，采用熵值法、序關系分析法、Topsis法相結合確定影響因素系數，改進模糊Shapley值收益分配模型。結果表明，三角模糊支付函數更符合實際生活中的合作情況，改進后的模糊Shapley值可以更好解決醫藥冷鏈的收益分配問題，各參與企業要想獲得更多的收益，必須在設備投入、風險承擔、努力水平等方面發揮更大的作用。