不完美SIC 下NOMA 系統用戶配對和功率分配聯合優化*

陳 程，李 燁

（上海理工大學 光電信息與計算機工程學院，上海 200093）

0 引言

非正交多址[1]（Non-Orthogonal Multiple Access，NOMA）技術是在正交頻分多址接入（Orthogonal Frequency Division Multiple Access，OFDMA） 技術的基礎上引入功率域的概念，以增加接收端復雜度的代價來提升系統的吞吐量性能[2]。NOMA系統主要依靠在發送端對用戶信號進行疊加編碼（Superposition Coding，SC）和在接收端使用串行干擾消除（Successive Interference Cancellation，SIC）技術恢復原始用戶信號[3]。由于NOMA 系統最大化系統和速率問題是一個非線性混合整數規劃問題[4]，需要同時考慮用戶配對和功率分配對系統和速率的影響，但這種求解方式復雜度較高。因此，大多數研究只是從用戶配對或功率分配其中一個角度對系統和速率進行優化。

在用戶配對方面，一般是將具有較大信道增益差的用戶進行配對[5]。Islam 等人[6]提出最大-最小信道增益用戶配對，這樣的配對方式存在近零問題，導致系統和速率降低。Mounchili 等人[7]提出了分布式NOMA（Distributed NOMA，D-NOMA）配對算法，保證配對用戶間存在最小信道增益差。Mounchili 等人[8]還提出了一種最小距離（Minimum Distance NOMA，MD-NOMA）配對算法，推導出參與配對用戶的增益差閉式表達式。相比于規則量化的配對算法，基于啟發式的配對搜索算法如爬山算法[9]、模擬退火算法[9]、匈牙利算法[10]、粒子群算法[11]、神經網絡[12]等也被應用于用戶配對問題中。

在功率分配方面，Fu 等人[13]提出了改進注水功率分配算法；Tong 等人[14]提出了復數域的功率分配方法；Mounchili 等人[8]推導出滿足用戶服務質量（Quantity of Service，QoS）的功率分配系數閉式解；Gupta 等人[15]從能量效率角度提出了基于Dinklebach 的迭代功率分配算法；Lee 等人[16]提出了基于強化學習的功率分配算法；Huang 等人[17]從和速率、能量效率角度，以及Fathimath Shamna 等人[18]從用戶公平性的角度，結合深度學習對功率分配問題進行研究。

然而，上述研究都是單獨考慮用戶配對或功率分配問題，實際上用戶配對方案和功率分配方案互為條件，對系統和速率均有著重要的影響。同時，這些研究都是基于接收端能完美執行SIC 的假設，但由于接收端硬件處理能力不足、信號重構異步等因素[19]，接收端會存在干擾殘留，導致系統和速率降低。本文基于接收端不完美執行SIC 的假設，提出一種用戶配對和功率分配聯合優化（Joint optimization of User Pairing and Power Allocation，JUPPA）算法。

1 系統模型

考慮單基站蜂窩下行NOMA 系統的L個用戶均勻分布在半徑為R的小區中，形成M個用戶對，每個用戶對中有N個用戶（M≤L/N），相同用戶對內的用戶在同一資源塊上復用。系統總帶寬為B，用戶對帶寬為Bw。

假設基站側已知用戶信道狀態信息（Channel State Information，CSI），且信道增益滿足其中，hi,l為基站到用戶對l中用戶i的信道矩陣；ωl為預編碼矩陣。定義用戶對中信道增益較大者為強用戶，信道增益較小者為弱用戶。

如圖1 所示，按照NOMA 系統工作原理，基站采用疊加編碼技術發射信號并進行功率控制，信道增益越大的用戶，基站分配的功率越低。在接收端，用戶根據串行干擾消除原則恢復信號，將信道增益較大的用戶視為干擾，依次濾波解碼信道增益較小的用戶并進行信號重構，移除該重構信號后，順序解調恢復其他用戶信號。

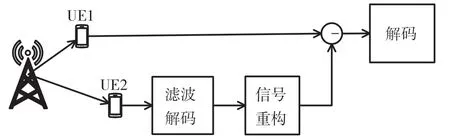
圖1 單基站蜂窩下行NOMA 系統

在傳統NOMA 系統中，經過發射端的信號疊加和接收端的串行干擾消除，接收端用戶信干噪比（Signal to Interference plus Noise Ratio，SINR）為：

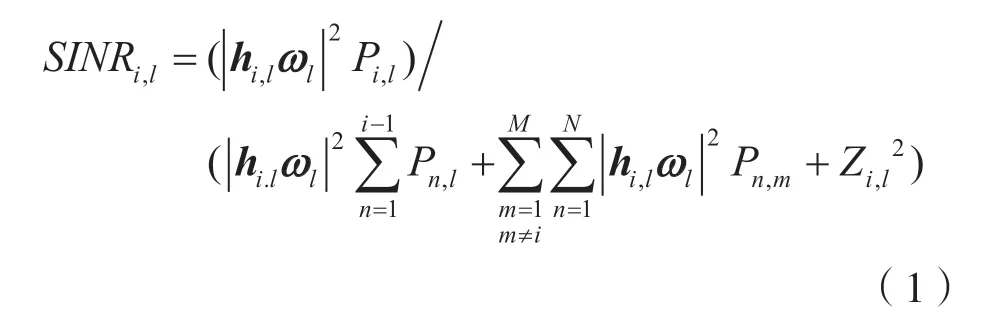
式中：Pi,l為用戶對l中用戶i的功率；分子為目標用戶信號功率；分母中第1 項為用戶對l中其他用戶的干擾信號功率，第2 項為不同用戶對對間干擾；Zi,l～CN(0,1)為高斯白噪聲。

受接收端硬件處理能力不足和信號重構異步等因素影響，實際接收端并不能完美執行SIC，因此用戶的接收信號中還存在已解調用戶的殘余信號，則接收端不能完美執行SIC 時，目標用戶SINR 為：

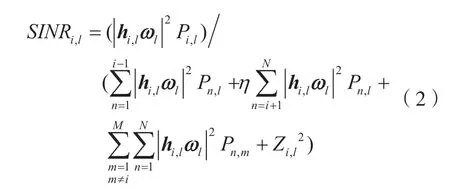
式中：η為不完美SIC 系數且η∈[0,1]，η=0 表示接收端執行完美SIC，η=1 表示接收端不能執行SIC。

對于對間干擾，可以采用迫零波束賦形[20]設計的預編碼矩陣消除，則目標用戶的SINR 為：

根據香農公式，NOMA 系統最大和速率優化問題為：

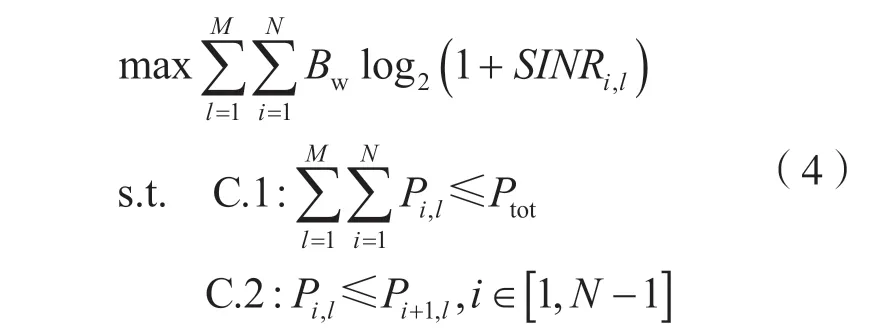
式中：Ptot為基站總發射功率；約束C.1 確保小區內用戶分配的總功率小于系統總發射功率；約束C.2確保用戶對中弱用戶分配到的功率比強用戶分配到的功率大。若用戶配對方法已知，優化問題轉化為求解最優功率分配矩陣問題；若功率分配矩陣已知，則轉化為求解最優用戶配對方案問題。但這兩種情形下得到的均為非全局最優解。

2 用戶配對和功率分配聯合優化算法

考慮到用戶配對問題的實質為組合優化問題，可用局部搜索算法求解，而功率分配問題為非凸問題，用連續凸逼近（Successive Convex Approximation，SCA）算法求解復雜度低，且其收斂結果與對應卡羅需庫恩塔克（Karush-Kuhn-Tucker，KKT）條件極值點相同[21]，提出JUPPA 算法，算法流程如圖2所示。基于自適應遺傳算法（Adaptive Genetic Algorithm，AGA）進行用戶配對方案搜索，對AGA 算法中的每一個用戶配對方案根據SCA 準則[22]和KKT 條件[22]進行功率分配優化，用尋優得到的功率分配系數矩陣計算適應度值，并依據計算得到的適應度值進行下一代種群的選擇、交叉和變異。交替進行用戶配對方案尋優和功率分配方案尋優，直至系統和速率收斂。

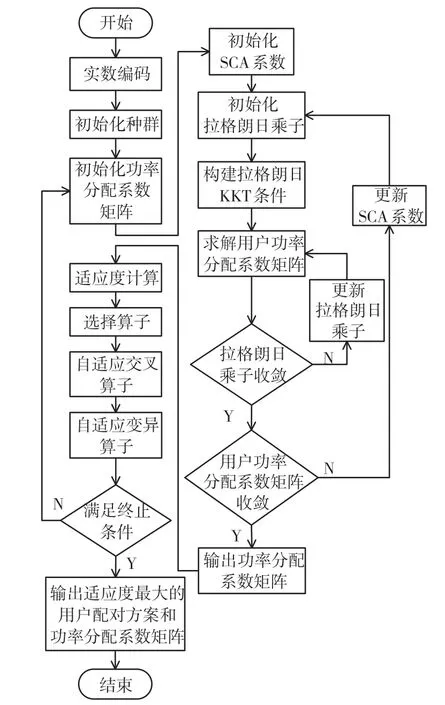
圖2 用戶配對和功率分配聯合優化算法

2.1 用戶配對

常規遺傳算法（Genetic Algorithm，GA）[23,24]實現簡單，但是容易陷入局部最優，并且設置交叉、變異概率過大會導致算法變成隨機搜索，而設置交叉、變異概率過小會導致算法收斂過慢。針對常規GA 算法的不足，采用如圖2 所示的AGA 算法進行用戶配對方案搜索。使用自適應交叉和變異算子，根據種群適應度，自適應地調節交叉、變異概率，使算法更好地達到全局最優。同時，在交叉、變異生成新種群的過程中引入哈希表，避免產生重復的個體，提高算法的搜索效率。

2.1.1 編碼策略

選用實數編碼策略，便于直接在用戶配對方案的表現型上進行交叉、變異操作。按照用戶的生成順序依次對用戶進行編碼，小區內用戶的數量L即染色體的長度。

2.1.2 初始化種群

初始種群由Pop個長度為L的不重復染色體序列組成。按照染色體中基因序列的前后順序，連續N個基因表示一個用戶對，共組成M（M=L/N）個用戶對，即形成一種用戶配對方案。

2.1.3 選擇算子

基于輪盤賭策略選擇下一代種群中的父代，計算個體的適應度值在當前種群適應度的占比，即個體被選中作為父代的概率大小。適應度越高的個體，被選中作為父代的概率越大。

2.1.4 自適應交叉算子

從父代中隨機選擇兩個染色體進行兩點交叉，為了確保染色體中每個基因僅出現一次，對交叉后的染色體進行沖突檢測，交叉概率隨種群適應度值自適應變化，其表達式為：

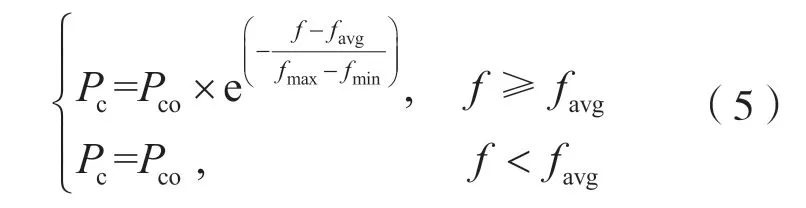
式中：fmax為當代種群中最大適應度值；fmin為當代種群中最小適應度值；favg為當代種群中平均適應度值；f為進行交叉操作的個體中較大適應度值；Pco為初始交叉概率；Pc為自適應變化的交叉概率。

2.1.5 自適應變異算子

在染色體內隨機選擇一個基因進行單點變異，即在染色體中隨機選擇兩個基因交換。變異概率隨種群適應度值的變化而變化，其表達式為：

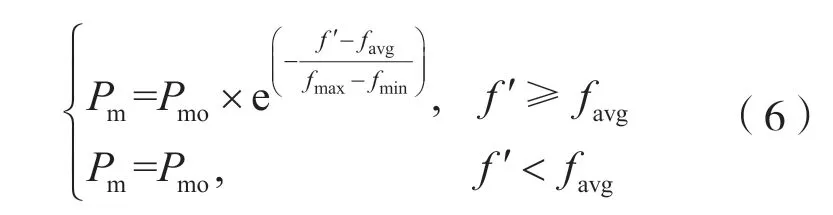
式中：Pmo為初始變異概率；Pm為自適應變化的變異概率；f′為進行變異操作的個體的適應度值。

2.1.6 適應度計算

對于每個染色體，根據染色體表示的用戶配對方案，結合當前的用戶功率分配矩陣，計算系統和速率，作為其適應度值。

2.2 功率分配

最大化系統和速率是一個非凸混合整數規劃問題[4]，直接求解復雜度會隨著約束條件和變量數呈指數增長。因此，通過拉格朗日乘子法和SCA 算法[21,22,25]求解最優功率分配系數矩陣。首先，使用SCA 算法對目標函數做凸處理；其次，使用拉格朗日乘子法構造KKT 條件，將有約束問題轉化為無約束問題；最后，通過梯度下降法更新拉格朗日乘子。由收斂的拉格朗日乘子求解用戶功率，用解得的用戶功率進一步更新SCA 系數，直到拉格朗日乘子和用戶功率同時收斂。

2.2.1 系統模型凸逼近

通過連續凸逼近方法，以原目標函數下界構造替代函數：

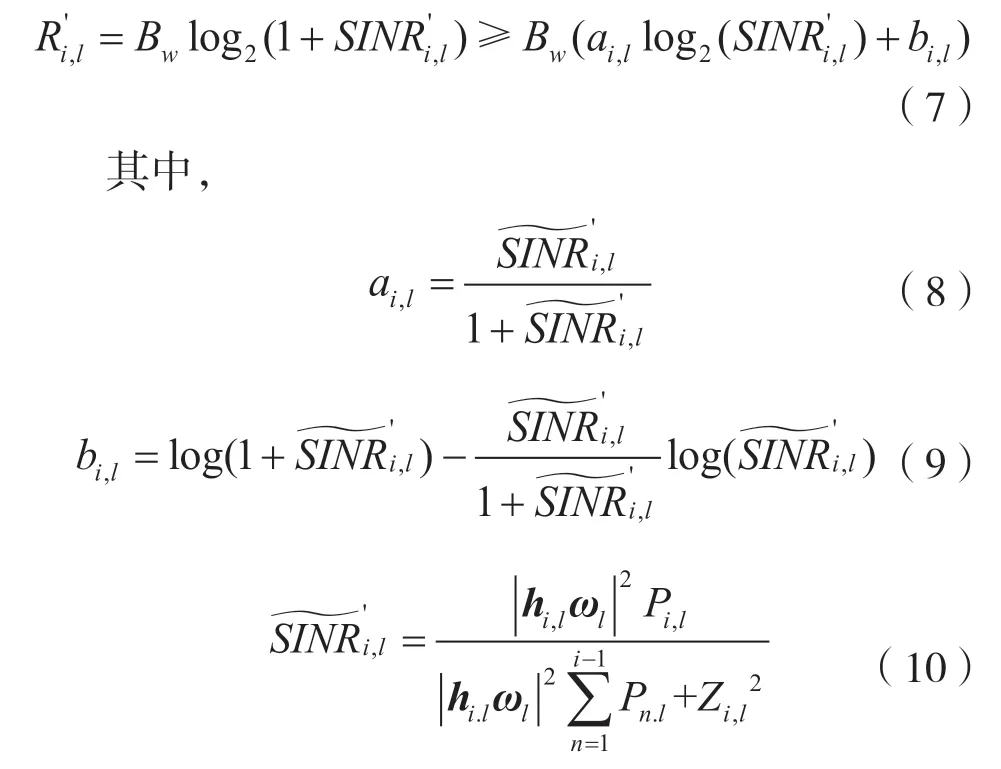
式中：R′i,l為用戶對l中用戶i的系統速率；a,b為SCA 系數；為輔助變量；SINR′i,l取最后一次迭代值。

這樣，優化問題轉換為：

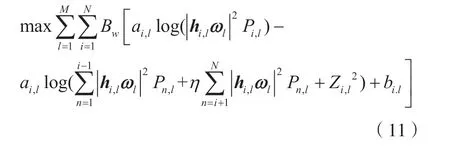
2.2.2 構建拉格朗日KKT 條件

由于式（11）目標函數仍為非凸函數，令Pi,l=eμi,l，將其轉換為log-sum-exp 形式，可得：

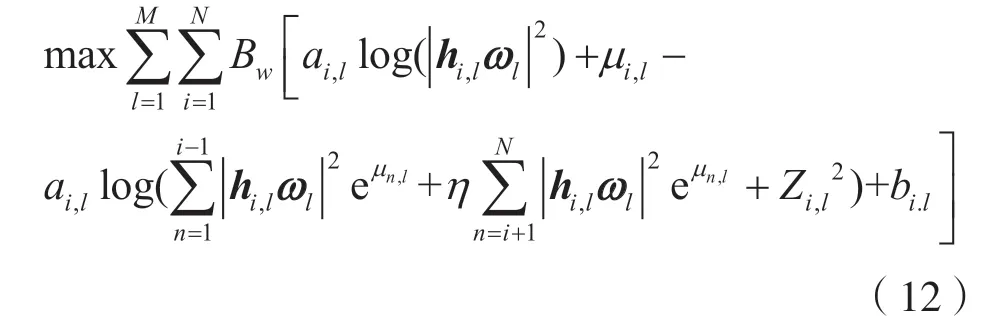
式中：μi,l為用戶對l中用戶i的功率值所對應的指數次方項。

同時，由于log-sum-exp 為凸函數[26]，而約束條件也為凸函數，因此可以通過構造拉格朗日KKT條件來求解。

引入拉格朗日乘子v和ξi,l，將有約束問題轉化為如下無約束求極值問題，即可求得用戶功率。

對于拉格朗日乘子，采用梯度下降法進行迭代更新：

式中：t為迭代次數；φ和ψ為步長。功率分配算法的具體偽代碼如下：

3 系統仿真

3.1 仿真參數設置

通過實驗仿真對所提算法性能進行驗證。在以基站為中心，半徑為500 m 的蜂窩范圍內生成隨機獨立分布的終端用戶，設定用戶數L=16。以NOMA方式進行用戶復用，設定功率域疊加用戶數N=2。無線信道為獨立均勻分布的瑞利衰落信道。仿真參數設置如表1 所示。

表1 仿真參數

3.2 仿真實驗

3.2.1 不完美SIC 系數影響分析

為了研究不同程度干擾殘留即接收端執行SIC能力對系統和速率的影響，設置不同的干擾殘余系數η對JUPPA 算法進行仿真實驗，結果如圖3 所示。η=0 表示接收端執行完美SIC，即接收端不存在干擾殘留，此時系統和速率最高。在用戶信噪比相同的情況下，隨著干擾系數的增加，系統和速率持續下降。這是由于在NOMA 系統中，干擾殘余系數不會對弱用戶的速率造成影響，但是強用戶的SINR會隨著干擾系數的增大而減小，導致強用戶的速率降低，進而造成系統和速率下降。同時，當用戶信噪比由10 dB 增加到40 dB，在η=0 時，系統有約10.5 Mbit/s 的和速率提升；η=0.01 時，系統和速率僅有約5.5 Mbit/s 的提升，說明當接收端存在干擾殘留時，增大用戶信噪比帶來的和速率增益也會下降。當接收端執行串行干擾消除能力持續下降即干擾殘留系數越來越大時，相比于正交多址接入（Orthogonal Multiple Access，OMA）系統，NOMA系統并不會帶來系統和速率上的增益。當η=0.5 時，NOMA 系統和速率已明顯低于OMA 系統和速率。

圖3 不完美SIC 系數對系統和速率的影響

3.2.2 自適應遺傳算法性能分析

將JUPPA 算法與常規GA 算法[24]和AGA 算法進行對比研究，仿真結果如圖4 所示。可以看出，當接收端干擾殘留系數相同，且GA 算法和AGA 算法使用相同功率分配算法時，兩種算法均能求得最優的用戶配對方案，達到基本一致的系統和速率性能。對比JUPPA 算法和AGA 算法，在使用相同用戶配對算法的情況下，JUPPA 算法具有更高的系統和速率，說明在JUPPA 算法中，所提功率分配方案能帶來更大的系統和速率增益。

圖4 JUPPA 算法、常規GA 算法和AGA 算法對比

然而，由圖5 常規GA 算法和AGA 算法收斂對比可知，在基站發射功率、干擾殘留系數相同的情況下，常規GA 算法在24 輪迭代后收斂，而AGA 算法在15 輪迭代即已接近于GA 算法收斂值，其后的和速率性能一直優于常規GA 算法。此外，22 輪之后的迭代，展現了AGA 算法跳出局部最優的強大能力。

圖5 常規GA 算法和AGA 算法收斂性對比

3.2.3 與典型功率分配算法對比

將JUPPA 算法與當前代表性的功率分配算法，即固定功率分配（Fixed Power Allocation，FPA）算法[19]和分數階功率分配（Fractional Transmit Power Allocation，FTPA）算法[10]進行對比研究，仿真結果如圖6 所示。顯然，在用戶信噪比、干擾殘余系數和用戶配對方式均相同的情況下，JUPPA 算法具有更高的系統和速率，這是由于FPA 算法和FTPA算法僅按照信道增益進行功率分配。相比之下，JUPPA 算法考慮了干擾殘留系數對系統和速率的影響，在確保NOMA 系統用戶對中強弱用戶功率分配原則下，干擾系數越大，會分配越多的功率給弱用戶，由弱用戶帶來系統和速率上的提升。對比FPA算法和FTPA 算法，在用戶配對方案相同的情況下，由于FTPA 算法能夠動態地適應用戶對中用戶信道增益的變化，調整強弱用戶之間的功率分配權重，因此FTPA 算法具有更高的系統和速率。

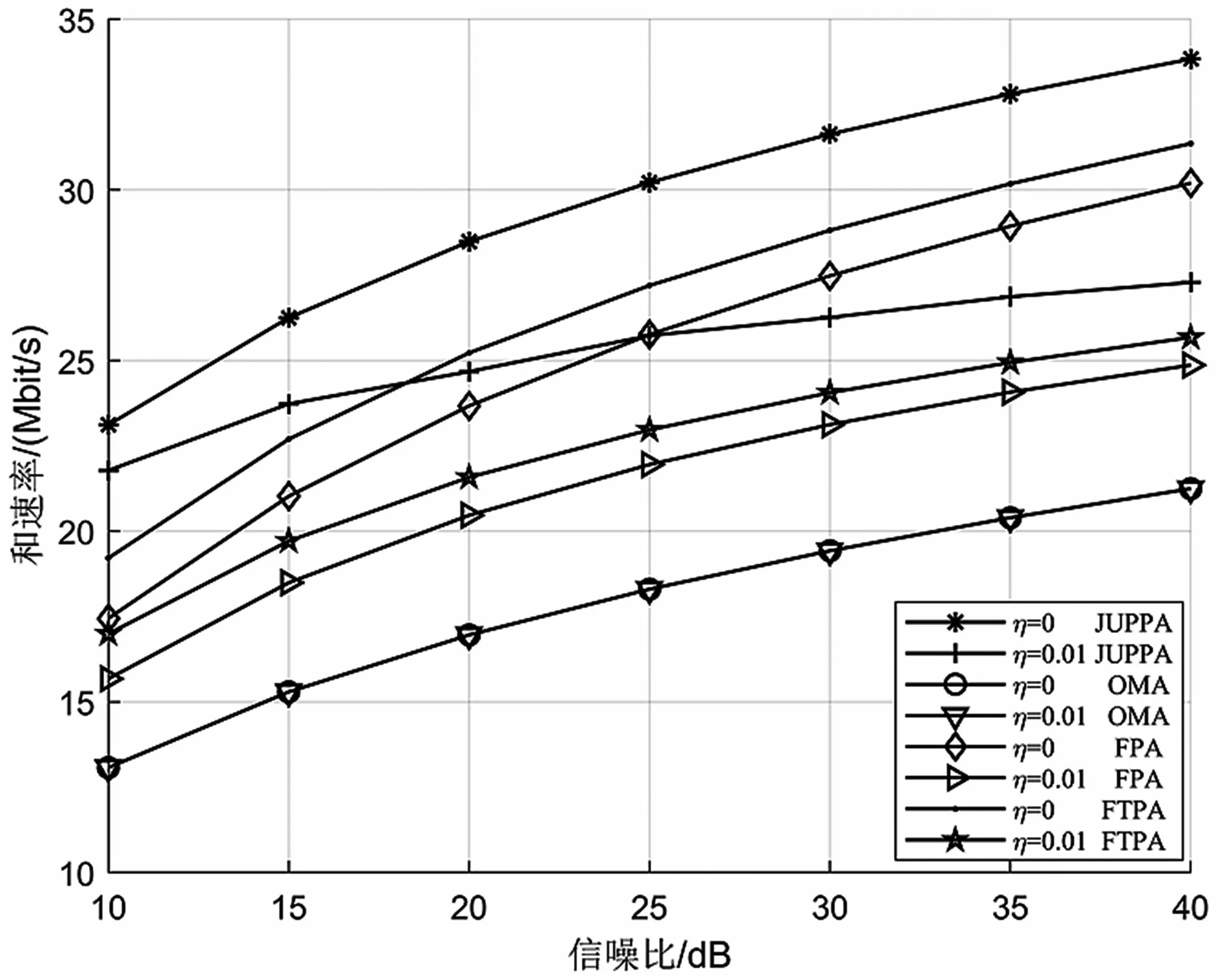
圖6 JUPPA 算法與典型功率分配算法對比

3.2.4 與典型功率分配算法對比

將JUPPA 和代表性的用戶配對算法，即隨機用戶配對（Random Pairing Algorithm，RPA）算法[3]和基于最大信道增益差的傳統NOMA 配對（Conventional NOMA，C-NOMA）算法[7]進行對比研究，仿真結果如圖7 所示。可見，相同功率分配算法下，JUPPA 算法擁有比RPA 算法和C-NOMA算法更高的系統和速率。這是由于JUPPA 算法使用AGA 算法在用戶配對組合方案中進行搜索，而RPA 算法未考慮用戶之間信道增益差異，C-NOMA算法則未考慮用戶間的信道增益近零問題。RPA 算法的和速率性能僅優于OMA 系統，因為在NOMA系統中將具有一定信道增益差的用戶進行配對就能產生一定的系統和速率增益，使得NOMA 系統的和速率優于OMA 系統。同樣，對比不同干擾殘留系數下的OMA 系統和速率，由于OMA 系統不存在功率域的復用，即不涉及用戶配對，也就并不存在干擾殘留的問題，故不同干擾殘留系數的OMA 系統和速率曲線完全一致。

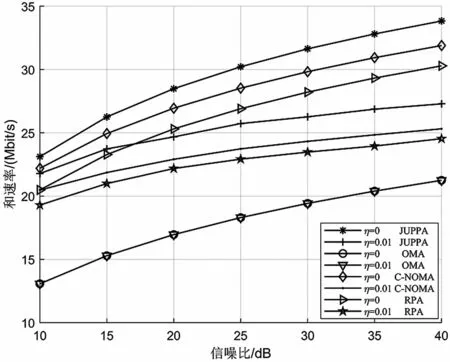
圖7 JUPPA 算法與典型用戶配對算法對比

4 結語

本文針對不完美SIC 下的NOMA 系統和速率優化問題，提出了一種聯合用戶配對和功率分配的優化算法JUPPA。在用戶配對階段，設計了AGA 算法進行用戶配對方案尋優；在功率分配階段，采用SCA 準則和KKT 條件求解最優功率分配系數矩陣。仿真結果表明，接收端執行SIC 的能力強弱，對系統和速率有著較大影響，同時，JUPPA 算法中AGA算法相比常規GA 算法具有更高的收斂速度和更優的全局搜索能力，且與已有用戶配對和功率分配算法對比，JUPPA 算法具有更高的系統和速率。對于考慮不完美SIC 的NOMA 系統研究，本文具有一定的參考意義。