底面局部加熱條件下熱湍流的流場變化及傳熱規律

胡 瑾，章盛祺，夏振華，*

(1. 浙江大學 流體動力與機電系統國家重點實驗室，杭州 310027；2. 浙江大學 航空航天學院，杭州 310027；3. 南方科技大學 廣東省湍流基礎研究與應用重點實驗室，深圳 518055；4. 北京大學 湍流與復雜系統國家重點實驗室，北京 100871)

0 引 言

熱對流是一種常見的物理現象，與人們的日常生活、生產息息相關[1]。其不僅存在于北極夏季融冰湖[2]、大氣及海洋環流[3-4]、地球內部地幔形成[5]等自然現象中；還廣泛應用于核反應堆冷卻[6]、新型儲能材料[7]、芯片散熱[8]、磁流體傳熱[9]等工業工程問題中。而Rayleigh-Bénard對流（Rayleigh-Bénard convection，RBC）系統，則是從眾多復雜的自然現象及工程問題中抽象簡化出來的研究對流問題的經典模型。同時，由于RBC系統中可以同時存在多種熱量傳遞方式，因此它也是傳熱領域非常經典的課題，研究RBC系統對認識實際情況下各種各樣對流過程中的傳熱機制有著非常重要的意義。

狹義上的RBC通常指在一個封閉腔體內，上表面冷卻，下表面加熱，形成恒定溫差，從而導致腔體內流體產生特殊流動的系統，如圖1（來源van der Poel等[10]）所示。當系統充分發展后，上下壁面附近會形成溫度邊界層[11]，同時不斷生成冷熱羽流，并在腔體中形成穩定的大尺度環流（large-scale circulation，LSC）結構。除了對經典標度律[12-15]、擬序結構[16-17]及能量耗散[18-19]等的研究，科研工作者在近二十年對LSC的反轉問題也進行了深入的研究[20-22]。最近Jiang等[23]通過設置上下壁面的非對稱棘輪狀粗糙度和引入較小傾角對熱對流系統中的LSC和傳熱進行控制；Zhang等[24-25]通過增加側壁局部恒溫條件也實現了對LSC反轉及強弱的有效控制。

圖1 RBC系統示意圖[10]Fig. 1 Sketch of RBC system[10]

由于經典的RBC系統假設上下邊界溫度恒定且分布均勻，這與一些實際系統的熱邊界條件并不相符。例如在地球物理研究中模擬地幔對流時，需要考慮熱傳導性差異較大的大陸板塊與海洋板塊，此時熱邊界條件就不再均勻。另一方面，工程應用中一些對流換熱優化問題也需要考慮非均勻熱邊界條件。在對流換熱的優化問題研究中，已有的增加對流傳熱效率的途徑主要分為兩種：一是改變換熱板表面的粗糙度，該方法已被證明可在有限Rayleigh數（Ra）范圍內顯著增強對流熱流[26-29]；二是采用等溫和絕熱相結合的混合熱邊界條件，已有的數值和實驗研究結果表明，系統的傳熱效率會隨絕熱面積的增大而減小[30]，當絕熱面積超過50%時不同的絕熱位置設置會對熱傳遞產生顯著差異[31]。除此之外，也有科研人員發現，在非均勻熱邊界條件下，當單個絕熱塊特征尺度與溫度邊界層厚度相近時，其Nusselt數（Nu）會與經典RBC系統相近[32-33]。近來，Vasiliev等[34]研究了Prandtl數Pr=6.46、Ra=1×107時僅下壁面局部加熱條件對方腔內熱湍流系統的流動結構及傳熱規律的影響，其發現加熱面積相同時，LSC及形態與加熱塊數有較強的關聯，傳熱效率隨加熱塊數的增加而增大；Nandukumar等[35]研究了Pr= 1時，上下壁面均為一半加熱一半冷卻條件下熱對流系統與經典RBC系統的關系，其發現此非均勻熱邊界條件在1×105＜Ra＜1×108時可明顯增加系統傳熱效率。由此可知，研究非均勻熱邊界條件下熱對流的流場及傳熱規律是更切合實際和富有價值的。

但目前已有文獻中非均勻熱邊界條件主要考慮簡單對稱分布情況，所以進一步研究非對稱分布的復雜熱邊界條件對高Rayleigh數熱湍流系統流動結構及傳熱規律的影響是必要的。本文參考Zhang等[24-25]算例設置，基于Pr=2、Ra=1×108的經典二維RBC系統，改變其下壁面加熱條件，初步研究了加熱長度為方腔邊長一半時，不同局部加熱位置對系統LSC結構和傳熱效率的影響。

1 控制方程及數值設置

1.1 控制方程

假設方腔高為H，滿足寬高比 Γ=1；u=(u,v)，其中u、v分別為水平方向及豎直方向速度分量；θ為溫度，θl和 θu分別為下壁面加熱區域及上壁面的恒定溫度； Δθ=θl?θu為 上下壁面溫差；給定運動黏度υ，熱擴散系數κ，導熱系數λ，重力加速度g，熱膨脹系數β；坐標原點定義在方腔左下角。引入特征速度（自由落體速度）特征時間T=H/U、特征長度H、特征溫度 Δθ，對控制方程進行無量綱化。假設系統滿足Boussinesq近似，則可得無量綱控制方程組：

其中Ra和Pr為RBC系統的無量綱控制參數，其定義如下：

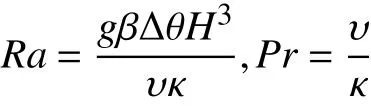
后文中變量如無特別說明，均已無量綱化。圖2為本文計算的三種局部加熱系統及RBC系統示意圖。左右壁面為絕熱條件，即 ?θ/?x= 0；上壁面恒溫冷卻，即 θ=0；下壁面非加熱區域滿足絕熱條件，即?θ/?y= 0，加熱區域滿足 θ=1。

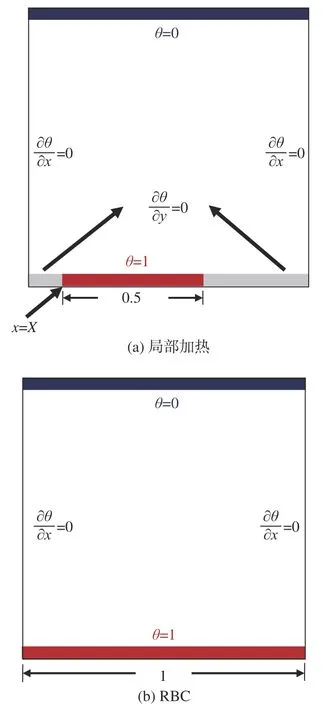
圖2 局部加熱系統及RBC系統計算示意圖Fig. 2 Sketches of local heating and RBC cases

1.2 數值方法

本文數值模擬均采用經過部分修改的二階有限差分法代碼AFiD[10]進行計算，其中離散Poisson方程通過水平方向的離散余弦變換解耦并采用三對角求解器進行求解，時間推進采用二階顯式Adams-Bashforth格式實現。與de Vahl Davis等[36]的方腔自然對流結果對比，文獻在Pr= 0.71、Ra= 1×104、1×105、1×106條件下的壁面時均Nu數為2.243、4.519、8.800，而本文所用程序計算的結果為2.256、4.537、8.839；與Zhang等[25]的經典RBC系統結果對比，文獻在Pr=2、Ra= 1×108條件下的壁面時均Nu數為24.90，而本文所用程序計算的結果為24.92。可以認為與已有文獻結果基本一致，證明了現有代碼的準確性。

1.3 算例設置

本文在Pr= 2、Ra= 1×108條件下，以加熱左端點無量綱坐標X為位置參數，對全局加熱（經典RBC）系統和局部加熱系統（加熱位置分別為X= 0、0.125、0.25，加熱長度l=0.5）進行統一的分析和比較。

所有算例中，水平方向為均勻網格，豎直方向為非均勻網格（靠近壁面處細化），保證邊界層內網格大小Δ＜0.6min[ηK,ηB][37]；時間步長足夠小，足以確保Courant-Friedrichs-Lewy數小于0.2；達到統計穩態后計算足夠長時間，RBC系統可觀察到反轉現象。文中 〈···〉表示對括號內變量求平均，下標表示如何平均。

2 計算結果及分析

2.1 局部加熱條件對流場變化的影響

首先考慮不同位置局部加熱條件對熱湍流達到統計穩態后的流動影響，分析總動能的時間演化情況。本文計算總動能為：

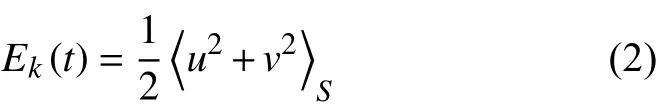
其中下角標S表示對整個計算域面積求平均。通過計算可得不同加熱位置及經典RBC的Ek(t)在達到統計穩態后的變化情況，如圖3所示。

圖3 不同加熱位置及經典RBC的Ek(t)變化情況Fig. 3 Time series of Ek(t) of local heating cases and traditional RBC case

其中RBC系統的總動能均值 〈Ek〉t=0.0200，最大值和最小值之間相差至少0.01，明顯比局部加熱系統的均值及振幅要大。但不同位置的局部加熱系統之間的均值差異并不明顯，因此我們進一步計算X=0、X=0.125、X=0.25三 個系統的 〈Ek〉t，可得其值分別為0.012 5、0.013 9、0.014 5，約 為RBC系統的62.5% ～72.5%。由于局部加熱系統三條曲線重合率較高，故由加熱位置從左至右分別給出系統Ek(t)的方差，結果為7.56×10?4、6.67×10?4、5.82×10?4，依次減小。綜上所述，我們可以認為，局部加熱系統中加熱位置越靠下壁面中心，系統總動能Ek(t)越大、其對應振幅越小。

根據前文所提，傳統RBC具有的流場結構特性之一便是當流動充分發展后，流場內會形成較為穩定的LSC結構且會發生反轉現象。為了分析局部加熱是否會影響LSC的反轉，本文采用角動量符號對此進行判斷。計算平均角動量定義如下[38]：

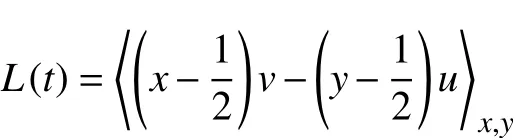
圖4給出局部加熱系統及RBC的L(t) 在1×104≤t≤4×104范圍內的演化情況，其中L<0表示LSC呈順時針狀態，L>0為逆時針。從圖4中可以明顯地看到經典RBC存在大渦反轉現象，而局部加熱系統均未出現反轉情況且LSC呈順時針狀態。放大局部加熱系統的L(t)演化情況，如圖5所示。結合圖5，進一步計算局部加熱系統達到統計穩態后角動量均值，可得加熱位置從左壁面至下壁面中心 〈L〉t分別為?0.049 9、?0.052 6、?0.054 0，方差Lrms分別為0.002 4、0.001 8、0.001 5，由此可知局部加熱系統中加熱位置越靠近下壁面中心，其L(t)絕對值越大、振幅越小，系統主體LSC穩定性越高，LSC反轉可能性越低。

圖4 不同加熱位置及經典RBC的L(t)變化情況Fig. 4 Time series of L(t) of local heating cases and traditional RBC case

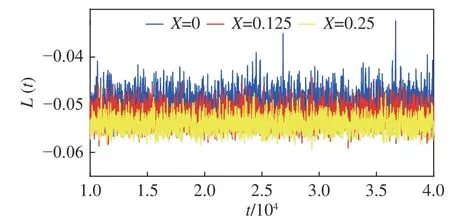
圖5 不同加熱位置的L(t)變化情況Fig. 5 Time series of L(t) of local heating cases

Sugiyama等[38]曾描述了角渦在LSC反轉過程中的作用，即由于角落邊界層分離羽流的能量補給，小的角渦會逐漸增大，直至達到腔體高度的一半，然后破壞主體LSC結構，并在相反方向上建立另一個新的LSC。由此我們知道反轉現象的產生與角渦的生長密不可分，為了觀察角渦及中心大渦的變化情況，繪制了流場云圖及動畫（在網刊資源附件中提供）。從動畫及圖6中可看出無論是否局部加熱，其基本流場結構均主要由中心大渦及角渦組成。其中局部加熱系統中下壁面角渦不穩定，且大小受限。雖然RBC系統中的角渦關于方腔中心的對稱性更強，θ、u、v的數值分布均具有更高的對稱性，但其中心大渦也被更劇烈地擠壓，更容易誘導渦的破碎和反轉。而在局部加熱系統演化過程中，系統熱羽流只能沿某一（距離加熱區域更近的）側壁上升，遇到下降的冷羽流時發生分離，在上壁面附近形成與RBC系統中相似的正常形態角渦，而在另一側由于缺少上升的熱羽流，只能在下壁面附近產生僅由冷羽流誘導的角渦。此時系統中下壁面角渦由于缺乏能量補給條件，顯然無法正常生長，使得系統LSC無法發生反轉。我們猜測，本文研究的局部加熱系統里由于下壁面的角渦缺乏持續的冷熱羽流相互競爭機制，導致該角渦大小無法突破LSC反轉的閾值，即達到腔體高度的一半，從而無法發生LSC反轉，這與Sugiyama等[38]描述的機制一致。此外，局部加熱系統中角渦的大小雖然受限制，但仍然會隨著時間演化不斷波動。

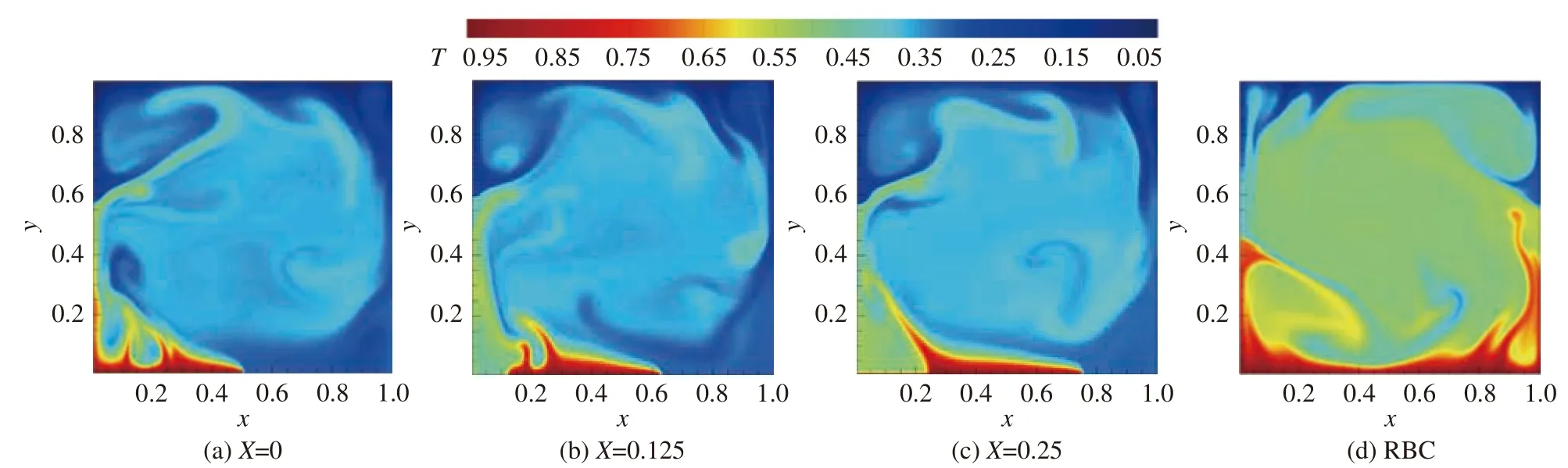
圖6 不同加熱位置及經典RBC瞬時溫度云圖Fig. 6 Temperature contours of local heating cases and traditional RBC case

2.2 不同位置的局部加熱條件對傳熱效率的影響

由于左右壁面均為絕熱條件，故只考慮豎直方向傳熱情況，通過Nu數對其進行量化，本文定義有效Nu數為：

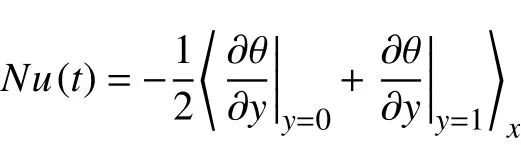
其中下邊界絕熱壁面 ?θ/?y=0，由于進出熱流的平衡，滿足下邊界加熱區域平均熱流密度為上邊界的兩倍，故根據上述公式仍能得到可靠的系統平均Nu數。圖7給出了系統達到統計穩態后，不同加熱位置及經典RBC系統的Nu(t)隨時間演化情況。為了更直觀地展示和對比，我們將RBC系統的Nu(t)上移4，而將X=0.125和X=0.25的Nu(t)下移了8和16。

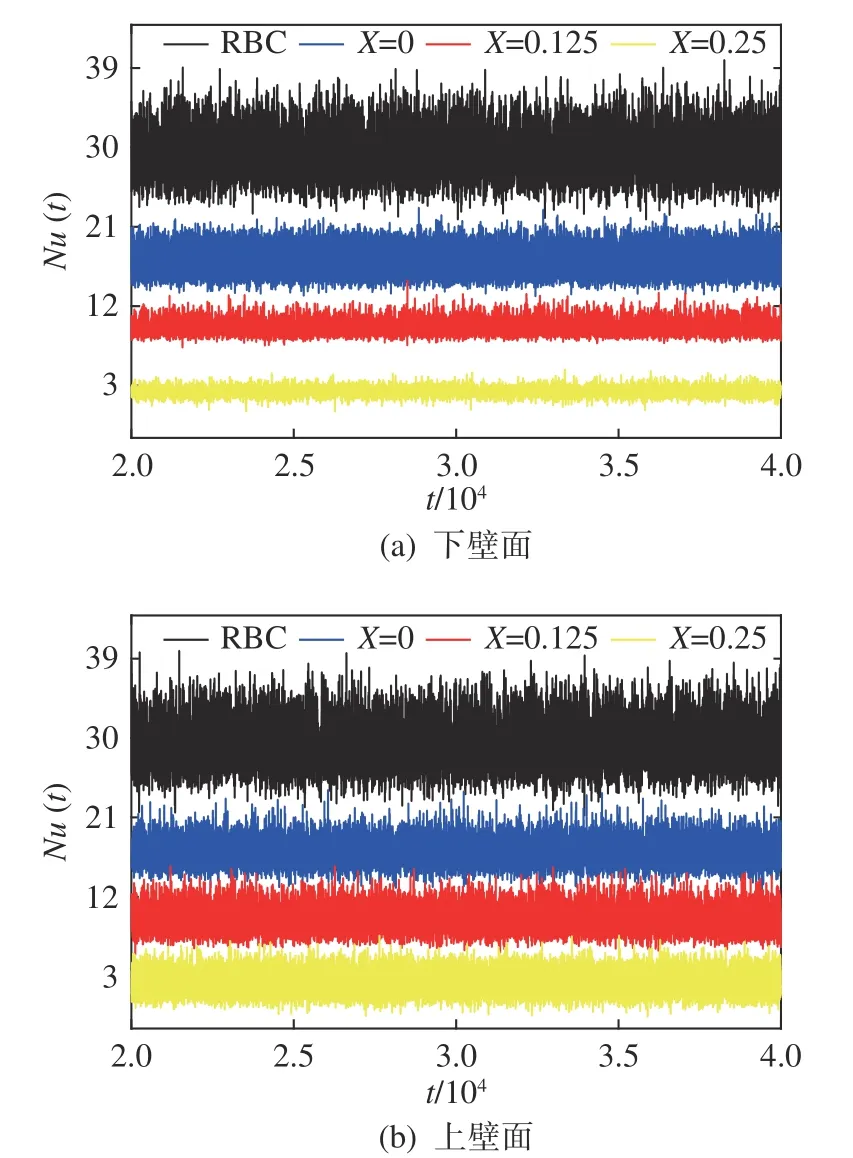
圖7 不同加熱位置及經典RBC的上下壁面Nu(t)變化情況Fig. 7 Time series of Nu(t) at the bottom wall (a) and top wall (b)from different cases

其 中RBC系 統 〈Nu〉t=24.92，如 上 文 所 提，與Zhang等[25]文獻給出的24.90基本一致。從圖中可以明顯看出的是，RBC系統的 〈Nu〉t比局部加熱系統振蕩更為劇烈，而局部加熱系統內部則是隨著加熱位置越靠近中心而越小。為了得到定量的數據，我們計算X=0、X=0.125、X=0.25三個局部加熱系統在統計穩態的 〈Nu〉t，結果分別為16.97、17.46、18.23。可以發現，雖然局部加熱系統 〈Nu〉t明顯小于RBC系統，但隨著加熱位置越靠近下壁面中心， 〈Nu〉t的值也會隨之越來越大，傳熱效率依次升高，這與前文總動能 〈Ek〉t、角動量絕對值 |〈L〉t|的相對大小保持一致。其中雖然局部加熱系統的加熱長度l=0.5，僅為RBC系統的一半，但其 〈Nu〉t可以達到傳統RBC的68.1% ～ 73.2%，遠高于設想的50%。而且通過比較分析，我們發現X=0.25系 統 〈Nu〉t比X=0.125系 統 增 長 了4.4%，比X=0系統增長了7.4%。也就是說，在局部加熱區域長度確定的情況下，除了Bakhuis等[33]通過將導熱及絕熱區域分布為數量盡量多的條紋圖案以提升系統傳熱效率外，我們也可以通過控制整體加熱位置，來使系統傳熱效率最大化。

觀察圖7（b）并與圖7（a）作對比，可以看出在達到統計穩態后，RBC系統上下壁面Nu(t)特征相似；在局部加熱系統中，雖然上壁面Nu(t)振幅區別不大，但加熱位置越靠近下壁面中心，下壁面Nu(t)幅值越小導致上下壁面之間差距越明顯。這是因為上壁面附近以側壁分離出的冷熱羽流共同作用為主，對其影響相近。而另一側由于沒有熱羽流的阻礙，冷羽流下降后會先到達下壁面而后橫向運動，再與相遇的熱羽流一同上升。結合云圖及動畫可知，加熱位置越靠近中心，即加熱區域離冷羽流到達下邊界位置越近，受其沖擊作用和橫向運動影響的范圍就越大，從而導致自由生長的熱羽流數量越少，因此加熱區域溫度脈動就越小，Nu(t)振幅也越小。

圖8展示了統計穩態時，下壁面加熱區域的時均溫度梯度分布，其證明加熱位置越靠近冷羽流沖擊點，其受冷羽流影響端溫度梯度就越大，即冷羽流作用程度越強。而中心加熱系統中，加熱位置最靠近冷羽流發生變向運動區域，其受影響最大，熱羽流生成數量始終維持在1～2個，因此熱羽流可以以近似一簇的狀態快速從左側壁上升進而與冷羽流進行相互作用，又因為其對于方腔中心而言具有更穩定的LSC結構，因此具有更高效率的對流換熱，故整體傳熱效率更高。

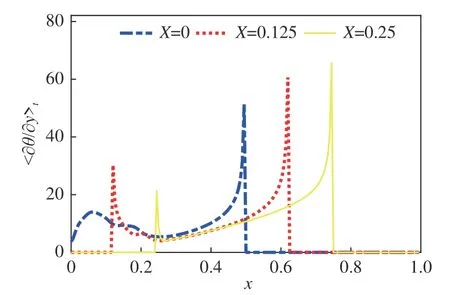
圖8 不同加熱位置系統的下壁面時均溫度梯度Fig. 8 Temperature gradient of the bottom wall of different heating position cases

3 結 論

本文以二維方腔RBC系統為基礎，通過直接數值模擬計算了Pr=2、Ra=1×108條件下，加熱區域長度l=0.5，加熱位置分別為X= 0、0.125、 0.25的三種局部加熱系統。分別研究了不同位置的局部加熱條件對系統總動能、角動量、LSC反轉及傳熱效率的影響。對結果進行分析，得出以下結論：

1）局部加熱系統中，加熱位置越靠近下壁面中心，其總動能和角動量絕對值越大、振幅越小，系統主體LSC穩定性越高；

2）局部加熱條件會對系統下壁面角渦的生長產生限制，進而抑制LSC反轉；

3）雖然加熱長度為RBC系統的一半，但局部加熱系統總動能〈Ek〉t可達到后者的62.5%～72.5%，傳熱效率可達到68.1%～73.2%；

4）在一定的加熱長度下，可以通過調整加熱位置令傳熱效率最大化，其中X=0.25系 統就比X=0系統增長了7.4%；

5）在沒有熱羽流上升側，冷羽流下降后到達壁面處改為橫向運動，該位置與加熱區域越近則對熱羽流數量和對應溫度脈動影響越明顯，其對應端點溫度梯度也越大。

由于本文計算選取局部加熱位置數量有限，因此想要得到更為確切的定量關系，還需大量不同加熱位置及加熱長度的計算結果。本文初步證明了加熱長度確定的情況下，可以通過加熱位置來控制傳熱效率。關于局部加熱條件對LSC反轉的影響，后續還會深入研究。除此之外，本文作為對非對稱局部加熱問題的初步研究，目前僅開展了二維直接數值模擬研究，后續我們將進一步開展三維問題的直接數值模擬與分析，以及相應的實驗研究。