熱湍流多重態與熱輸運效率實驗研究

謝毅超，陶 鑫，任 磊，夏克青

(1. 西安交通大學 航天航空學院， 機械結構強度與振動國家重點實驗室，西安 710049；2. 南方科技大學 力學與航空航天工程系，復雜流動及軟物質研究中心，深圳 518055)

0 引 言

湍流多重態是近期湍流研究的熱點問題[1]。湍流多重態通常是指在相同控制參數下，湍流系統會出現不同的流動結構和統計特性，比如在von Kármán旋轉湍流[2-5]、Taylor-Couette流動[6-9]、展向旋轉平板Couette流動[10-11]、球形Couette流動[12]和Taylor-Green湍流[13]中，人們均發現湍流系統會出現以不同的大尺度湍流結構為典型特征的多態現象。上述系統中觀察到的多態現象可以分為以下兩類：一類多態現象源于系統驅動力對稱性的改變或者驅動力在控制參數空間路徑的改變，例如Von Kármán旋轉湍流、Taylor-Couette流動和Taylor-Green湍流；另一類多態現象源于不同的初始條件，例如展向旋轉平板Couette流動。作為湍流的重要模型之一，浮力驅動的熱湍流（熱對流）是否也存在類似的多態現象備受關注。

熱對流現象廣泛存在于自然界和工程應用中，如海洋[14]和大氣[15]中的熱對流及核聚變反應堆包層[16]中的熱對流等。Rayleigh-Bénard（RB） 熱湍流是從眾多自然現象中抽象出來研究浮力驅動湍流的經典模型[17-19]。在RB系統中，通過加熱封閉對流腔體的下邊界，同時冷卻其上邊界，使流體在浮力的作用下產生對流。當上下邊界的溫差足夠大時，RB系統會進入湍流狀態，此時系統的溫度梯度主要集中于上下邊界處很薄的溫度邊界層內。溫度邊界層由于不穩定性生成冷（熱）羽流，羽流通過自組織，形成大尺度湍流結構[20]。

在Oberbeck-Boussinesq（OB）近似下，RB系統的控制方程為：

不可壓縮連續性方程

加入浮力項的Navier-Stokes（N-S）方程

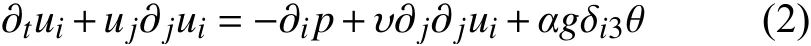
熱輸運方程

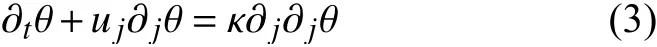
其中，ui(i= 1,2,3)為速度場，θ為溫度場，p為廣義壓強場；υ為運動黏性系數，α為熱膨脹系數，κ為熱擴散系數，δij為Kronecker符號。在OB近似下，方程（1～3）無量綱化后可以得到RB系統的兩個無量綱控制參數，即Rayleigh數（Ra）和Prandtl數（Pr），定義如下：

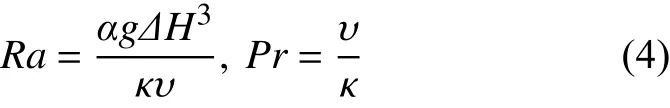
式中，Δ為上下邊界溫差，H為對流腔體高度。Ra數是無量綱化的溫差，用來衡量驅動浮力的大小；Pr數表征流體的物性參數。從實驗的角度，還需要引入系統的寬高比Γ=D/H來表征給定幾何形狀下對流腔體的空間約束程度，這里D為對流腔體的水平特征尺度。

RB系統的響應參數為Nusselt數（Nu）和Reynolds數（Re）。它們的定義分別如下：

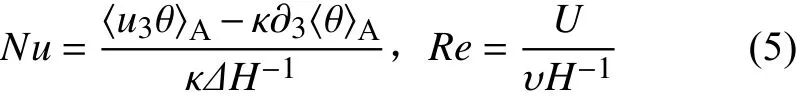
其中，＜···＞A表示對任意一水平面的面平均，u3為豎直方向的速度，U為系統的特征速度。Nu數表示RB系統傳熱效率與流體處于靜止狀態時熱傳導傳熱效率的比值，用于衡量系統的熱輸運效率。Re數衡量系統的動量輸運效率。

已有研究發現在圓柱對流腔體內的熱湍流會出現單環結構和雙環結構的大尺度湍流結構[21-22]。近期謝毅超等發現隨著Ra數在6.0×107～1.3×109范圍內的增加，圓環對流腔體中的RB熱湍流會從高傳熱效率的四極子湍流態演化到低傳熱效率的偶極子湍流態，這種流態轉變對應著系統的自發對稱破缺[23]。在轉變區間，系統呈現出多重態現象，即系統會在四極子態和偶極子態兩個亞穩態之間自主隨機的轉變。如果Ra繼續增加，系統會出現什么樣的流態，其又遵循什么樣的輸運規律是本文將要研究的問題。

需要指出的是四極子流態和偶極子流態與單環結構（雙環結構）湍流態[21-22]有著明顯的區別。單雙環結構的轉變存在于實驗所包括的所有Ra數工況下，并且這兩個狀態的持續時間均和大尺度湍流結構的特征時間相當；而偶極子流態和四極子流態的轉變只發生在有限的Ra數范圍內，且系統處在各態的時間遠大于大尺度湍流結構的特征時間；其次，單雙環結構流態轉變并未導致系統的Nu數等響應參數出現明顯的雙峰結構。

1 實驗裝置和測量方法

實驗采用了圓環對流腔體。為了表征圓環體的空間約束效應，除了寬高比Γ以外，還需要引入內外徑比γ=Di/Do，這里Di是圓環體內圓柱的外徑，Do是圓環體外圓柱的內徑。實驗中采用了兩套幾何參數接近、但特征高度不同的對流腔體，它們的高度分別為H= 150 mm（大對流腔體）和H= 104 mm（小對流腔體）。大對流腔體和小對流腔體的寬高比和內外徑比分別為Γ= 2、γ= 0.9和Γ= 1.88、γ= 0.9。

實驗裝置卡通圖見圖1，每個對流腔體由三部分組成，分別是無氧紫銅（TU1）制作的冷卻上板、加熱下板和有機玻璃制作的邊壁。上下板和流體接觸的表面鍍了鎳薄層保護紫銅。上板內部刻有圓環形的流道，深20 mm，寬度5 mm，來自恒溫水浴（Julabo DD1000）的冷卻水流經流道，冷卻上板。下板內埋有兩層鎳鉻電阻絲（Omega，NI80-012-200），由99.99%電壓穩定性的直流電源（Armetex，XG300-5）提供恒定的加熱。為了實現高精度的熱輸運測量，實驗使用了邊壁保溫罩和底部保溫罩等輔助保溫裝置。整個對流腔體放置于保溫裝置內，并將保溫裝置和對流腔體之間的空隙填滿保溫棉。

實驗采用熱敏電阻（Omega Inc，44031）實現高精度的溫度測量：分別在上下板中沿角向均勻布置8個溫度探頭，測量其溫度。結合同步測量的加熱板輸入電壓U和電流I，可以計算系統的Nu數，Nu=UIH/[χΔπ(D2o?D2i)/4] ，其中χ為流體的導熱系數。為了同步測量大尺度湍流結構與熱輸運效率，在對流腔體外邊壁，距離下板高度為z = H/2的位置沿角向均勻布置16個溫度探頭，并在z= 3H/4 的位置沿角向均勻布置8個溫度探頭。實驗開始前，對用到的47個溫度探頭進行標定，其相對溫度測量的精度好于0.01 K。通過數據采集器（Keithley 2701）實現熱敏電阻阻值、輸入電壓和電流的測量，采樣頻率為0.21 Hz。實驗測量發現z=H/2 處和z= 3H/4 處的溫度信號呈現的信息是一致的，因此在下文中主要分析z=H/2處的溫度測量。

實驗使用去離子水作為工作物質。大對流腔體上下板的溫差范圍為2.4 K ≤Δ≤ 34.3 K , 對應的Ra數范圍為 2.0×108≤Ra≤ 2.9×109。流體的平均溫度設定為30℃，對應的Prandtl數為Pr= 5.4。通過PID調制，使得上板的溫度為恒定值，其近似地滿足恒溫邊界條件；下板為恒熱流邊界條件；邊壁為絕熱邊界條件。對于每一個Ra工況，先通過PID溫控程序調制下板輸入功率和上板溫度，使系統收斂到預設的Ra值，隨后固定加熱板的輸入功率并且等待系統穩定2.5 h以后，開始采集數據。根據Ra數的不同，實驗測量的時間不同，當處于最大的Ra數時，測量時間最短，為12 h；在后文提到的轉變區間內的工況，測量時間最長，為72 h。

實驗中，使用粒子圖像測速儀（particle image velocimetry, PIV，Lavision）直接測量了小對流腔體內的大尺度湍流結構。為了實現PIV測量，將上板用透明的藍寶石代替，激光光片從水平方向射入對流腔體，將攝像機置于對流腔體正上方，從而獲得對流腔體不同高度的水平二維速度矢量場。實驗中分別測量了四極子流態和偶極子流態的空間結構；對于每一個流態，測量了5個不同高度；每個高度的測量時長為20 min，其采樣頻率為15 Hz。

2 結果分析

2.1 大尺度湍流結構直接測量

通過測量對流腔體z=H/2 處的溫度空間分布，文獻[23]在小對流腔體中發現熱湍流會出現偶極子流態和四極子流態。在本文中，利用PIV直接測量了小對流腔體中這兩種流態的空間結構。

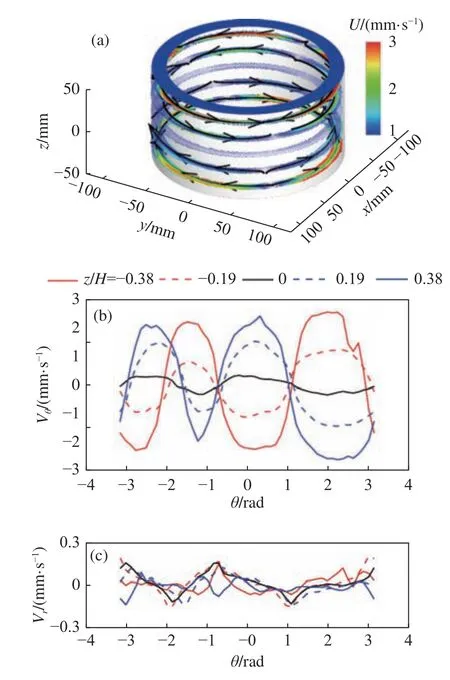
圖2（a）展示了偶極子流態時對流腔體五個高度的時均速度矢量場和部分流線。從流線方向可以看出封閉對流腔體內存在兩個大尺度渦結構，其路徑分別為（abcdefa）和（agcdhfa）。圖2（b）和圖2（c）分別展示了時間和徑向平均后的角向速度與徑向速度分布。與文獻[23]溫度測量中觀察到的偶極子流態類似，角向速度分布呈現偶極子結構，同時徑向速度比角向速度小一個數量級，因此圓環腔體內的偶極子流態近似地看作沿著角向和軸向的準二維流動。

圖3（a）展示了四極子流態時對流腔體五個高度時均速度矢量場和部分流線。圖3（b）和圖3（c）分別展示了時間和徑向平均后的角向速度與徑向速度分布。結合圖3（a、b） 可以看出圓環對流腔體中存在4個大小不等且上下貫穿的大尺度渦結構，這與文獻[23]中溫度測量得到的四極子流態一致。比較圖3（b）和圖3（c）可以看出四極子流態的徑向速度比角向速度小一個數量級，因此圓環對流腔體中的四極子流態也可以看作沿角向和軸向的準二維流動。由于溫度場和速度場反映的大尺度結構是一致的，因此可以通過長時間的溫度測量來研究大尺度湍流渦結構的動力學特性。

2.2 熱湍流多重態

這部分主要討論RB熱湍流中的多重態現象。由2.1節中的結論可知，在RB湍流中速度場和溫度場呈現的信息一致，因此可以通過直接測量溫度場，得到對流腔體中的大尺度湍流結構信息。小對流腔體的結果已經在參考文獻[23]中予以報道，本文將主要關注大對流腔體中的多重態現象。實驗中采用多溫度探頭技術[24-25]測量大尺度流動結構動力學特性。在每一時刻，將對流腔體邊壁z=H/2處的溫度空間分布進行離散傅里葉展開：

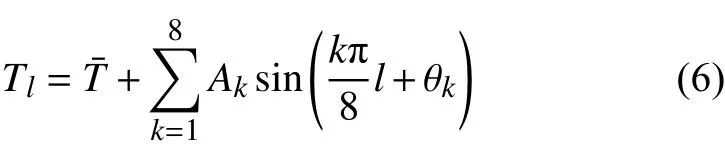
其中，為16個溫度探頭的平均溫度，Ak為第k階模態的幅值，θk為第k階模態的初相角，l為從0到15的整數。在本文研究的γ≈ 0.9的圓環體中，流動為沿角向和軸向的準二維流動，因此通過測量角向溫度分布可以更加清晰地反映大尺度湍流結構。

圖4（a～d）分別展示一階至四階傅里葉模態主導時z = H/2處的溫度分布和對應階的三角函數擬合曲線。與文獻[23]中的結果一致，大尺度湍流結構會出現一階模態和二階模態主導的湍流態 （圖4（a、b））；不同的是，在大對流腔體中還觀測到了三階傅里葉模態（圖4（c）） 和四階傅里葉模態（圖4（d）） 占主導的情況。傅里葉模態與流態的對應關系為：一階模態對應偶極子流態，二階模態對應四極子流態，三階和四階模態對應高階流態。

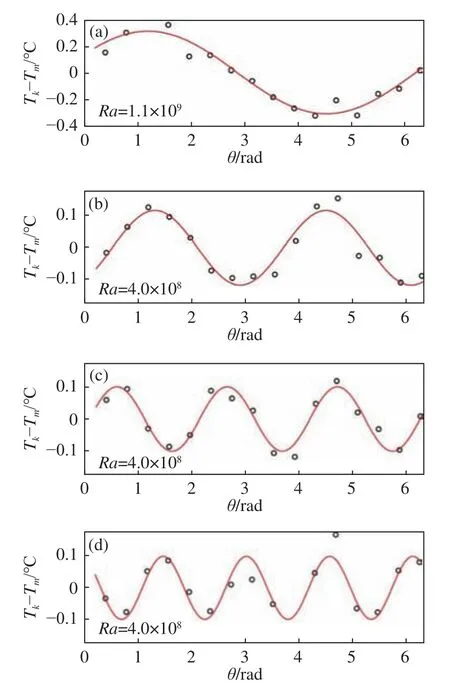
圖4 對流腔體z = H/2處不同模態主導時對應的溫度分布：（a）一階，（b） 二階，（c） 三階， （d） 四階Fig. 4 Fourier modes of the azimuthal temperature profile measured at half-height of the convection cell: (a) the first mode,(b) the second mode, (c) the third mode and (d) the fourth mode

為研究流態隨Ra數的變化規律，引入模態相對強度Sk[26]，其定義為：

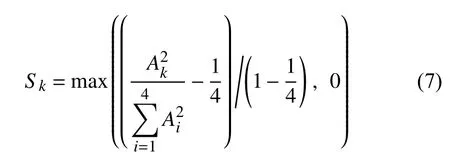
這里k為1到4的整數。當第k階模態的能量Ek=A2k占總能量的一半以上時，認為其是主導流態，此時對應的Sk大于1/3；如果第k階流態的能量小于所有流態能量的平均值，對應的Sk為0。由于長時間測量過程中有一個溫度探頭出現故障，為了統一所有Ra數的數據處理方法，我們在z=H/2選擇了8個角向均勻分布的溫度探頭進行流態分析。研究發現16個溫度探頭和8個溫度探頭獲得的前四階流態信息是一致的。

圖5（a） 展示了Ra= 4×108時模態相對強度Sk的時間序列。為了更加清晰的看到大尺度湍流結構的動力學特性，圖中的時間序列經過了一個低通濾波，后文將使用相同的方法處理數據。從中可以清晰地看到一階模態到四階模態陣發主導的現象。圖5（b）展示了Ra= 1.13×109時的模態相對強度的時間序列，可以看出此時系統先從偶極子流態主導的狀態轉變到了四極子流態主導的狀態，四極子流態持續了接近30個小時，偶極子流態又重新成為了主導流態。這個流態轉變過程與文獻[23]中報道的類似，說明大對流腔體中也存在以不同大尺度湍流結構為典型特征的多重態現象。進一步分析給出大對流腔體流態的 轉 變 區 間 為1.0×109≤Ra≤ 1.4×109（見 圖11和圖12）。

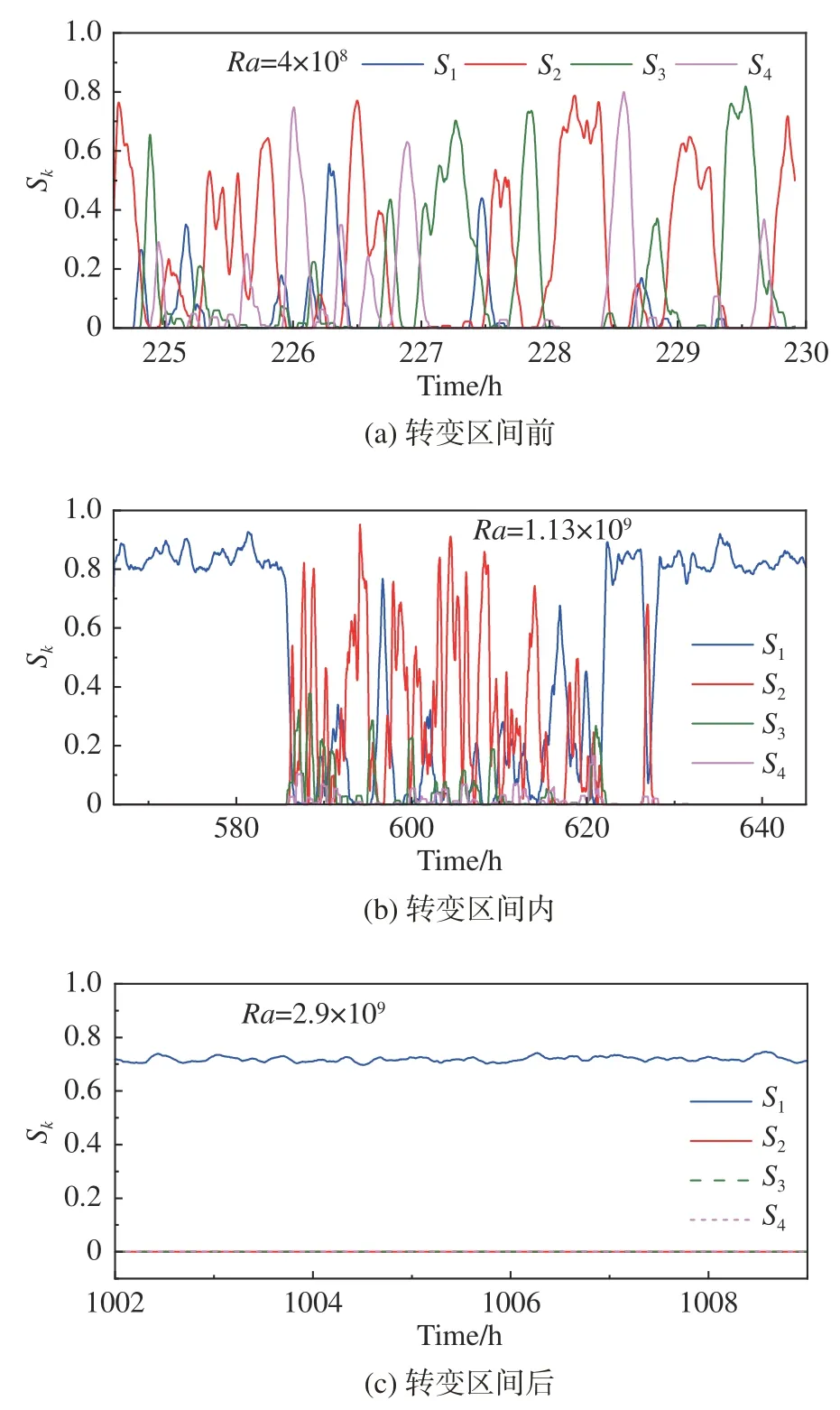
圖5 轉變區間前 、轉變區間內 、轉變區間后前四階傅里葉模態相對強度Sk的時間序列Fig. 5 Time series of Sk ( k = 1,2,3,4 ) : (a) before, (b) during and(c) after the transition

圖5（c） 展示的是Ra= 2.9×109的相對模態強度。由于此時大尺度結構完全由偶極子流態主導，其它階流態的相對強度始終為0。綜合圖5（a～c），發現隨著Ra數的增加，大尺度湍流結構從高階模態主導的流態轉變到了最低階的一階模態，這與文獻[23]中的發現是一致的；與文獻[23]不同的是在大對流腔體中Ra比較小的時候，大尺度湍流結構呈現出一階到四階模態交替隨機出現的狀態（圖5（a））。而在文獻[23]中，轉變之前的大尺度湍流結構只存在偶極子流態。

從圖5的分析中可以清楚地看出在大對流腔體中也存在多重態現象，那么不同流態出現的機率隨Ra是如何變化的呢？圖6反映的是不同流態主導時間占總時間的比重隨Ra數的變化。在轉變區間之前，偶極子流態主導時間比小于8%，而四極子流態主導時間比重相對快速上升，此外高階模態占據了大約50%的時間，且高階模態比重隨Ra增大而減少。進入轉變區間時，高階模態相對一階和二階模態的占比已可以忽略。轉變區間內，偶極子流態主導時間占比開始驟升，而四極子流態占比驟降。轉變區間過后，全時域由偶極子流態主導。因此，圖6反映了大尺度湍流結構隨著Ra數的增加是如何從高階流態動態地演化到了最低階的湍流態。

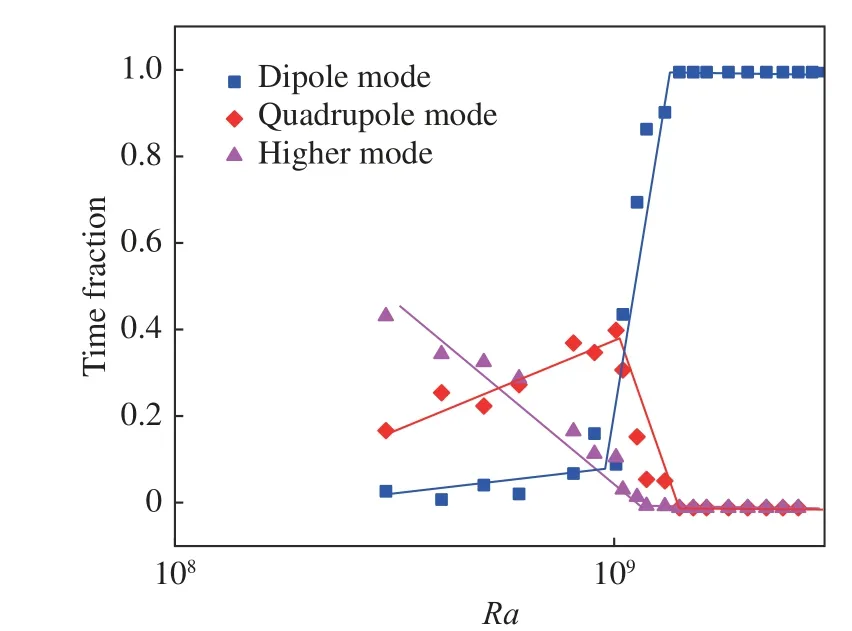
圖6 不同模態時間占比隨Ra數的變化Fig. 6 Time fractions of different flow modes versus Ra

2.3 流態與熱輸運效率的對應關系

圖7（a）為流態轉變區間內S1、S2的時間序列，圖7（b）為對應Nu數的時間序列，可以看出偶極子流態主導時，RB系統的時均Nu數為Nu= 64 ± 0.12；而四極子流態主導時，系統的時均Nu數為Nu= 66 ± 0.21。由此可見，流態與輸運效率存在明確的一一對應關系，且四極子流態的熱輸運效率高于偶極子流態。

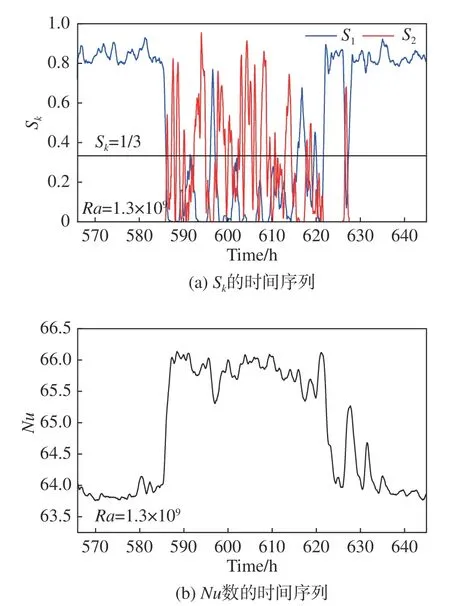
圖7 轉變區間Sk與對應的Nu數的時間序列Fig. 7 Time series of S1, S2 and the corresponding Nu during the transition

圖8給出了Ra= 1.06×109長時間采樣的S1、S2和Nu數的時間序列。可以看出偶極子流態和四極子流態隨機交替成為系統的主導大尺度湍流結構，與此對應的是系統的Nu數也在兩個狀態之間變化。這與圖7給出的例子是一致的。此外，在整個流態轉變區間內（1.0×109≤Ra≤ 1.4×109）都觀察到了類似于圖8中所展示的現象，說明熱湍流多態現象以及流態和輸運效率一一對應是轉變區間的普遍現象。

圖8 Ra = 1.06×109時S1、S2與 對應的Nu數的長時間序列Fig. 8 Long time series of S1, S2, and the corresponding Nu at Ra = 1.06×109

為了從統計上分析流態與輸運效率的關系，分析Sk和Nu數的互相關函數。兩個變量x和y的歸一化互相關函數定義為：

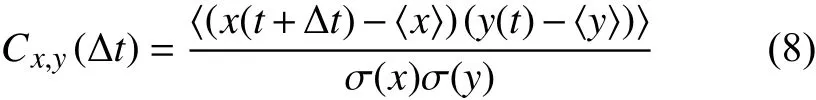
其中＜···＞表示時間平均。互相關函數表征的是兩個時間序列在Δt間隔下的相關程度，其峰值代表兩個時間序列相關程度達到極值的情況。峰值對應的時間延遲Δt如果是正值，表示x、y兩組序列中的相關信號，在y序列中發生要先于在x序列；反之同理。

圖9（a）和圖9（b）分別展示了Ra= 1.13×109時，偶極子流態相對強度S1和Nu數以及四極子流態相對強度S2和Nu數的互相關函數。可以看出S1和Nu呈負相關，而S2和Nu呈正相關，說明偶極子流態越強，系統的熱輸運效率越低；四極子流態越強，系統的熱輸運效率越高；同時兩個互相關函數的峰值均對應于負的時間延遲，說明大尺度湍流結構的變化引起了系統熱輸運效率的變化。

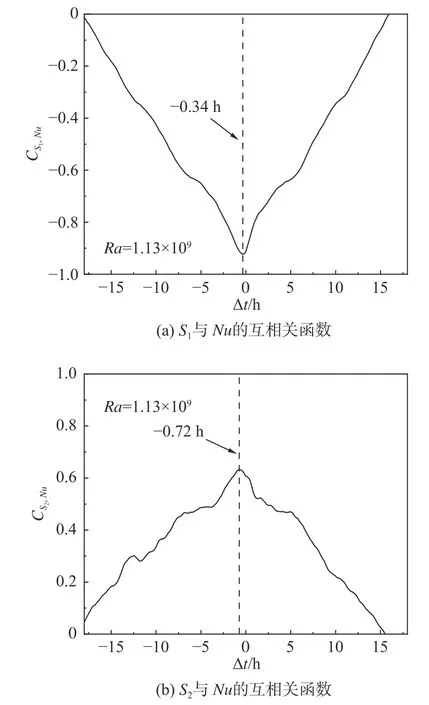
圖9 S1與Nu、S2與Nu的互相關函數Fig. 9 The cross-correlation function between(a) S1 and Nu and (b) S2 and Nu

從圖6中可以看出Ra= 4.0×108時，大尺度湍流結構主要由四極子流態和高階模態占主導的流態主導。將它們的相對強度S2、Sh分別和Nu做互相關分析，這里Sh=S3+S4是高階模態占主導的流態的相對強度。圖10（a）和圖10（b）分別展示了S2和Nu數以及Sh和Nu數的互相關函數。可以看出，四極子流態與熱輸運效率呈現負相關，同時高階模態占主導的流態與熱輸運效率呈現正相關，再次說明高階模態越強，熱湍流系統的熱輸運效率越高。與圖9不同的是，圖10中互相關函數峰值的時間偏移并不明顯，且其相關系數較小，這主要是由于Ra較小時，各階模態主導時間尺度較短，且Nu數有較強的漲落。

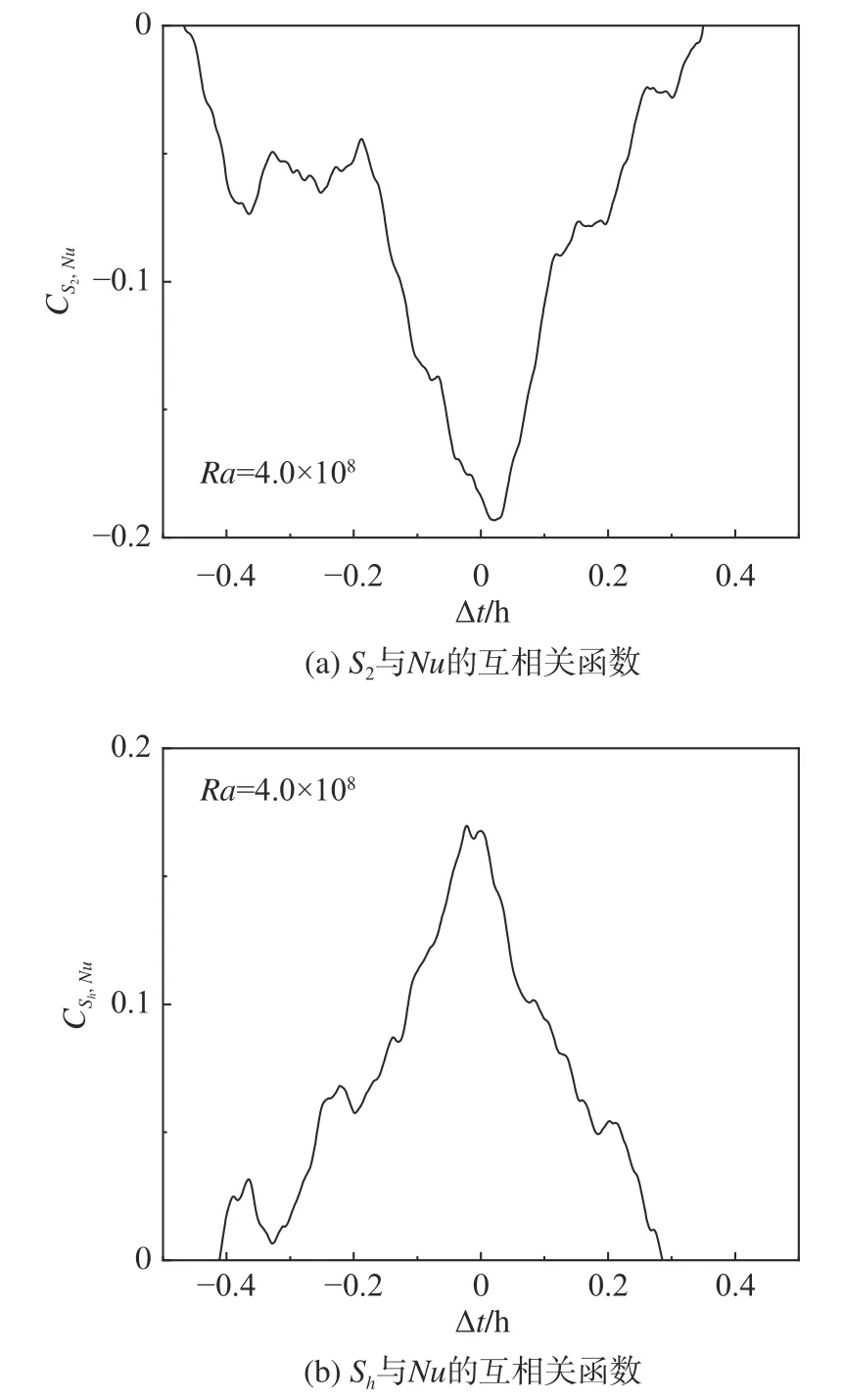
圖10 S2與Nu、Sh與Nu 的互相關函數Fig. 10 The cross-correlation function between(a) S2 and Nu and (b) Sh and Nu

結合圖9和圖10可以得出：高階模態主導湍流態的輸運效率高于低階模態主導湍流態，即高對稱性流態熱輸運效率高于低對稱性流態，這為通過主動調控湍流態從而調控系統的熱輸運效率提供了基礎。目前，我們正在開展這方面的工作。

2.4 傳熱標度率

圖11（a）展示的是Nu數隨Ra數的變化關系，橫坐標和縱坐標都為對數坐標；圖11（b）是使用補償畫法繪制的半對數圖，縱軸是Nu·Ra?0.274，橫軸是Ra的對數坐標，其中黑色方塊和紅色三角分別對應小對流腔體和大對流腔體中測得的Nu數。小對流腔體的數據已經發表于文獻[23]。

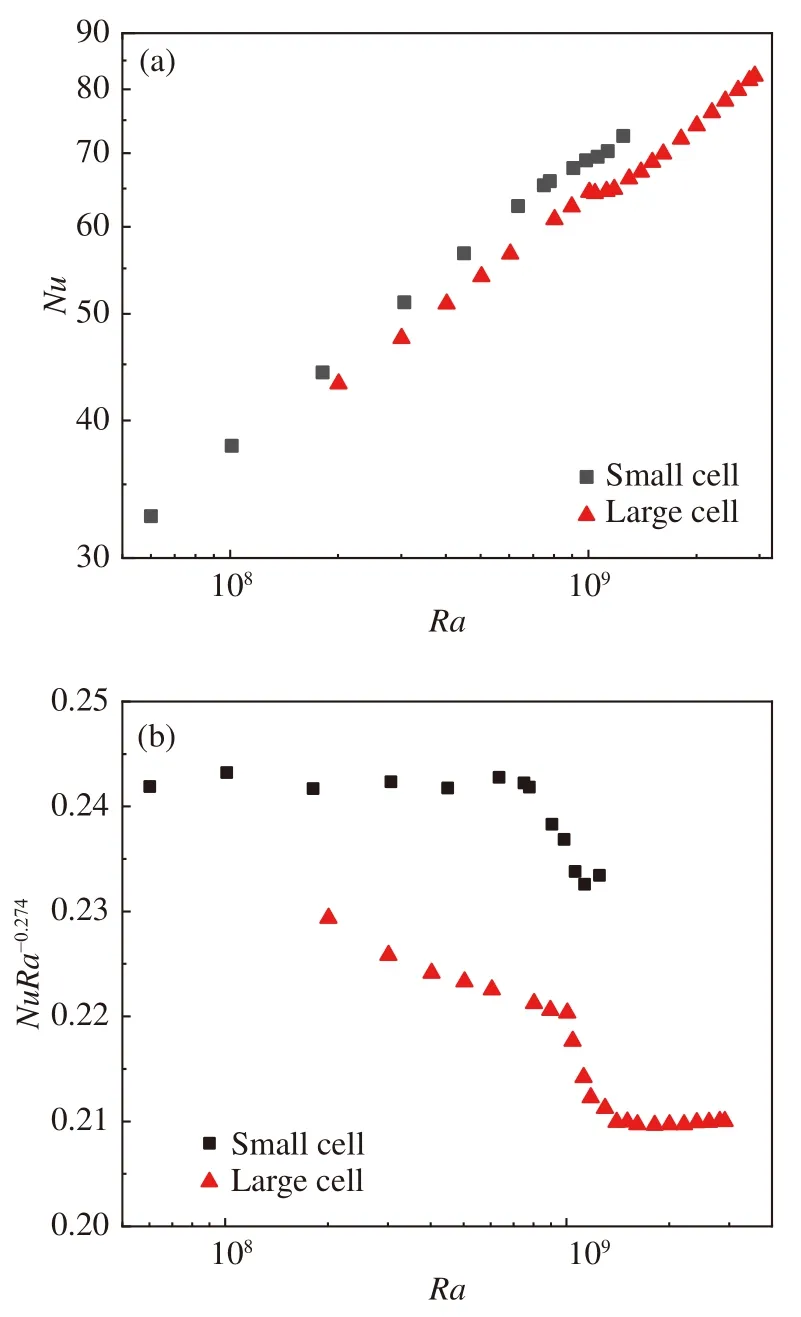
圖11 (a)時均Nu與Ra的函數關系；(b) 補償畫法下的時均Nu~Ra關系圖Fig. 11 (a) Time-averaged Nu as a function of Ra; (b) timeaveraged Nu compensated by Ra?0.274 as a function of Ra

從圖11（a）可以看出大對流腔體的傳熱效率整體低于小對流腔體，造成這一區別的主要原因可能是對流腔的尺寸越小，漏熱對其熱輸運效率的影響越大。對比圖11（b） 中的補償畫法圖可以看出，Nu數在兩個對流腔體中都發生了一個明顯的轉變，但是轉變的Ra數區間略有不同：在小對流腔體中，熱輸運轉變的區間為6.4×108≤Ra≤1.1×109，而在大對流腔體中是1.0×109≤Ra≤1.4×109。結合2.2節中流動模態分析發現，在大對流腔體中系統傳熱效率出現明顯轉變的區間內，湍流大尺度流動結構在四極子流態和偶極子流態之間發生頻繁的轉變（見圖8），此時熱湍流出現多重態，這與小對流腔體中觀察到的現象是一致的。

由于小對流腔體能夠承受的最大溫差的限制，其最大的Ra數約為1.2×109，此時系統剛剛進入由偶極子流態主導的區間。在大對流腔體中，通過增加腔體高度，在和小腔體相同的溫差下，可以實現更大的Ra數，從而可以在更加寬的Ra數范圍內研究RB熱湍流系統的輸運特性。從圖11（b）可以看出，在大腔體中，系統在進入偶極子流態主導的參數區間以后（Ra＞ 1.4×109），其熱輸運的標度率為Nu～Ra0.274，這個標度律指數與系統單純由四極子流態主導時是一致的（Nu～Ra0.274）。由于在大腔體中轉變區間前的流態既包括四極子流態又包括高階流態，且高階流態的時間比重隨著Ra數的增加而減小，因此轉變區間之前的標度律為Nu～Ra0.25，小于系統由單一流態主導時的標度律指數。

由于偶極子流態和四極子流態具有不同的熱輸運效率，因此湍流大尺度流動在這兩個流態之間轉變時，系統的Nu數會呈現出強烈的脈動。利用Nu數的標準差來衡量其脈動情況。圖12中展示的是σNu隨著Ra數的變化關系，其中小對流腔體的數據來源于文獻[23]。與小對流腔體中的數據一致，大對流腔體中的σNu也在流態轉變區間呈現出一個尖峰。值得注意的是盡管兩個對流腔體中Nu數的絕對值有差別，但是它們的標準差卻十分接近。由圖11和圖12可見當流動被偶極子流態主導以后，其σNu小于0.1且隨著Ra的增加幾乎不變，說明過了轉變區間以后的偶極子流態大尺度結構非常穩定。

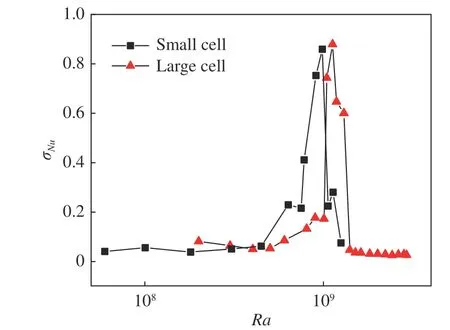
圖12 半對數坐標下Nu的標準差σNu與Ra的關系圖Fig. 12 The standard deviation of Nu as a function of Ra on a semilog plot

2.5 偶極子流態大尺度湍流結構的動力學特性

從圖6可以看出，隨著Ra數的增加，RB系統會進入流態轉變區間，此時偶極子流態和四極子流態交替成為主導流態，系統呈現出多重態。隨著Ra數的進一步增加，偶極子流態成為唯一主導的流態，因此這一節主要研究偶極子流態在轉變區間和轉變之后的動力學特性。

圖13（a） 展示的是轉變區間內（Ra= 1.13×109）偶極子流態強度和相位隨著時間演化的一個例子。圖中不同的顏色代表不同的時刻；徑向坐標軸代表偶極子流態的強度A1；角向坐標軸代表偶極子流態的相位θ1，其定義為大尺度流動結構上行處的角向位置。圖13（b）是轉變區間不同Ra數下偶極子流態強度和相位隨時間變化曲線，圖中的箭頭代表時間演化的方向。從圖13（a）可以看出，偶極子流態主導時具有一個偏好的相位角。當偶極子流態逐漸增強時，如果其相位不處于偏好位置，它將通過角向游走運動到偏好位置。圖13（b）是不同Ra數下的偶極子流態相位游走圖，與圖13（a）中的情況類似，當偶極子流態逐漸增強時，其相位會靠近并最終停留在偏好位置附近，這是偶極子流態在轉變區間時的普遍現象。

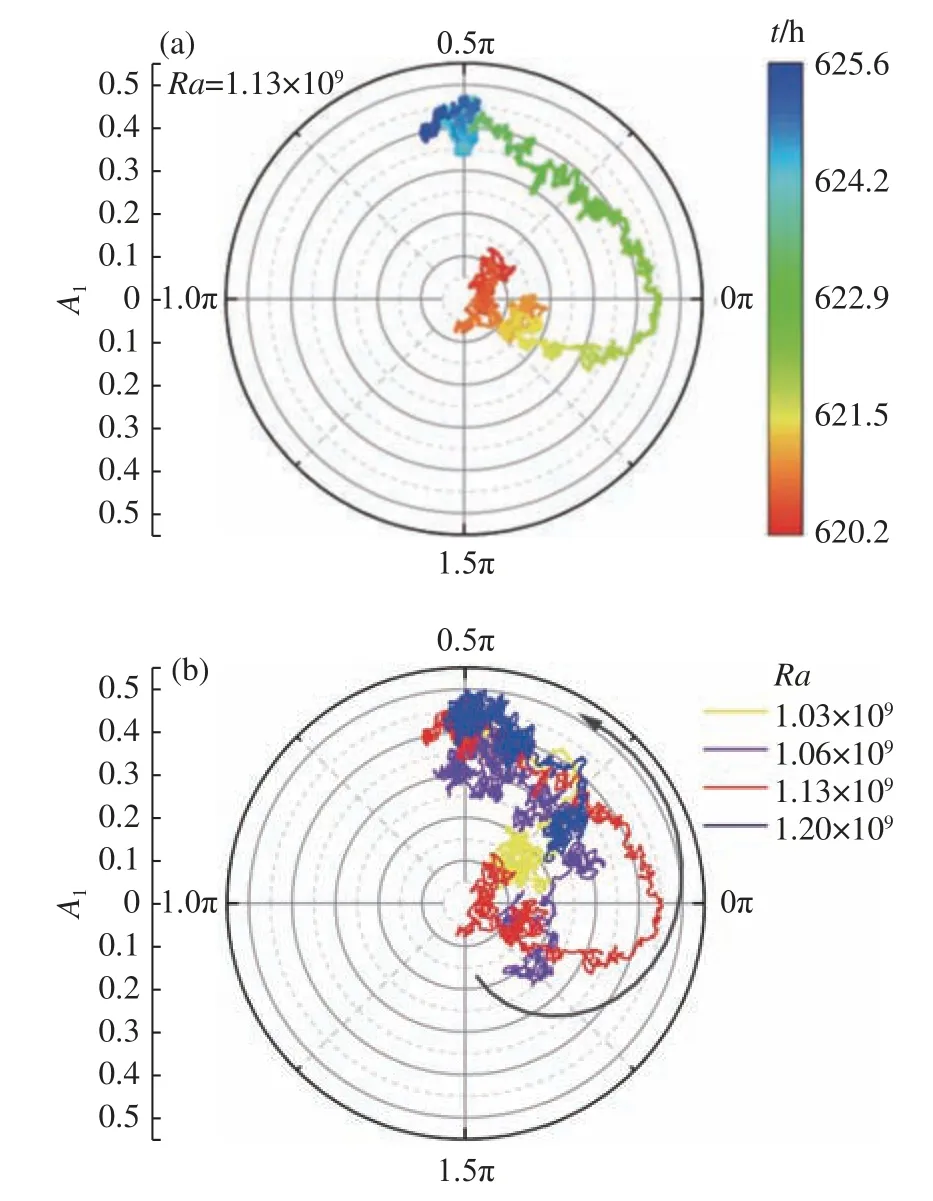
圖13 轉變區間偶極子流態強化過程：(a) 相位游走與時間的關系；(b) 不同Ra下的相位游走Fig. 13 The azimuthal meandering of the dipole mode (a) at Ra = 1.13 ×109 and (b) at various Ra

當系統經過轉變區間后（Ra＞1.4×109），大尺度湍流結構完全由偶極子流態占據。圖14（a） 是由偶極子流態完全主導時其強度和相位分布圖；圖14（b） 是偶極子流態強度A1的概率密度函數，黑色實線為標準高斯分布，插入圖是A1的標準差 σA1隨Ra數的變化關系；圖14（c） 是偶極子流態初相角θ1的概率密度函數，黑色實線為標準高斯分布，插入圖為θ1的標準差 σθ1隨Ra數的變化關系。

從圖14（a） 可以看出偶極子流態強度隨著Ra數增加而增加，且其相位的漲落范圍逐漸減小：Ra=1.6×109時θ1的漲落范圍為27°，而Ra= 2.9×109時θ1的漲落范圍為7°。此外，不同時刻的θ1都匯聚于系統偏好的相位角處，表明偶極子流態具有明確的相位偏好，并且該方向與轉變區間偶極子流態的偏好方向吻合。留意到在圓柱對流腔體中，大尺度湍流結構也存在相位偏好現象[21,25,27]，同時相位存在周期性振蕩[28]。而在大圓環對流腔體中由偶極子流態主導時，并沒有觀測到明顯的周期振蕩特性，說明強空間約束不但會改變大尺度湍流結構的空間結構，也會影響其動力學特性。

圖14 (a) 轉變區間后偶極子流態強度和相位分布； (b，c) 偶極子流態幅值A1與相位θ1的概率分布函數，嵌入圖為對應量的標準差隨Ra數的變化Fig. 14 (a) The phase θ1 and amplitude A1 of the dipole mode after transition; (b) the PDFs of A1 and its standard deviation σA1 as a function of Ra; (c) the PDFs of θ1 and its standard deviation σθ1 as a function of Ra

從圖14（b） 和圖14（c） 可以看出，不同Ra數時標準化以后的偶極子流態強度和相位大致重疊在一起，且可以用高斯函數來近似描述，說明偶極子流態在占主導以后其動力學特性不再依賴Ra。此外，偶極子流態強度A1的標準差 σA1隨Ra的增加而緩慢減小，其相位θ1的標準差 σθ1隨著Ra的增加而減小，表明偶極流態的角向運動隨著Ra的增加會被抑制，同時其強度的相對漲落 σA1/A1也在減小，說明偶極子流態隨著Ra的增加變得更加穩定。

2.6 空間約束與熱輸運

已有研究發現，通過在RB系統中引入空間約束可以實現熱輸運的強化，例如文獻[29]中發現將矩形對流腔體沿著一個水平方向壓縮，RB系統的熱輸運效率最高可以提升17%。在本文研究的圓環對流腔體中，內外徑比γ就是用來衡量系統空間約束強度的一個重要參數。圖15展示了寬高比Γ= 2，內外徑比γ分別為0.5和0.9的兩個圓環對流腔體的Nu數。圖中Γ= 2、γ= 0.5的數據來源于文獻[30]，其大尺度湍流結構一直處于四極子流態。

圖15 半對數坐標下時均Nu與Ra的補償畫法圖Fig. 15 Time-averaged Nu compensated by Ra?0.274 as a function of Ra on semilog scale

由圖15可以看出空間約束究竟是增強還是抑制湍流熱輸運與Ra數（即湍流態）相關。當Ra＜1×109的時候，強空間約束條件下（γ= 0.9），系統出現更高階的流態。由2.3節的討論可知更高階的流態對應更強的輸運效率，因此強空間約束可以增強系統的熱輸運效率。當Ra＞1×109的時候，強空間約束下（γ=0.9） 熱湍流的流動結構已經被偶極子流態占主導；而此時γ= 0.5的對流腔體中流動結構仍然是四極子流態，因此 在這種情況下γ= 0.5的對流腔體熱輸運效率更高。

3 結 論

本文以水為工作流體，通過實驗研究了Rayleigh-Bénard（RB）熱湍流中的多重態現象和熱輸運效率。通過系統地測量兩個寬高比和內外徑比接近，但是特征高度不同的圓環對流腔體中的大尺度湍流結構和熱輸運效率，得出以下結論：

1）利用PIV直接測量了偶極子流態和四極子流態的空間結構，明確了圓環對流腔體RB熱湍流中大尺度結構的速度分布和溫度分布高度一致。因此可以通過直接測量溫度空間分布得到大尺度流動的空間結構。此外，在內外徑比γ= 0.9時，圓環對流腔體中的大尺度流動結構可以近似地看作沿角向和軸向的準二維流動。

2）在文獻[23]的基礎上，再次確認了熱湍流存在多重態現象，即在相同的控制參數Ra數下，RB系統會出現不同的大尺度湍流結構和熱輸運效率。

3）通過同步測量大尺度湍流結構和熱輸運效率，發現了大尺度湍流結構與熱輸運效率存在一一對應關系，并且由高階模態主導的湍流態的熱輸運效率高于由低階模態主導的湍流態。為通過調控大尺度湍流結構從而調控熱湍流輸運效率提供理論基礎。

4）隨著Ra數的增加，偶極子流態強度的相對漲落和相位漲落降低，說明偶極子流態變得更加穩定。與圓柱對流腔體中大尺度湍流結構（大尺度環流）類似，偶極子流態也存在偏好的相位角，但是圓柱對流腔體中大尺度結構相位的周期性振蕩在圓環對流腔體中并不存在，說明空間約束不僅會改變大尺度湍流結構的空間結構，也會影響其動力學特性。

5）通過對比不同空間約束程度的圓環對流腔體的熱輸運效率，發現空間約束增強或抑制湍流熱輸運效率取決于其對對流腔體中的流動狀態的調控：當空間約束導致系統出現更高階流動模態主導的流態時，空間約束會增強熱輸運；反之，當空間約束導致系統出現更低階流動模態主導的流態時，空間約束則會抑制湍流熱輸運。