基于Delaunay三角網法的土石方量計算精度探討

候漢霜

(深圳市長勘勘察設計有限公司，廣東 深圳 518003)

1 引 言

土石方量的計算結果關系到工程項目的各方利益，目前我們常采用的土石方量計算方法有斷面法、方格網法、等高線法、平均高程法和DTM(數字地面模型)法等。其中，每一種計算方法都有其適用條件和適用范圍，斷面法計算土石方量適合在線狀地形使用，比如道路、河流渠道等；方格網法在比較平坦的地區或者地形起伏不大的場地上更經濟實用；而在地形起伏較大、精度要求高的區域則需使用DTM法來計算土石方量較為合理。DTM法由于考慮了地形特征(采用不規則三角網TIN法建模)，并以原始測量采集的數據作結點的三角形為最小計算單元，從理論上來說是計算土石方量最為精確的方法。而通過建立Delaunay三角網保證得到的是最優的TIN模型，一般情況下是計算土石方量的最佳選擇。目前，主流的Delaunay三角網生成算法有三種：分割合并法、逐點插入法和三角網生長法。本文采用三角網生長法編寫基于Delaunay三角網的土石方計算程序，探究Delaunay三角網法土石方計算的方案與南方CASS軟件中傳統三角網法方案對比在土方量計算精度的偏差。

2 基于Delaunay三角網法的土石方量計算方法

土石方量的計算是通過地形表面模型和設計表面模型進行疊加，求出疊加后所夾空間區域的體積從而得到土石方量。這里需要分別建立地形表面TIN模型和設計表面TIN模型。

2.1 地形表面TIN模型的構建

要建立地形表面TIN模型必須先確定TIN模型中三角形的形成法則，即三角剖分準則。常用的三角形剖分準則為以下6種：①張角最大準則：一點到基線邊的張角是最大的；②空外接圓準則：就是TIN中過每個三角形的外接圓均不包含點集除了該三角形的頂點之外的任何其他點；③最大最小角準則：每兩相鄰三角形所形成的凸四邊形中，這兩個三角形的最小內角一定大于交換該凸四邊形對角線后新形成的兩三角形的最小內角；④最短距離和準則：即一點到基線邊兩個端點的距離之和是最小的；⑤對角線準則：若是兩三角形組成凸四邊形的兩條對角線之比超過限定閾值時，則需要對三角形進行優化；⑥面積比準則：就是三角形的面積與周長平方之比最小(或者三角形內切圓的面積與三角形的面積之比最小)。在理論上已經證明了張角最大準則、空外接圓準則和最大最小角準則是等價的，但其他的則不是。其中對角線準則受主觀因素影響，已經很少用到。

通常將在空外接圓準則、最大最小角準則下進行的三角剖分稱為Delaunay三角剖分(簡稱DT)。并且空外接圓準則與最小角最大準則是Delaunay三角網的兩個基本性質。實際上，任何三角剖分準則下得到的TIN，只要利用LOP法則(局部優化過程，Local optimal procedure，Lawson于1977年提出)來進行優化處理，都能得到一個唯一的DT三角網。

2.2 設計表面TIN模型的建立

在各種土方工程中，設計表面可以圖形的方式給出，也可以數學函數的形式給出，如場地平整平面，整個區域可有不同的表達式，例如道路設計表面中的左右邊坡、路面等。

若設計表面以數學表達式給出，則地形表面TIN模型和設計表面模型TIN在平面位置上具有相同的三角網形，而在同一平面位置上地面模型與設計模型的高程值不同。但是設計表面TIN模型的高程可由模型的三角形頂點坐標代入到設計表面函數計算得到。設地形表面TIN模型三角形頂點P坐標為(xp，yp)，設計表面函數為HD=g(x，y)，則P點的設計高程為Hd(P)=g(xp，yp)。根據設計表面函數求出每個地形表面三角形頂點所對應的設計高程，則可建立相應的設計表面TIN模型。

若設計表面以圖件形式或散點形式給出，則可先對設計表面建立TIN。但由于地形表面模型和設計表面模型具有不同的三角網形結構。這時要進行數據加密處理，即把設計表面中的點內插到地形表面上，并求出設計表面散點對應的地面高程；同時，將地形表面上的點內插到設計表面中，并求出地形點對應的設計高程。另外，不同的TIN模型上，三角形邊相交處的坐標和高程也相應求出。這樣就建立了具有相同結構的兩個TIN模型。

2.3 土石方量的計算

得到地形表面TIN模型和設計表面模型TIN后，通過疊加產生地形表面與設計表面高程差異，從而在三維空間上形成不同結構的棱柱體。土石方量計算其實就是計算三角棱的體積，通過計算三角網中每個三棱錐柱的填挖方量，再求和得到整個三角網的總填挖土石方量。

根據三角形三個頂點地形高程和設計高程情況，每個三角形區域分為全填全挖或有填有挖兩種情況考慮。當三角形三個頂點的高程都大于(或小于)設計高程。如圖1(a)所示。

(1)

式(1)中：S為三角形投影到水平面的面積；H1，H2，H3分別為三角形三個頂點與設計面的高差(取絕對值)。

當三角形三個頂點的地形高程值既有大于也有小于設計高程。這時設計面將三角形分成兩部分，一部分為底面是三角形的錐體，另一部分是底面為四邊形的楔體。如圖1(b)所示。錐體部分和楔體部分的體積計算公式分別為：

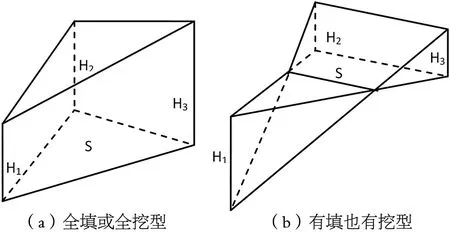
圖1 三角棱柱的體積計算

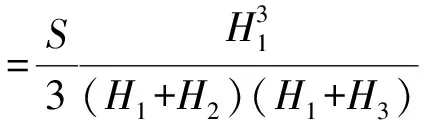
(2)

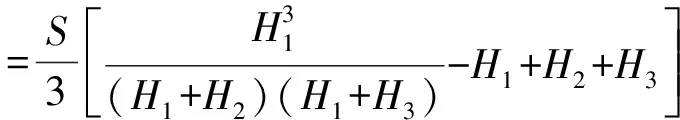
(3)

式(2)和(3)中：S為三角形投影到水平面的面積；H1，H2，H3為三角形三個頂點與設計面的高差(取絕對值)，其中H1恒指錐體頂點與設計面的高差(取絕對值)。另外，有填方也有挖方在實際計算過程中主要分為6種情況考慮，即：①H1<0，H2>0，H3>0；②H1>0，H2<0，H3>0；③H1>0，H2>0，H3<0；④H1>0，H2<0，H3<0；⑤H1<0，H2>0，H3<0；⑥H1<0，H2<0，H3>0。

3 程序實現與實驗分析

3.1 程序實現

為了分析Delaunay三角網法計算土石方的效果，筆者采用三角網生長算法編寫基于Delaunay三角網法計算土石方的程序。考慮到便于對所剖分的離散點集和形成的三角形進行管理，程序設計3個單向鏈表類。它們分別是：①點表類(CPointList)，用于管理的離散點集。參數有點名(PointName)、點號(indexP)、X坐標(x)、Y坐標(y)和Z坐標(z)，還有該點是否為封閉點(closePoint)以及一點所在的圓環號(RingNum)。②邊表類(CEdgeList)，用于管理三角剖分后生成的每一條邊。類的參數有邊號(indexE)、起始點(startPt)、終止點(endPt)和該邊的已被幾個三角形共用(useCount)。其中起始點(startPt)和終止點(endPt)均屬于點表類(CPointList)。③三角形表類(CTriList)，用于管理三角剖分后生成的每一個三角形。類的參數有三角形號(indexT)、三角形的L0邊(L0)、三角形的L1邊(L1)和三角形的L2邊(L2)。其中三角形的L0邊(L0)、三角形的L1邊(L1)和三角形的L2邊(L2)均屬于邊表類(CEdgeList)。其程序實現過程如下：

(1)創建初始三角形

在數據集中找到距幾何中心最近的點A，再找到距A點最近的點B，由點A、B組成第一條基線AB。然后對數據集進行搜索，找到與AB邊有最大夾角的點C，將A、B、C三點按逆時針鏈接形成初始三角形，并且給邊AB(L0邊)、BC(L1邊)、CA(L2邊)的擴展次數(useCount)賦為1。并規定以后每生成一個三角形，都按照逆時針方向鏈接三個頂點。

(2)擴展邊以形成整個區域的無約束Delaunay三角網

有了初始三角形，后面的工作就是開始循環逐步擴展生成三角網，設從第triNum個三角形開始，分別對三角形triNum的三邊L0、L1、L2做如下處理(以L0邊為例)：

①查找可用的頂點。要擴展生成下一個三角形，下一個點必定不是三角形triNum上的點，而且也不是與C點在同一側。

②找出可用點中與邊L0形成夾角最大的那個點。然后與L0兩端點連接完成三角形的一次擴展，并給L0邊的useCount值+1。

分別處理L1、L2邊，并以此循環，直到三角形的個數不再增長，則完成整個數據域的無約束Delaunay三角網生成。

(3)將生成的點表、邊表、三角形表傳遞到繪圖類、土方計算類中。

(4)繪圖類中將每一條邊繪制，連接成網。

(5)土方計算類中，對每個三角形進行計算，最后計算所有三角形的填挖方總和。這里主要有三種情況：僅有填方、僅有挖方和既有填方也有挖方。其中既有填方也有挖方又細分六種情況考慮。

3.2 土石方量計算結果比較分析

為了說明Delaunay三角網法土石方量計算本文方法精度，進行了仿真測試精度分析和實際測量精度分析。

(1)仿真測試精度分析

利用曲面函數構造模型進行測試(圖2)，首先對該函數進行積分計算(本處指定z=0，a=16，b=16，-50≤x≤50，-50≤y≤50)。因為這里指定a=b，所以該曲面是對稱的，當|x|>|y|時z<0，即此時為填方，反之為挖方，且填挖方量相等。而|x|=|y|將區域分成4個部分，4個部分的計算結果絕對值相等：

圖2 雙曲拋物面示意圖

V總=4×V=4×8138.021=32552.084

圖3 劃定雙曲拋物面的測試區域范圍

圖4 函數的三維模型視圖

在CASS7.0中生成三角網，并用DTM法計算土方，如圖5所示。由圖5可以看到，土石方總量=15632.268+15659.817=31292.085，與積分計算得到的結果(32552.084)有3.87%(1259.999方)的偏差。原因在于CASS7.0中三角網不是嚴格的Delaunay三角網，另外CASS生成的三角網的最外層邊連成的多邊形不是嚴格凸的。

圖5 在CASS7.0中用DTM法計算1 009個點的土石方量

同樣采用上面生成的1 009個點數據文件，在基于Delaunay三角網法程序中計算土石方量，如圖6所示。由圖6可以看到，這里土石方總量=16245.10+16274.10=32519.20，與積分計算得到的結果(32552.084)僅有0.10%(32.884方)的偏差。

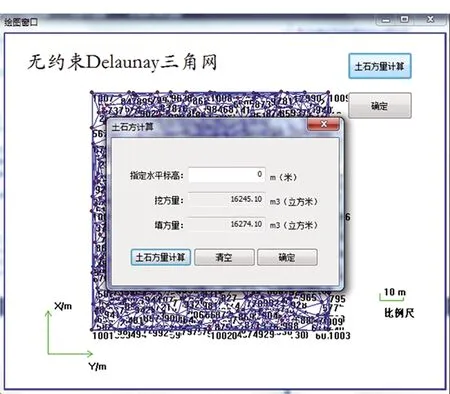
圖6 Delaunay三角網算法下計算1009個點的土石方量

由于該函數對應的曲面是一個光滑曲面，參與計算的隨機點越多，計算得到的土方量與積分結果越接近。為了證明點數與計算結果的精確性的關系，筆者還分別測試隨機生成109個點、509個點和 2 009個點計算的土石方量作為比較的依據(圖7)：

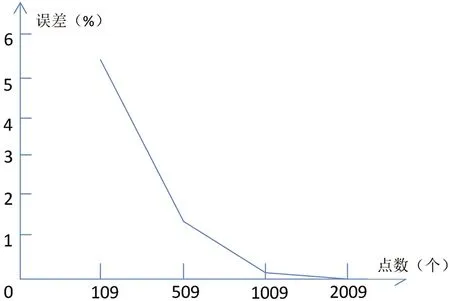
圖7 測點數量與誤差關系圖

①109個隨機點的測試結果為：土石方總量=15223.76+15623.66=30847.42，與積分計算得到的結果(32552.084)偏差5.24%(1704.664方)。

②509個隨機點的測試結果為：土石方總量=16067.79+16060.36=32128.15，與積分計算得到的結果(32552.084)偏差1.30%(423.934方)。

③2 009個隨機點的測試結果為：土石方總量=16265.75+16299.50=32565.25，與積分計算得到的結果(32552.084)僅偏差了0.04%(13.166方)。

通過這幾次測試可以看到，同一個測試區域內，隨著離散點數量的增加，計算得到的土石方量與積分得到的土石方量誤差也越來越小。

(2)實際數據精度分析

為了說明基于Delaunay三角網法計算土石方量本文方法精度，筆者外業采用測繪儀器在野外選取一片地形稍有起伏的區域實地采集了21個點位坐標數據，如表1所示。

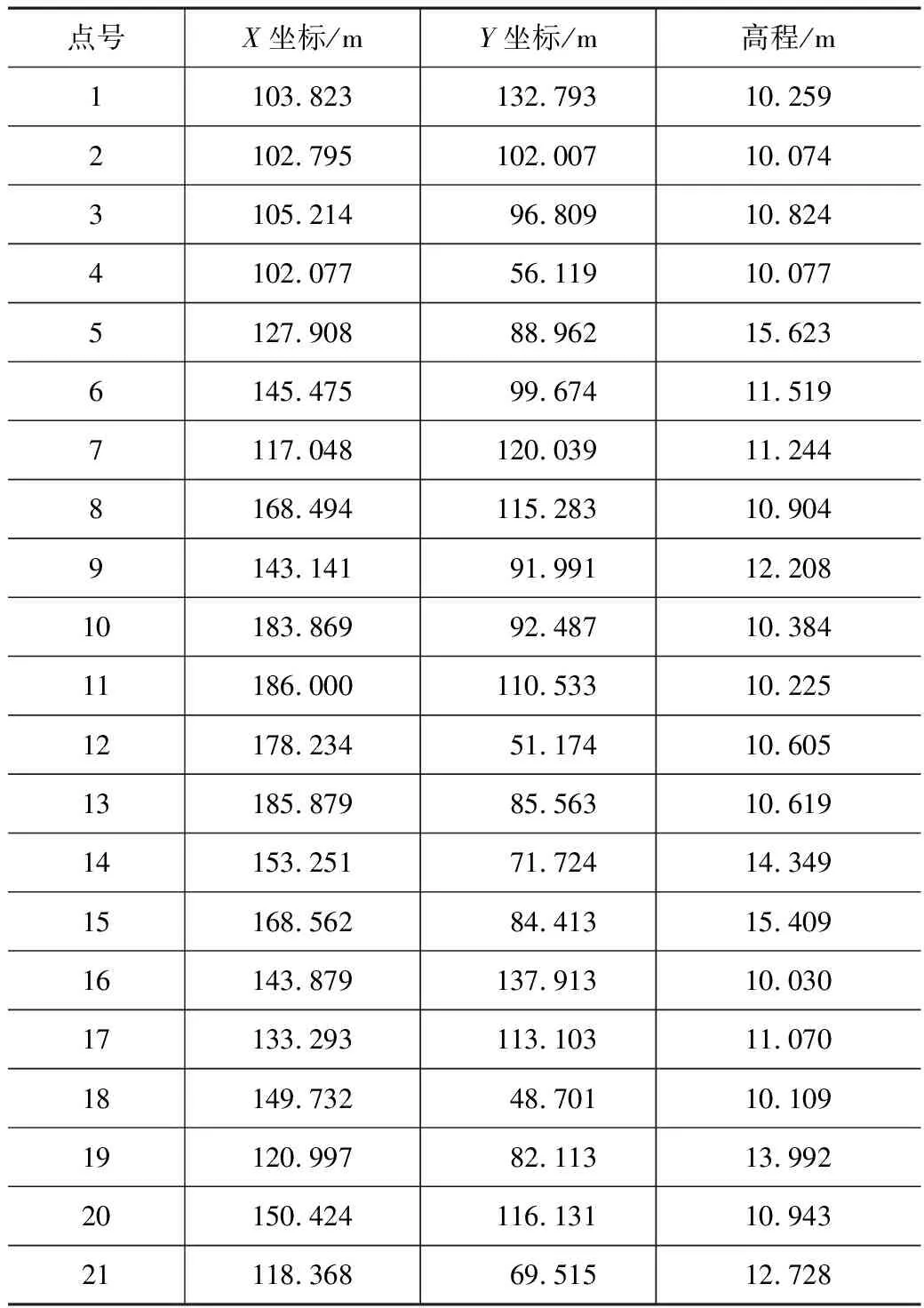
某區域實測數據 表1

內業利用南方CASS7.0生成DTM后計算的土石方量，其結果如圖8所示，本文方法計算的土石方量如圖9所示。

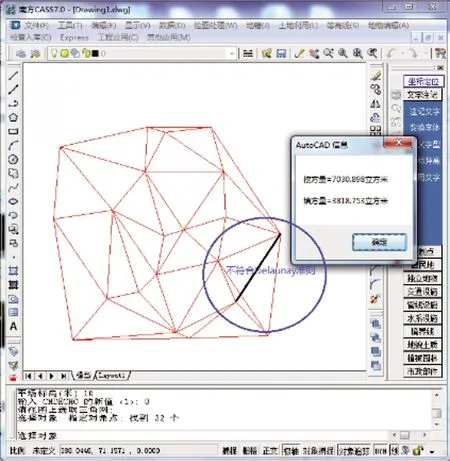
圖8 CASS7.0的DTM法生成的三角網

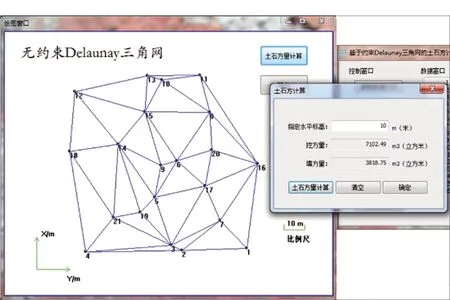
圖9 Delaunay三角網法生成的三角網

由圖8、圖9比較看出：基于Delaunay三角網法計算的挖方量與南方CASS7.0的不同。原因則是由于三角網的網形不相同，CASS7.0生成的三角網不符合Delaunay三角剖分準則(圖8中畫圈的四邊形不滿足空外接圓準則，需要交換對角線)。又根據前文(圖5、圖6對比)證明，本次實際數據測試基于Delaunay三角網法計算的精度更可靠。

4 結 語

本文通過數據測試表明，基于Delaunay三角網法計算得到的土石方量結果相比傳統三角網計算的土石方量有較大精度上的提高，尤其在采樣的數據點不是很密集的時候，表現更為明顯。因此基于Delaunay三角網的TIN模型更接近實際地面模型，計算出的土石方量準確性更高。