絕緣涂層厚度對滾動軸承力學性能的影響研究

馮殿廣，楊錚鑫，黨鵬飛

（沈陽化工大學 機械與動力工程學院，110142，遼寧沈陽）

滾動軸承作為現代機械裝備所必需的關鍵基礎部件，其精度、材質和性能直接影響著機械裝備的使用壽命、可靠性等。在工程應用中，表面涂層技術可以有效改善軸承材料的性能，提高軸承材料的承載能力、可靠性和使用壽命[1]。絕緣涂層的特點有熔點高、硬度大、化學穩定性好、高頻介電損耗小及絕緣電阻率高等，其中Al2O3以優良的表面性能被廣泛用作絕緣材料[2-4]。絕緣軸承在電力行業、鐵路行業、機械行業等領域的設備中，有著至關重要的地位。

絕緣軸承中涂層材料的接觸分析需要使用數值計算的方法，例如有限元法[5-6]、邊界元法[7]和半解析法[8]。有限元法的主要優勢是概念淺顯清晰，易于掌握，描述簡單，應用范圍廣，但需要大量的計算時間。Holmberg等[9]利用有限元法進行了表面涂層的摩擦和斷裂性能分析；浙江大學鄢建輝[10]對TiN、TiC、Si3N4及SiC 四種硬涂層技術體系表面下的應力分布情況進行了研究與模擬數據分析。

基于現有軸承動力學模型，本文建立絕緣軸承模型作為研究對象，采用ABAQUS 有限元軟件進行力學分析，研究模擬基于重力場、徑向載荷和轉速條件的絕緣涂層厚度對于滾動軸承系統接觸應力的影響。結果表明，隨著涂層厚度的增加，絕緣軸承整體Mises 應力值隨之增加。

1 軸承有限元模型的建立

對于絕緣軸承力學分析的有限元建模，建立滾動體-滾道接觸模型是整個動力學接觸建模的關鍵。接觸屬于非線性問題，主要體現在接觸局域的大小、接觸物體間的相互位置關系都是未知的，并且都是變化的。接觸條件的非線性主要內容包括在接觸材料表面法向需要滿足兩物體不相互貫穿、侵入或覆蓋的條件，接觸力法向分量只能是壓力，接觸表面切向摩擦力具有非線性屬性。

1.1 建模的基本原理

ABAQUS/Explicit 中的顯式時間積分采用中心差分法，在前一個增量步基礎上計算下一個增量步。在增量步初始時，程序對動力學平衡方程進行求解，動力學平衡方程為節點的合力等于節點質量m 乘以節點加速度a，即

式中：Fi是結構中的內力，Fe是所施加的外力[11]。

1.2 軸承各零件尺寸參數

本文所使用的絕緣軸承的具體參數見表1，涂覆涂層材料于軸承內滾道外圈、外滾道內圈的結構模型如圖1 所示。

圖1 涂覆涂層材料的軸承結構模型

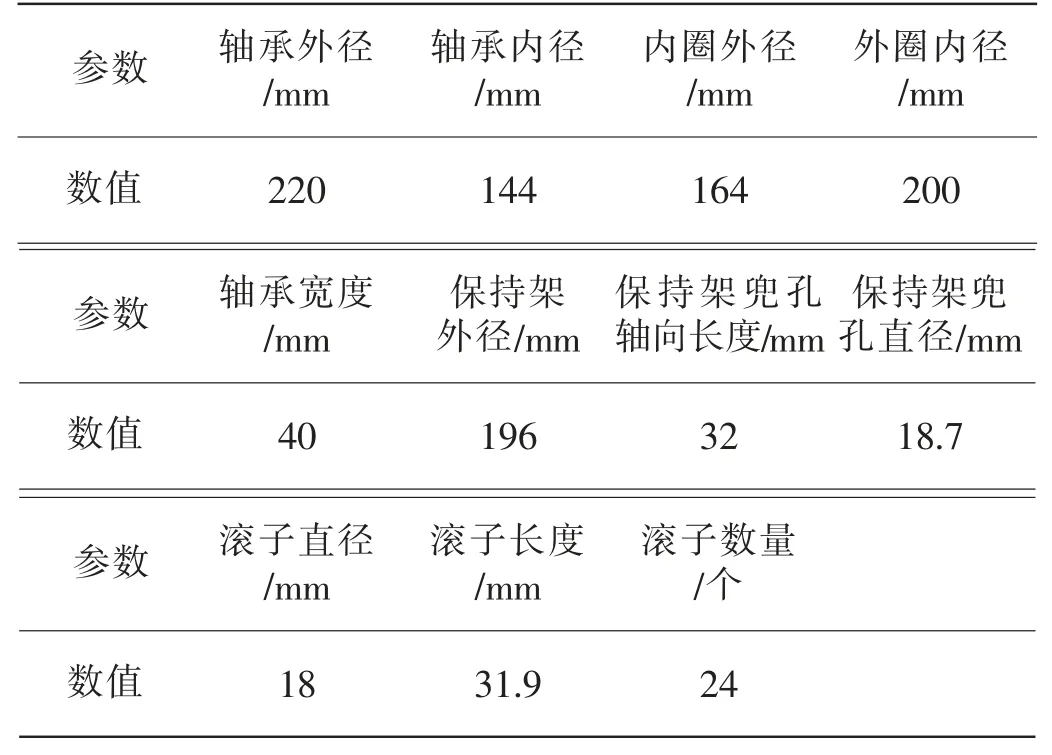
表1 滾動軸承尺寸參數

1.3 材料屬性設置

本文所研究的絕緣軸承的內外圈所使用的材料為高碳鉻軸承鋼GCr15。GCr15 軸承鋼具有均勻的組織、良好的耐磨性、較高的接觸疲勞性能和硬度、較低的摩擦因數，能夠滿足軸承的使用性能要求。涂覆于滾動軸承內滾道外圈和外滾道內圈的絕緣涂層材料為Al2O3。Al2O3熱穩定性好，化學性質穩定，具有較大強度，能在很大壓力梯度下操作，而不會被壓縮和蠕變，以優良的性能被廣泛用作絕緣材料。滾動軸承基體及涂層材料具體參數如表2 所示。

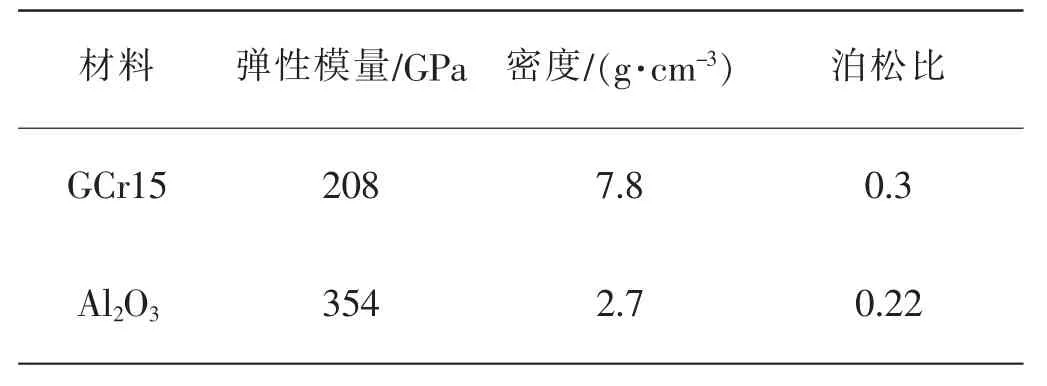
表2 軸承基體及涂層材料

1.4 網格屬性

網格劃分是仿真分析前處理中十分重要的一步，其質量和類型直接影響仿真結果的準確性。在劃分網格之前，首先要選擇合適的網格單元類型和合理的網格大小。本文建立的絕緣軸承動力學有限元模型，由于保持架結構過于復雜，所以采用二次四面體C3D10M網格單元，絕緣軸承剩余各零件采用C3D8R 網格單元。與其他單元相比，C3D8R 單元具有明顯優點，在彎曲荷載下不易發生剪切自鎖，位移計算結果比較精確，當網格發生變形時，分析結果的準確性不會受到很大的影響。

1.5 載荷及邊界條件設置

絕緣軸承動力學模型主要有三個分析步：在分析步Step-1 中進行重力加載，保證各零件接觸；在分析步Step-2 設置為向-Y 方向施加20 kN 徑向載荷；在分析步Step-3 設置為在內圈施加2 000 r/min 轉速。

在建立的絕緣軸承模型中心處設置兩個參考點，分別將絕緣軸承的內圈和保持架進行耦合。根據實際工況，在進行有限元仿真分析時采用軸承外圈固定、軸承內圈旋轉的運動方式，所以施加的邊界條件為限制軸承外圈外表面所有轉動和移動的自由度，軸承內圈及保持架限制3，4，5，6 方向的自由度。在分析步Step-3 時，同時釋放軸承內圈和保持架6 方向的自由度，給軸承內圈施加繞軸線方向的轉速。設置滾動軸承接觸屬性為通用接觸，法向采用“硬”接觸，切向行為設置為靜摩擦-動摩擦指數衰減，這里靜摩擦系數為0.1，動摩擦系數為0.05，衰減系數為0.01。

2 有限元仿真結果

在20 kN 徑向載荷和2 000 r/min 轉速工況下，不同涂層厚度下絕緣軸承Mises 應力圖如圖2～4 所示，詳細計算結果如表3 所示。比較不同涂層厚度下絕緣軸承整體最大應力值，隨著涂層厚度的增加，絕緣軸承整體的最大應力值也隨之增加，在0.075 mm 涂層厚度時達到最大值。

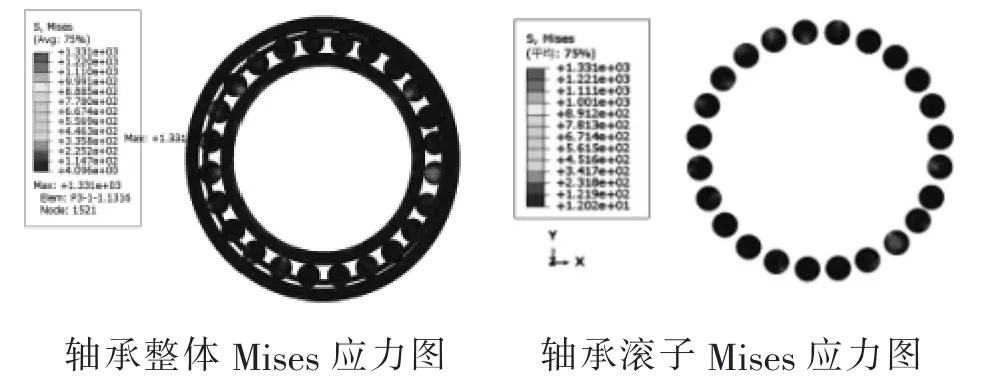
圖2 0.025 mm 涂層厚度下絕緣軸承Mises 應力圖

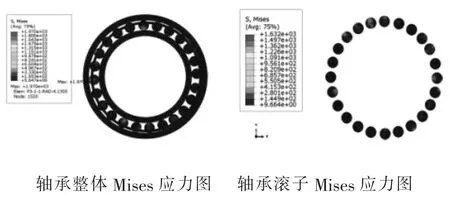
圖3 0.05 mm 涂層厚度下絕緣軸承Mises 應力圖

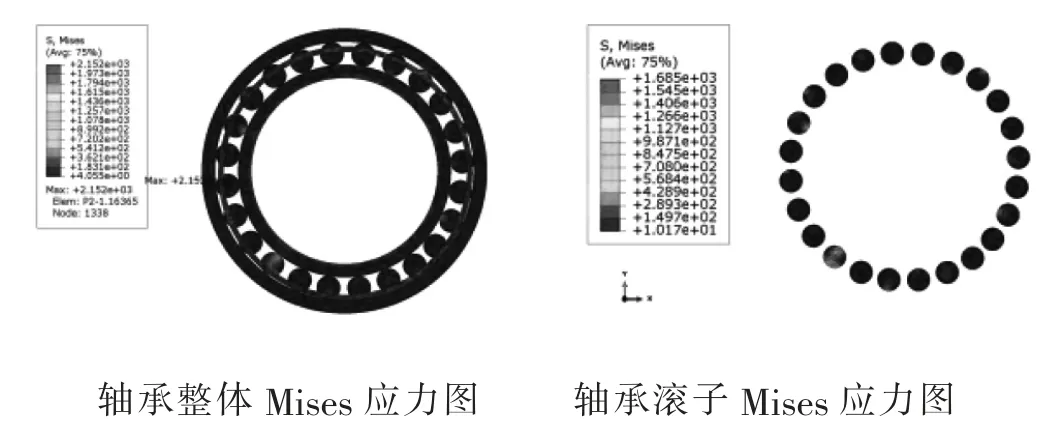
圖4 0.075 mm 涂層厚度下絕緣軸承Mises 應力圖

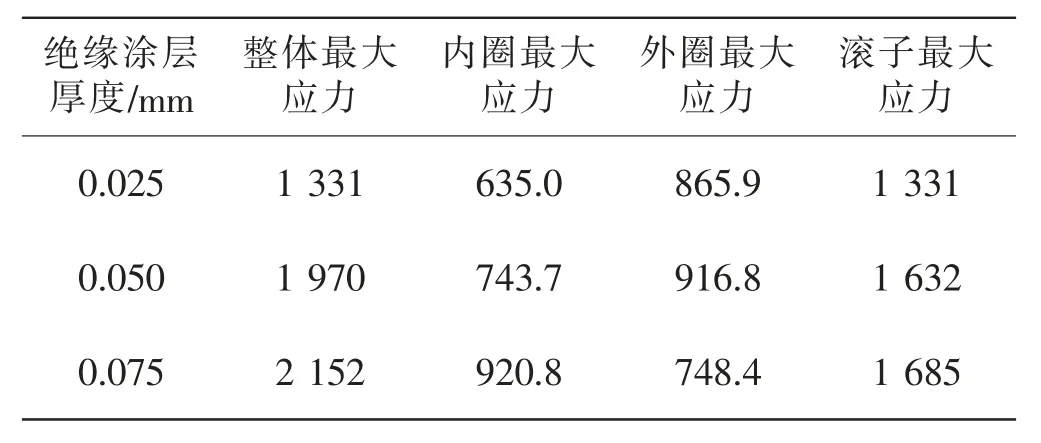
表3 不同絕緣涂層厚度最大Mises 應力值 MPa

根據表3 可以看出：0.025 mm 涂層厚度時，絕緣軸承內圈最大應力值最小，絕緣軸承內圈最大應力值隨著涂層厚度的增加，整體呈上升趨勢；0.075 mm 涂層厚度時，絕緣軸承外圈最大應力值最小，絕緣軸承外圈最大應力值隨著涂層厚度的增加，整體呈下降趨勢；0.075 mm 涂層厚度時，絕緣軸承滾子最大應力值最大。

3 結語

（1）本文建立了絕緣軸承動力學模型，開展絕緣涂層厚度對滾動軸承力學性能影響的研究，獲得了不同絕緣涂層厚度下軸承整體應力的變化趨勢。

（2）基于本文模擬的三種涂層厚度的絕緣軸承，在涂層厚度為0.025 mm 時，絕緣軸承整體Mises 應力最小；在涂層厚度為0.075 mm 時，絕緣軸承整體Mises應力最大。隨著涂層厚度的增加，軸承整體Mises 應力值隨之增加。

（3）絕緣軸承內圈最大應力值隨著涂層厚度的增加，整體呈上升趨勢；絕緣軸承外圈最大應力值隨著涂層厚度的增加，整體呈下降趨勢；0.075 mm 涂層厚度時，絕緣軸承滾子應力值最大。