基于自適應卡爾曼濾波法的懸臂施工撓度控制

張付林，汪 東，景 浩，王銀輝，肖廣良

（1.寧波市軌道交通集團有限公司，浙江 寧波 315101；2.中鐵四局集團有限公司，安徽 合肥 230023；3.浙大寧波理工學院土木建筑工程學院，浙江 寧波 315100）

0 引 言

連續剛構橋的成橋過程是一個復雜的系統工程，需要經歷多個施工階段，且在成橋后結構線形和內力難以調整，理想成橋狀態的實現需要施工過程結構狀態按照既定的軌跡發展。然而，施工過程中結構的實際狀態和理想狀態仍會因施工誤差、測量誤差、模型誤差、預應力松弛，以及與時間相關的收縮徐變等因素影響，而不可避免地存在偏差。因此，如何準確把握橋梁結構施工過程中的力學行為、修正和降低結構的施工誤差成為橋梁施工控制的重中之重。

目前，橋梁施工控制方法主要有開環控制、閉環控制和自適應控制三種[1]。其中，閉環控制逐漸采用卡爾曼濾波、人工神經網絡、最小二乘法等系列理論來獲得結構的真實撓度并進行控制。例如，金塘大橋西通航孔橋[2]施工中采用卡爾曼濾波法對結構預拱度進行預測。梁濟運河大橋[3]應用卡爾曼濾波法預測連續剛構橋的立模標高。三灘黃河大橋[4]運用人工神經網絡進行橋梁施工過程預拱度的預測。渭河特大橋[5]運用最小二乘法對混凝土彈性模量、預應力張拉力、混凝土容重進行參數識別、修正，并在此基礎上運用灰色理論進行撓度預測。黑垅大橋[6]首先采用最小二乘法對模型仿真理論所取參數值進行調整，然后利用灰色系統理論進行撓度預測。上述案例監控結果均表明，所采用的閉環控制理論均取得了良好的控制效果。然而，卡爾曼濾波理論的濾波效果很大程度依賴于對噪聲統計特性的評估。準確評估噪聲統計特性對采用卡爾曼濾波理論進行施工控制具有重要意義。

鑒于此，本文采用自適應卡爾曼濾波理論進行橋梁施工控制。在利用對觀測數據進行濾波的同時，實時地對未知的或不確切的系統模型參數和噪聲的統計特性進行適當的估計和修正，以補償濾波中對動態噪聲統計特性估計的不足。此外，為保障橋梁結構線形平順或相鄰節段不出現大折角，提出了每次僅調整立模誤差一半的施工誤差修正策略。本文結合實際工程的應用，證實該方法具有良好的適用性，并為同類橋梁的施工監控提供借鑒。

1 工程概況

寧波市軌道交通4 號線上跨杭深、蕭甬鐵路工程跨鐵路節點橋是一座集大跨、小曲率半徑、不對稱和轉體施工于一體的預應力混凝土連續剛構橋，橋位上行線路中心線曲率半徑為350 m，全長301 m，橋跨布置為（68+138+95）m，如圖1 所示。橋梁上部結構采用懸臂澆筑施工工藝在平行鐵路線兩側澆筑，懸臂施工完成后再轉體合龍施工。橋跨采用不對稱布置形式，轉體T 構懸臂長度分別為50 m（27 號T 構）和86 m（28 號T 構），主梁截面頂板寬11 m，底板寬7 m，27號墩T 構（小T 構）主梁梁高5～9 m（按1.8 次拋物線變化）；28 號墩T 構（大T 構）主梁梁高5～12 m（按1.8 次拋物線變化）。

圖1 立面布置圖（單位：m）

2 立模標高的確定

采用懸臂施工工藝的連續剛構橋任一節段標高受該節段及其后續節段施工的影響而不斷改變，直至成橋狀態。立模標高的控制目標就是使節段標高沿著理想軌跡線到達理想成橋狀態，即通過立模標高的調整使節段標高盡可能接近理想軌跡線。由此可見，立模標高需要抵消后續施工過程（包含本節段）所產生的撓度，即：

式中：HL為立模標高；HD為設計標高；HC為理論預拱度；HG為掛籃變形預拱度。

掛籃變形主要根據掛籃預壓試驗進行計算，并可根據懸臂施工前幾個節段澆筑變形小、掛籃變形為主的特點對掛籃變形預測進行修正。橋梁結構實測撓度與理論撓度不可避免地會存在偏差，可運用現代控制理論，分別建立撓度預測模型對下一施工節段各項撓度進行預測，進而修正立模標高。

為保障橋梁結構線形平順或相鄰節段不出現大折角，每次調整立模誤差的一半，如圖2 所示。

圖2 立模誤差調整示意圖

圖2 中HG（k-1）、HG（k）、HG（k+1）為理論立模標高誤差值，理想狀態為0。H'G（k-1）、H'G（k）為掛籃實際立模誤差值，往往通過澆筑前掛籃立模標高的復測獲得。ΔHG（k-1）為立模誤差導致的調整值。H'G（k+1）為保證結構線形不受立模誤差影響需要的掛籃立模誤差調整值。lk、lk+1 分別為第k、k+1 節段的長度。

3 基于卡爾曼濾波的撓度預測理論

3.1 基于離散線性系統的卡爾曼濾波理論

卡爾曼濾波法的實質是從含噪聲（測量誤差、施工誤差等）的信號中提取出真實信號，估計系統的真實狀態。再用估計出的結構狀態變量，按照確定的規律對結構的后續響應進行預測，對已施工k節段和待施工k+1 節段建立基本離散線性系統狀態方程和測量方程為：

式中：x（k）為k施工步驟時的n維狀態向量，由n個待辨識的結構參數組成；z（k+1） 為k+1 施工步驟時的m維觀測數據向量，由m個觀測數據組成；ω（k）為n維系統隨機干擾向量，代表了狀態方程的污染；v（k+1）為k+1 施工步驟時的m維量測噪聲向量；?（k+1，k）為n×n階狀態轉移矩陣；H（k+1）為k+1施工步驟時從x（k+1）到z（k+1）的m×n維線性變換矩陣。

基于卡爾曼濾波系統的噪聲的統計特性為：

其中：

Rk為m×m 維正定對角矩陣，其每個元素為相應矩陣行的觀測變量的均方差，即Rk為測量誤差均方差。

狀態向量的初始統計特性是已知的，即：

線性離散型系統的最優線性估計問題可表示為：給出控制系統的狀態方程和觀測方程，給出觀測序列z（0），z（1），z（2），…，z（j），要求線性最小方差估計方法找出的最優線性估計值x?（k）。

在已知的初始條件下，卡爾曼濾波的遞推公式如式（7）～式（10）所示：

從式（10）可見，k+1 時刻的最佳濾波x?（k+1，k+1）等于基于前k次測量z（k）對k+1 時刻的最佳預報x?（k+1，k+1），再加上第k+1 次測量所帶來的信息的加權修正，即K（k+1）[z（k+1）-H（k+1）?（k+1，k）x?（k，k）]，整個濾波遞推的順序是（7）→（8）→（9）→（10）。

3.2 基于自適應卡爾曼濾波法的撓度預測

值得注意的是，標準離散線性卡爾曼濾波假定了系統誤差和量測誤差屬于統計特性已知的獨立高斯隨機系列，即均值為零，自協方差分別為Q（k）和R（k）。這些條件往往存在于理論階段，在T 構懸臂施工線形控制上難以滿足，兩誤差的統計特性實際上是難以知曉的。此外，施工控制過程是一個動態過程，如果其動態噪聲的方差、協方差估計誤差較大，也容易使結果發散。因此，學者們在此基礎上發展了自適應卡爾曼濾波法。

基于自適應卡爾曼濾波法的撓度預測主要用于懸臂施工過程主梁因掛籃前移、混凝土澆筑和預應力張拉引起的撓度偏差的預測上，因此，可建立懸臂端撓度的狀態方程和量測方程：

式中：ω（k）為k施工階段的施工誤差；v（k）為k施工階段的撓度測量誤差；z（k）為k施工階段撓度測量值；x（k+1）為待施工階段k+1 梁端撓度值；x（k）為已完成施工階段k梁端撓度值；?（k+1，k）為線性變換系數，也就是線性變換系數，也就是k+1 階段與k階段懸臂端撓度理論值之比，即：

自適應卡爾曼濾波的噪聲統計特性為：

式中：q（k）和r（k）分別為系統噪聲和觀測噪聲的均值，其余同式（4）。

由于量測誤差均值不為零，故相對于式（1），真實撓度狀態的濾波估計值為：

濾波增益矩陣為：

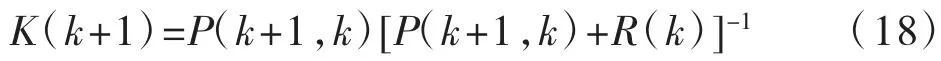
預測誤差協方差矩陣為：

濾波誤差協方差矩陣為：

在系統誤差和量測誤差的傳遞過程中引入了遺忘因子b（0＜b＜1），通過b的取值起到限制濾波的記憶長度，增加新近監測數據對當前估計的作用。相應的系統誤差和量測誤差的傳遞關系為：

一般而言，混凝土連續剛構橋懸臂施工過程前期，結構變形很小，相應的撓度偏差也很小，因此一般選擇施工至某一節段作為自適應卡爾曼濾波的初始時刻。相應地選取x?（0）為該節段施工的理論撓度，P（0，0）為該節段施工理論撓度與實測撓度差值的平方，Q（0）為初始階段系統誤差的均方差，R（0）為測量誤差均方差，遺忘因子b根據經驗一般取0.7。

根據以上取值，可按照（19）→（18）→（20）→（17）→（16）→（15）→（21）→（22）→（23）→（24）→（25）→（19）→（18）……的順序計算出已施工節段的撓度真實值和下一節段撓度的預測值及各種參數值，從而實現待施工梁段撓度的預測。

4 主梁撓度控制結果分析

混凝土連續剛構橋主梁剛度隨懸臂長度的增大而減小，當懸臂長度較短時，結構剛度大、變形小，混凝土澆筑導致的懸臂端下撓變形主要由掛籃變形引起，張拉變形主要受測量誤差的影響，結構的實際標高偏差主要來源于立模誤差和掛籃變形估計偏差。當懸臂長度增長時，結構剛度減小、變形增大，主梁受力變形逐漸占主導因素。因此，懸臂施工前期，應進行掛籃變形、測量誤差等分析，立模標高的控制主要針對立模誤差展開；懸臂施工后期，應在前期的基礎上進行撓度的預測和控制，立模標高的控制主要針對結構理論撓度與實際變形的誤差展開。本文針對前六個節段的監測主要進行掛籃變形規律和測量誤差特性的分析，并根據立模誤差進行立模標高的修正；后續節段根據前六個節段的監測成果進行掛籃變形的修正、撓度的預測和立模標高的修正。受實際工程進度的影響，依托項目施工至28# 墩5 號節段，故僅展示以上節段的施工監控成果。各節段施工后梁底實測標高如圖3 和圖4 所示。各施工節段撓度監測值如表1 所示。

圖3 28# 墩邊跨側主梁梁底標高

圖4 28# 墩中跨側主梁梁底標高

由圖3 和圖4 可以看出，實際結構梁底標高略高于理論標高，主要原因是施工1# 和2# 節段時存在較大的立模誤差。兩側梁底標高隨懸臂的伸長逐漸接近理論標高，5# 節段邊跨側梁底標高比理論標高高6 mm，中跨側高4 mm，且保證了橋梁線形的整體平順。由此可以看出，針對立模誤差所采用的立模標高調整方法達到了較好的控制效果。

由表1 可以看出，懸臂端實測撓度值與理論變形值較接近。根據依托項目結構變形特點，主梁在前五個節段澆筑過程中懸臂前端受力變形值很小，均小于1 mm，澆筑階段懸臂前端的撓度主要來源于掛籃的彈性變形，因此可以看出掛籃變形值與理論值較為接近，平均誤差在3 mm 以內。根據掛籃預壓試驗結果，較好地估計了掛籃變形值。前五個節段預應力張拉變形理論值為0 mm，其實測值與之相差約為1 mm，該差值主要來源于測量誤差。

表1 28# 墩各施工階段懸臂端撓度值 單位：m

5 結 論

（1）連續剛構橋施工過程可調變量主要是立模標高，立模誤差離散性大。為保證結構的線形，需要進行單獨的修正。卡爾曼濾波法可以從被噪聲污染的撓度實測數據中識別出系統真實狀態，并進行撓度預測，可用于彌補自適應控制法部分狀態參數難以辨識所帶來的誤差。

（2）橋梁懸臂施工前期各節段標高誤差主要來源于立模誤差，以橋梁結構線形平順為原則，通過每次調整立模誤差一半的手段，經過多個節段的逐步調整，使節段標高回歸至設計位置，且保證了主梁線形的整體平順。

（3）澆筑和張拉階段懸臂端撓度的實測值與理論值接近，懸臂施工前期澆筑變形主要來源于掛籃變形，掛籃預壓試驗結果得到的掛籃變形估計值與實測值吻合較好。

（4）寧波市軌道交通4 號線上跨杭深、蕭甬鐵路工程跨鐵路節點橋實例計算證明了該方法的實用性和有效性.