例談導數求解函數單調性的類型及策略

云南 馬孟華 趙寅輝

隨著高考改革的不斷深入，全國高考數學文、理卷(包括2021年不分文理的新高考Ⅰ，Ⅱ卷)中對導數的考查成為了重點、熱點問題，也是高考中區分度高、難度較大的題目.縱觀近年來高考數學中對導數的考查，往往以壓軸題型登場，其考點主要集中在以下幾個方向：(1)導數幾何意義的應用(研究函數圖象的切線問題)；(2)導數在研究函數的單調性、極值、最值上的應用；(3)導數在研究函數零點、方程的根問題上的應用；(4)導數在研究函數不等式恒成立、有解、證明不等式成立問題上的應用等.在上述考查方向的背景下，在函數中“引入參數”，就會使得問題變得更加復雜和困難，故也使問題有了較大的難度和區分度，這也是導數常常作為壓軸題登場的原因之一.

下面以“導數的應用”為背景，從“導數求解函數單調性”問題的幾類模型出發，提出利用導數解決函數單調性的系統方法.旨在引領考生攻克高考常考考點及重難點問題，為2022年高考備考提供指引和幫助！

1.類型一：直接求解型

此類模型主要適用于函數中不含參數，且求導后的“導數不等式”可直接求解，一般這類模型問題比較簡單，如：

【例1】(2021·新高考Ⅰ卷·22(Ⅰ))已知函數f(x)=x(1-lnx).

(Ⅰ)討論f(x)的單調性.

【解析】f(x)的定義域為(0,+∞)，

又f′(x)=1-lnx-1=-lnx，

令f′(x)>0，得x∈(0,1)；

令f′(x)<0，得x∈(1,+∞).

故f(x)在(0,1)上單調遞增，在(1,+∞)上單調遞減.

【評析】對函數求導之后，對應導函數大于(小于)0的不等式可直接求解，求出函數的單調區間，但需要注意定義域的限制.

2.類型二：“逆向”求解型

此類模型是針對函數求導后不等式難以“直接求解”(如：導函數不等式屬于超越不等式類型或導函數含參數)或無法求解時，可借助導函數的“零點”將函數定義域分為若干區間，在每一個區間上討論導函數的正負性，進而求解出原函數的單調性.如：

【例2】已知函數f(x)=ex-ln(x+m).

(Ⅰ)設x=0是f(x)的極值點，求m并討論f(x)的單調性.

2.1 “逆向討論”策略

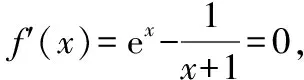
所以f(x)在(-1,0)上單調遞減，在(0,+∞)上單調遞增．

2.2 “數形結合”策略

當x∈(-1,0)時，f′(x)<0，當x∈(0,+∞)時，f′(x)>0，

故f(x)在(-1,0)上單調遞減，在(0,+∞)上單調遞增.

【評析】從方法二可以看到，2.1中的逆向討論法在特定情形下，也可使用數形結合的方式討論導函數的正負性，從而避免了分析導函數中各個構成函數的正負性問題，直接從圖形上觀察得到了在定義域內的不同區間上導函數正負性問題.事實上，兩類方法的理論基礎都建立在函數零點、方程的根以及函數圖象交點的等價關系上.

同時，我們注意到，在不能直接求解導數不等式的背景下，引入“令f′(x)=0”這一方法，先來討論導函數的零點(函數f(x)可能的極值點)，再通過“逆向討論法”或“數形結合”的方式就可快速解決函數的單調性求解問題，這是最為有效的方法，也是通性通法.

3.類型三：含參數的函數單調性討論

當導函數中含有參數，且該參數影響導函數的零點個數以及正負性時，需要帶著參數對導函數的影響進行討論，這種類型的單調性討論往往伴隨著參數的影響而難以求解，下面介紹利用“導函數的零點討論法”求解此類問題.

3.1 含參函數的導函數為可因式分解型的求解策略

2021年高考中對此類問題的考查最為突出，下面來看例3.

【例3】(2021·新高考Ⅱ卷·22(Ⅰ))已知函數f(x)=(x-1)ex-ax2+b．

(Ⅰ)討論f(x)的單調性；

【解】(Ⅰ)由函數的解析式可得f′(x)=x(ex-2a)，令f′(x)=0，即x(ex-2a)=0.

故有x=0或ex=2a，

【注】下面分析方程ex=2a是否有解，以及有解后與另一解x=0的大小關系，這就是對參數a如何進行討論的“切入點”.

①當a≤0時，ex=2a無解，此時ex-2a>0，

故當x∈(-∞,0)時，f′(x)<0,f(x)單調遞減，

當x∈(0,+∞)時，f′(x)>0,f(x)單調遞增；

②當a>0時，ex=2a的解為x=ln2a，故討論f′(x)=0的兩解：x=0與x=ln2a的大小關系，

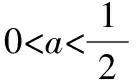
若x∈(-∞,ln2a)，則f′(x)>0,f(x)單調遞增；

若x∈(ln2a,0)，則f′(x)<0,f(x)單調遞減；

若x∈(0,+∞)，則f′(x)>0,f(x)單調遞增；

若x∈(-∞,0)，則f′(x)>0,f(x)單調遞增；

若x∈(0,ln2a)，則f′(x)<0,f(x)單調遞減；

若x∈(ln2a,+∞)，則f′(x)>0,f(x)單調遞增.

【評析】此題出現了導函數的零點討論，討論的“切入點”就是導函數方程“f′(x)=0”的解的個數及大小關系.通過對導函數的因式分解可以得到：導函數的零點一個是“定點”，一個是“動點”(含參數)，故可以通過分析“動點”與“定點”的三種位置關系(即ln2a<0，ln2a=0，ln2a>0)來找到討論單調性的“切入點”，這樣的“討論依據”既可以做到對參數的討論“有理有據”“不重不漏”，又具有較強的邏輯性，再結合2.1,2.2的處理方法即可在含參數的背景下直接求出函數的單調區間，這是高考中對含參函數單調性考查的重難點.

3.2 含參函數的導函數為不可因式分解型的求解策略

【例4】已知函數f(x)=ax3+3x2+3x(a≠0)．討論f(x)的單調性；

【解析】f′(x)=3ax2+6x+3，令f′(x)=0，即3ax2+6x+3=0，其判別式為Δ=36(1-a)，

①Δ=36(1-a)≤0時，即a≥1時，f′(x)≥0恒成立，故f(x)在(-∞,+∞)上單調遞增；

【注】此處Δ=0時，雖然f′(x)=0有一解，但該解不是函數f(x)的極值點，故可以與Δ<0合并討論.

②當Δ=36(1-a)>0時，即a<1時，f′(x)=0有兩根，分別為x1,x2，不妨設

【注】此處先利用判別式Δ討論f′(x)=0的根的情況，在確定了二次方程f′(x)=0根的個數之后，進一步確定二次函數的開口方向，從而清晰地得出原函數的單調區間，故此時應將a<1分為a<0和0

故可得x1<0,x1

當x∈(-∞,x1)∪(x2,+∞)時，f′(x)<0；

當x∈(x1,x2)時，f′(x)>0,

所以f(x)在(-∞,x1)和(x2,+∞)上單調遞減，在(x1,x2)上單調遞增.

得x1<0，x2

當x∈(-∞,x2)∪(x1,+∞)時，f′(x)>0；

當x∈(x2,x1)時，f′(x)<0,

所以f(x)在(-∞,x2)和(x1,+∞)上單調遞增，在(x2,x1)上單調遞減.

綜上所述，當a≥1時，f(x)在(-∞,+∞)上單調遞增；

【評析】例4與例3不同之處在于導函數對應的零點不能直接求出，即導函數不可因式分解，從而難以求出零點，需借助二次方程的求根公式.同時在參數的影響下，還需考慮導函數零點的大小關系，綜合使用數形結合、分類討論的數學思想進行綜合分析討論才能求解出函數的單調區間.從求解過程可以看出：導函數為含參數的二次型函數不可分解因式，可先根據判別式Δ的正負性來對二次方程的根的個數展開第一次討論；在確定了二次方程的根的個數的情況下，對二次函數的開口方向進行第二次討論；在二次方程有兩根的情況下，需討論兩根大小關系進行第三次討論，即可總結為“先Δ，后開口，最后比根大小”的討論模式.這樣的逐級先后對參數討論會使討論依據和切入點非常直觀，并且討論過程不重不漏，邏輯層次清晰，易于理解和掌握.

4.導數求解函數單調性策略的系統總結

導數作為求解可導函數單調區間的“神器”，其重心落在了求解導數大于(小于)0的不等式上.如果導數不等式可直接求解，則問題較為簡單;若導數不等式無法直接求解，則需借助“導函數的零點”(即先處理f′(x)=0是否有解問題，再處理f′(x)>0和f′(x)<0不等式問題)作為“切入點”，尤其含有參數討論函數單調性問題時，這種思維方法能夠引領學生迅速找到分類討論的突破口，從而不重不漏的在參數影響下解決函數的單調性問題.

結合對以上例子的分析以及求解策略的各自特點，我們可以總結得到利用導數求解函數單調性的系統方法：

(1)當導函數中不含參數時，可歸納為以下求解步驟：

①求函數f(x)的導函數f′(x)；

②觀察f′(x)>0(<0)是否可以直接求解，若能，直接求出函數f(x)的單調區間；若不能轉入下一步；

③令f′(x)=0.

(ⅰ)若方程無解，則f′(x)在其定義域上恒大于(恒小于)0，即f(x)在其定義域上恒增或恒減；

(ⅱ)若方程有解，則在定義域范圍內討論這些解(導函數的零點)左、右區間上的導函數f′(x)的正負性(或采用數形結合觀察圖象討論f′(x)的正負性)，進而求出函數f(x)的單調區間，這種方式也稱為“逆向討論法”，即利用導函數的零點將函數定義域分開，再討論不同區間上的導函數的正負性，進而求出各區間上函數f(x)的單調性.

(2)當導函數中含參數時，可歸納為以下步驟：

①求函數f(x)的導函數f′(x)，令f′(x)=0，考慮f′(x)=0的解是否受到參數影響，若參數取值不影響f′(x)=0的解，則直接求出單調區間;若影響，轉為第二步；

②求出f′(x)=0在其定義域內的所有解.

(ⅰ)若f′(x)=0有一解，則在定義域范圍內分析該解左、右兩側導函數的正負性即可求出單調區間；

(ⅱ)若f′(x)=0有兩解，則討論這兩解(含參數)的大小關系，這是討論的“切入點”，一般有三種大小關系，在兩解位置關系確定的情況下，參數的取值范圍也就被確定了，進而再利用“逆向討論法”求出單調區間；