利用k近鄰區間距離的異步抗差航跡關聯算法

衣 曉, 曾 睿,2,*, 曹昕瑩

(1. 海軍航空大學航空作戰勤務學院, 山東 煙臺 264001; 2. 中國人民解放軍92325部隊, 山西 大同 037001)

0 引 言

在分布式多目標跟蹤融合系統中,一個重要問題是如何判斷來自于不同局部節點的航跡是否源自同一目標,即航跡關聯問題。然而傳感器系統誤差的存在增大了航跡關聯的難度,使得系統誤差下的航跡關聯問題與誤差配準問題互為前提。

為克服系統誤差的影響,文獻[8]通過牛頓算法優化標準函數,提出一種最小二乘配準算法;文獻[9]根據同源航跡距離向量相似特征,提出基于最小平均距離的粗關聯和基于分布的精關聯算法;文獻[10]通過推導等價量測方程,基于距離分級聚類實現航跡關聯,在目標密集等復雜環境下能保持很低的錯誤關聯率,穩定性較強。以圖像匹配原理為基礎,將系統誤差的影響轉化為旋轉量和平移量,利用Fourier變換或Radon變換,文獻[17]和文獻[18]提出了一種不依賴于準確誤差配準的航跡關聯技術。文獻[19]利用模糊綜合決策思想,建立模糊因素集,依據航跡緊密度建立矩陣得到有效航跡關聯對來實現系統誤差下的航跡關聯。文獻[21]以目標的拓撲統計距離信息為基礎,進行全局最優關聯,根據雙門限準則完成關聯判決。上述算法的前提均是航跡同步,若航跡異步則需要時域配準,將異步航跡轉換為同步航跡進行處理,但時域配準會導致航跡數據的誤差傳播積累,影響航跡關聯算法的性能。

針對系統誤差難以描述的問題,提出兩種系統誤差區間化方法,把帶有系統誤差的航跡數據轉換成區間數進行處理。給出區間序列到區間點的近鄰區間距離計算規則,通過不等長航跡區間序列間的相似度,實現了航跡異步和系統誤差下的同時關聯。本文算法可有效降低系統誤差對關聯結果的影響,并且無需時域配準,可對異步不等速率航跡直接關聯。

1 區間序列的相似度度量

區間坐標序列與區間坐標點的近鄰區間距離

設非空區間坐標序列為

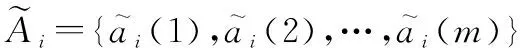
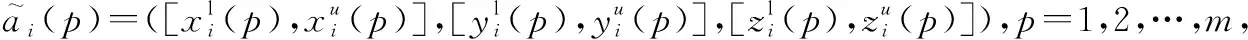
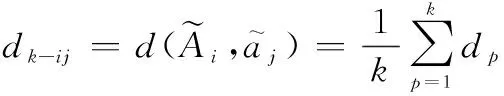
(1)

不等長區間坐標序列間的相似度

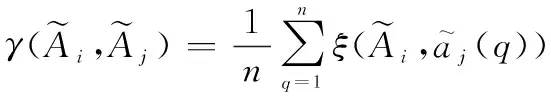
(2)

式中:

(3)

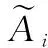
定義1、定義2中坐標變量均為三維坐標,適用于三維空間;對于二維情況,只需相應變更坐標變量維數即可。

2 利用k近鄰區間距離的航跡關聯算法

2.1 問題描述

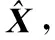
單側區間化:假設局部節點傳感器的系統誤差偏差方向已知,即Δ∈(0,Δ),Δ∈(0,Δ),則在不考慮量測隨機誤差的條件下,觀測值與真值滿足:

(4)

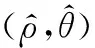
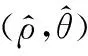
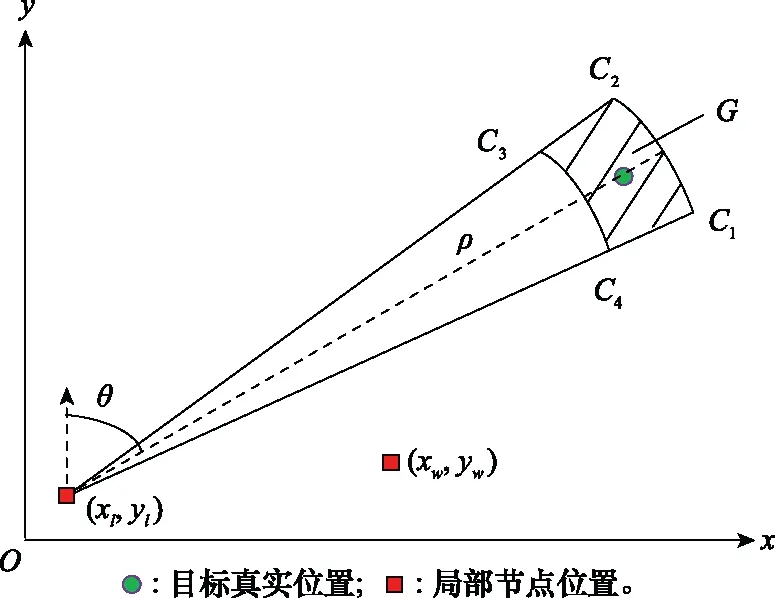
圖1 系統誤差雙側區間化示意圖Fig.1 Diagram of bilateral interval of system bias

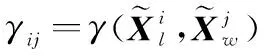
(5)

越大說明航跡和航跡越有可能對應同一目標,根據區間相似度,可利用多維分配法進行航跡關聯判定。

2.2 航跡序列相似度的計算

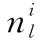
(6)

式中:

=[,,,]=[,,,]

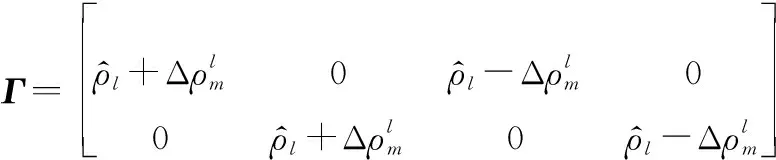
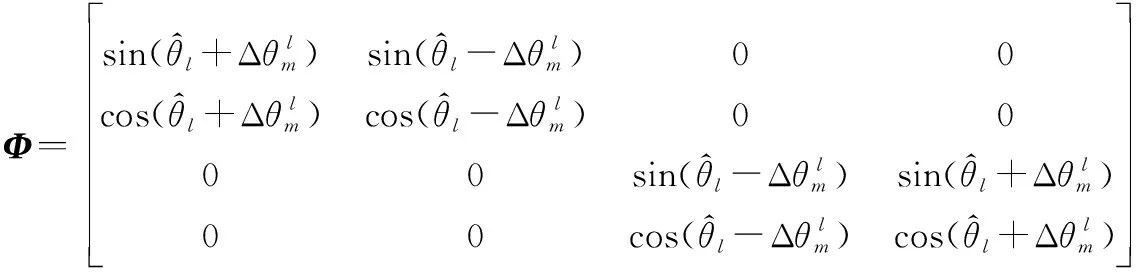
將系統誤差區間化處理后的區間坐標記為

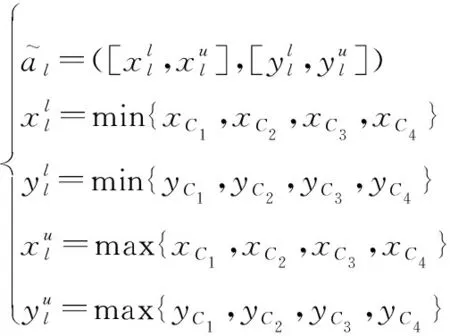
(7)

利用式(7),可將局部節點的第條航跡區間序列記為

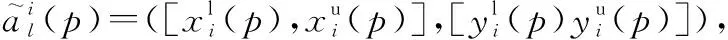
同理,可將局部節點的第條航跡區間坐標序列記為

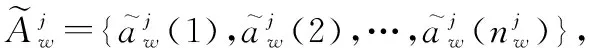
航跡區間坐標序列關聯列向量可表示為

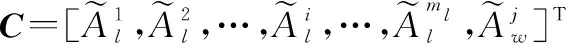
(8)

航跡區間坐標序列關聯列向量的維數為+1,每行表示各航跡區間坐標序列,由于各航跡長度不同,每行元素集合的長度也有差異。其中前行表示來自局部節點的比較航跡,第+1行表示來自局部節點的參考航跡。

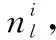
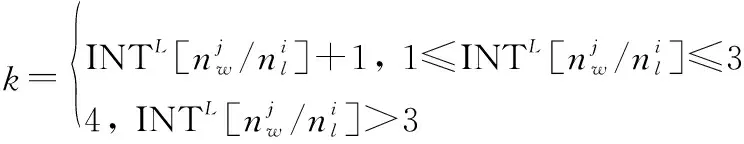
(9)

式中:INT[]表示不小于的最小整數。

根據定義1中對區間坐標序列與區間坐標點間距離的定義,計算比較序列與參考序列間的近鄰區間距離矩陣為

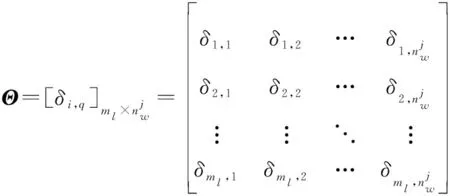
(10)

式中:

(11)

進一步利用定義2可以求得局部節點的第條航跡區間序列與局部節點的第條航跡區間序列的灰色關聯度為

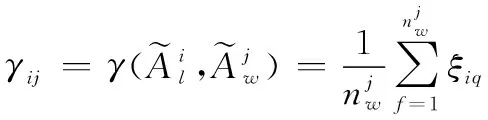
(12)

式中:

(13)

2.3 航跡關聯判決

對局部節點,上報的,條航跡一一計算灰色關聯度,組成×維灰色關聯度矩陣,利用經典分配法進行航跡關聯判決。

令變量

(14)

將目標函數記為

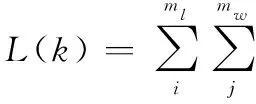
(15)

構成以下二維分配問題:

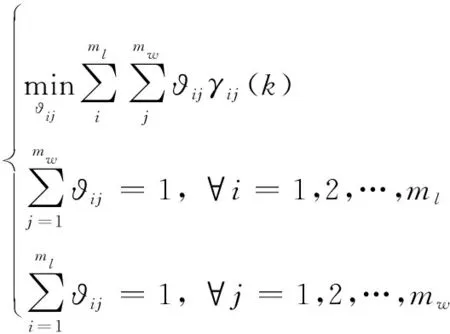
(16)

圖2給出了利用近鄰區間距離的異步抗差航跡關聯算法的流程圖。

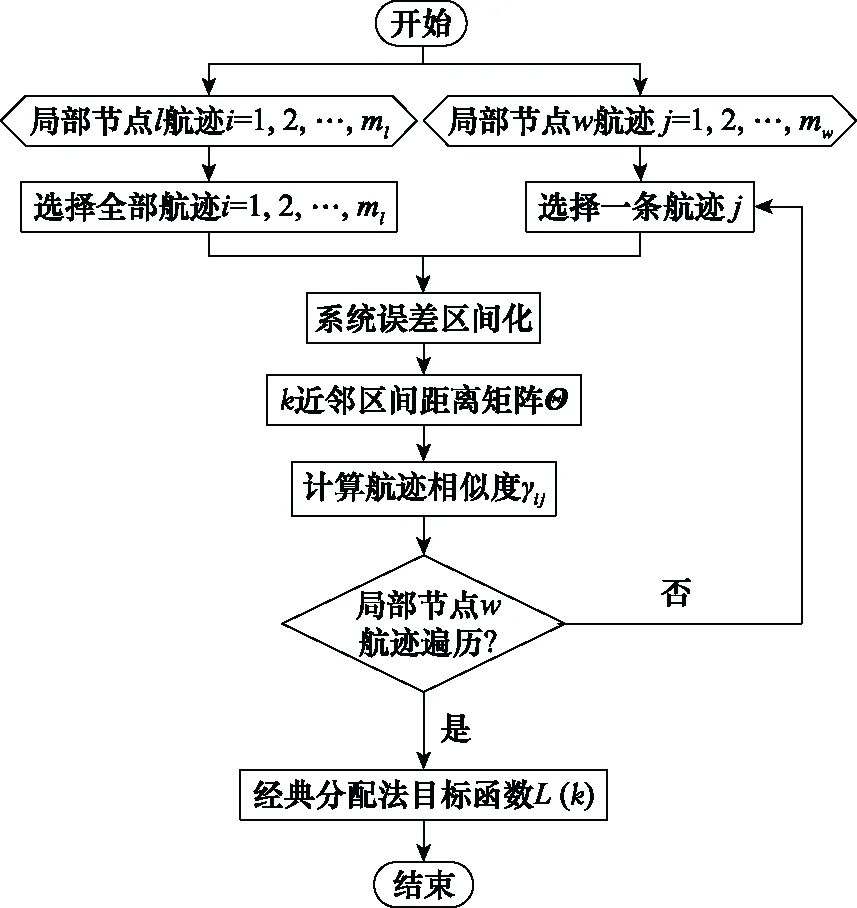
圖2 算法流程圖Fig.2 Flowchart of algorithm

3 仿真驗證與分析

3.1 仿真環境

假設多目標跟蹤系統由2個異地配置的局部節點構成,對20批目標實施不間斷跟蹤觀測35 s。局部節點1位置坐標為(0,0),局部節點2位置坐標為(100 km,0 km),局部節點1,2的傳感器采樣周期均為0.2 s。

假設機動目標在二維平面中一直處于勻速直線運動狀態,目標初始航向區間為[0,2πrad],初始航速區間為[200 m/s, 400 m/s]。局部節點1和局部節點2的傳感器測距和測角的隨機測量誤差均為=50 m、=0.02 rad。進行100次蒙特卡羅仿真實驗。

3.2 k的取值分析

對取值做出簡要理論分析:如若取值為1,相當于未對異步航跡情況做出處理,且易受個例影響導致關聯結果波動較大;若的取值等于局部節點的航跡點數目,意味著所有航跡點都將參與距離的計算,最終關聯效果將顯著降低。

圖3給出了不同取值時的耗時對比。可以看出,隨著取值增大,耗時也逐漸加大。這是因為的取值越大意味著要納入計算點跡距離的航跡區間點越多,因此耗時也越高。

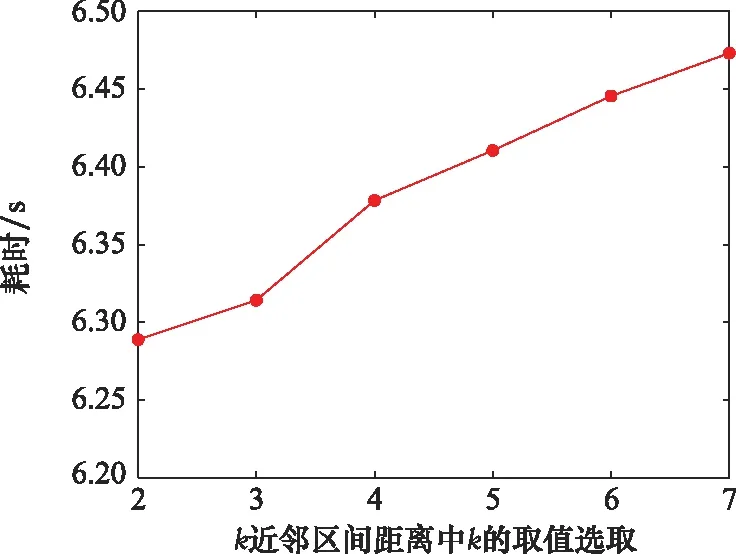
圖3 不同k取值的耗時對比Fig.3 Time comparison of different values on k

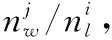
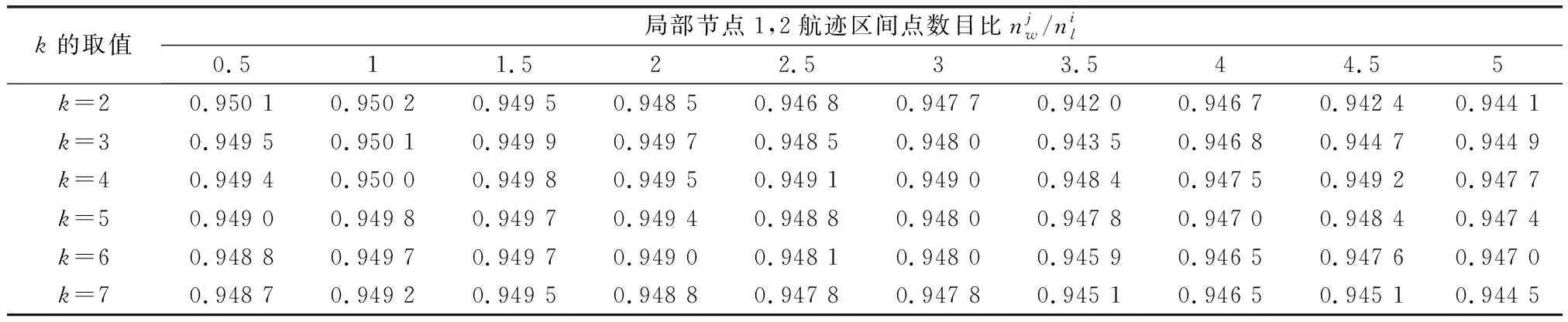
表1 不同k取值和局部節點1,2航跡區間點數目比的正確關聯率

3.3 區間化方式比較與分析

在仿真環境中,固定兩個局部節點傳感器最大測角系統誤差分別為05°和1°,假設單側區間化的測距系統誤差滿足Δ∈(0,Δ),改變兩個局部節點傳感器的最大測距系統誤差,對兩種區間化方式進行比較。

圖4給出不同區間化方式關聯結果的比較。對觀測數據的區間化處理會增加不確定度,相較于單側區間化,雙側區間化處理后數據的不確定度更大。但從圖中可知,在兩個局部節點傳感器最大測距系統誤差不同時,兩種區間化方式的關聯效果相當。由于雙側區間化對最大系統誤差的先驗信息要求低,故整體性能優于單側區間化。若在實際應用中采用雙側區間化處理,則只需知道最大系統誤差即可進行準確關聯。

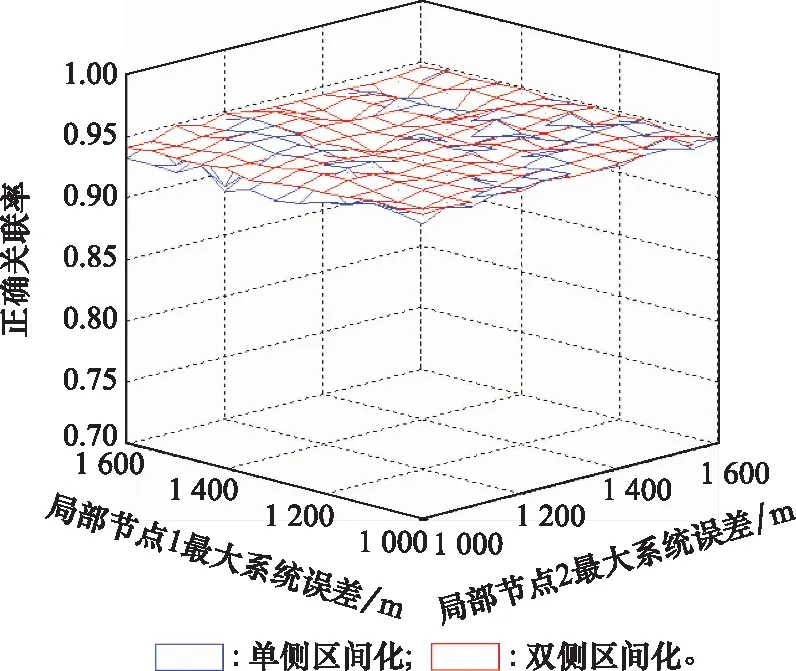
圖4 區間化方式關聯結果比較Fig.4 Comparison of correlation results of interval modes

取定一組關聯航跡數據,在不同的最大測距系統誤差下,比較近鄰區間距離相對于原始數據近鄰區間距離的增量。從圖5中可以看出,由于副對角線方向兩個局部節點傳感器的最大系統誤差差值不變,故近鄰區間距離增量保持一致。而主對角線方向系統誤差的差值對稱變化,故近鄰區間距離增量呈對稱變化。如圖4所示,雙側區間化處理后數據的不確定度較大,其近鄰區間距離增量大約是單側區間化的兩倍,但對于不同大小的系統誤差,兩種區間化方式導致的增量變化趨勢相同。在利用最小近鄰區間距離進行關聯判別時,取決于距離的相對大小而非絕對大小,故兩種區間化方式下近鄰區間距離增量的變化趨勢相同決定了其關聯效果相當。

圖5 k近鄰區間距離增量對比Fig.5 Comparison of increments of k-nearest neighbors interval dispersion

3.4 算法性能比較與分析

在仿真環境中,設置局部節點1傳感器測距和測角的最大系統誤差分別為1 000 m,1°,局部節點2傳感器取不同的最大系統誤差,比較算法的抗差性能,結果如表2所示。表中，為正確關聯率,為錯誤關聯率,為漏關聯率。選取文獻[26]算法與本文算法進行性能對比。

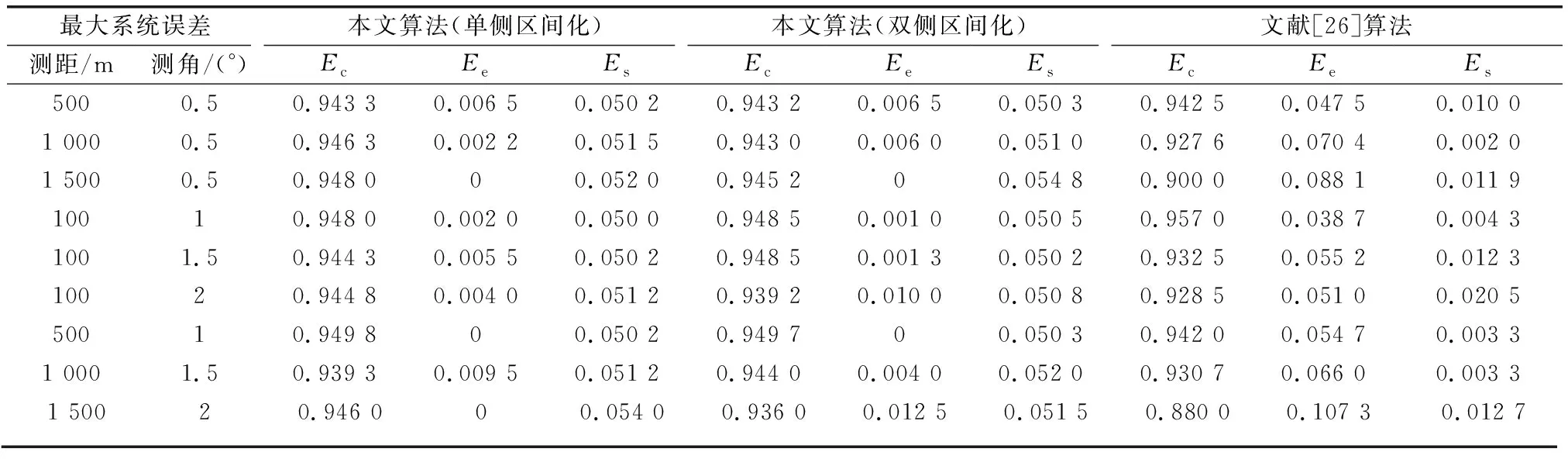
表2 不同最大系統誤差下的正確關聯率

由表2可以看出,不論是最大距離誤差還是最大角度誤差,隨著最大系統誤差的逐漸增加,文獻[26]中算法的正確關聯率有所下降,因為文獻[26]算法通過對航跡序列中兩兩對應的航跡點計算距離組成相離度矩陣進行航跡關聯判斷,系統誤差的增大會使航跡點的區間灰數范圍擴大,導致帶系統誤差的航跡距離與航跡實際距離產生較大偏差;而本文算法選取整段距離最近的個平均區間距離,具有良好的抗差性能,因此一直保持較高的正確關聯率。

另外,在判決關聯結果是否歸屬漏關聯時,本文算法通過反復試驗最終確定的漏關聯閾值門限是一個變化值,與航跡對具體關聯度有關,而文獻[26]算法采取固定值作為閾值門限,相對于變化的閾值門限更加穩定,因此本文算法的漏關聯率比文獻[26]算法高。

局部節點傳感器開始采樣時機或采樣頻率的不同易造成航跡的異步不等速率,而傳統關聯算法的假設前提中,航跡異步或系統誤差只存在其一。在仿真環境中,保持局部節點1,2傳感器測距和測角的最大系統誤差為1 000 m,1°,研究航跡異步的影響。

由于文獻[26]算法是以航跡同步為前提的抗差關聯算法,只能在所有航跡序列等長且時間戳一致情況下進行關聯,因此在實驗前先對文獻[26]算法進行時域配準預處理,使其適應航跡異步環境。

從表3中可以看出,采樣周期以及開機時機不同對文獻[26]算法的正確關聯率影響較大,這是因為對文獻[26]算法進行同步化處理會引入不必要的誤差,影響總體關聯質量;而本文算法中度量指標近鄰區間距離的求解是在航跡點與航跡序列間尋找相對較近的距離,并未利用時間信息,也不要求航跡序列等長,航跡異步并不會改變各航跡序列對的近鄰區間距離值,因此本文算法的關聯效果沒有受到影響。

表3 不同采樣頻率和開始采樣時機的正確關聯率

3.5 算法復雜度分析

以同等長度的航跡序列為前提,表4比較了文獻[26]算法和本文算法的乘法、加法運算量,表中為航跡批數,為航跡點數,為本文算法近鄰區間距離的變量。

表4 算法運算量對比

在實際運算中,乘法耗時會大于加法耗時,顯然,本文算法運算量要高于文獻[26]中算法。這是因為文獻[26]算法只解決了系統誤差下的航跡關聯問題,而本文算法可在異步和系統誤差并存情況下直接關聯,在處理異步航跡時,利用區間距離信息需要一定的計算量。另外,本文算法的單側區間化與雙側區間化只是對數據的預處理方式不同,因而單、雙側區間化的運算量相同。

圖6比較了不同航跡數目下各算法的耗時。可以看出,隨著航跡數目的增加,本文提出的兩種區間化處理方式耗時相當,但整體而言,本文算法耗時高于文獻[26]中算法,結果與表4中的理論分析吻合。

圖6 不同航跡數目下的耗時對比Fig.6 Time-consuming comparison under different track numbers

4 結 論

本文提出一種利用近鄰區間距離的異步抗差關聯算法,定義區間坐標序列與區間坐標點間的近鄰區間距離,并給出系統誤差區間化方法。對系統誤差先驗信息的要求低,具有良好的抗差性能,且算法可不做時域配準直接處理航跡異步問題。