f(R)-CIM AdS時空的相變及P-v臨界性
魏浩宸, 齊德江, 田 野, 方戈亮
(1. 沈陽工程學院 電力學院, 沈陽 110136;2. 沈陽師范大學 物理科學與技術學院, 沈陽 110034)
0 引 言
相變與臨界性是當前物理學研究的熱點前沿課題之一。f(R)-CIM AdS時空帶有引力修正參數, 會對熱力學性質產生重要影響。因而,對AdS時空的解和相關熱力學性質的進一步研究是十分有意義的。此外,AdS時空的相結構也更加豐富[1-7]。近年來,f(R)-CIM AdS度規引起了人們廣泛關注[8-12], 該度規帶有引力修正參數,因而將對熱力學性質產生重要影響,由此,研究在延伸相空間中的f(R)-CIM AdS時空的相變和臨界性是一項非常有意義的工作。
1 P-v臨界性
荷電f(R)-CIM AdS時空度規為[12]

(1)
其中

(2)
在這里,Λ與常曲率標量R0的關系為R0=4Λ,其中,Q和M代表電荷和質量。時空的熵、溫度為
在延伸相空間中,Λ被作為熱力學變量壓強:

(5)
與其共軛的量熱力學體積為

(6)
由對應的溫度與壓強的關系可以得到
P=P(V,T)
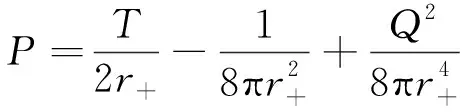
(7)
其中
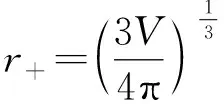
(8)
通過定義v=2r+,狀態方程(7)可改寫為

(9)
由此狀態方程(9),利用如下關系式可求得其臨界值。
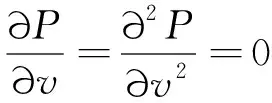
(10)
即
聯立上述2式,解得臨界體積和臨界溫度vC和TC:
將vc和TC帶入狀態方程得臨界壓強Pc為
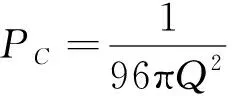
(15)
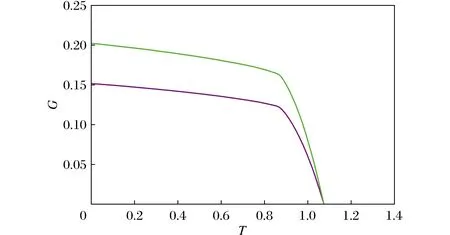
當取Q=0.05時,可計算得到臨界值分別是TC=0.500 2,vC=0.424 3,PC=1.326 3。當T (16) 上述方程的解為 圖1 P-v關系圖像Fig.1 P-v relationship curve 由狀態方程式(7)及其所求得的臨界值可繪出不同溫度下的P-v相圖,如圖1所示。該曲線從上到下依次對應的溫度分別為T=1.3>TC,T=TC=0.863 3,TC>T=0.68,T=T0=0.612 6,T0>T=0.4。最上面的曲線對應于溫度T>TC時的“理想氣體”相,第2條曲線對應于溫度等于臨界值(T=TC),最下面2條曲線對應于溫度低于臨界溫度,其中第4條曲線對應T=T0,第5條曲線對應T 在包含宇宙學常數A的擴展相空間中,吉布斯自由能為 (19) 圖2 當P=PC=1.326 3時的G-T圖像Fig.2 G-Trelationship curve when P=PC=1.326 3 結合方程(4)和方程(19),并且利用如下關系 (20) 可得 由方程(22),可得 (23) 將關系式v=2r+代入方程(23),推導得到 聯立以下2個方程 可畫出不同壓強下的吉布斯自由能與溫度的G-T圖像,如圖2(Q=0.05,ζ的取值由上到下依次為ζ=4和ζ=3)、圖3(Q=0.1,ζ的取值由上到下依次為ζ=4和ζ=3)和圖4(Q=0.05,ζ的取值由上到下依次為ζ=4和ζ=3)所示。在這里,取Q=0.05,臨界壓強PC=1.326 3。 圖3 當P 圖4 當P=2>PC時的G-T圖Fig.4 G-Trelationship curve when P=2>PC 如圖2、圖3和圖4所示,當p=pc時,G-T圖像出現了一個拐點,表明時空存在二階相變;當p 本文選擇(P-v)作為狀態參數,運用其物態方程計算了相關臨界值,并繪出了P-v相圖,由此研究了f(R)理論中荷電f(R)-CIM AdS時空的臨界行為和相變結構。并且本文繪出了不同狀態下的G-T圖像,以此了解f(R)-CIM AdS時空的相變及局部和整體穩定性。此外,還考慮了f(R)參數ζ對相變的影響。結果表明荷電f(R)-CIM AdS時空存在類似于普通熱力學氣-液流體系統的范德瓦爾斯相變。 致謝感謝沈陽工程學院大學生創新創業項目(202011632084)的支持。

2 G -T圖像
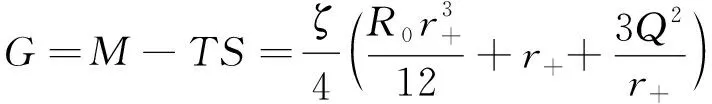




3 結 論

