基于瞬時相位的微地震干涉定位方法研究

戰(zhàn)婷婷， 李磊， 陳浩

1 中國科學(xué)院聲學(xué)研究所聲場聲信息國家重點實驗室， 北京 100190 2 中國科學(xué)院大學(xué)， 北京 100049 3 北京市海洋深部鉆探測量工程技術(shù)研究中心， 北京 100190 4 中南大學(xué)地球科學(xué)與信息物理學(xué)院， 長沙 410083 5 有色金屬成礦預(yù)測與地質(zhì)環(huán)境監(jiān)測教育部重點實驗室(中南大學(xué))， 長沙 410083

0 引言

微地震監(jiān)測技術(shù)是利用地下應(yīng)力場變化導(dǎo)致巖層破裂而誘發(fā)的微弱地震波進行儲層監(jiān)測和描述的地球物理方法(Maxwell, 2014; Li et al., 2019; 李政等，2019).該方法是根據(jù)震源位置的分布對裂縫形態(tài)或儲層流體運動進行監(jiān)測，因此震源定位是微地震數(shù)據(jù)處理和解釋的基礎(chǔ).研究者們借鑒反射地震勘探中偏移疊加的思想，提出了一些無需初至拾取、利用多道波形信息的自動震源定位方法(Kao and Shan, 2004; 許力生等，2013；李振春等，2014；Cesca and Grigoli, 2015; Li et al., 2020).這類方法中研究最成熟且應(yīng)用最廣的是波形疊加法.波形疊加法的核心思想是采用不同的偏移核函數(shù)進行波束形成，即挖掘走時和幅度之間的對應(yīng)關(guān)系對地震震源能量進行聚焦和成像，從而實現(xiàn)震源定位(Gajewski et al., 2007; 王維波等，2012；曹雷，2015；Li et al., 2018).

地震干涉成像是一種具有代表性的偏移疊加類震源定位法.該方法基于震源到不同檢波器的走時差，消除了震源激發(fā)時刻對定位精度的影響.由于采用走時差信息提取對應(yīng)的互相關(guān)波形進行疊加，該方法也被稱作互相關(guān)疊加或互相關(guān)偏移(Li et al., 2018).Schuster等(2004)首次提出地震干涉法可以對被動地震數(shù)據(jù)進行震源定位.Li等(2015)提出了加權(quán)彈性波干涉成像，該方法通過考慮不同震相的加權(quán)組合，提高了定位結(jié)果的可靠性.Poiata等(2016)提出基于多頻段的互相關(guān)疊加震源定位法，并將其成功應(yīng)用于智利中部地區(qū)的地震檢測和定位.Wu等(2018)通過將反褶積干涉與互相關(guān)偏移結(jié)合，提出了微地震定位的反褶積偏移方法，合成算例和實際算例均表明新方法能大幅提高成像分辨率，并降低了對速度模型誤差的敏感性.田宵等(2020)在加權(quán)彈性波干涉成像的基礎(chǔ)上提出了增加同一檢波器的S-P波走時差信息的全干涉成像方法，能夠顯著降低震源-檢波器方向的定位誤差和偽像.由于微地震事件一般具有復(fù)雜的震源機制，為了消除震源輻射花樣導(dǎo)致的初至極性變化的影響，避免出現(xiàn)波形相消疊加的問題，一般需要采用特征函數(shù)對原始波形進行轉(zhuǎn)換.目前主要的特征函數(shù)有絕對值(Kao and Shan, 2004)、波形包絡(luò)(Gharti et al., 2010)、振幅的平方(Gajewski et al., 2007)和長短時窗能量比(Short Time Average to Long Time Average ratio, STA/LTA)(Grigoli et al., 2013)等.Trojanowski和Eisner(2016)從數(shù)值和理論分析兩方面表明，絕對值等特征函數(shù)會降低波形疊加的噪聲壓制性能，對波形極性簡單的校正就能顯著提高事件檢測和定位效果，而與波形相似性/互相關(guān)疊加定位方法相結(jié)合可以獲得更好的定位結(jié)果.Beskardes等(2018)對比了基于原始波形、波形包絡(luò)、長短時窗能量比(STA/LTA)和峰度(Kurtosis)四種特征函數(shù)的微地震定位方法，結(jié)果表明：一方面原始波形能夠提供最佳的空間分辨率，保留幅度信息并增強了檢測微弱事件的能力，但對速度誤差、極性誤差和突發(fā)噪聲最為敏感；另一方面其他特征函數(shù)能有效避免初至極性的影響并降低對速度誤差的敏感性，但犧牲了成像的空間分辨率并且容易受噪聲影響.震源定位和震源機制聯(lián)合反演法是一種消除初至極性變化影響的替代方案，但是這種方法反演速度較慢，對數(shù)據(jù)質(zhì)量要求較高，并且還可能會將震源機制反演過程中的誤差引入定位結(jié)果中(Staněk et al., 2015).

除了幅度信息，相位信息也能體現(xiàn)波形極性.Schimmel和Paulssen(1997)提出了一種基于瞬時相位相干度量的相位加權(quán)疊加法(Phase-Weighted Stack, PWS).王曉欣等(2017)將PWS方法用于天然地震事件的定位中，通過理論地震圖計算驗證了方法的可靠性.Tan(2019)詳細(xì)驗證了PWS相對于其他方法的優(yōu)越性，發(fā)現(xiàn)PWS具有更好的空間分辨率，提高了微弱地震事件的可檢測性.

本文從原始互相關(guān)波形出發(fā)，將包含波形極性信息的相位屬性引入干涉成像法中，通過重新組合原始互相關(guān)波形的振幅和瞬時相位信息，提出了一種同時基于振幅和瞬時相位信息的干涉成像方法——互相關(guān)相位加權(quán)成像法(Cross-Correlation Phase-Weighted imaging method, CCPW)，實現(xiàn)校正波形極性以及提高抗噪性和成像分辨率的目的.然后，與基于絕對值干涉成像法(Absolute value-based Interferometric Imaging method, AII)和基于STA/LTA干涉成像法(STA/LTA-based Interferometric Imaging method, SLII)一起，采用地面監(jiān)測的水平分層理論模型分析了隨機噪聲、分辨率、速度模型誤差和震相數(shù)量等因素對定位結(jié)果的影響.最后將三種方法應(yīng)用到礦震地面監(jiān)測的現(xiàn)場數(shù)據(jù)中，結(jié)果表明，提出的定位方法具有較強的抗噪性并提高了成像分辨率，但定位結(jié)果受高幅值S波等的相干干擾，并且對速度模型的誤差敏感.

1 基本原理

1.1 微地震干涉成像

微地震干涉成像的基本原理：建立速度模型并離散化，通過射線追蹤或求解程函方程計算得到檢波器到速度模型中各離散點的直達(dá)波走時表，提取震源到獨立檢波器對的走時差并對相應(yīng)的互相關(guān)波形進行偏移疊加，疊加所有檢波器對的成像結(jié)果生成最終震源成像剖面(Schuster et al., 2004; Li et al., 2015).對應(yīng)的干涉成像方程如下：

(1)

(2)

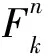
1.2 互相關(guān)相位加權(quán)成像法

對地震信號s(t)做希爾伯特變換H[s(t)]，并構(gòu)建解析信號sa(t)如下：

sa(t)=s(t)+iH[s(t)]=A(t)exp[iφ(t)],

(3)

(4)

式中，A(t)和φ(t)為隨時間變化的包絡(luò)和瞬時相位.

對逐采樣點歸一化的解析信號exp[iφ(t)]進行疊加并歸一化，可以得到相位疊加(Phase Stack, PS)w(t)：

(5)

(6)

式中，φl(t)為第l道的瞬時相位，v為控制最終相位疊加曲線w(t)尖銳程度的指數(shù)，也能夠控制隨機噪聲經(jīng)過疊加后的衰減程度.式(6)表明只有相位一致的有效信號才能得到相干疊加，其他相位隨機變化的噪聲信號經(jīng)過疊加只能得到一個小值(Schimmel and Paulssen, 1997).

為了抑制不相干的疊加信號，將相位疊加作為線性疊加的時間相關(guān)的權(quán)重，得到相位加權(quán)疊加(PWS)gPWS(t)：

(7)

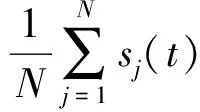
而微地震事件具有復(fù)雜的震源機制，將式(7)直接用于微地震事件的定位時(王曉欣等，2017；Tan, 2019)，未考慮具有不同極性的波形對定位結(jié)果的影響.于是，為了校正波形極性對定位結(jié)果的影響，考慮重新組合振幅和瞬時相位屬性信息，并應(yīng)用于干涉成像方法中.

(8)

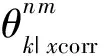
從表1的推導(dǎo)可以發(fā)現(xiàn)，無論波形的振幅極性為正或為負(fù)，通過新方法的處理，最后加權(quán)乘積的結(jié)果均變換為波形的振幅極性為正時的乘積形式，也就是說波形的極性得到了校正.

表1 互相關(guān)相位加權(quán)成像法極性校正原理Table 1 Polarity correlation principle of CCPW

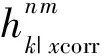
(9)

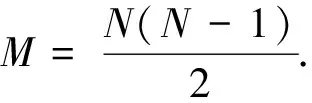
2 數(shù)值模擬

2.1 均勻模型下的方法驗證

首先，通過簡單的二維均勻介質(zhì)模型驗證方法的有效性，采用地面陣列監(jiān)測，震源為加載在正應(yīng)力分量上的爆炸震源，震源函數(shù)為雷克子波函數(shù)，其他相應(yīng)參數(shù)見表2.

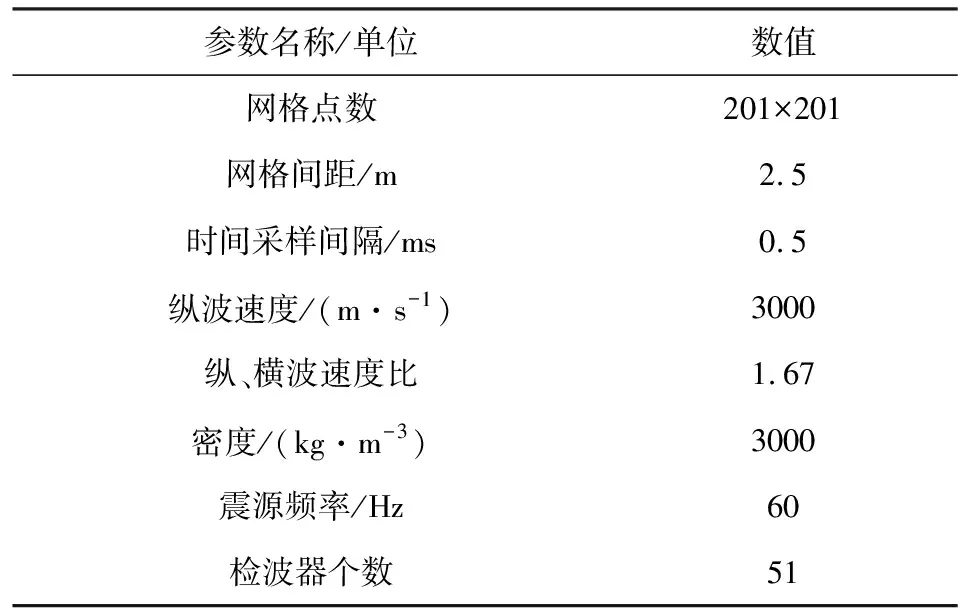
表2 二維均勻模型參數(shù)Table 2 Parameters of two-dimensional homogeneous model

地面51道檢波器接收到的波形如圖1所示.由圖可見，在均勻速度模型中爆炸源只激發(fā)P波，Vx分量接收到的波形關(guān)于震源位置的橫坐標(biāo)有明顯的初至極性變化，而Vz分量接收到的波形極性一致.

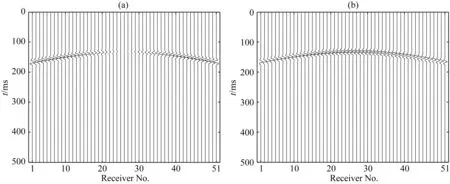
圖1 合成微地震記錄 (a) Vx分量; (b) Vz分量.Fig.1 Synthetic microseismic records (a) Vx component; (b) Vz component.

以Vx分量的第1道與第13道的原始互相關(guān)波形和第1道與第38道的原始互相關(guān)波形為例，說明互相關(guān)相位加權(quán)成像法是如何校正波形極性的.圖2(a,b)分別為上述兩道波形極性相反的原始互相關(guān)波形，圖2(c,d)分別為由式(5)得到的這兩道原始互相關(guān)波形對應(yīng)的逐采樣點歸一化的解析信號，圖2(e,f)分別為由式(8)得到的兩道原始互相關(guān)波形與其對應(yīng)的逐采樣點歸一化的解析信號的加權(quán)乘積，其中六角星代表參考點，圖2c中已示出各象限位置，且圖2(d—f)中的象限位置與其一致，圖中水平和垂直的黑色實線分別表示實軸和虛軸的位置.在由實軸為橫軸和虛軸為縱軸構(gòu)成的復(fù)數(shù)平面中，逐采樣點歸一化的解析信號中點的實部的極性決定該點落在虛軸右側(cè)還是左側(cè)，即當(dāng)實部極性為正時，該點落在虛軸的右側(cè)，也就是第一和第四象限，反之當(dāng)實部極性為負(fù)時，該點落在虛軸左側(cè)也就是第二和第三象限.由式(3)中解析信號的實部為原始互相關(guān)波形可知，此時式(5)中經(jīng)過逐采樣點歸一化的解析信號中只包含相位信息且點的實部的極性與原始互相關(guān)波形中點的極性一致，也就是說由于圖2c、d中兩個逐采樣點歸一化解析信號中的點在虛軸左右兩側(cè)均存在，且兩個原始互相關(guān)波形中對應(yīng)顏色的參考點此時恰好分布在大約關(guān)于原點對稱的位置上，表明兩個原始互相關(guān)波形的極性相反，而圖2e、f中加權(quán)乘積后信號中對應(yīng)顏色的參考點則分別以近似相同的相位落在了虛軸右側(cè)的第一和第四象限中距離原點與振幅大小相等的位置上，說明經(jīng)過變換后的波形極性得到了校正.

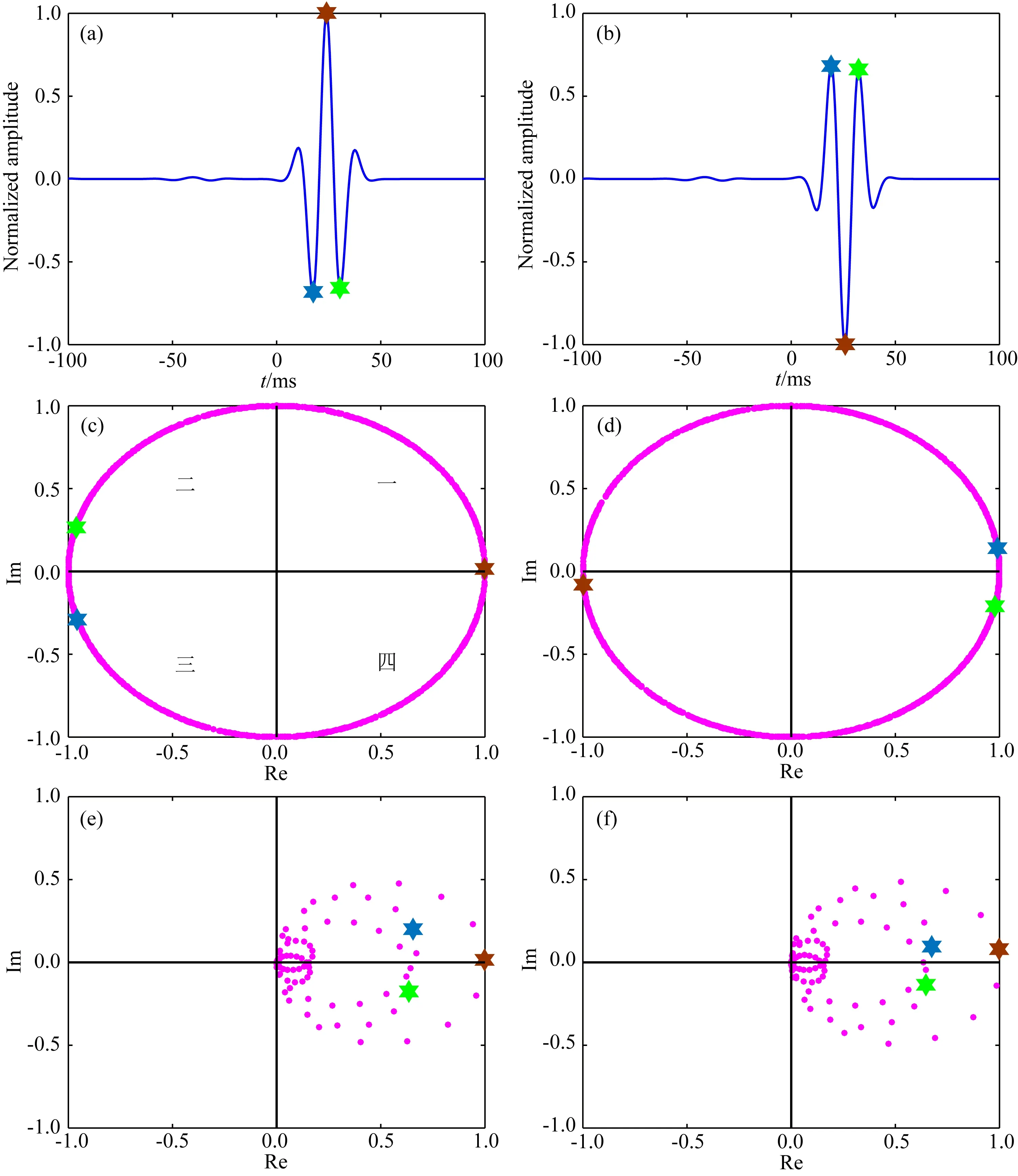
圖2 互相關(guān)相位加權(quán)成像法的極性校正原理示意圖 (a,b) 第1道分別與第13道、第38道的原始互相關(guān)波形； (c,d) 原始互相關(guān)波形(a)和(b)對應(yīng)的逐采樣點歸一化的解析信號； (e,f) 原始互相關(guān)波形與對應(yīng)的逐采樣點歸一化的解析信號的加權(quán)乘積.Fig.2 Sketch of polarity correction principle of CCPW (a,b) The original cross-correlation waveforms of the 1st trace and the 13th trace, the 38th trace, respectively; (c,d) The analytical signals normalized sample by sample corresponding to the original cross-correlation waveforms (a) and (b); (e,f) The weighted products of the original cross-correlation waveforms and the corresponding analytical signals normalized sample by sample.

v的作用可由圖3說明，從式(9)可知，v是針對歸一化后的疊加值操作的，此時的疊加值大小在[0,1]范圍內(nèi).從圖3中不同v的取值對應(yīng)的疊加值變化曲線可以看出：將疊加值取指數(shù)v后，不同疊加值的衰減程度不同，相同v的取值下，由隨機噪聲引起的低疊加值衰減程度明顯大于由有效信號引起的高疊加值，凸顯了震源能量，最終的成像分辨率得到提高；同時，當(dāng)v的取值在[2,5]內(nèi)時，對低疊加值的衰減效果已經(jīng)十分有效，且隨著指數(shù)v的取值越大，越抑制高疊加值，對低疊加值的衰減效果則變化不大.故本文的v值在該范圍內(nèi)選取，以防止過高的v的取值導(dǎo)致定位結(jié)果出現(xiàn)不穩(wěn)定性問題.

現(xiàn)在，Vx分量的獨立且不重復(fù)的原始互相關(guān)波形經(jīng)過線性偏移疊加和經(jīng)過互相關(guān)相位加權(quán)成像法偏移疊加后的波形對比如圖4a所示，可以發(fā)現(xiàn)：有正負(fù)極性變化的原始互相關(guān)波形經(jīng)過線性偏移疊加后相互抵消，無法得到有效的能量峰值；而經(jīng)過互相關(guān)相位加權(quán)成像法得到的疊加波形中存在有效的高能量峰值，說明原始互相關(guān)波形的極性得到了校正；通過控制v的取值可以削弱旁瓣，并且隨著v的取值增大，疊加波形的旁瓣被衰減的越明顯.

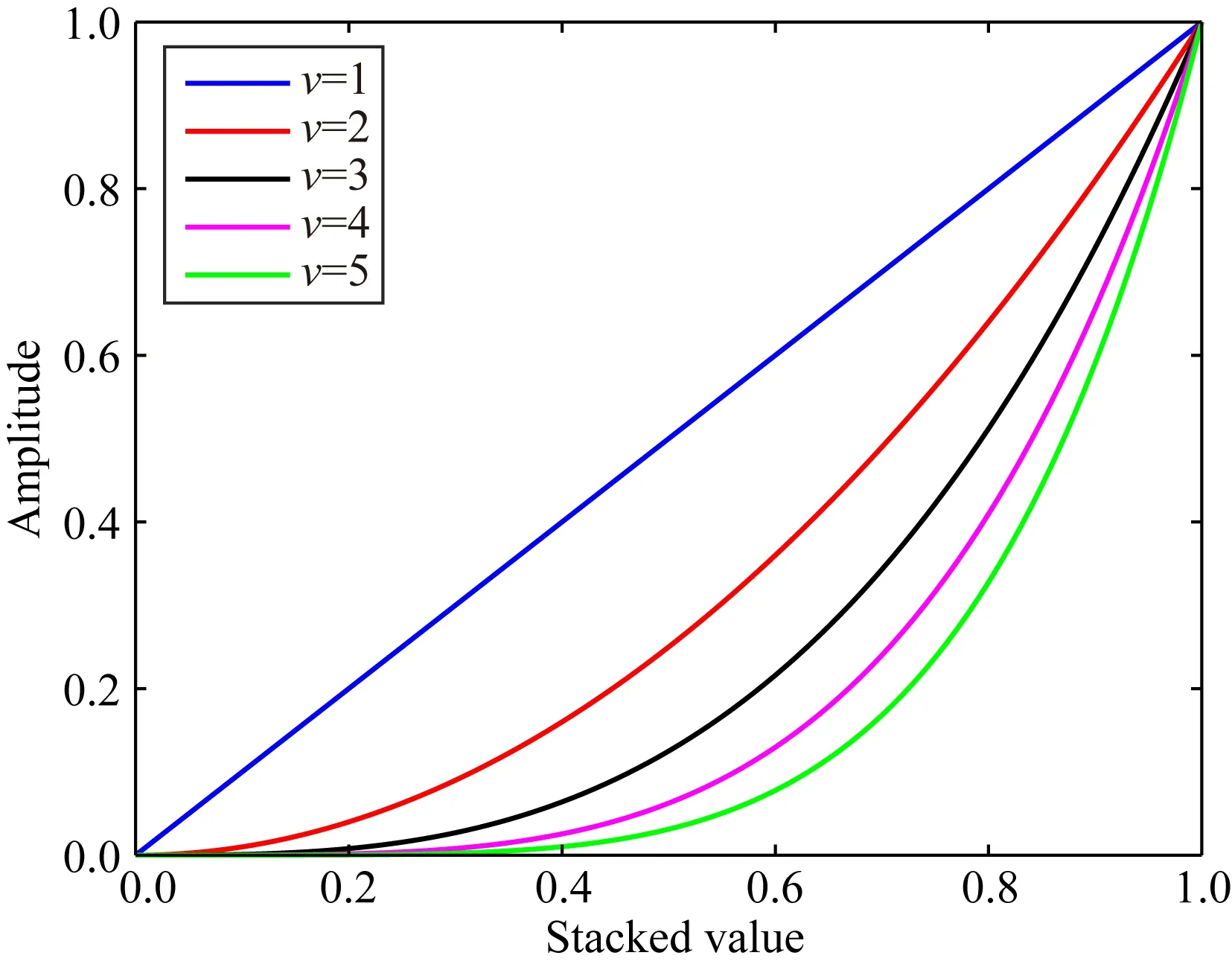
圖3 最終疊加值隨指數(shù)v的取值變化示意圖Fig.3 Sketch of the final stacked value changing with the value of exponent v

為了說明互相關(guān)相位加權(quán)成像法與基于絕對值干涉成像法的區(qū)別，向Vx分量的每道原始波形中分別添加了所有道波形最高振幅的均方差40%的高斯隨機噪聲，獨立且不重復(fù)的原始互相關(guān)波形經(jīng)過二者處理后得到的疊加波形如圖4b所示：當(dāng)v=1時，互相關(guān)相位加權(quán)成像法和基于絕對值干涉成像法的疊加結(jié)果類似；由于互相關(guān)相位加權(quán)成像法中引入了相位信息，瞬時相位隨機變化的噪聲信號在疊加過程中得到了有效的衰減，提高了方法的抗噪性；與壓制旁瓣一樣，隨機噪聲也可以通過調(diào)整v的取值進一步削弱，提高最終成像分辨率.也就是說，由于互相關(guān)相位加權(quán)成像法的疊加結(jié)果受振幅和瞬時相位共同影響，相比在時域中簡單疊加波形幅度的基于絕對值干涉成像法具有更好的抗噪性和成像分辨率.

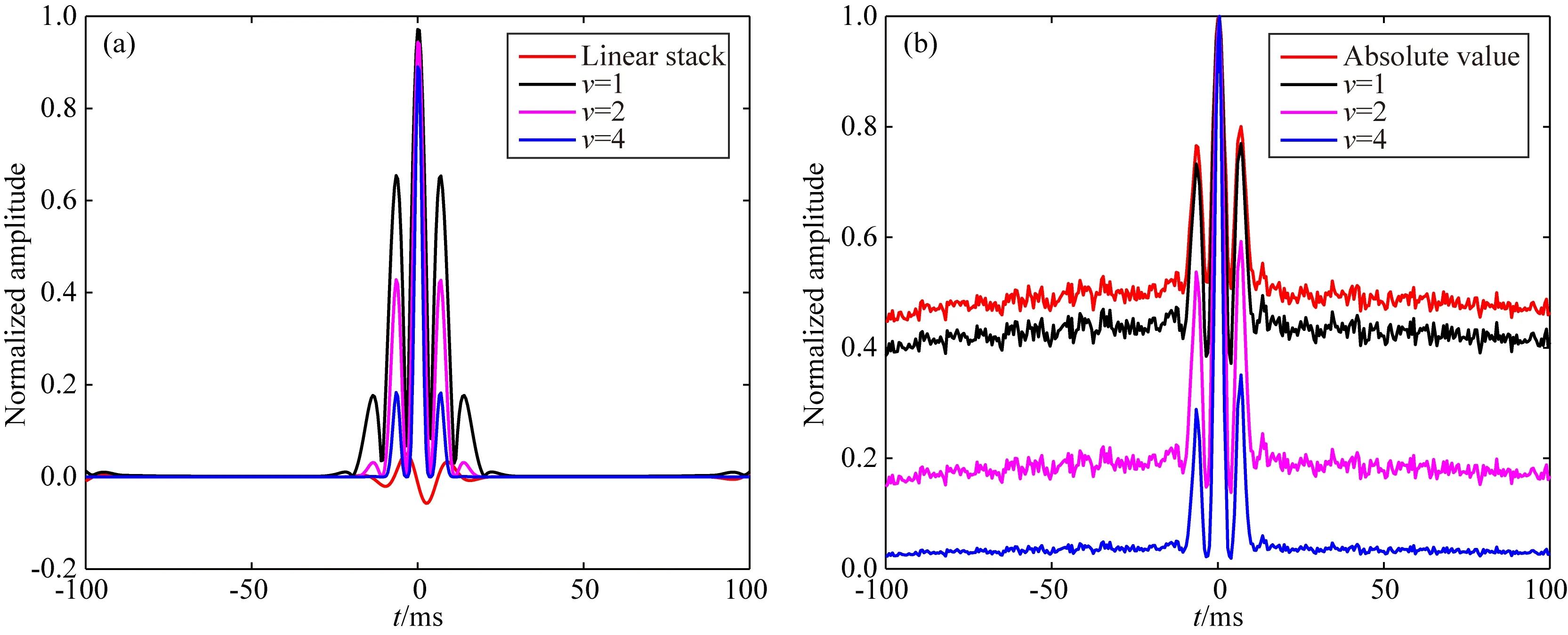
圖4 互相關(guān)波形偏移疊加結(jié)果對比 (a) 無噪Vx分量，所有獨立的原始互相關(guān)波形經(jīng)過線性偏移疊加和互相關(guān)相位加權(quán)成像法偏移疊加得到的波形(v的取值分別為1，2，4)； (b) 含噪Vx分量，所有獨立的原始互相關(guān)波形經(jīng)過取絕對值后線性偏移疊加和互相關(guān)相位加權(quán)成像法偏移疊加得到 的波形(v的取值分別為1，2，4).Fig.4 Comparison of cross-correlation waveforms migration stacking results (a) Vx component without noise, the waveforms obtained by linear migration stacking and CCPW migration stacking (the values of v are 1, 2, 4, respectively) of all independent and original cross-correlation waveforms; (b) Vx component with noise, the waveforms obtained by linear migration stacking after taking absolute value and CCPW migration stacking (the values of v are 1, 2, 4, respectively) of all independent and original cross-correlation waveforms.

基于原始波形干涉成像法、互相關(guān)相位加權(quán)成像法、基于絕對值干涉成像法和基于STA/LTA干涉成像法對無噪Vx分量成像結(jié)果的對比如圖5所示，能夠發(fā)現(xiàn)互相關(guān)相位加權(quán)成像法不僅校正了波形極性變化對定位結(jié)果的影響，還明顯地提高了最終的成像分辨率.

2.2 分層模型下的方法性能對比測試

為了進一步驗證互相關(guān)相位加權(quán)成像法的穩(wěn)定性和可靠性，基于二維水平分層各向同性介質(zhì)模型進行了系列數(shù)值試驗.速度模型及震源-檢波器陣列示意圖如圖6a所示，圖中三層水平分層模型參數(shù)如下：由上到下的層密度依次為2000 kg·m-3、2500 kg·m-3和3000 kg·m-3，層縱波速度依次為2000 m·s-1、2500 m·s-1和3000 m·s-1，縱橫波速度比均為1.67.為不失一般性，在不同位置設(shè)置四個震源S1、S2、S3和S4，相應(yīng)的位置信息已在圖中示出，并獨立激發(fā)分別對應(yīng)研究了隨機噪聲、分辨率、速度模型誤差和震相數(shù)量等因素對各種方法定位結(jié)果的影響.其中，互相關(guān)相位加權(quán)成像法中v的取值為2， STA/LTA方法中短時窗的長度為7.5 ms，長時窗長度為15 ms.所有震源均是水平激發(fā)的集中力源，其他參數(shù)與上述均勻介質(zhì)模型參數(shù)一致.圖6b、c分別為向震源S1的每道原始波形中添加所有道波形最高振幅的均方差50%的高斯隨機噪聲后的Vx分量和Vz分量.

2.2.1 隨機噪聲

首先向震源S1的各道原始波形中分別添加所有道波形最高振幅的均方差20%、30%、40%和50%的高斯隨機噪聲，并采用蒙特卡洛方法研究定位的不確定性(Maxwell, 2009; Tian et al., 2016,2017)，其主要做法是對每種噪聲水平，預(yù)先生成100組隨機噪聲并添加在原始波形上，進行100次定位，最后根據(jù)100次定位結(jié)果分析其分布特征和穩(wěn)定性(魯棒性).三種方法在各噪聲水平下100次蒙特卡洛模擬的定位結(jié)果如圖7所示，結(jié)果表明：所有方法的定位誤差主要集中在垂直方向(Z)，這是由于干涉成像法的二維成像剖面是由雙曲狀條紋疊加構(gòu)成的，導(dǎo)致在地面監(jiān)測條件下對垂直方向(Z)的約束較差，但在復(fù)雜速度模型下水平方向也會出現(xiàn)較大定位誤差；抗噪性效果最好的是互相關(guān)相位加權(quán)成像法，其次是基于絕對值干涉成像法，最差的是基于STA/LTA干涉成像法；尤其當(dāng)信噪比較低時(40%～50%)，新方法包含相位信息的偏移疊加方式相比基于絕對值干涉成像法的偏移疊加方式的優(yōu)勢逐漸體現(xiàn)出來，較大程度上降低了隨機噪聲對定位結(jié)果的影響；而STA/LTA方法的震相識別精度受隨機噪聲影響大，進而影響了最終定位結(jié)果的準(zhǔn)確性.

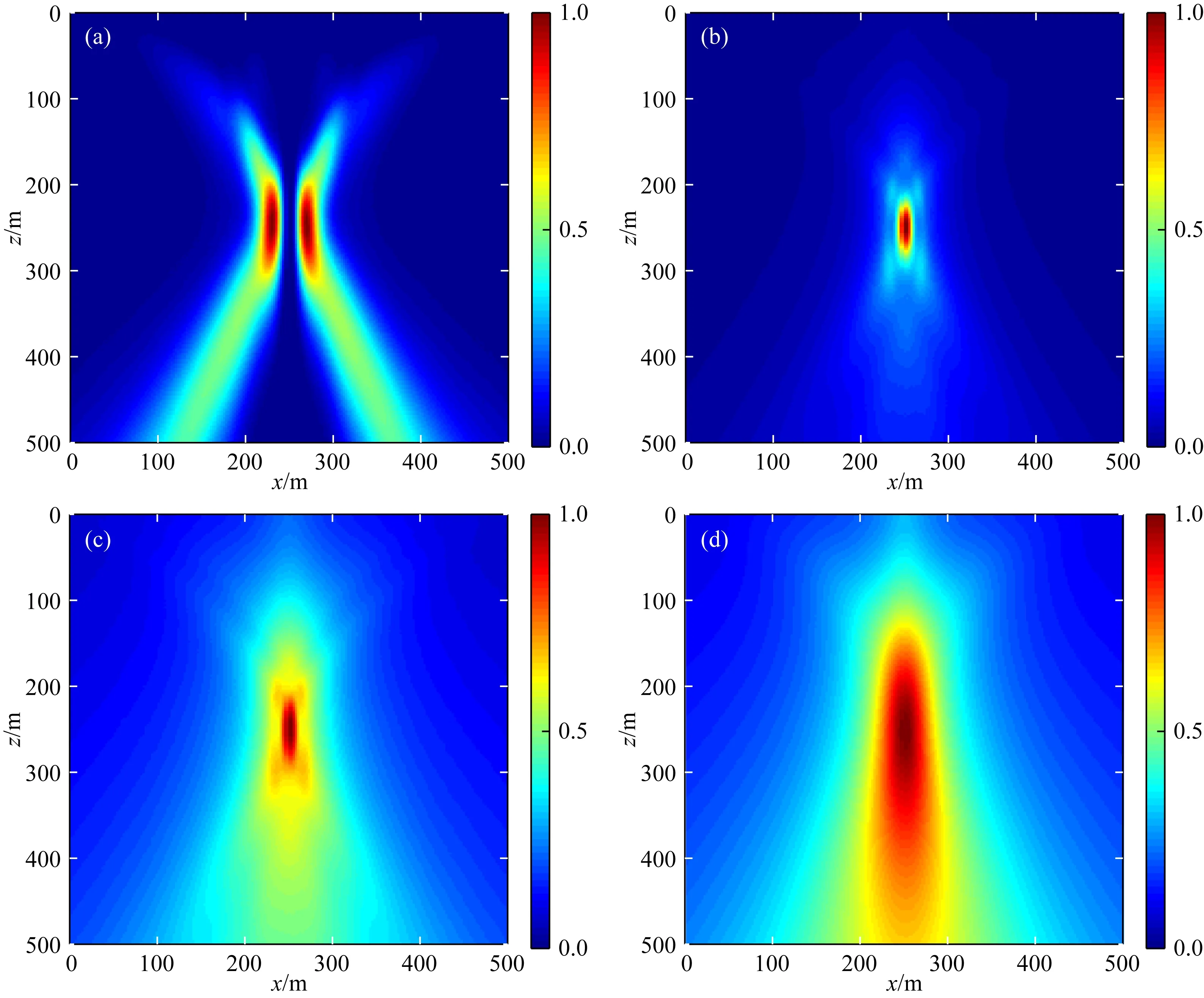
圖5 無噪聲Vx分量的干涉成像結(jié)果 (a) 基于原始波形干涉成像法； (b) 互相關(guān)相位加權(quán)成像法(v=2)； (c) 基于絕對值干涉成像法； (d) 基于長短時窗能量比干涉成像法.Fig.5 Interferometric imaging results of the Vx component without noise (a) The original waveform-based interferometric imaging; (b) CCPW (v=2); (c) AII; (d) SLII.

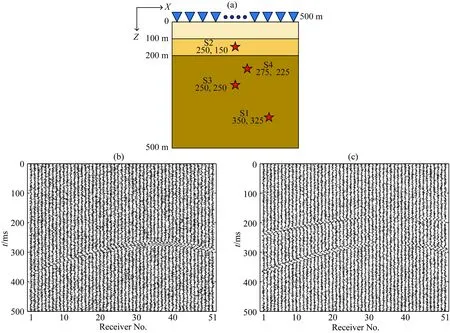
圖6 (a)速度模型和震源-檢波器陣列示意圖；震源S1添加噪聲后的(b)Vx分量波形和(c)Vz分量波形Fig.6 (a) Sketch of velocity model and source-receiver array; (b) Vx component waveforms and (c) Vz component waveforms of S1 with noise

2.2.2 分辨率

向震源S2的各道原始波形中添加了所有道波形最高振幅的均方差30%的高斯隨機噪聲，測試三種方法在低信噪比條件下的成像分辨率.已知波形的絕對頻寬影響分辨率，頻寬越大，波形“越瘦”，分辨率越高.根據(jù)該特性來確定震源成像的空間分辨率：利用成像剖面中過震源位置的歸一化成像值曲線的最高幅值的0.707倍對應(yīng)的橫坐標(biāo)寬度表示成像分辨率，此時橫坐標(biāo)寬度“越小”代表成像值曲線“越瘦”，成像分辨率越高.通過這種量化的成像分辨率定義方式能夠直觀的比較各震源成像結(jié)果的分辨率大小.三種方法的成像剖面中過震源位置的水平方向(X)和垂直方向(Z)的成像值曲線對比如圖8所示，幅值0.707對應(yīng)圖中黑色點線，可以看出：無論是水平方向(X)還是垂直方向(Z)，由黑色點線截取的成像值曲線寬度由小到大依次為：互相關(guān)相位加權(quán)成像法、基于絕對值干涉成像法和基于STA/LTA干涉成像法，即對應(yīng)著成像分辨率逐漸降低.該測試結(jié)果進一步說明了STA/LTA方法受隨機噪聲影響大，當(dāng)波形中隨機噪聲含量增大時，震相識別后的波形分辨率降低，進而導(dǎo)致最終成像分辨率變差.互相關(guān)相位加權(quán)成像法則通過包含瞬時相位信息的多道波形偏移疊加和指數(shù)v的適當(dāng)取值顯著地提高了最終成像分辨率.

2.2.3 速度模型誤差

在實際微地震定位過程中，速度模型總會存在一定的誤差，導(dǎo)致定位結(jié)果的不準(zhǔn)確.為考察三種方法對速度模型的依賴性，在各層的P、S波速度模型中分別添加±20%、±15%和±10%的速度誤差，共得到六種速度模型.以震源S3產(chǎn)生的理論波形為例，為了排除其他因素干擾，此時原始波形中不添加隨機噪聲.三種方法在六種速度模型下的定位結(jié)果與正確震源位置之間的絕對誤差如表3所示，定位結(jié)果對比如圖9所示.當(dāng)速度模型存在誤差時，所有方法的定位結(jié)果均相對正確震源位置發(fā)生了偏移，且這種偏移只發(fā)生在垂直方向(Z)上.這是因為檢波器陣列布設(shè)于地面且關(guān)于震源位置的橫坐標(biāo)對稱分布，震源水平方向(X)的定位誤差由于走時誤差的對稱約束而抵消了，而在復(fù)雜模型中，特別是存在橫向速度變化的時候水平方向也會出現(xiàn)定位誤差.當(dāng)速度模型值減小時，定位結(jié)果越遠(yuǎn)離檢波器陣列，且此時的定位誤差要大于速度模型值增大時的定位誤差.因為當(dāng)速度值減小時，模型中各離散點到檢波器對的理論計算走時差增大，只有更加遠(yuǎn)離檢波器陣列的離散點能吻合實際的互相關(guān)波形.相反，當(dāng)速度模型值增大時，震源被定位到更加靠近檢波器陣列的錯誤位置.此外，添加速度誤差的絕對值相同的條件下，速度模型減小(-20%)比速度模型增大(+20%)造成的走時差誤差更大，導(dǎo)致了速度值減小時的定位誤差更大.分辨率較高的互相關(guān)相位加權(quán)成像法和基于絕對值干涉成像法的定位誤差整體上要大于分辨率較低的基于STA/LTA干涉成像法的定位誤差.這是因為波形分辨率越高，對速度模型的誤差越敏感，定位結(jié)果的誤差也越大.

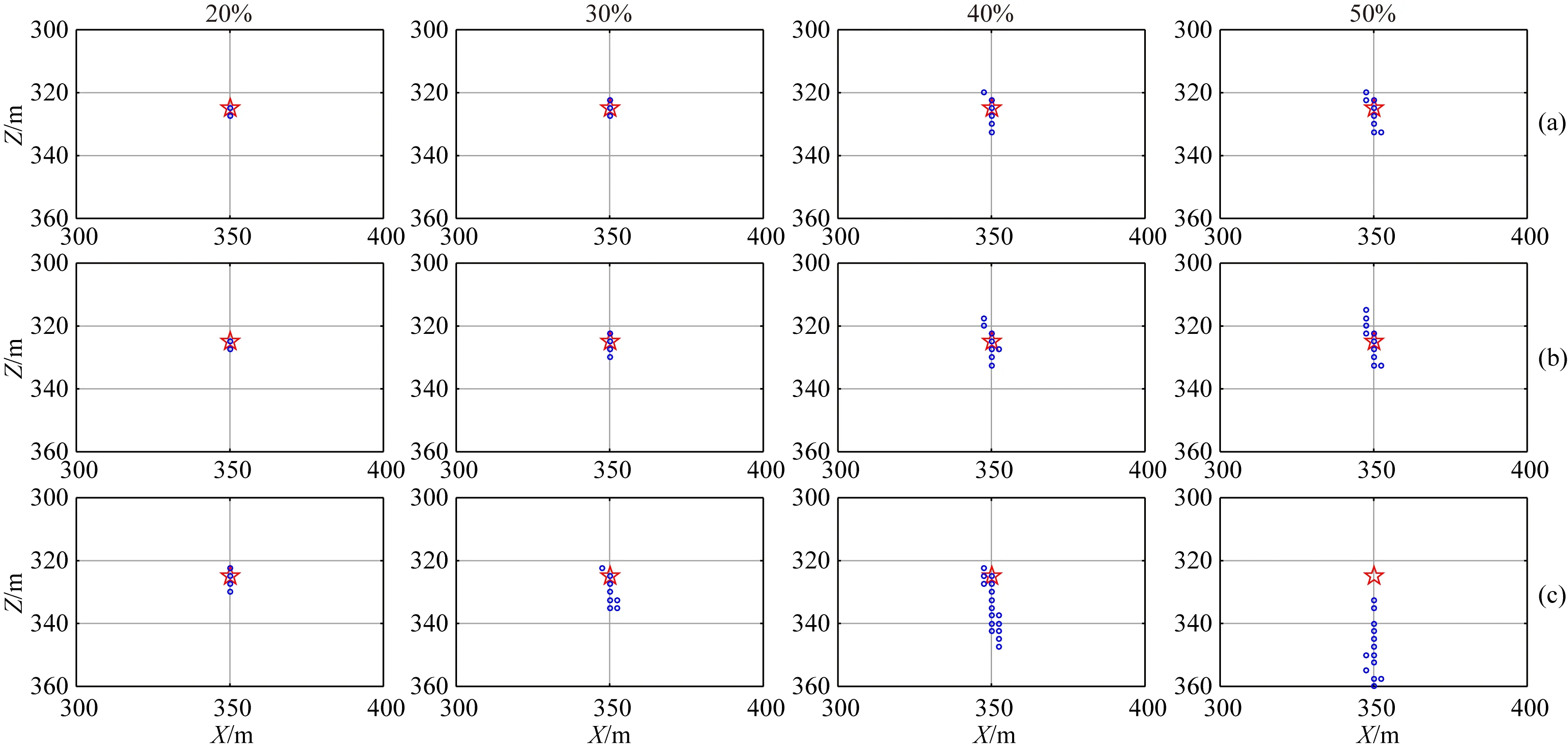
圖7 不同噪聲條件下的100次蒙特卡洛模擬的定位結(jié)果 (a) 互相關(guān)相位加權(quán)成像法； (b) 基于絕對值干涉成像法； (c) 基于長短時窗能量比干涉成像法.Fig.7 Location results of Monte Carlo simulation by 100 times under different noise conditions (a) CCPW; (b) AII; (c) SLII.

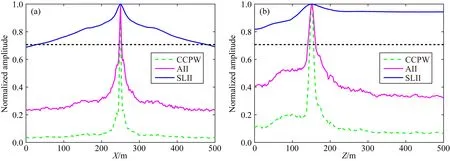
圖8 三種方法的成像剖面中過震源位置的歸一化成像值曲線對比 (a) 水平方向(X)； (b) 垂直方向(Z).Fig.8 Comparison of normalized imaging value curves passing through the source location in imaging profiles of three methods (a) Horizontal direction (X); (b) Vertical direction (Z).

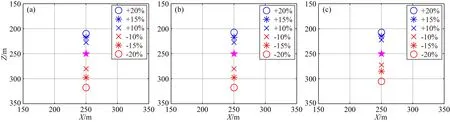
圖9 三種方法在六種速度模型下的定位結(jié)果對比(品紅色五角星為正確震源位置) (a) 互相關(guān)相位加權(quán)成像法； (b) 基于絕對值干涉成像法； (c) 基于長短時窗能量比干涉成像法.Fig.9 Comparison of location results of three methods under six velocity models (The magenta pentagram represents the correct source location) (a) CCPW; (b) AII; (c) SLII.

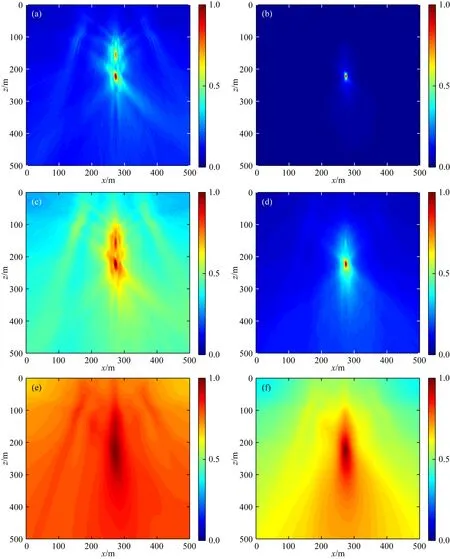
圖10 三種方法利用不同震相組合的成像結(jié)果 (a,c,e) 只利用Vz分量中P波的成像結(jié)果; (b,d,f) 同時利用Vx分量的S波和Vz分量的P波的成像結(jié)果. (a,b) 互相關(guān)相位加權(quán)成像法； (c,d) 基于絕對值干涉成像法； (e,f) 基于長短時窗能量比干涉成像法.Fig.10 Imaging results of three methods using different seismic phase combinations (a,c,e) The imaging results using only the P wave in the Vz component; (b,d,f) The imaging results using the S wave in the Vx component and the P wave in the Vz component at the same time. (a,b) CCPW; (c,d) AII; (e,f) SLII.

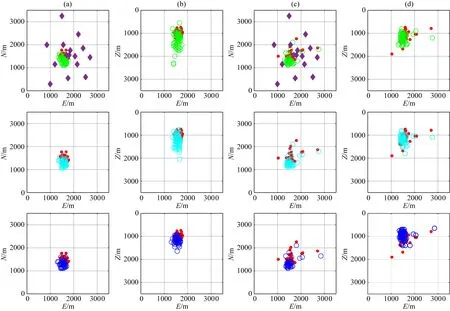
圖11 三種方法對100個強微地震事件在(a)E-N平面和(b)E-Z平面內(nèi)的定位結(jié)果和 100個弱微地震事件在(c)E-N平面和(d)E-Z平面內(nèi)的定位結(jié)果 其中，紅色圓點代表走時反演得到的震源位置，綠色、青色和藍(lán)色圓圈分別代表互相關(guān)相位加權(quán)成像法、 基于絕對值干涉成像法和基于長短時窗能量比干涉成像法的定位結(jié)果，紫色菱形代表檢波器.Fig.11 Location results of 100 strong microseismic events in (a) E-N plane and (b) E-Z plane and 100 weak microseismic events in (c) E-N plane and (d) E-Z plane obtained by three methods The red dots represent the source locations obtained by travel time inversion, the green, cyan, and blue circles represent the location results of CCPW, AII, and SLII, respectively, and the purple diamonds represent the receivers.

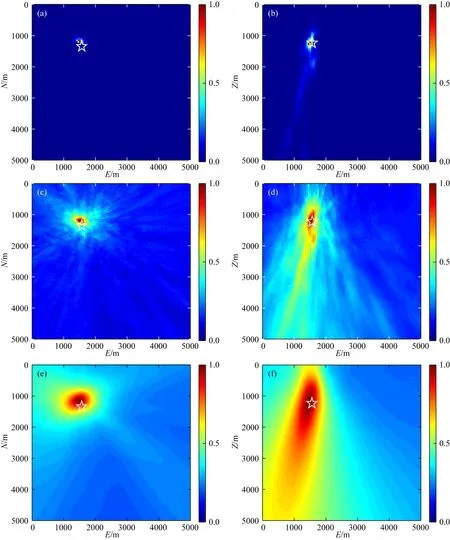
圖12 三種方法對序號為10的弱微地震事件的成像結(jié)果(白色五角星為走時反演定位結(jié)果) (a，b) 互相關(guān)相位加權(quán)成像法； (c，d) 基于絕對值干涉成像法； (e，f) 基于長短時窗能量比干涉成像法.Fig.12 Imaging results of No.10 weak microseismic event obtained by three methods (The white pentagram represents the source location obtained by travel time inversion) (a，b) CCPW; (c，d) AII; (e，f) SLII.

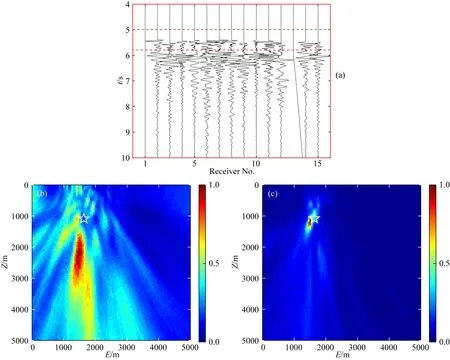
圖13 (a) 序號為90的強微地震事件的Vz分量波形圖；互相關(guān)相位加權(quán)成像法分別對紅色實線框和 紅色虛線框內(nèi)波形得到的關(guān)于P波成像的垂直剖面圖(b)和(c)(白色五角星為走時反演定位結(jié)果).Fig.13 (a) Waveforms of Vz component of the No. 90 strong microseismic event; (b) and (c) Vertical imaging profiles for P-waves in the red solid line border and red dashed line border obtained by CCPW (The white pentagram represents the source location obtained by travel time inversion).

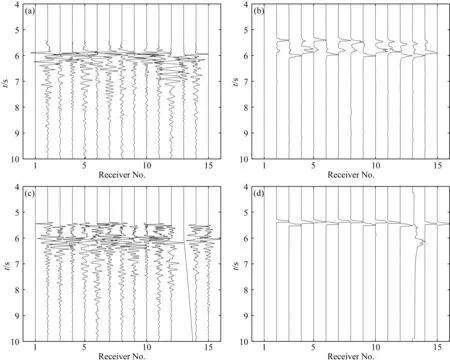
圖14 序號為90的強微地震事件的(a)Vx分量； (b) 經(jīng)STA/LTA處理后的水平分量； (c) Vz分量； (d) 經(jīng)STA/LTA處理后的Vz分量Fig.14 (a) Vx component； (b) horizontal component processed by STA/LTA； (c) Vz component ； (d) Vz component processed by STA/LTA of the No.90 strong microseismic event

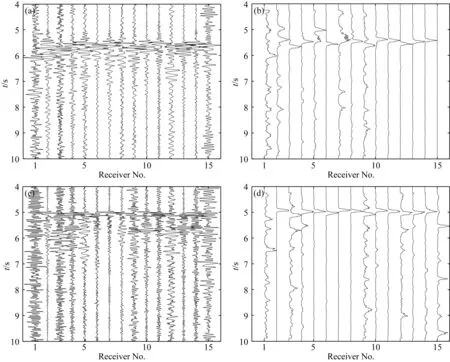
圖15 序號為10的弱微地震事件的(a) Vx分量； (b) 經(jīng)STA/LTA處理后的水平分量； (c) Vz分量； (d) 經(jīng)STA/LTA處理后的Vz分量Fig.15 (a) Vx component； (b) horizontal component processed by STA/LTA； (c) Vz component and (d) Vz component processed by STA/LTA of the No.10 weak microseismic event

表3 六種速度模型下三種方法定位結(jié)果的絕對誤差對比 (單位：m)Table 3 Absolute error comparison of location results of three methods under six-velocity models (Unit: m)

2.2.4 震相數(shù)量

向震源S4的各道原始波形中添加了所有道波形最高振幅的均方差20%的高斯隨機噪聲，測試震相數(shù)量對三種方法定位結(jié)果的影響.圖10中三種方法的成像結(jié)果表明：同時利用Vz分量中P波和Vx分量中S波的定位結(jié)果(圖10b,d,f)的偽像壓制效果要好于僅利用Vz分量中P波的定位結(jié)果(圖10a,c,e).各分量的互相關(guān)波形中包含的震相對信息有[P-S，P-P，S-S，S-P]，在利用P波走時差對互相關(guān)波形中P-P波振幅進行偏移疊加定位時，會將S-S波等其他強相干波的振幅偏移在其他未知的位置上，形成相干偽像.而STA/LTA方法進行了P波和S波震相識別，此時P波的能量得到加強，在一定程度上可能會削弱同分量中S波的相干干擾.

在加權(quán)彈性波干涉成像方法中，可以根據(jù)實際各震相的強弱選取不同加權(quán)系數(shù)進行成像，平衡互相關(guān)波形中多震相信息的約束和干擾(Li et al., 2015, 2018; 田宵等，2020).本文僅同時利用Vx分量中S波和Vz分量中P波成像，也就是Vx分量和Vz分量中的震相組合[P-S，P-P，S-S，S-P]的權(quán)值分別取為[0 0 1 0]和[0 1 0 0].

基于上述數(shù)值算例的處理結(jié)果，可將本文研究的各種方法的性能總結(jié)如表4.

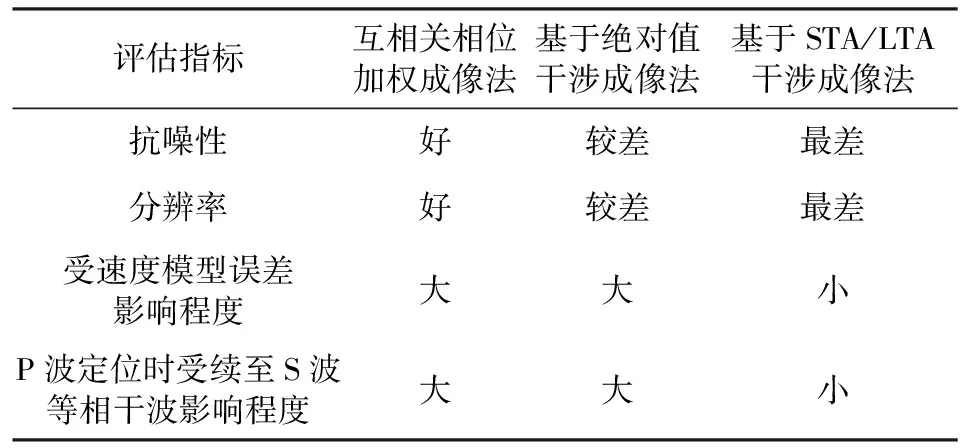
表4 三種方法性能總結(jié)Table 4 Summary of the performance of three methods

3 礦震地面監(jiān)測實際數(shù)據(jù)

本部分將利用礦震監(jiān)測數(shù)據(jù)考察本文提出方法的應(yīng)用效果，并將定位結(jié)果與走時反演定位結(jié)果、基于絕對值干涉成像法和基于STA/LTA干涉成像法的定位結(jié)果作對比.

礦震監(jiān)測臺網(wǎng)HAMNET是2006—2007年間布設(shè)于德國魯爾地區(qū)某煤礦的短期監(jiān)測平臺，包括15個三分量地面地震監(jiān)測臺站.縱波速度為3880 m·s-1，橫波速度為2180 m·s-1(Grigoli et al., 2013)，速度模型建立的網(wǎng)格點數(shù)為101×101×101，網(wǎng)格間距為50 m，時間采樣間隔為5 ms.在監(jiān)測臺網(wǎng)HAMNET實際監(jiān)測到的多個誘發(fā)地震事件中，選取了100個強事件(震級ML>0.5)和100個弱事件(震級ML=-0.8)(Li et al., 2018).基于均勻速度模型，所選取的200個微地震事件基于手動初至拾取的走時反演定位結(jié)果如圖11中紅色圓點所示.為確保波形疊加類定位結(jié)果與走時反演結(jié)果的可比性，波形疊加類方法對這200個事件定位時仍基于上述均勻速度模型.互相關(guān)相位加權(quán)成像法中的指數(shù)v取為4，STA/LTA的長、短時窗分別取250 ms和125 ms.為了提高定位效率，所有事件的波形經(jīng)過震相識別后均截取包含微地震事件的6 s波形進行定位.

100個強微地震事件和100個弱微地震事件的定位結(jié)果對比如圖11所示，弱微地震事件在定位前經(jīng)過了5～30 Hz的帶通濾波處理.其中，三種方法對序號為10 的弱微地震事件的成像結(jié)果如圖12所示，三種方法均能夠較好的定位出該事件的位置，而互相關(guān)相位加權(quán)成像法具有較高的成像分辨率，偽像得到了很好的壓制.

從以上200個現(xiàn)場礦震事件的定位結(jié)果看，尤其是強事件的定位結(jié)果，從原始波形幅度信息出發(fā)進行定位的基于絕對值干涉成像法和互相關(guān)相位加權(quán)成像法的定位結(jié)果，相比于走時反演法和基于STA/LTA干涉成像法的定位結(jié)果在垂直剖面上有很大的分散性，分析其可能存在的原因是：

(1)Vz分量中高幅值S波等續(xù)至相干波干擾.正如數(shù)值模擬分析的一樣，在利用基于絕對值干涉成像法和互相關(guān)相位加權(quán)成像法進行定位時，Vz分量中較強的續(xù)至S波和反射波等，會在最終成像結(jié)果中引入相干干擾.序號90的強事件為互相關(guān)相位加權(quán)成像法定位偏差較大的事件之一，其Vz分量如圖13a所示.以互相關(guān)相位加權(quán)成像法利用該事件Vz分量得到的關(guān)于P波干涉成像剖面為例，即對圖13a中紅色實線矩形框內(nèi)的波形進行關(guān)于P波的干涉成像，結(jié)果如圖13b所示，由于續(xù)至在P波之后的高幅值S波和反射波等震相的相干干擾，震源被定位在了錯誤的位置上.但當(dāng)將S波截掉，只保留P波震相定位時，即對圖13a中紅色虛線矩形框內(nèi)的波形進行關(guān)于P波的干涉成像，結(jié)果如圖13c所示，震源位置與走時反演結(jié)果非常接近.而當(dāng)利用STA/LTA進行定位時，如圖14d中序號為90的強事件經(jīng)過STA/LTA處理后的Vz分量和圖15d中序號為10的弱事件經(jīng)過STA/LTA處理后Vz分量所示，經(jīng)過震相識別后的Vz分量中P波能量得到了強化，且由于此時P波和S波相距較近，最早到達(dá)的P波降低了STA/LTA對后續(xù)S波識別的敏感度，這不僅削弱了Vz分量中S波對定位結(jié)果的影響，同時還使得對Vx和Vy分量中S波能量的識別產(chǎn)生了一定干擾，有些道甚至無法識別，如圖14b和圖15b所示，并且這種影響隨著P波和S波之間的距離越近而越大.同時，某些隨機噪聲和高頻脈沖也會導(dǎo)致STA/LTA對非微地震信號的誤判，如圖15(b，d)所示.

(2)用于定位的S波速度模型不準(zhǔn)確.通過理論分析能夠知道基于絕對值干涉成像法和互相關(guān)相位加權(quán)成像法的分辨率較高，導(dǎo)致對速度模型誤差的敏感度比基于STA/LTA干涉成像法更高，這可能給這兩種定位方法的最終結(jié)果帶來較大的偏差.

4 結(jié)論

本文提出了一種基于原始互相關(guān)波形的振幅和瞬時相位的微地震干涉成像方法——互相關(guān)相位加權(quán)成像法，并結(jié)合數(shù)值算例和現(xiàn)場數(shù)據(jù)深入對比分析了互相關(guān)相位加權(quán)成像法、基于絕對值干涉成像法和基于STA/LTA干涉成像方法.

互相關(guān)相位加權(quán)成像法通過重新組合原始互相關(guān)波形的振幅與瞬時相位信息校正了波形極性變化，無需特征函數(shù)處理，相比基于絕對值干涉成像法和基于STA/LTA干涉成像法，具有更高的成像分辨率和抗噪性.同時由于分辨率的提高，也導(dǎo)致了新方法對速度模型誤差敏感.研究還表明新方法與其他基于波形振幅信息定位的方法一樣，定位結(jié)果容易受波形中較強的續(xù)至波等相干波的影響，本文中當(dāng)利用弱震相P波定位時，同分量中續(xù)至的強震相S波等相干波會導(dǎo)致定位結(jié)果出現(xiàn)偏差.

致謝感謝三位匿名審稿專家提供的寶貴審稿意見和期刊編輯的修改.感謝HAMNET項目組公開實際礦震數(shù)據(jù)(https:∥www.fdsn.org/networks/detail/Z2_2006/).