中學(xué)數(shù)學(xué)研討學(xué)教法課堂教學(xué)模式研究

【摘要】中學(xué)數(shù)學(xué)研討學(xué)教法課堂教學(xué)模式研究介紹了中學(xué)數(shù)學(xué)研討學(xué)教法產(chǎn)生的背景與原因，論述了在課堂教學(xué)中“學(xué)”與“教”的辯證關(guān)系，重點介紹研討學(xué)教法課堂教學(xué)、解題教學(xué)、概念教學(xué)的一般模式，也介紹了研討學(xué)教法的其他簡化模式，并對中學(xué)數(shù)學(xué)課堂教學(xué)模式提出新的思考與評價。

【關(guān)鍵詞】學(xué)教法;課堂教學(xué);模式研究

中學(xué)數(shù)學(xué)研討學(xué)教法主要源于筆者個人專業(yè)成長的經(jīng)歷，受啟發(fā)于作坊教育和基于對當(dāng)前中外中學(xué)數(shù)學(xué)教育的比較性思考。從1987年開始，本人一直立足于中學(xué)數(shù)學(xué)教育教學(xué)實踐，以課堂為現(xiàn)場，以教學(xué)為中心，從實際出發(fā)，不斷深入開展研討學(xué)教法課堂教學(xué)實踐。經(jīng)過多年的摸索與研究，逐步將“高中數(shù)學(xué)研討學(xué)習(xí)法”“高中數(shù)學(xué)研討教學(xué)法”轉(zhuǎn)變升華為“中學(xué)數(shù)學(xué)研討學(xué)教法”，從“教學(xué)法”到“學(xué)教法”，不僅僅是“學(xué)”與“教”互換位置，課堂教學(xué)過程中的主客關(guān)系也發(fā)生了本質(zhì)性變化。把“學(xué)”提升到教學(xué)主體地位，不僅有利于充分調(diào)動學(xué)生的主觀能動性，激發(fā)深藏在學(xué)生骨子里的學(xué)習(xí)潛能，營造濃厚的研討學(xué)氛圍，而且能培養(yǎng)學(xué)生創(chuàng)新意識，提升學(xué)生創(chuàng)新能力，從而產(chǎn)生生成性的教學(xué)效果。而教師作為教學(xué)過程的頂層設(shè)計者，在組織教學(xué)、問題診斷、是非甄別、發(fā)現(xiàn)實證、質(zhì)疑批判等方面都要發(fā)揮其專業(yè)素養(yǎng)的引領(lǐng)作用。在研討學(xué)教法中，“學(xué)”與“教”形成了一種和諧的對立統(tǒng)一關(guān)系。本文主要介紹中學(xué)數(shù)學(xué)研討學(xué)教法課堂教學(xué)的模式研究。

一、研討學(xué)教法課堂教學(xué)一般模式

研討學(xué)教法課堂教學(xué)一般模式是研討學(xué)教法的基本結(jié)構(gòu)系統(tǒng)。它是針對課堂教學(xué)的有效性、科學(xué)性和前瞻性特點進(jìn)行反復(fù)實踐與研究的結(jié)果，是對課堂教學(xué)規(guī)律充分認(rèn)識與思考基礎(chǔ)上，通過科學(xué)抽象而得到的基本思維和操作流程。構(gòu)建模式可由圖1解析：

研討學(xué)教法課堂教學(xué)一般以單元教學(xué)或微專題教學(xué)為主，把各模塊分成若干單元，又將單元分解為幾個課題或微專題，然后根據(jù)課題或微專題的內(nèi)容、性質(zhì)、應(yīng)用等，搜索相關(guān)的教材（不限于當(dāng)版教材）、資料、文獻(xiàn)，并整理成課程素材。接著擬定研討提綱，將“課題研討提綱下達(dá)與課程素材反饋雙向卡”（以下簡稱“雙向卡”）提前發(fā)放給學(xué)生，通過分析研討學(xué)教法課堂的研討過程（常規(guī)變式、引申、鞏固性訓(xùn)練）形成淺層次教學(xué)資源，這是研討學(xué)教法的一條常規(guī)路徑。研討學(xué)教法還有一條教學(xué)生成性路徑，這是它的獨特之處。即：通過對淺層次教學(xué)資源進(jìn)行思考、質(zhì)疑、批判、改進(jìn)，從而生成新素材，再進(jìn)入核心環(huán)節(jié)研討學(xué)教法課堂進(jìn)行研討，通過研討過程再度增強學(xué)生的創(chuàng)新意識。經(jīng)過反復(fù)實踐，我們發(fā)現(xiàn)，通過歸檔與歸納，不僅有利于生成深層次教學(xué)資料，而且還能充實課堂素材，便于推陳出新。

二、研討學(xué)教法解題教學(xué)一般模式

數(shù)學(xué)解題教學(xué)是無法回避的現(xiàn)實問題，尤其是畢業(yè)班復(fù)習(xí)教學(xué)。研討學(xué)教法倡導(dǎo)科學(xué)性、階段性、一般性的解題教學(xué)，不是在淺層次的層面上花大量時間刷題而得到機械解題方法，而是在深層次層面上，通過規(guī)律摸索、課堂研討得到一般性、適應(yīng)性、簡捷性的解題方法。在長期的研討學(xué)教法課堂教學(xué)中，本人逐漸摸索出了研討學(xué)教法解題教學(xué)的一般模式（如圖2）：

研討學(xué)教法解題教學(xué)有三個認(rèn)識境界。

第一個境界是感性認(rèn)識境界，見題解題，對題目不作任何發(fā)散性思考與條件追究，僅滿足常規(guī)性教學(xué)境界。第二個境界，作簡單變式與含參討論，不作一般性研究，滿足小發(fā)現(xiàn)小創(chuàng)新。第三個境界，遵循認(rèn)識事物的規(guī)律：①先獲得感性認(rèn)識。②把感性認(rèn)識上升到理性認(rèn)識。③運用理性認(rèn)識來指導(dǎo)具體實踐。這是解題的最高境界，不僅能整體把握事物發(fā)展的規(guī)律，而且達(dá)到深層次解題教學(xué)的終極目標(biāo)。

三、研討學(xué)教法概念教學(xué)一般模式

數(shù)學(xué)概念教學(xué)是課堂教學(xué)中很重要的環(huán)節(jié)，數(shù)學(xué)概念形成也要基于以問題為導(dǎo)向，以需求為牽引，通過研討學(xué)教的方法幫助學(xué)生形成正確、辯證、本質(zhì)的數(shù)學(xué)概念，尤其對于較抽象的數(shù)學(xué)概念更要突出這三點，概念教學(xué)既研討學(xué)教法課堂教學(xué)的一般性，也研究它的特殊性。它的一般模式是（圖4）：

第一階段：課前準(zhǔn)備。教師要認(rèn)真研討《中學(xué)數(shù)學(xué)課程標(biāo)準(zhǔn)》與數(shù)學(xué)現(xiàn)行教材，上網(wǎng)查找相關(guān)文獻(xiàn)資料，學(xué)習(xí)借鑒其他版本教材如何處理概念等問題，類比參考相關(guān)已知內(nèi)容，撰寫研討學(xué)教法課堂教學(xué)雙向卡，課前提供給學(xué)生。

第二階段：課堂教學(xué)。這是研討學(xué)教法課堂的核心階段。教師在對教材進(jìn)行思考、批判、改進(jìn)等方面的處理中，形成符合學(xué)生認(rèn)知、符合客觀規(guī)律的數(shù)學(xué)概念。師生共同參與課堂研討學(xué)教過程，通過概念的引申、辨析、遷移，從而幫助學(xué)生加強對概念深層次的理解。

第三階段：課后功課。主要落實三方面任務(wù)：學(xué)生要完成歸納小結(jié)，做適當(dāng)鞏固性訓(xùn)練題，跟同學(xué)分享學(xué)習(xí)心得;教師要跟進(jìn)輔導(dǎo)，即時解答學(xué)生的存疑，指導(dǎo)學(xué)生每天寫一問一議的筆記;單元教學(xué)結(jié)束時，學(xué)生需要完成單元檢測試題或撰寫小論文。

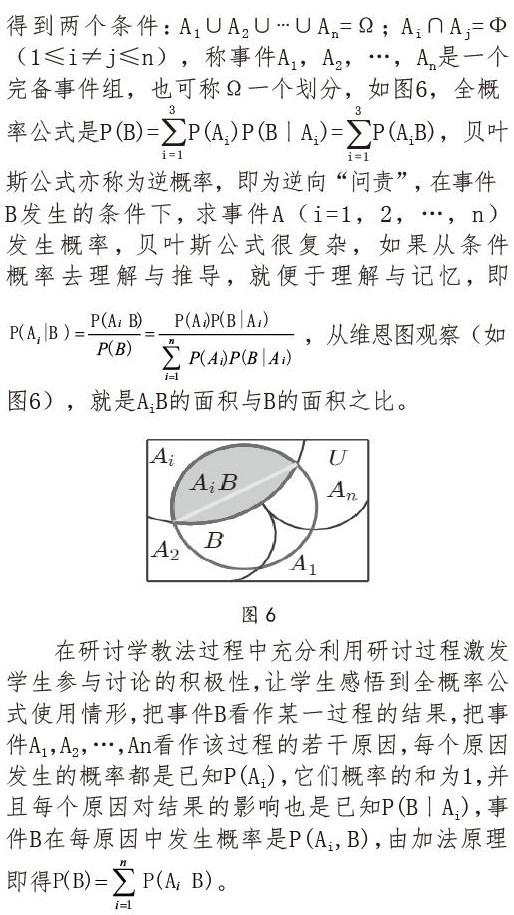
譬如“全概率公式與貝葉斯公式”的教學(xué)，先認(rèn)真研讀課程標(biāo)準(zhǔn)，課程標(biāo)準(zhǔn)要求“結(jié)合古典概型，會利用全概率公式計算概率。了解貝葉斯公式。”并建議“在概率的教學(xué)中，應(yīng)引導(dǎo)學(xué)生通過具體實例”，理解全概率公式的內(nèi)涵與外延，查閱他版教材（新增內(nèi)容還需要查閱大學(xué)教材）并與當(dāng)版教材的概念引入、例題設(shè)計、公式推導(dǎo)做比較，做好“雙向卡”提前發(fā)給學(xué)生。下面例說全概率公式和貝葉斯公式教學(xué)。

研討學(xué)教法跟進(jìn)過程也是非常重要的，既有常規(guī)性歸納小結(jié)、鞏固訓(xùn)練，也有思辨性存疑待解、一問一議，更有創(chuàng)新性收獲展示、論文習(xí)作等檢驗成效的學(xué)習(xí)活動，每單元教學(xué)結(jié)束時，安排兩個學(xué)習(xí)小組在教室墻板展示收獲所得，主要展示問題的創(chuàng)新解法。

研討學(xué)教過程中，如果能激活學(xué)生的學(xué)習(xí)探索潛能，令學(xué)生產(chǎn)生了前瞻性、開創(chuàng)性的想法，那么就可以進(jìn)一步要求學(xué)習(xí)小組合作撰寫數(shù)學(xué)小論文，這樣不僅能讓學(xué)生感受到數(shù)學(xué)學(xué)習(xí)的成功喜悅，而且提升學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，增強學(xué)習(xí)的自信心，讓學(xué)生充分感受到數(shù)學(xué)的內(nèi)在美。

四、研討學(xué)教法其他簡化模式簡介

學(xué)教法最大優(yōu)勢在于能充分發(fā)揮學(xué)生的學(xué)習(xí)主觀能動性，提高學(xué)生的課堂教學(xué)的關(guān)注度和參與度。學(xué)教法是在目標(biāo)、任務(wù)驅(qū)動下，要求學(xué)生通過預(yù)習(xí)與查找資料，按“雙向卡”上的提綱先預(yù)習(xí)后學(xué)習(xí)，并提出自己的想法與建議，充分發(fā)揮學(xué)生的主體作用。學(xué)教法還結(jié)合新時代中學(xué)生心理特征，讓課堂成為學(xué)生展示自我的平臺，能激起學(xué)生學(xué)習(xí)動機，激發(fā)學(xué)生的創(chuàng)新意識，生生研討可促成生生思維的互相促進(jìn)，師生研討可促進(jìn)教學(xué)相長，從而實現(xiàn)學(xué)生、教師的“雙發(fā)展”“雙提升”。

當(dāng)然任何教學(xué)模式都是辯證理解與應(yīng)用的，前面介紹了研討學(xué)教法課堂的一般模式，它反映了事物的共性。同時我們要針對不同的學(xué)情、內(nèi)容、學(xué)段、目標(biāo)，選擇不同研討學(xué)教模式來體現(xiàn)事物的個性，簡單介紹如下：

1.“自學(xué)—研討”式教學(xué)模式。實施先自學(xué)后研討策略，通過設(shè)置任務(wù)清單，讓學(xué)生自主學(xué)習(xí)，感悟數(shù)學(xué)，梳理問題，然后組織學(xué)生研討交流，解決疑難問題，教師引領(lǐng)學(xué)生對共性問題進(jìn)行研究，啟發(fā)學(xué)生對可思性問題進(jìn)行拓展與引申，促進(jìn)學(xué)生綜合能力的提升。

2.“問題—研討”式教學(xué)模式。實施問題導(dǎo)向教學(xué)策略，在學(xué)生參與下，把教學(xué)內(nèi)容提煉成一系列問題，以問題為導(dǎo)向引領(lǐng)學(xué)生研討活動，讓學(xué)生在分析問題、解決問題的過程中感受數(shù)學(xué)、理解數(shù)學(xué)，促進(jìn)學(xué)生分析、解決問題能力的提升。

3.“活動—研討”式教學(xué)模式。實施實踐活動教學(xué)策略，把教學(xué)內(nèi)容設(shè)計成實踐研討的對象，讓學(xué)生在實踐研討活動中動手、動腦，親自經(jīng)歷數(shù)學(xué)知識的研討歷程，感受數(shù)學(xué)的研究過程和方法，從而在研討活動中認(rèn)識數(shù)學(xué)，在活動中體驗數(shù)學(xué)。

俗話說，“教學(xué)有法，教無定法，貴在得法！”筆者倡導(dǎo)的中學(xué)數(shù)學(xué)研討學(xué)教法課堂教學(xué)模式是以問題為導(dǎo)向，以研討過程為核心，強調(diào)學(xué)習(xí)方法的靈活多樣，充分調(diào)動學(xué)生學(xué)習(xí)潛能，把學(xué)生骨子里的東西激發(fā)出來，使知識易于接受，問題易于解決，在學(xué)生的積極配合下提高教學(xué)的有效性。這樣既能出教學(xué)成果，又能出科研成果。比如筆者從教以來撰寫的許多論文的素材大多來源于研討教學(xué)中的師生共同發(fā)現(xiàn)。由此可見，這是一件一舉多得、一舉多贏的事，何樂而不為呢？

【參考文獻(xiàn)】

[1]李紅慶.高中數(shù)學(xué)研討學(xué)習(xí)法[M].武漢：華中師范大學(xué)出版社，1995.

[2]李紅慶.跟我學(xué)解高中數(shù)學(xué)題[M]（2版）.哈爾濱：哈爾濱工業(yè)大學(xué)出版社，2021.

[3]史寧中，王尚志.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）解讀[M].北京：高等教育出版社，2018.