非線性不等式約束平差的一種新嶺估計算法
李文娜 宋迎春 鄧 偉 謝雪梅
1 中南大學地球科學與信息物理學院,長沙市麓山南路932號,410083 2 中南林業科技大學土木工程學院,長沙市韶山南路498號,410004
處理測量數據病態問題時常用嶺估計[1]方法,但該方法僅從數學角度對平差模型的病態性進行改善,缺乏對參數實際情況的考慮,難以保證顯著提高平差精度。解決病態問題的另一個思路是充分利用一些基于前期觀測和附加(或額外)的先驗信息。這些附加的先驗信息常表現為參數的約束條件。
近年來國內學者對等式約束[2]、不等式約束[3]、區間約束[4]的平差理論與算法的研究取得了許多新成果。但這些約束基本上都是線性約束,用來描述先驗信息存在明顯不足,對于解決數據處理中的問題也有一定的局限性。楊婷等[5]指出,當系數矩陣具有近似復共線性(模型病態)時,參數的最小二乘估計的長度將在向量空間中的某些方向上偏大,此時一般的線性約束條件不再適合。 最近,學者們提出一種新的非線性約束形式的“二次約束”,如范數約束、球約束和橢球約束,其“二次”特性更容易與平差準則融合,但直接將它們線性化有時會使約束條件失去意義。針對病態問題的非線性不等式約束平差模型的解算,左廷英等[6]提出一種帶有球約束的迭代算法,該算法只對參數進行迭代。在實際應用中,通常采用參數的最小二乘解作為迭代的初始值。但當法方程系數矩陣嚴重病態時,參數的最小二乘解與參數真值相距甚遠,此時不僅會延長迭代的時間,也會降低計算結果的精度。肖兆兵等[7]給出參數帶橢球約束平差的具體算法,該算法獲取高精度解的前提是需要選擇一個合適的拉格朗日乘子迭代初始值。對于不同的觀測數據,應該有不同的初始值,由于缺乏對平差模型的深入了解,該算法通常選取0作為迭代初始值,導致可能會出現迭代不收斂的現象。綜合以上問題,本文基于嶺參數與約束條件有關這一特性,提出一種新的嶺估計算法求解非線性不等式約束平差模型,不僅可以保證迭代收斂,而且還能提高計算效率。
1 非線性不等式約束平差模型及其算法
一般的平差模型可以表示為:
L=AX+e
(1)
式中,L為m×1的線性化后的常數向量,A為m×n的觀測值系數矩陣,設m≥n,rank(A)=n,X為n×1的未知參數向量,e為隨機誤差向量,期望為0(e~N(0,σ2I),Σ=σ2I為協因數矩陣)。
如果參數帶有不確定性,對X加以先驗約束,得到:
式中,‖·‖ 表示二范數,c≥0且已知。根據最小二乘準則,將式(2)轉化為非線性不等式約束最小二乘問題。當X沒有約束時,直接利用最小二乘法可求得參數解為XLS。若‖XLS‖2≤c,則該最小二乘解就是平差問題(2)的解;當系數矩陣病態時,往往有‖XLS‖2>c,式(2)中的非線性不等式約束問題可轉化為非線性等式約束問題:
min(L-AX)T(L-AX)
s.t.‖X‖2=c
(3)
式(3)也可通過凸優化理論得到,因為(L-AX)T(L-AX)是一個凸函數,其最優值將在邊界上取得。使用拉格朗日乘數法求解式(3):
X(λ)=(ATA+λI)-1ATL
(4)
式(4)為通常的嶺估計,其中,λ的取值與觀測值相關,即與參數的先驗信息有關。
為研究λ的確定方法,采用Householder變換將矩陣A進行雙對角化[8]:
式中,P為m階的正交矩陣,Q為n階的正交矩陣,B為n×n的上雙對角矩陣,且B和A的奇異值相同。因此,如果B的奇異值分解為:
B=CSDT
(6)
那么,
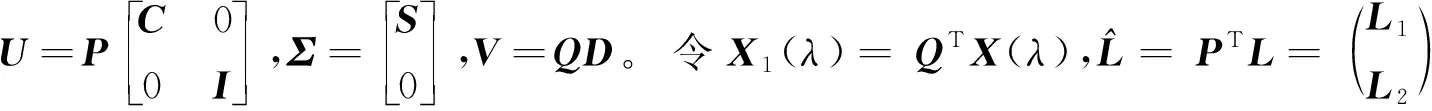
X1(λ)=(BTB+λI)-1BTL1
(7)
式(7)等價于求解:
為減少計算量,利用Givens變換簡化式(8)。設W為Givens矩陣的乘積,即為2n階的正交矩陣,則有:
式中,Bλ為n階的上雙對角矩陣。因此,X1(λ)可由式(10)計算:
BλX1(λ)=Z1
(10)
由X1(λ)=QTX(λ)得‖X(λ)‖2=‖X1(λ)‖2。
設
ω(λ)=‖X(λ)‖2=‖X1(λ)‖2=
將式(6)代入式(11):
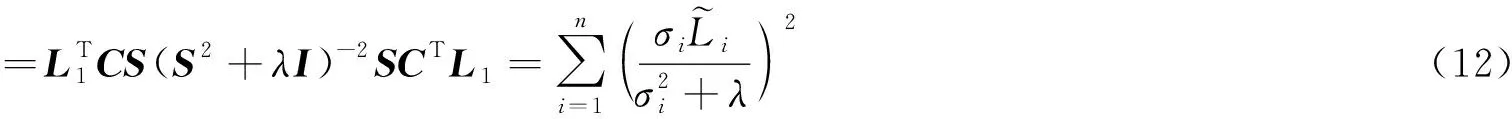
式中,σi為B的奇異值,=CTL1。
顯然, 對于λ>0,ω(λ)是單調遞減函數。由于ω(0)=‖XLS‖2>c,因此存在唯一的λ*>0,使ω(λ*)=c。對于非線性方程ω(λ)=c,很難求得其精確解。通常情況下,求出的λ只需要使‖X1(λ)‖2/c與1足夠接近即可。
根據Halley迭代公式[9]可以得到λ的迭代公式為:
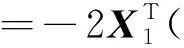
具體迭代步驟為:1)利用先驗信息確定約束值c;2)設定λ的初始值λ0和一個非常小的限值ε;3) 將λn代入式(9)求出Bλn,根據式(10)得到X1(λn),從而求出ω(λn),計算|ω(λn)-c|<ε是否成立,若成立取出X1(λn),則X(λn)=QX1(λn)作為最終解,迭代終止,反之則進行步驟4);4)利用X1(λn)求出ω′(λn)、ω″(λn),然后再利用式(13)求出λn+1,回到步驟3)。
在上述算法中,迭代初始值λ0的確定非常關鍵,只有選取適當的初始值,才能保證其迭代的收斂性,同時提高計算效率。根據上文可知,該算法中嶺參數λ與參數的先驗信息有關,基于此特性,下面推導嶺參數的估計式,將其作為迭代的初始值,并闡述其合理性。
2 參數的確定方法
假設矩陣B的奇異值從大到小排列為:
σ1≥…≥σn-1≥σn
對于測量平差數據處理中的一些病態問題,其系數矩陣中往往會存在一個接近于0的特征值,也就是說σn?σn-1,當n≠0時,有:
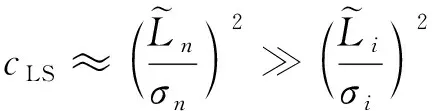
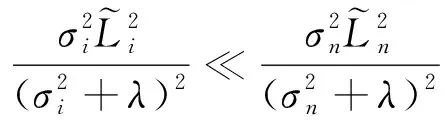
即
由此可得到λ的估計值:
λ*
(14)
ω()的值不會遠大于c,否則令作為迭代初始值相比于0作為迭代初始值的優勢不明顯。
定義一個新函數:
φ(σ)=(σ+/σ)2
由此函數的性質可知,當σ>0時,φ(σ)有唯一的最小值,假設該最小值在σ=σ*處取得,則:
φ′(σ*)=2(σ*+/σ*)(1-/(σ*)2)=0
即
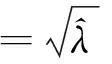
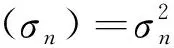
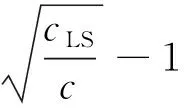
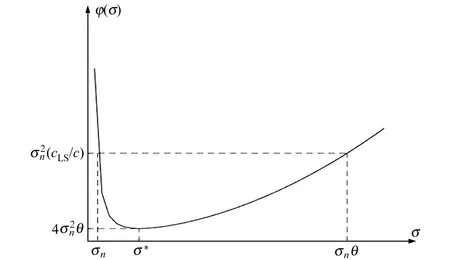
圖1 θ>1時φ(σ)的圖像Fig.1 Image of φ(σ) when θ>1
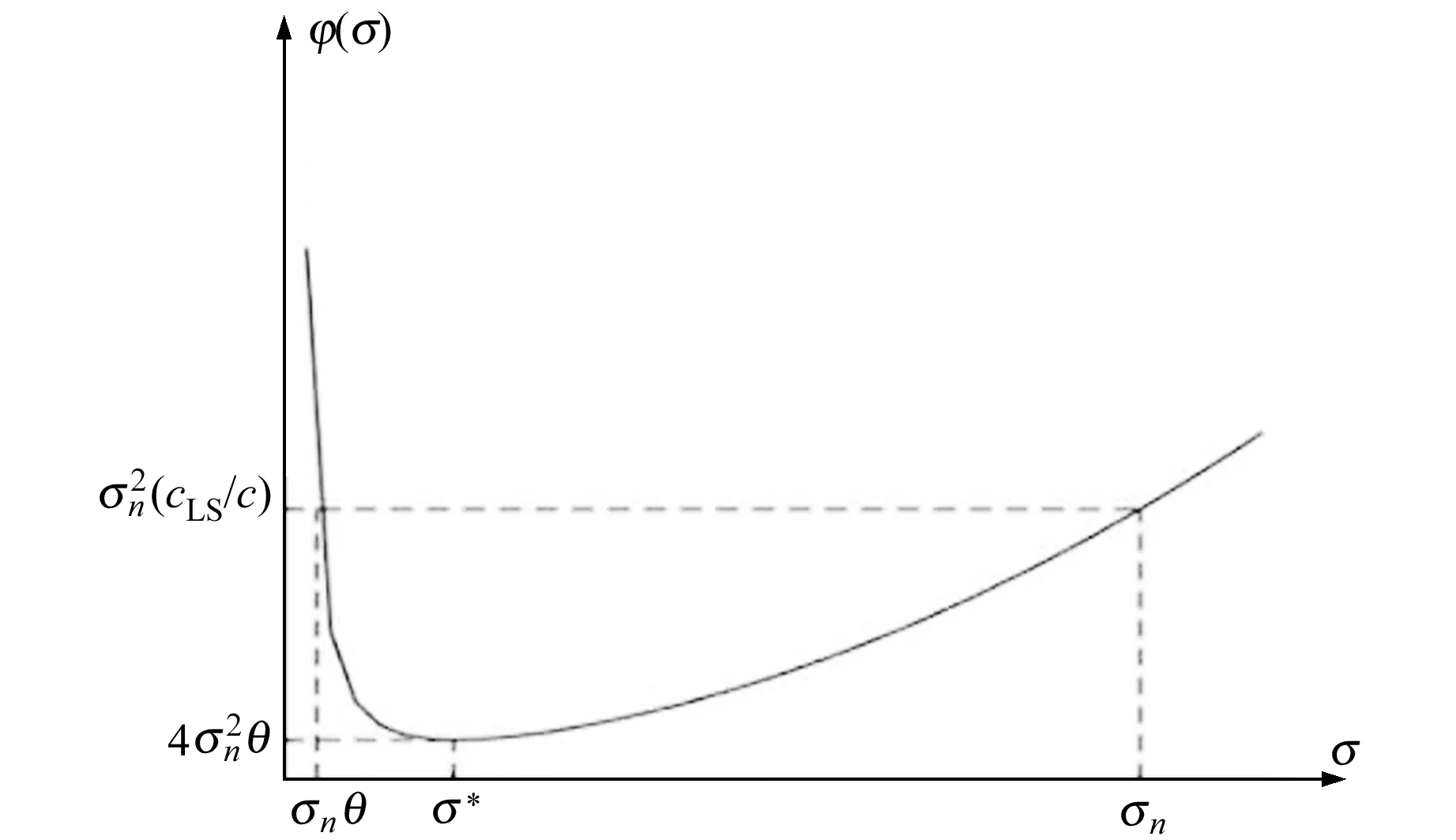
圖2 θ≤1時φ(σ)的圖像Fig.2 Image of φ(σ) when θ≤1
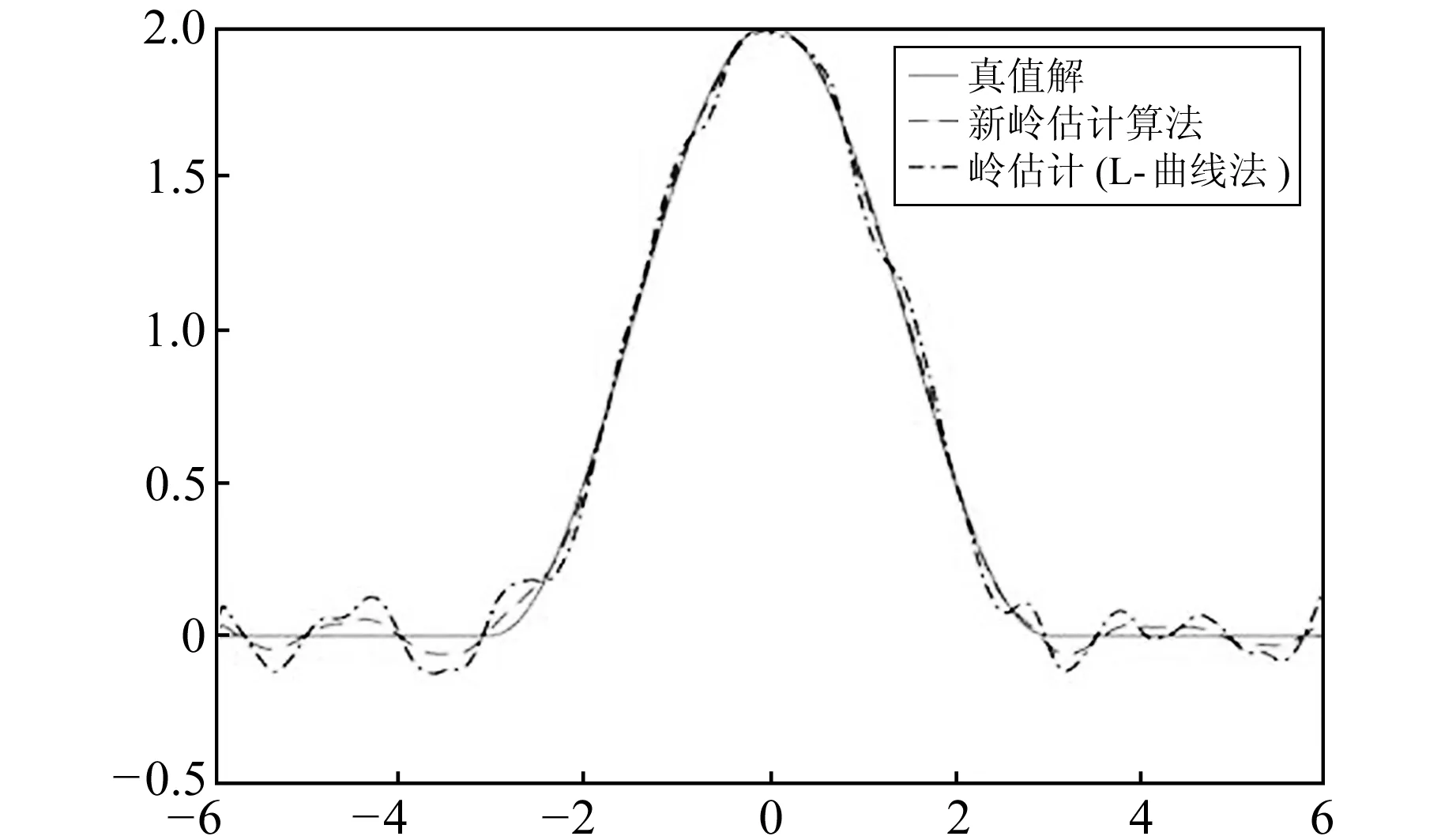
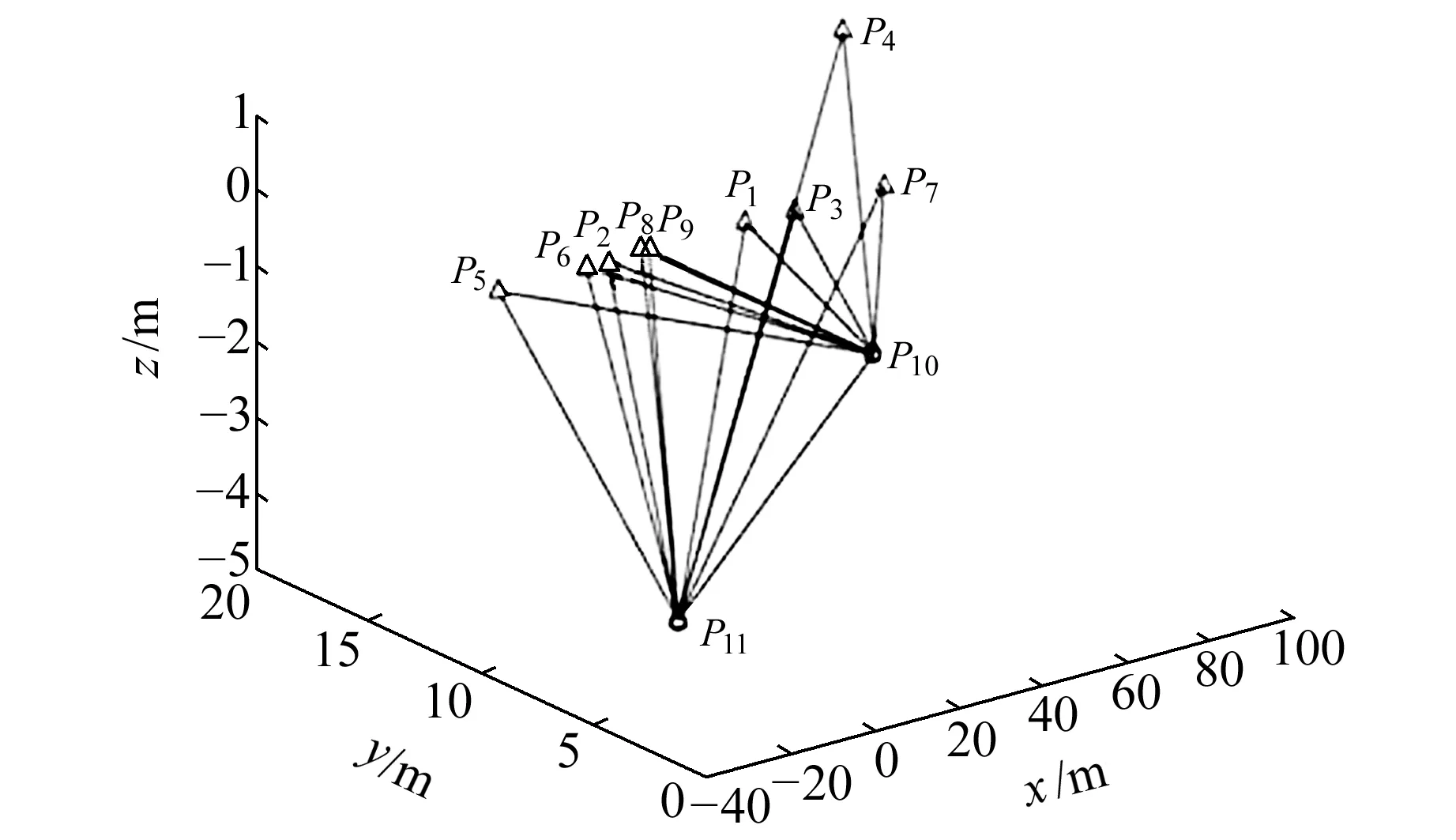
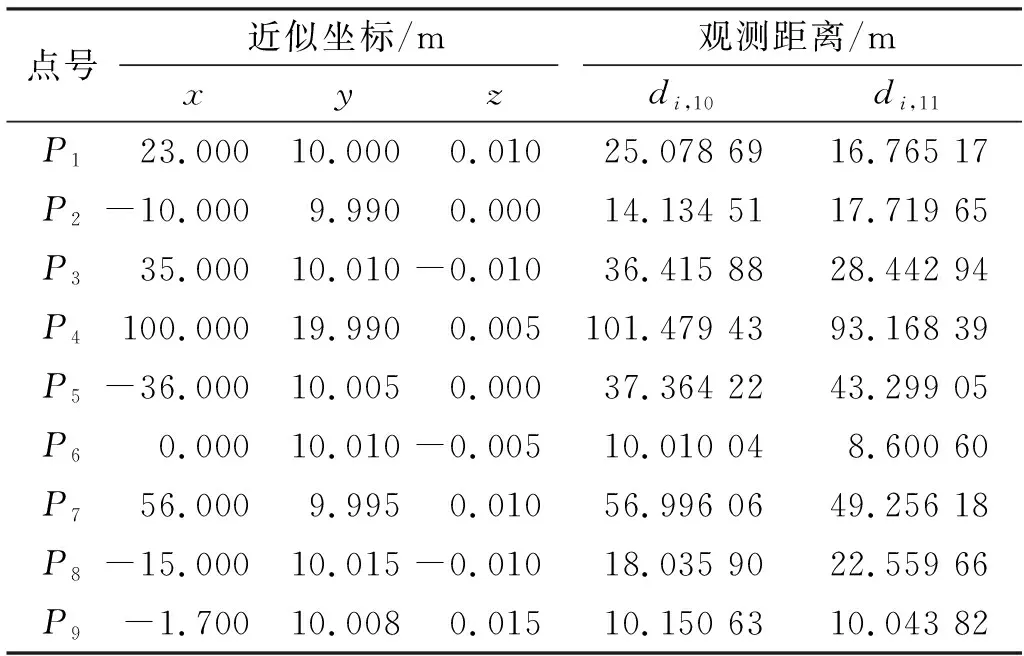
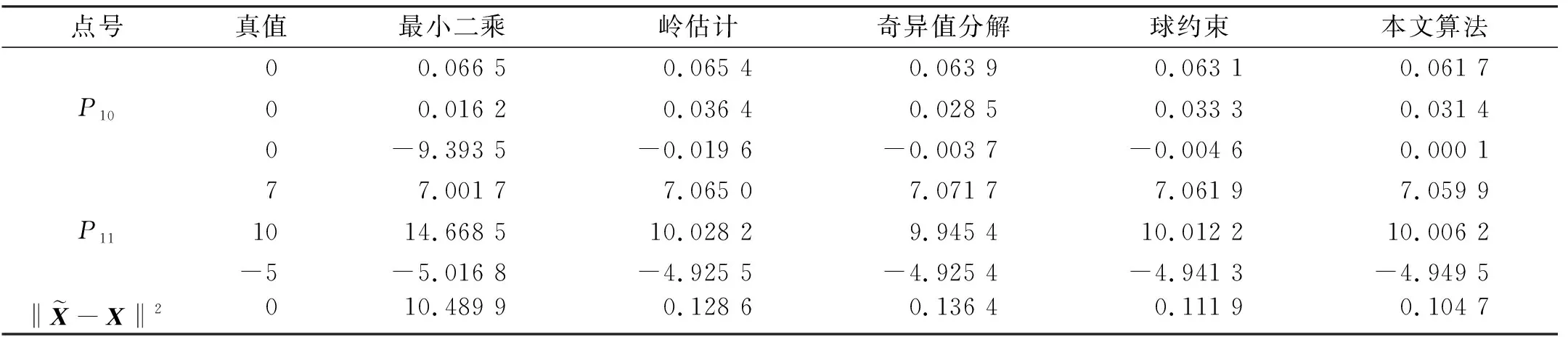
1)假設φ(σi)≥φ(σn),i (σi-σn)(σi-σnθ)≥0 (15) 如果θ≤1,則式(15)成立;如果θ>1,且σi>σnθ,說明B的奇異值分布范圍不在區間Y內,即σi?Y,則式(15)仍成立。在這2種情況下有: 令η=‖‖2/,可以將式(16)簡化為: 即 ‖X1()‖2/c≤η 2)假設θ>1,且B的奇異值有一些分布在區間Y內,則存在: 因此 綜上所述,在θ≤1(cLS≤4c)的情況下,‖X1()‖2/c≤η。在θ>1(cLS>4c)的情況下,當σi?Y(i 為驗證本文新嶺估計算法在處理病態問題中的有效性,采用文獻[10]給出的第一類Fredholm積分方程的具體函數形式模擬數據進行計算,并將所得結果與利用L-曲線法確定嶺參數的嶺估計方法計算的結果進行比較,見圖3。 圖3 本文算法與嶺估計法的比較Fig.3 Comparison of our algorithm and ridge estimation algorithm 從圖3可以看出,用本文方法計算出的函數曲線與真值的函數曲線吻合程度更高,本文方法計算的結果與真值的誤差平方和為0.080 1,而利用嶺估計法計算的結果與真值的誤差平方和達到0.713 6。雖然兩者都能夠對系數矩陣的病態性進行改善,但本文算法考慮了參數的先驗信息,所以精度更高。 病態測邊網見圖4,P10、P11為未知點,假設其坐標真值分別為(0 m,0 m,0 m)和(7 m, 10 m,-5 m),其坐標近似值分別取(0.01 m,-0.01 m,0.02 m)和(7.01 m,9.99 m,-5.01 m)。P1,P2,…,P9為已知點,其坐標及到2個未知點的觀測距離見表1。P10與P11之間的觀測距離為d10,11=13.107 9 m,各觀測量精度相等,中誤差為0.001 m。 圖4 空間測邊網[11]Fig.4 Spatial geodesic netwo 表1 已知點的坐標和邊長觀測值[11]Tab.1 Coordinates of known points and side length observations 表2 各種方法對病態問題解算結果的比較Tab.2 Comparison of solution results among various methods for ill-posed problem 表3 初始值對迭代次數的影響Tab.3 Influence of initial values on the number of iterations 從表3可以看出,將嶺參數的估計式作為迭代的初始值是合理的,不僅能保證迭代收斂,同時還能提高計算效率。 大地測量中存在大量關于參數的先驗信息,利用這些先驗信息對參數加以約束,可以有效改善平差模型的病態性。本文針對參數帶有非線性不等式約束的最小二乘問題,建立相應的平差模型,給出求解該平差模型的一種迭代算法。該算法在解算效率和解算精度上有較明顯的優勢,但由于誤差的隨機性和參數真值的未知性,導致參數的約束范圍通常需要采用前期數據處理的結果來確定,所以此時解算結果的質量會受到前期數據處理提供的先驗信息的影響。通常在實際應用中遇到的問題比函數模型所展示的問題要復雜得多,如何充分利用先驗信息獲取可靠的參數信息,進而提高算法的準確性,是接下來研究工作的重點。
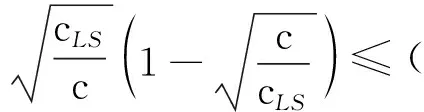
3 數值實驗
3.1 數值模擬實驗
3.2 病態測邊網實驗


4 結 語

