基于雙目視覺的指針儀表讀數識別

涂沛馳，傅鈺雯，熊宇璇，楊健晟

（1貴州大學 電氣工程學院，貴陽 550025；2貴州交通職業技術學院 物流系，貴陽 551400；3貴州大學 外國語學院，貴陽 550025）

0 引 言

隨著科學技術的發展，變電站作為電力系統中不可或缺的一部分，變電站的安全系數及工作效率就變得尤為重要，但由于站內存在電磁干擾等環境因素將對數顯式儀表產生讀數上的影響，因此變電站中的指針式儀表是對特定數據進行采集及監測的重要工具，但到目前為止，大部分變電站內的指針式儀表仍靠人工進行讀數，由于人眼識別讀數存在著工作效率低下、讀數誤差大等缺點，因此實現變電站內指針式儀表的自動化讀數是亟需解決的問題。

隨著計算機圖像處理技術的發展，現如今基于計算機視覺的自動識別技術在儀表讀數中得到了廣泛的應用。張冀等人、曾舒帆等人以及李祖賀等人采用剪影法把2張背景相同、但指針位置不同的圖片進行減法操作，以此來獲取儀表指針的位置。劉迪等人通過改進的Hough變換來識別指針儀表的位置，再根據指針的旋轉角度來計算讀數。針對指針顏色與表盤存在明顯區別，徐洋等人采用了RGB顏色通道與改進的Hough變換相結合的辦法來定位指針的所在位置。這是基于相機正視儀表的情況下所進行的讀數識別，但在許多場景下，由于相機不能完全正視儀表，就會導致拍攝時出現視差的情況，從而使讀數出現較大的誤差。

針對表盤傾斜的狀況，莫文雄等人使用Canny邊緣檢測算子提取刻度盤以及指針輪廓作為模板，再將輸入圖像與模板進行匹配，通過部分區域相似性來計算模板在輸入圖像中的位置，最后利用查表法進行讀數識別。房樺等人首先對儀表圖像建立模板，然后通過SIFT算法提取儀表表盤所在位置，該算法在處理圓形物體時，尋找到的關鍵點較少，耗時長且數據計算量大，針對校正圓形物體存在一定的缺陷。朱柏林等人采用了ORB算法來獲取儀表盤區域，該算法具有較快的運行速度。然而上述方法中，模板的制作需針對同型號儀表，工廠中存在不同種類儀表，全部建立模板工作量大。SIFT算法需要提取圖中的穩定點，適合有明顯角點的矩形儀表，對于工廠中圓形儀表識別較為困難，故上述方法適用性不強。

相對于傳統單目的指針式儀表的讀數識別，雙目視覺及三維重建技術能很好地還原出物體的三維信息，從而消除由視差引起的讀數誤差問題。

在此情況下，提出了一種基于雙目視覺的指針式儀表讀數的識別方法，通過雙目相機獲取指針式儀表視差圖，利用視差圖中的特征點匹配進行三維重建，在重建的三維空間中校正指針與表盤的相對位置，最終實現工業環境下指針式儀表在任何視角下的準確讀數。

1 系統設計方案

本方案采用雙目視覺系統采集傾斜狀態下的指針式儀表的視差圖并進行圖像預處理，接著通過特征點匹配重建出指針與表盤在空間中的位置，此方案的核心是將空間中的指針垂直投影至重建出的表盤平面上，并構建指針角度-儀表讀數模型來計算讀數。針對雙目視覺技術下的指針式儀表的讀數識別，系統設計流程如圖1所示。

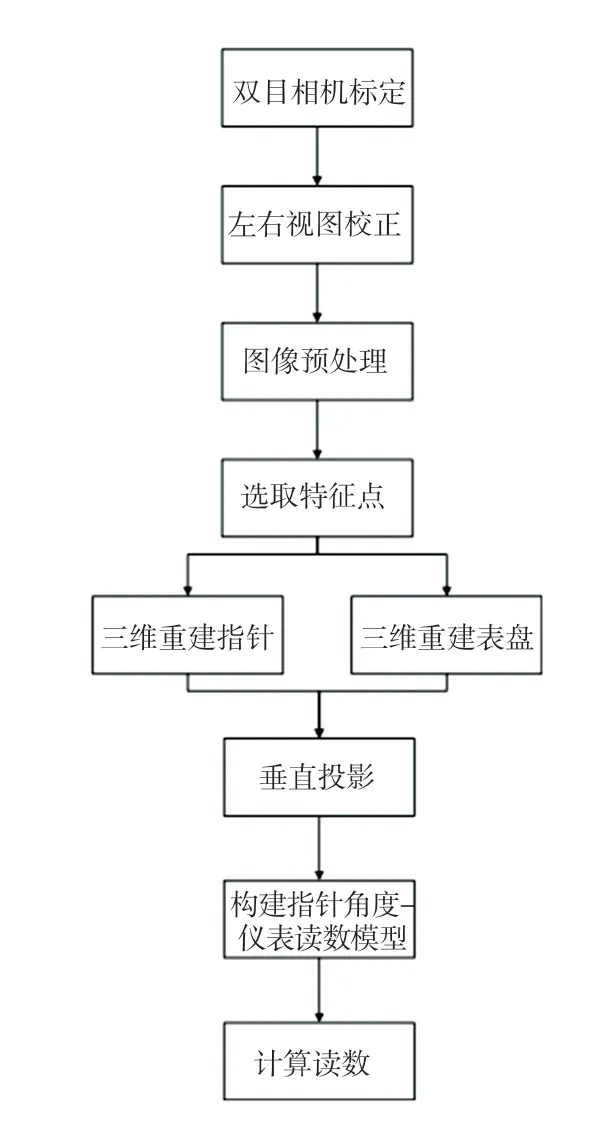
圖1 雙目視覺指針儀表讀數識別流程圖Fig.1 Flow chart for recognition of binocular vision pointer meter readings

2 雙目視覺原理

2.1 雙目視覺計算原理

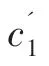
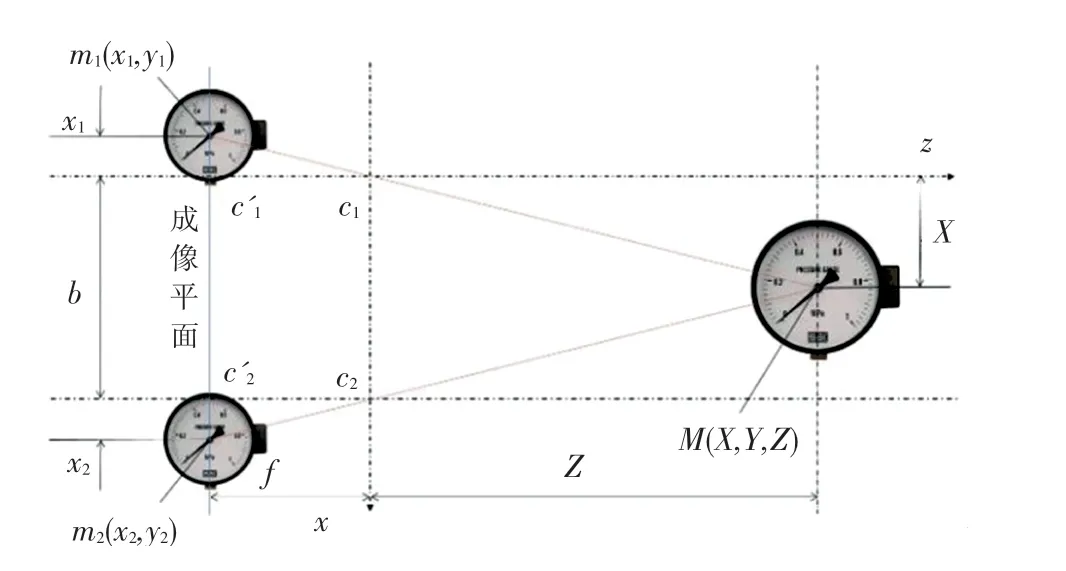
圖2 雙目視覺成像原理圖Fig.2 Principle diagram of binocular vision imaging

由圖2可知，右側儀表上特征點的三維空間坐標為(，，)，該點在左、右相機成像上對應的投影點分別為（，）和（，）。假設左、右相機平行，即。由三角幾何關系，從圖1中可以得到式（1）和式（2）：

由式（1）和式（2）可以獲取到拍攝物體所需要的深度信息為式（3）：

其中，（）為視差，可以通過匹配左、右視圖中的對應特征點獲取。因此，左相機上的任意一點在右相機上找到與之對應的特征點后，便能得到獲取對應物體的深度信息，即三維坐標。由式（3）可以看出，在雙目視覺系統中，當與確定時，深度與視差（）成反比。

2.2相機標定及內外參數

三維重建前需要對相機進行標定，常用的有張氏標定法、傳統標定法等。相機進行標定后，立體空間中任意一點的坐標與相機坐標系下對應點的坐標可以通過式（4）表示：

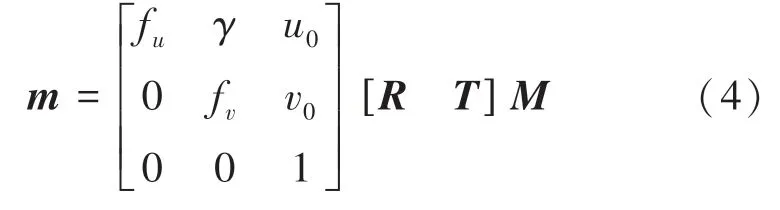
其中，f、f、、、為相機內參；f與f分別為軸和軸上的歸一化焦距；與為光學中心；為圖像坐標與世界坐標的斜交因子；矩陣與矩陣為相機外參，分別表示旋轉矩陣及平移矩陣。

3 實驗過程與數據處理

3.1 雙目相機標定

實驗采用的雙目系統由2臺工業相機組成，配合使用6 mm定焦鏡頭，使用三腳架進行固定拍攝。圖像曝光時間為30 ms，增益為1.25，拍攝11組標定板圖像，標定板的角點識別結果如圖3所示。

圖3 標定板角點識別結果Fig.3 Results of the identification of corner points of the calibration plate

在此基礎上，通過Matlab軟件自帶的stereo Camera Calibrator標定程序對其進行標定以獲取內、外參數，標定后對11組標定板圖像進行三維重建，如圖4所示。重建后的誤差如圖5所示。

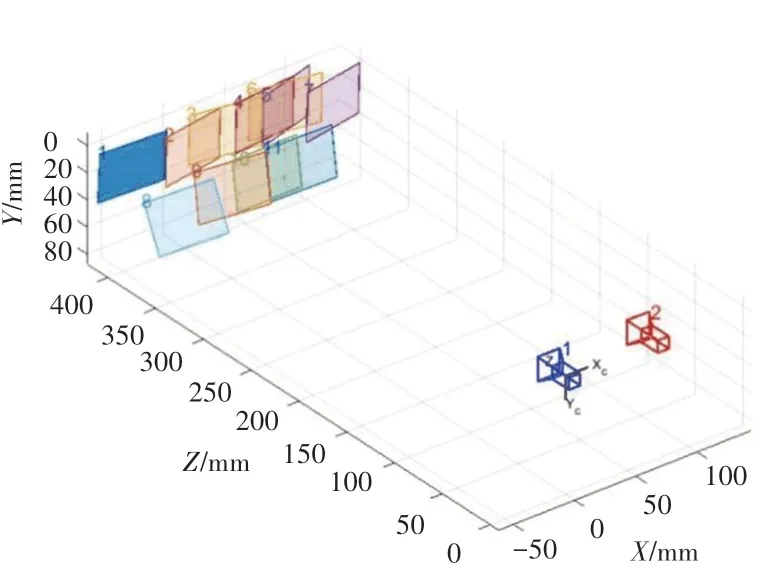
圖4 標定板三維重建Fig.4 3D reconstruction of the calibration plate

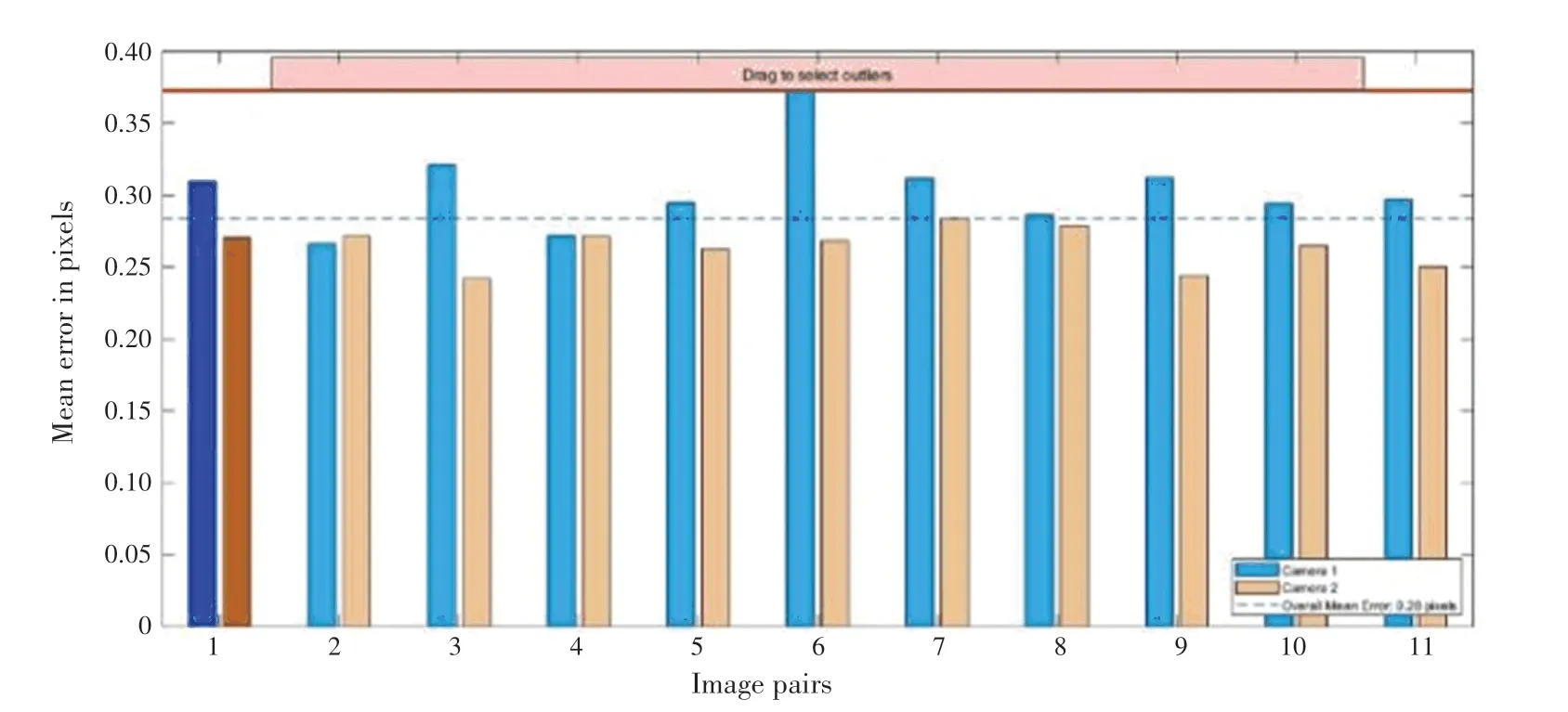
圖5 標定板重建的像素誤差Fig.5 Pixel errors in calibration plate reconstruction

3.2 儀表指針特征點的三維重建

首先采用灰度化、濾波、二值化、膨脹腐蝕等圖像預處理方法以及霍夫直線檢測方法，識別出指針式儀表左右視圖上指針的所在位置，并對其進行標注，其中一個視圖中儀表指針識別結果如圖6所示。

圖6 指針識別Fig.6 Pointer recognition

進一步地，通過利用標定獲得的相機內、外參數對左、右視圖進行畸變校正以及極線約束，使雙目相機所采集到的左、右視圖上的所有匹配點處于同一水平狀態，如圖7所示。其中，指針上標出的紅色圓點為指針與極線約束后提取的特征點，即左、右視圖中提取的指針匹配點。

圖7 校正后指針特征點的選取Fig.7 Selection of pointer feature points after correction

在獲得了2組匹配點之后，使用匹配點在左、右視圖中的二維圖像坐標，以及雙目相機標定得來的參數，通過三角形算法進行三維重建，以得到指針上2個特征點的空間三維坐標，在三維空間中顯示如圖8所示。分別以坐標，關系建立指針的空間函數，如式（5）、（6）所示：

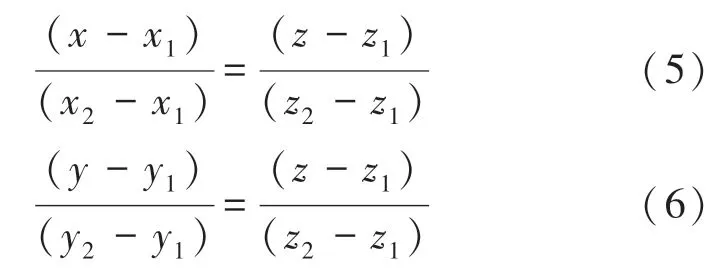
圖8中所顯示的橙色線段即為指針在空間中的重建，紅色圓點為指針重建后的特征點。

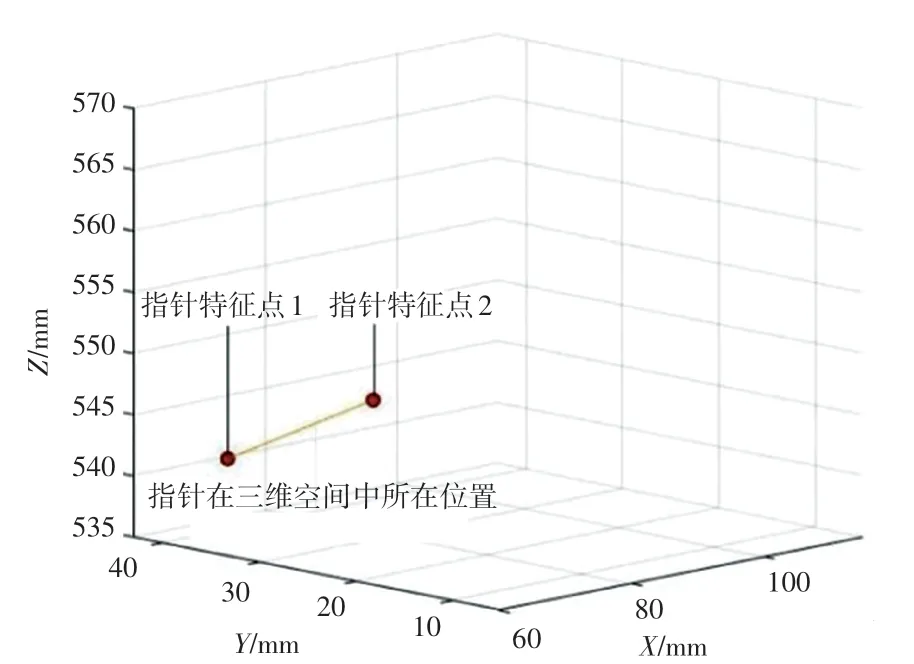
圖8 指針的三維重建Fig.8 3D reconstruction of the pointer

3.3 儀表表盤的三維重建

與指針的三維重建過程相似，在通過雙目相機標定消除畸變后，采用極線校正，使左、右視圖的表盤各特征點處于同一水平狀態。因儀表在左、右視圖中所占位置較小，在處理前先將儀表區域裁剪出來，接著再采用灰度化、去噪、二值化等圖像預處理操作提取出表盤刻度線骨架，最后采用極線約束，將左、右視圖中對應的表盤刻度線骨架與極線的交點作為一組表盤的匹配點，用此方法得到3組匹配點。如圖9所示。

圖9 校正后表盤特征點的選取Fig.9 Selection of dial feature points after calibration

利用雙目相機標定好的相機內、外參數，對得到的3組表盤匹配后的特征點進行三維重建，得到3個表盤特征點的空間三維坐標（，，）、（，，）、（，，），平面方程一般式如式（7）所示：

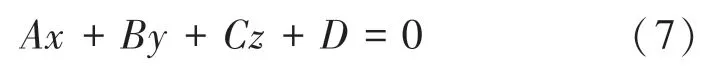
將前文求得3個三維空間坐標點代入公式（7）中可得三元一次方程組，解方程組求得參數、、，從而解析出平面方程。計算出對應的平面方程，并構建出表盤面在空間中的位置，如圖10所示。

圖10中黃色圓點為表盤重建后的特征點標點。

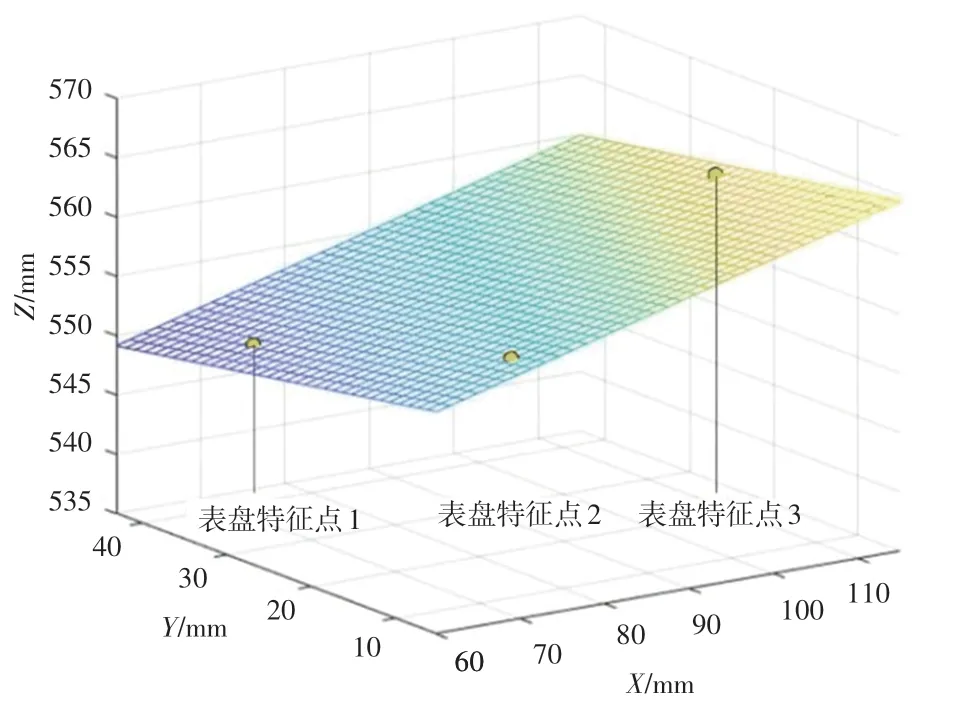
圖10 表盤的三維重建Fig.10 3D reconstruction of the dial

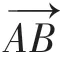
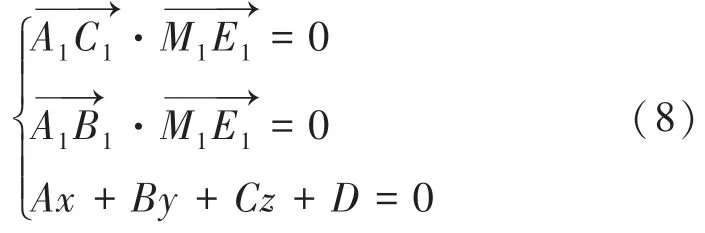
同理，可求出平面外另一點所對應的垂直投影坐標。

將重建后的指針目標點投影至構建的儀表盤平面，實現指針在儀表盤上的垂直投影，如圖11所示。

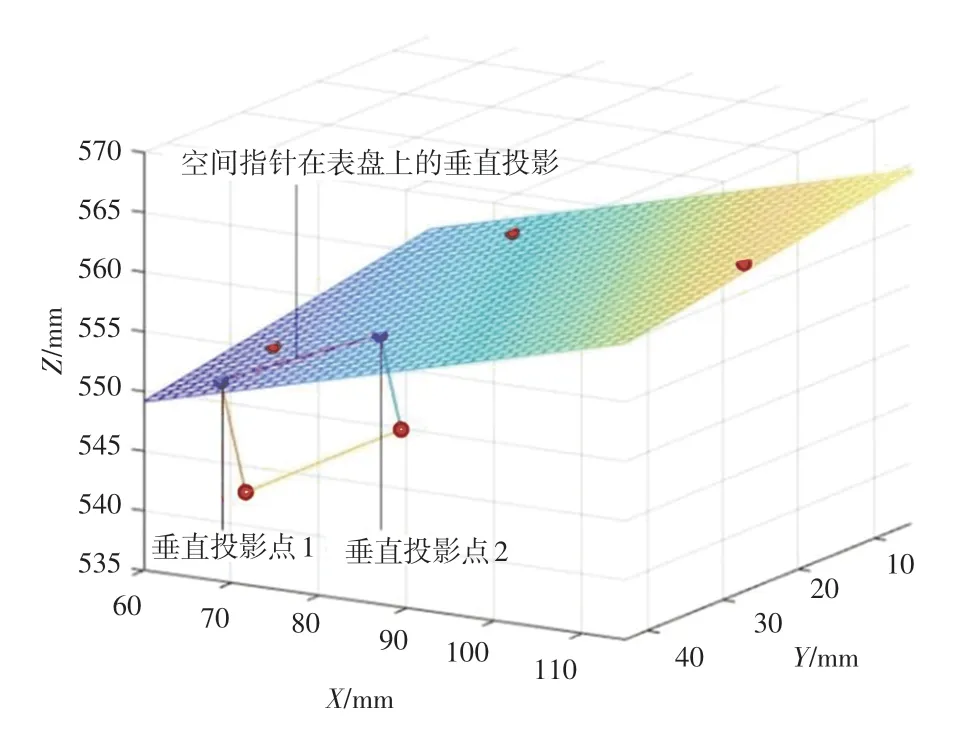
圖11 指針在表盤上的垂直投影Fig.11 Vertical projection of the hands on the dial

圖11中所顯示的紅色線段為空間中指針在表盤平面上的垂直投影，藍色圓點為空間中指針特征點在表盤平面上的垂直投影。

4 構建指針角度-儀表讀數模型

將重建后的指針垂直投影至儀表表盤，并將空間三維坐標系下的垂直投影坐標投影至二維平面坐標系。三維空間坐標投影至二維平面后，構建對應比例尺關系，這里通過區分不同象限與其所對應角度的關系計算出指針在每個象限的角度，0刻度時計算出的角度為最小角度，記為。0刻度所對應的量程為最小量程，記為；06刻度時計算出的角度為最大角度，記為。06刻度所對應的量程為最大量程，記為。以此為基礎構建指針角度與儀表讀數的比例尺，當前檢測角度記為，根據式（9）可計算出儀表讀數：

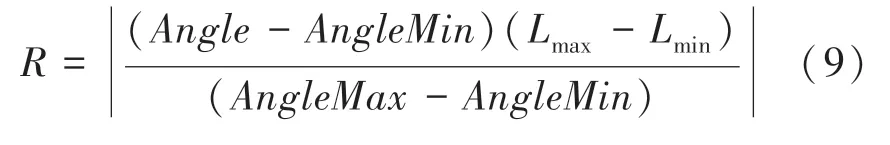
5 實驗結果與分析

通過實驗得到多組數據進行實驗如圖12所示。

圖12 多組實驗數據Fig.12 Multiple sets of experimental data

對比分析結果見表1，雙目視覺識別指針式儀表讀數是具備準確讀數效果。通過與左、右相機對比分析，可以發現，左、右相機單獨讀數至少存在一個相機的光軸中心未能對準指針儀表中心，從而引起讀數的誤差，這表示相機拍攝儀表存在傾斜角度時，會因為指針成像位置的改變而造成讀數誤差。經過雙目立體視覺對指針和表盤三維重建，獲取其深度信息后，可有效減小讀數的誤差，可有效地識別指針式儀表的讀數。

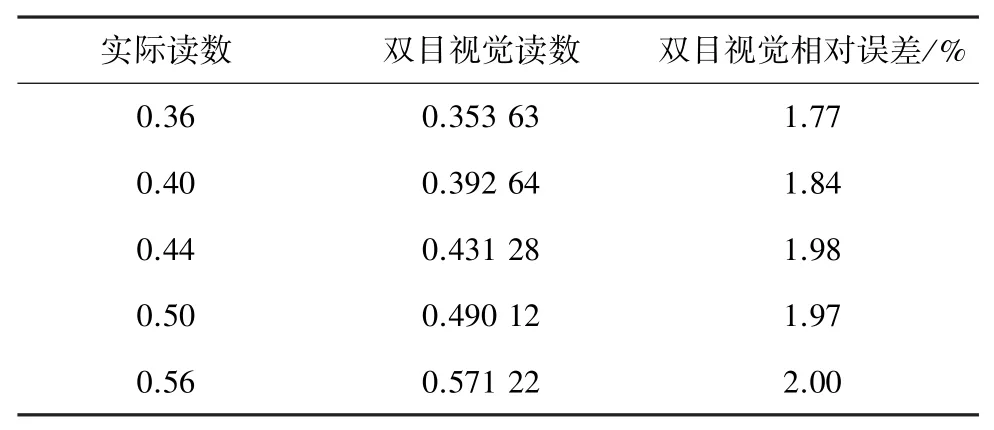
表1 讀數分析結果Tab.1 Results of analysis of readings

6 結束語

針對二維成像的儀表讀數受成像角度影響大的問題，設計了一種基于雙目視覺立體成像的指針儀表讀數識別，通過對雙目相機同步拍攝左、右視圖，并對左、右視圖進行預處理操作，尋找到左、右視圖中匹配的特征點進行三維重建，獲取其三維空間坐標，重建了指針及儀表后，將空間中的指針垂直投影至表盤平面，以此來消除由于視差所導致的讀數誤差，最后構建指針角度-讀數的比例尺關系計算讀數。經實驗證明，該方法具有較強的應用價值。

此外，指針式儀表的特征點選取及匹配直接影響到空間三維重建的精度，因此，該方案中特征點的選取以及匹配還存在進一步優化的空間。