基于B樣條曲線的無人駕駛車輛Informed RRT*算法研究

劉夢奇，王維強，田良宇

（武漢科技大學 汽車與交通工程學院，武漢 430065）

0 引 言

汽車產銷量的持續增長，使得城市交通控制任務面臨嚴峻形勢，而城市交通系統中有關交通擁堵、安全和環境污染等問題也不容小覷。隨著計算機云計算等新技術的快速普及，無人駕駛技術得到了重視與發展。無人駕駛車輛不僅可以降低事故的發生率，還可以提高汽車的出行效率。作為自動駕駛核心體系中的路徑規劃，一直都是無人駕駛領域的熱點與難點。

傳統的路徑規劃算法主要分為4類，分別是：基于圖搜索的算法，如A算法，D算法等；基于插值擬合的軌跡生成算法，如β樣條曲線等；以MPC為代表的用于局部路徑規劃的最優控制算法；基于采樣的算法，如PRM，RRT算法等。

其中，RRT是一種在完全已知的環境中通過采樣擴展搜索的算法，相較于其它的算法，最突出的優點就是快，而且其搜索過程不需要構建顯式的任務空間，計算簡單，且具有概率完備性。但同時也有著比較明顯的缺點，比如常常得不到最優解、規劃的路徑并不平滑等，因而后續提出了很多對RRT算法的改進策略。如，賀伊琳等人針對RRT算法盲目采樣的缺點，基于目標偏向策略，限制采樣區域，以一定的概率將目標點作為隨機點進行隨機樹擴張；針對RRT算法缺乏穩定性和收斂速度慢的問題，提出了一種改進的雙向搜索路徑規劃算法；Bormann等人提出了一種漸進最優版本的RRT改進算法RRT，該算法探索狀態空間的過程與RRT相似，但增加了父節點重新選擇和重新布線的步驟來保證最優性，且在可行解找到后，擴展過程并不停止，而是繼續不斷迭代找到更優的解，當迭代次數越來越多時，RRT會產生最優解或者幾乎接近最優的解。劉猛等人將RRT算法與三次曲線規劃相結合，通過三次曲線規劃使路徑趨向平滑，減少汽車自主泊車時的橫向移動。

為了解決RRT產生大的采樣空間且采樣時間長的問題，則隨即提出了Informed RRT算法。該算法在利用RRT找到初始解后，立即生成由起點、目標點、當前路徑長度決定的橢圓狀態空間區域，之后進行啟發式直接采樣，即把采樣范圍僅控制在這個能改善當前可行解的啟發式橢圓子集區域內，從而加速收斂到最優解。但Informed算法產生的路徑會產生明顯的拐角，使生成的路徑不平滑、質量差，本文擬進一步采用B樣條曲線函數來擬合生成的路徑點，從而生成曲率連續的平滑路徑。

1 相關算法與原理

1.1 RRT算法原理

RRT算法是由美國愛荷華州立大學的LaValle教授于1998年提出的，是基于概率采樣的運動規劃算法，能夠快速有效地搜索高維空間。算法運算流程如圖1所示。下面將闡釋分析RRT算法的核心操作。

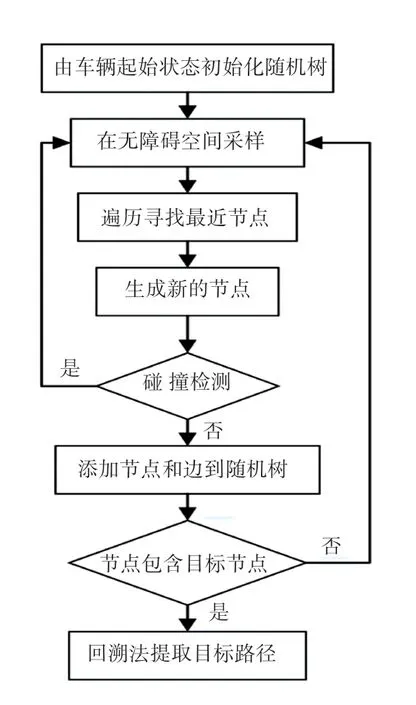
圖1 RRT算法流程圖Fig.1 Flow chart of RRT algorithm

（1）初始化。由于RRT需要知道完整的環境地圖，所以在初始化時要提供環境地圖，以進行后續的碰撞檢測，再將起點作為樹的根節點進行存儲。

（2）隨機采樣。確定起點和地圖后，在整個地圖中進行隨機采樣。

（3）樹節點擴展。尋找距離采樣點最近的樹中的節點，將其作為新擴展的節點的父節點，再以該父節點為基礎，向采樣點的方向延伸一定距離，將延伸后的節點作為新節點，并加入樹。

（4）終止條件。在樹節點擴展的方法基礎上，可以將擴展的新節點是終點作為終止條件。

1.2 RRT*算法原理

RRT算法的規劃結果通常不會最優，RRT就是針對RRT的規劃結果并非最優的局限性提出來的。在原始RRT的基礎上，RRT主要有2點改進，即：為新節點選擇代價最小的父節點、重布線。

RRT算法重選父節點和重布線示意圖如圖2所示。圖2中，首先，當采樣節點X加入節點樹后，以采樣點為圓心加一個小圓，考慮該圓圈內是否有更近的父節點使起點到該節點的距離最近；若存在更合適的父節點，就將其連接起來，并去除原來的連線，然后判斷圈內是否存在某種節點，該節點經過X節點到初始節點的代價比該節點到初始節點原路徑的代價小，若存在該類型節點，則將X節點作為該節點的父節點，并斷開該節點與原父節點的連接，最后重新進行連線。

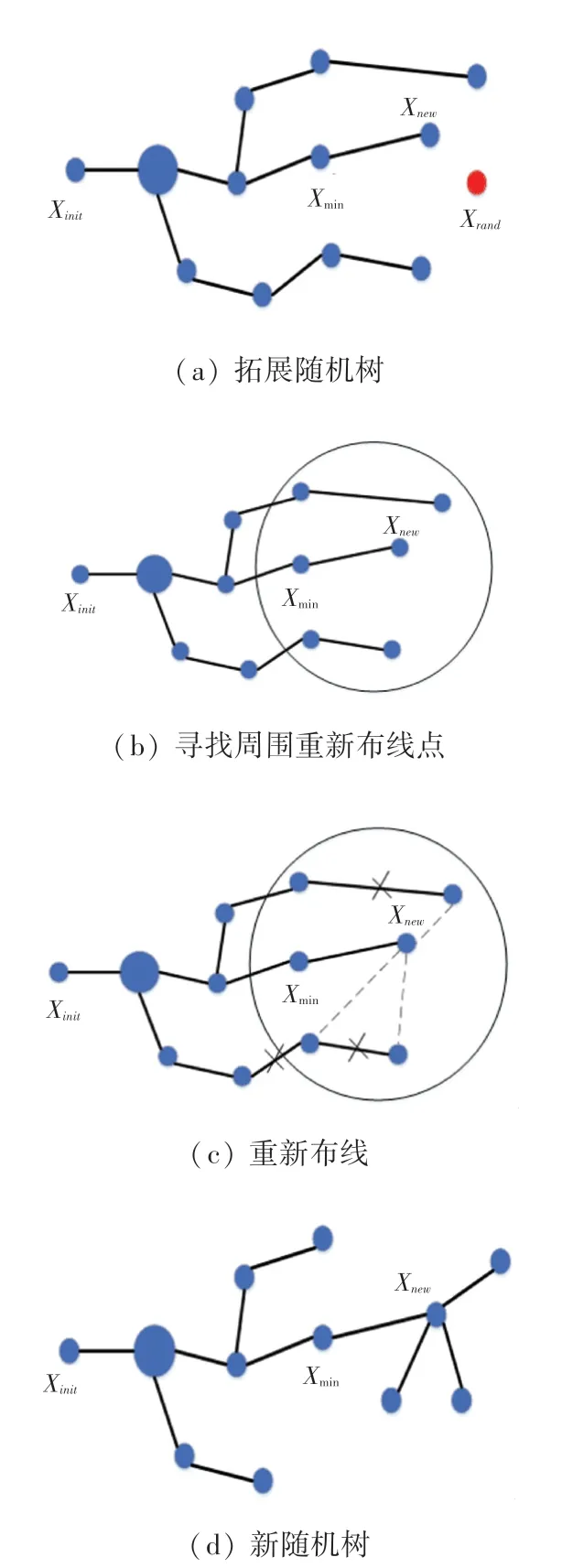
圖2 RRT*算法重選父節點和重布線示意圖Fig.2 Schematic diagram of RRT*algorithm for reselecting parent nodes and rewiring

1.3 Informed RRT*算法的原理

Informed RRT是在RRT的基礎上對采樣空間進行了優化，大大縮短了搜索時間。其偽代碼參見算法1。黑體部分為改進的地方，其中表示起點到終點的距離，C表示規劃路徑的長度，初始狀態下C為0。圖3為Informed RRT算法的采樣示意圖，將已經搜索到的最短路徑作為C，C作為橢圓的2個頂點2，作為橢圓的2個焦點，將采樣空間限制在橢圓內，以此來構建橢圓，如圖4所示。隨著路徑長度的不斷縮短，逐漸縮小該橢圓形區域。

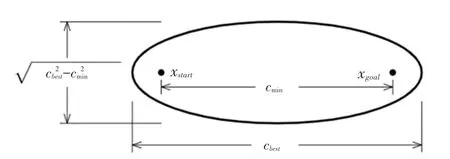
圖3 Informed RRT*采樣示意圖Fig.3 Schematic diagram of Informed RRT*sampling

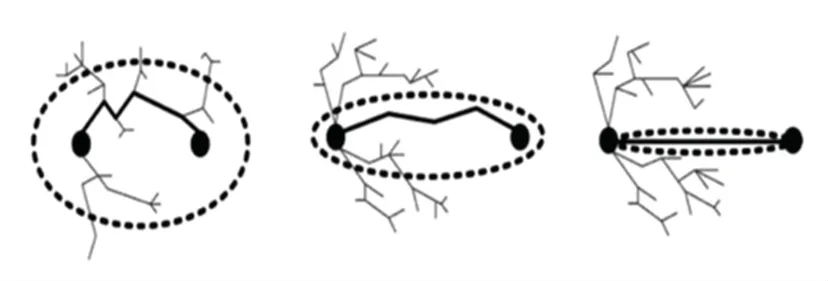
圖4 Informed RRT*搜索過程示意圖Fig.4 Schematic diagram of the Informed RRT*search process

Informed RRT(X，X)

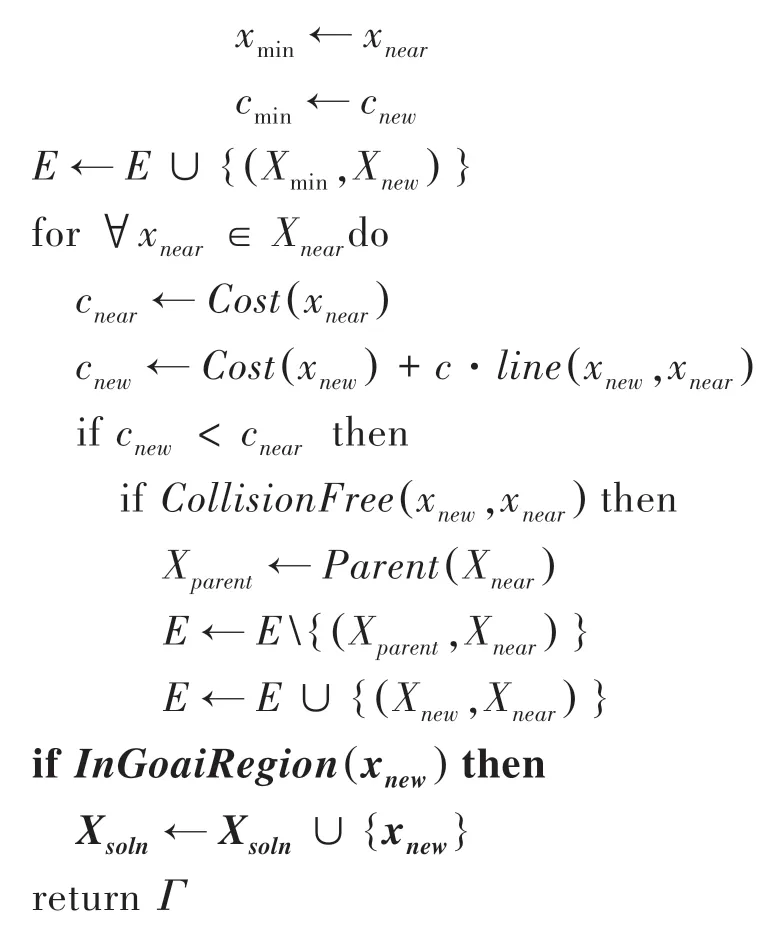
2 B樣條曲線擬合路徑點

用B樣條規劃路徑可以滿足規劃路徑時對局部路徑進行修改而不改變整個路徑形狀的要求，本文正是應用B樣條曲線的這些優點來完成路徑點的后期擬合，以生成光滑路徑。

設一共有1個控制點，這些控制點用于定義樣條曲線的走向、界限范圍，則階B樣條曲線的定義為：

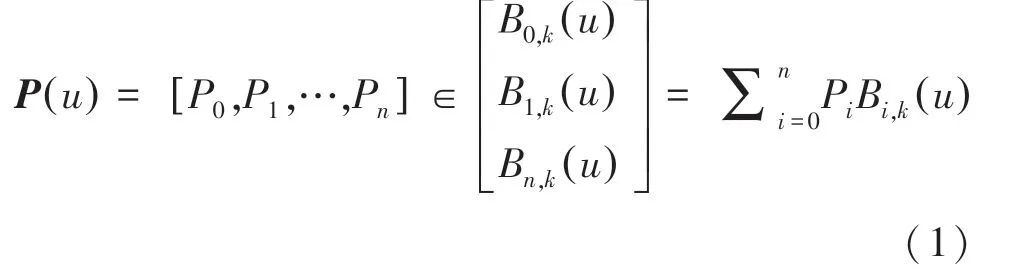
其中，B（）是第個階B樣條基函數，與控制點相對應，≥1；是自變量，基函數有以下推導式：

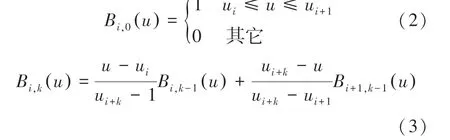
一個非減的實數序列［，…，］稱為節點向量，B樣條基函數B（）在區間［u，u］之外為0，對所有，和都為非負。

一般來說，B樣條曲線分為均勻B樣條曲線和準均勻B樣條曲線，本文選擇準均勻B樣條曲線，因為這是兩端節點具有重復度、中間節點非遞減的序列，故而有著更為廣泛的應用。還需指出的是，B樣條曲線公式中的值代表曲線的平滑度，值越大，曲線的平滑度越高，但計算復雜度也越高；值過小，曲線的平滑度就差。為兼顧無人車軌跡的平滑度與計算復雜度，本文最終選擇三階B樣條曲線，即3，將起始點和目標點都設置為3重節點。

3 仿真結果與分析

為了驗證算法改進的有效性，擬基于Matlab軟件進行路徑規劃仿真實驗。實驗仿真環境為800 m*800 m的矩形區域，設置起始坐標（0，0），目標點（700，700），在Matlab中對RRT、RRT、Informed RRT、基于B樣條優化的Informed RRT四種算法進行仿真。仿真實驗對比的評價指標包括平均采樣的數目、平均規劃時間和平均路徑長度等。算法生成隨機樹上的采樣節點越少，規劃時間越短，則說明算法規劃路徑的效率越高，規劃的優越性更好。

3.1 RRT、RRT*、Informed RRT*三種算法的仿真分析

圖5為RRT、RRT、Informed RRT三種算法在障礙物環境下的仿真實驗規劃結果對比圖。

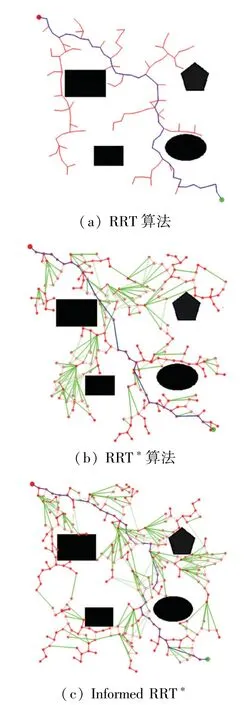
圖5 3種算法仿真結果實驗圖Fig.5 Experimental diagram of simulation results of three algorithms

3種算法50次實驗的平均采樣時間、平均采樣長度、平均采樣節點數的數據對比見表1。

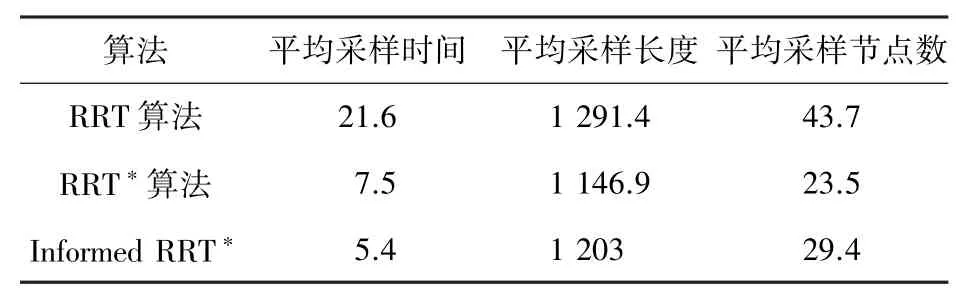
表1 算法對比指標數據Tab.1 Indicator data comparison of three algorithms

由表1可知，基本RRT算法的平均采樣時間，平均采樣長度和平均采樣節點較大，RRT算法和Informed RRT算法在各項評價指標上則有較大的改進，特別是在采樣時間和采樣節點上均有顯著的下降。與RRT算法相比，Informed RRT算法的大多數分支集中在起始點和終止點的空間，反復實驗過程中，最終路徑并無太大變化，而RRT樹支基本遍布整個空間，每次運行生成的路徑都不相似，隨機性較大。同時，其采樣時間提高了大約28%，采樣長度和平均采樣節點并無太大變化。

3.2 基于B樣條曲線的優化仿真

進行B樣條曲線的優化仿真，圖6為基礎的Informed RRT仿真結果圖，圖7為加入B樣條曲線平滑后的路徑對比，圖8為局部優化對比圖，圖9為基于三次B樣條曲線軌跡優化后路徑的曲率變化圖。

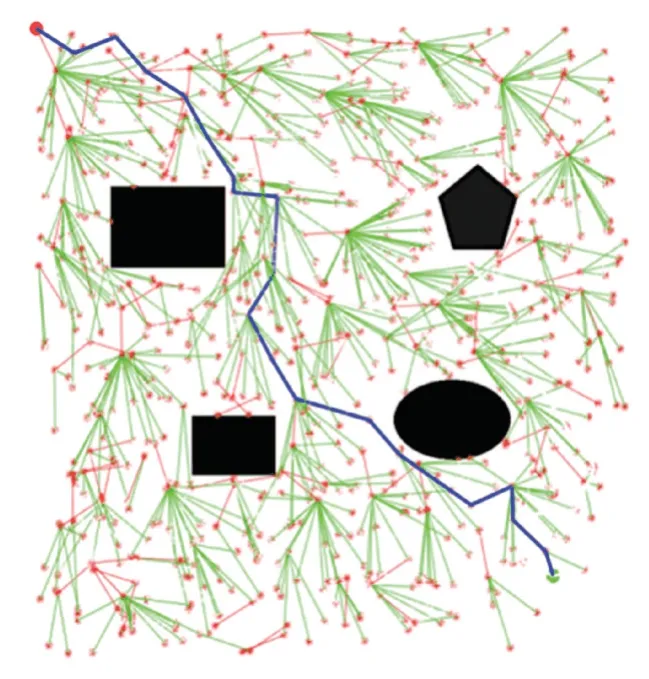
圖6 Informed RRT*仿真結果Fig.6 Simulation results graph of Informed RRT*

圖7 B-Informed RRT*平滑路徑對比圖Fig.7 Comparison of B-Informed RRT*smooth path

圖8 局部優化圖Fig.8 Local optimization diagram

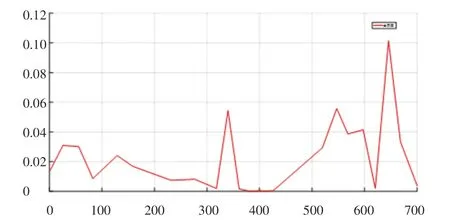
圖9 基于三次B樣條曲線的軌跡優化曲率變化圖Fig.9 Trajectory optimization curvature change diagram based on cubic B-spline curve

由圖6～圖9可知，加入了B樣條曲線擬合后的路徑平滑性更高，經B樣條曲線擬合后，所得曲線能夠沿給定趨勢變化，剔除了控制曲線中的尖點及曲率半徑較小處的點，曲線的平滑度有了一定程度的提高。其中，三次B樣條擬合曲線的曲率半徑更小，尖點處的過渡更為平滑，從車輛最大轉彎半徑求得允許最大曲率為0.14，優化路徑的最大曲率小于0.12，經過對比可以發現B樣條曲線優化后的曲率連續且滿足車輛的曲率范圍，適用于車輛規劃軌跡。

4 結束語

綜上所述，通過對比RRT、RRT、Informed RRT算法，本文提出的B-Informed RRT算法生成的路徑平均曲率降低，路徑平滑點增加，同時采樣時間和采樣節點的降低，使得軌跡的生成速率有了較大的提升，從而提高了軌跡規劃的實時性，能夠在一定程度上滿足車輛在高速行駛時的軌跡規劃要求；而且加入了三次B樣條曲線，在無人駕駛汽車軌跡規劃中具有較強的實用性。