基于全局帕德逼近的米塔-列夫勒函數及其導數的數值算法

方宇孟，袁 曉，謝雨婧

（四川大學 電子信息學院，成都 610065）

0 引 言

在經典的整數階微分方程理論中，指數函數e（∈?）起著非常重要的作用，且是微分方程

的解：（）e。

復變量（i）的整函數—解析指數函數e的冪級數展開為：

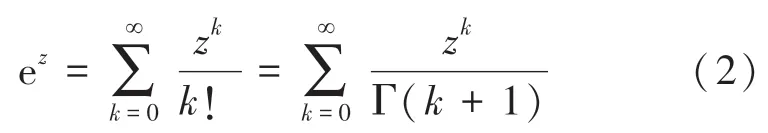
e的任意有限階導數等于自身，這一特性對傅里葉變換、拉普拉斯變換和變換意義重大。

1903年，米塔-列夫勒提出單參數米塔-列夫勒函數：

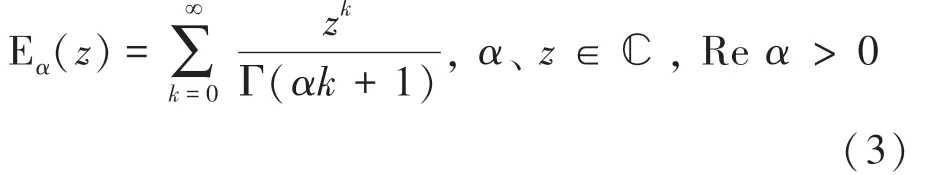
其中，E（）是指數函數的單參量廣義化結果。

1905年，Wiman提出雙參數米塔-列夫勒函數：

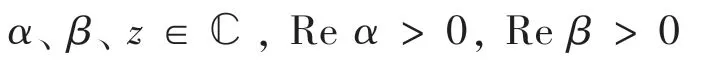
顯然有：EE。

1971年，Prabhakar提出三參數米塔-列夫勒函數：

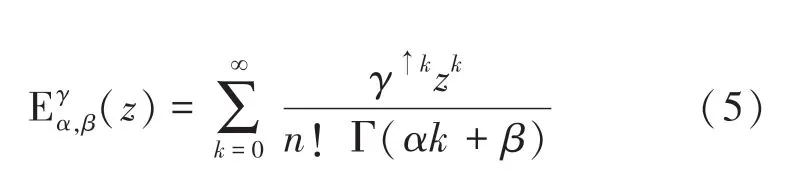
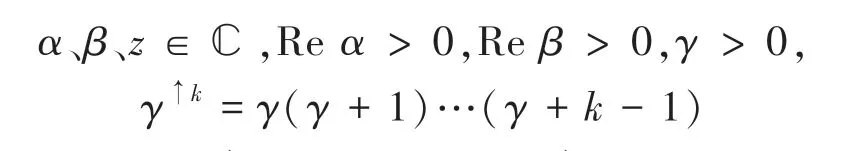
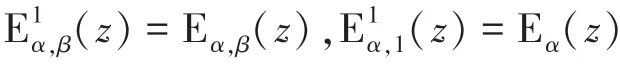
米塔-列夫勒函數在分數階系統中的重要性如同指數函數在整數階系統中的重要性。E（）稱為分數微積分的女王函數（the Queen Function of Fractional Calculus）。米塔-列夫勒函數類可用于表示分數階微積分方程的解，比如：第二類阿貝爾積分方程，含有黎曼-劉維爾分數導數的微分方程等，還可應用于許多現代分數階模型，比如：神經網絡中的信息處理、聚合物網絡中的黏彈性、分子輸運、熱傳導、信號處理和反常擴散。

米塔-列夫勒函數廣泛應用在各種研究領域與工程應用之中，因此有必要研究米塔-列夫勒函數的快速有效高精度算法。2002年，Gorenflo等人提出分區算法，采用泰勒級數、積分表達和漸進級數三種方法來計算米塔-列夫勒函數，但算法存在計算錯誤。2015年，Garrappa等人基于米塔-列夫勒函數的拉普拉斯變換，提出最優拋物線圍線算法。2018年，Garrappa等人在文獻［17］中研究了帶矩陣參數的米塔-列夫勒函數的數值計算。2020年，Saenko提出一種新的積分算法，將米塔-列夫勒函數的積分表示成實部和虛部的和且每部分只依賴實變量和實參數，但算法存在一定局限性。

除了以上提到的算法，研究者們還將帕德逼近法應用于米塔-列夫勒函數的數值計算。帕德逼近（Padéapproximation）是法國數學家亨利·帕德提出的有理多項式近似法，往往比截斷的泰勒級數準確。2007年，Starovoitov等人利用帕德逼近法研究了米塔-列夫勒函數在｛≤1｝范圍內的計算。文獻［20］和文獻［21］基于帕德逼近法研究了米塔-列夫勒函數E（-x）（0）的上下邊界。

2003年，Winitzki在帕德逼近的基礎上提出全局帕德逼近（global Padéapproximation），構造了超越函數的一致逼近。2005年，Diethelm等人提供了米塔-列夫勒函數E（-x）（01）的有理逼近系數表，在{∈［01，15］}范圍內具有良好的計算精度。2011年，Atkinson等人利用全局帕德逼近法實現米塔-列夫勒函數E（）在{01，0}范圍內的二階逼近，但二階逼近的效果差，為了進一步提高計算精度，需要擴展到更高階逼近。

在前人研究基礎上，本文將全局帕德逼近法應用于雙參數米塔-列夫勒函數E（）及其任意階導數的數值計算，實現了10階逼近，計算精度可達1×10%。經理論分析和仿真實驗，證明了該算法的運算有效性和可行性。

1 米塔-列夫勒函數的基本性質

米塔-列夫勒函數最主要的性質有4種：積分、微分、漸進、拉普拉斯變換。這些性質不僅有助于求解分數階微積分方程，而且在實際的工程應用中具有重要意義，比如：Bagley-Torvik方程的數值求解，分數階被控系統和分數階PD控制器系統中表示單位階躍響應，電介質的分數階松弛方程的求解等。

1.1 米塔-列夫勒函數的積分

對雙參數米塔-列夫勒函數（4）逐項積分得：

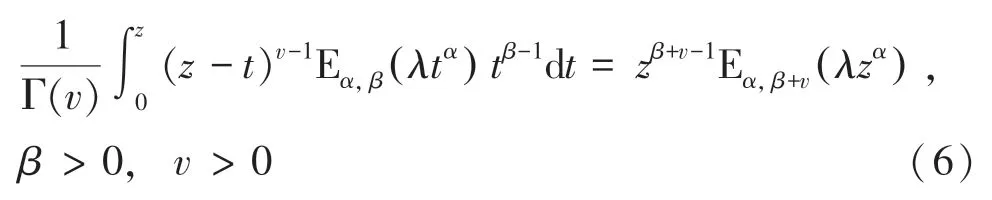
其中，當＝1時，得到式（6）的一個特例：

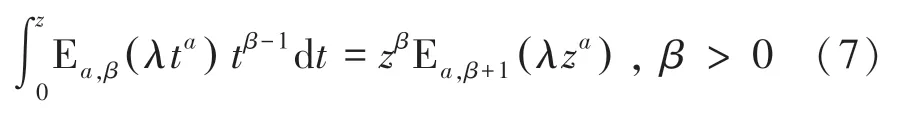
Erdélyi等人和D?rba?yan等人研究了米塔-列夫勒函數沿漢克爾環的反常積分形式，得到定理1。

設02且∈?，則對任意0與，滿足π2≤min｛π，π｝時，有：

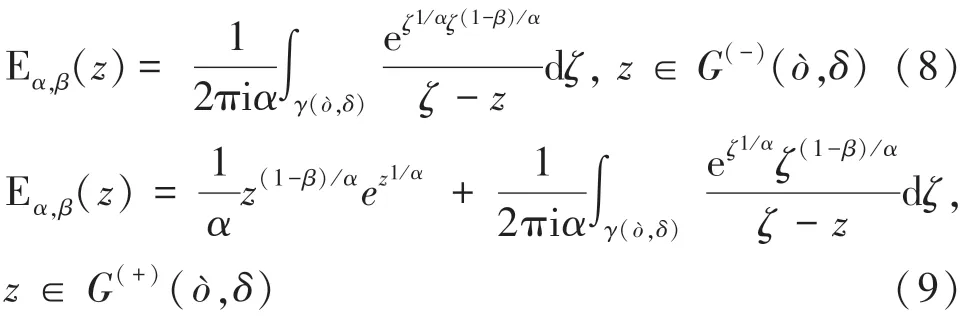
其中，積分圍線（，）如圖1所示，由2條射線S（arg，≥）和S（arg，≥）以及一個圓弧C（0，）（，≤arg≤）組成。積分圍線左側區域是（，），右側區域是（，）。表示圓弧G的半徑，表示積分變量的角度。

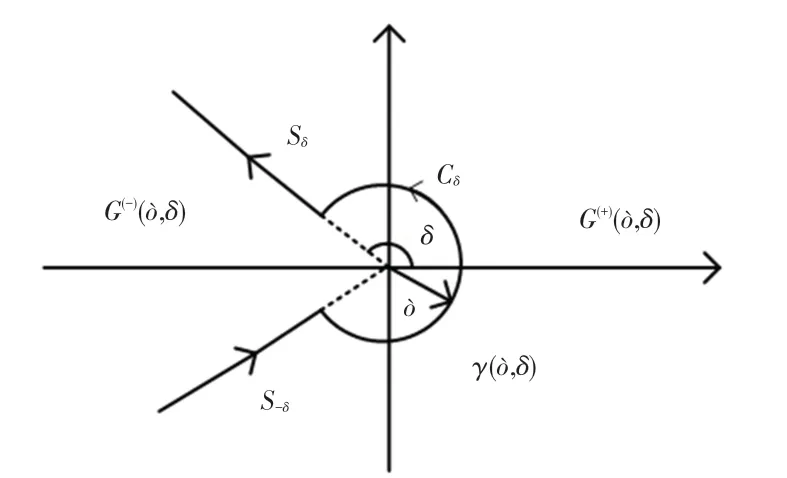
圖1 積分圍線γ（ò，δ）［14］Fig.1 Integral contourγ（ò，δ）［14］

1.2 米塔-列夫勒函數的微分

對雙參數米塔-列夫勒函數E（）逐次求導可得階導數公式：

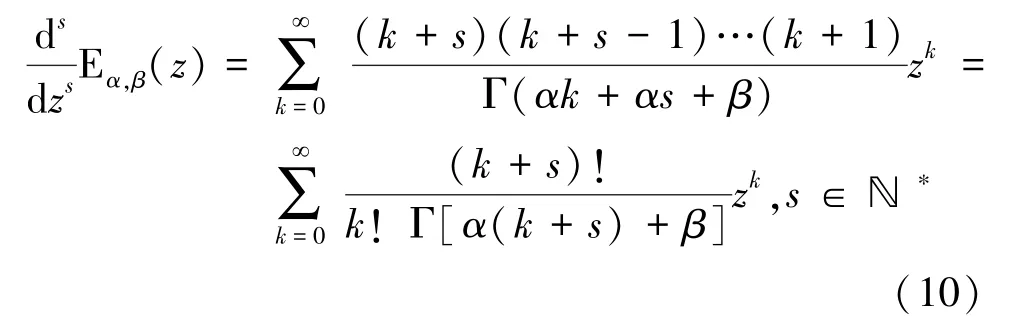
另外，文獻［5］中給出階導數公式：

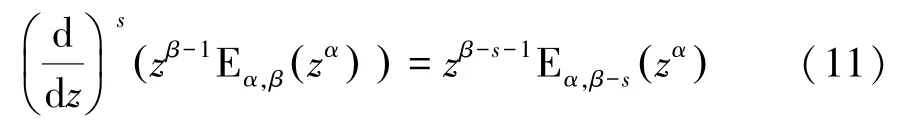
1.3 米塔-列夫勒函數的漸進展開

利用式（8）和式（9）的積分表達得到米塔-列夫勒函數在復平面上的漸進表達。

對于02、∈?、∈?，當argmin｛π，π｝時，有漸進展開式：

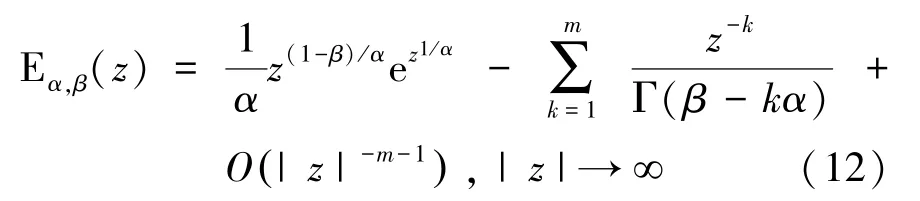
當01，πargπ時，有漸進展開式：

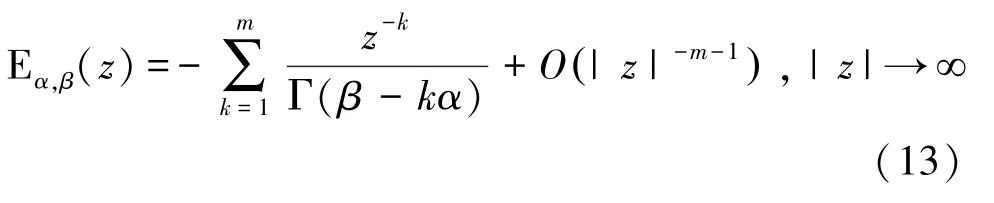
1.4 米塔-列夫勒函數的拉普拉斯變換

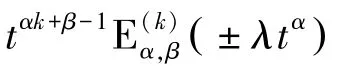
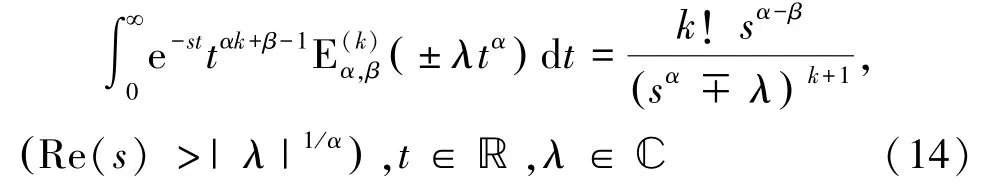
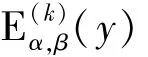
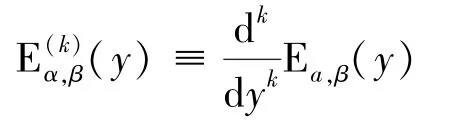
2 米塔-列夫勒函數的數值算法

2.1 分區算法

Gorenflo等人提出分區算法，用泰勒級數、積分表達和漸進級數計算復平面上不同區域的米塔-列夫勒函數。Seybold等人在Gorenflo等人的基礎上做了改進，消除了變量靠近積分圍線時的不穩定現象。

對于0、∈?，分區算法能夠計算復平面上任意米塔-列夫勒函數E（）的值。對復平面上的不同取值，采用不同的數值計算方法，以獲得最佳的穩定性和精度。基本思路是：當0≤1、∈?時，≤則用泰勒級數（式（4））計算；≥則用漸進級數（式（17）和式（18））計算；則用積分表達（式（8）和式（9））計算。其中，表示采用泰勒級數方法的區域半徑上限值，表示采用漸進級數方法的區域半徑下限值。當1時，用遞歸公式將其轉為0≤1的情形再計算：

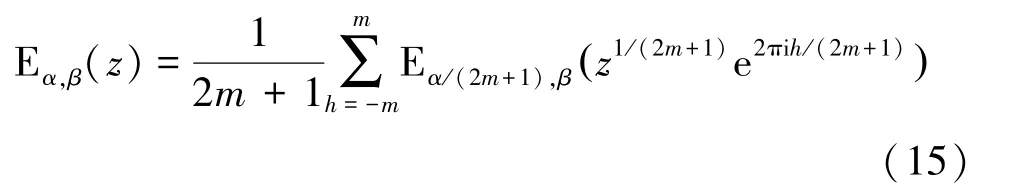
其中，∈?，∈?；［（1）2］1；［］為不超過的最大整數。

然而，分區算法存在一定缺陷。Popolizio等人指出分區算法存在計算錯誤。Saenko證明了定理1有誤，當∈（，）時，積分表達式正確；當∈（，）時，積分表達式錯誤。指出分區算法因使用了定理1導致∈（，）產生計算錯誤。

2.2 最優拋物線圍線算法

Garrappa等人提出最優拋物線圍線算法，在復平面上選擇計算量和誤差都最小的區域，對米塔-列夫勒函數進行拉普拉斯反演計算。適用范圍：0，∈?，∈?。核心計算公式為：

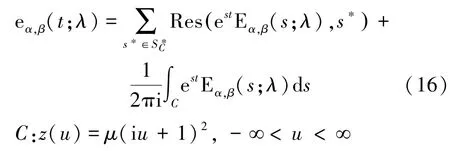
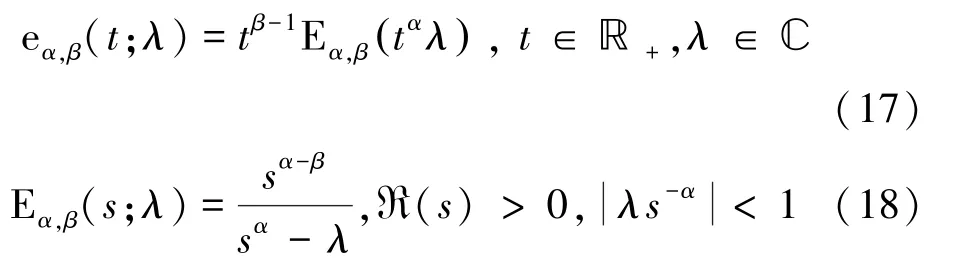
2.3 全局帕德逼近算法

2.3.1 全局帕德逼近

帕德逼近是從冪級數出發獲得有理逼近的一種簡潔且有效的方法。其基本思想是對一個給定形式的冪級數構造一個有理函數，使該有理函數的泰勒展開盡可能與原來的冪級數吻合。這種方法克服了用多項式逼近大擾度函數效果不理想以及用冪級數（如泰勒級數）逼近函數收斂性太差等缺點。

設函數（）∈［，］，1，如果有理函數R（）可展開為：

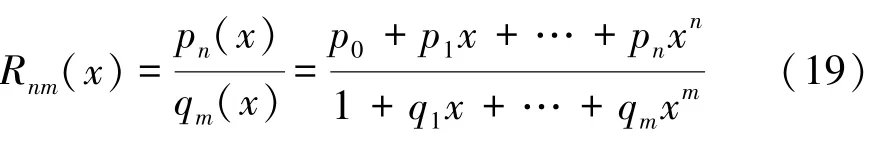
其中，p（）和q（）互質，且滿足條件：

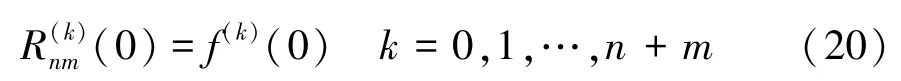
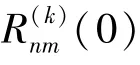
Winitzki對式（19）進行改進，提出全局帕德逼近形式：

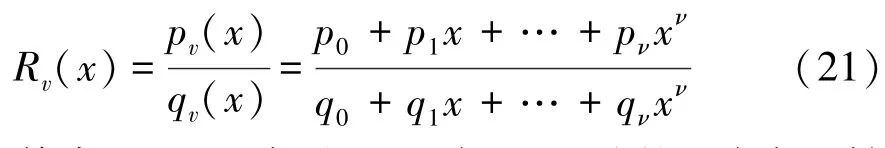
其中，R（）表示（）在0處的階全局帕德逼近。

2.3.2 米塔-列夫勒函數的全局帕德逼近

Winitzki利用全局帕德逼近法實現了橢圓函數、誤差函數、貝塞爾函數和艾里函數的有理逼近。全局帕德逼近法主要是利用初等函數的泰勒級數和超越函數的漸近級數實現計算。當｛0≤1，≥｝時，米塔-列夫勒函數E（）在［0，∞）上是單調且有限的，有E（∞）0。根據Winitzki的思想，可將全局帕德逼近法擴展到雙參數米塔-列夫勒函數E（）(≥0)的數值計算之中，分2種情況計算：｛0≤1，｝和｛01｝。

（1）情況一：｛0≤1，｝

根據雙參數米塔-列夫勒函數定義式（4）得Γ（）E（）的泰勒級數和漸進級數：

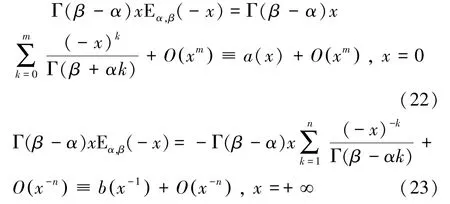
其中，加權項Γ（）保證漸近級數（23）的第一項系數為1。

對式（22）和式（23）取全局帕德近似：

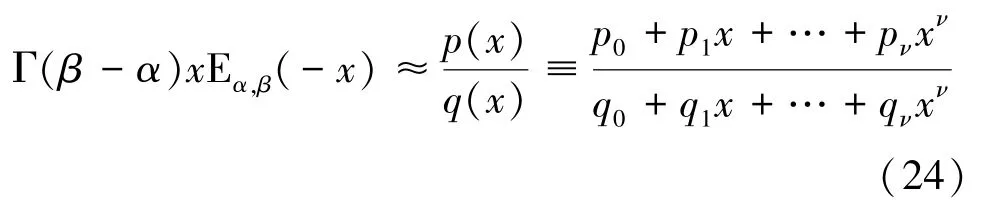
其中，∈?，表示全局帕德逼近的階數。而當＝∞時，式（24）右邊多項式的值為p／q，且可令p＝q＝1。未知系數p和q（0，1，…，1）可由線性方程組求出：

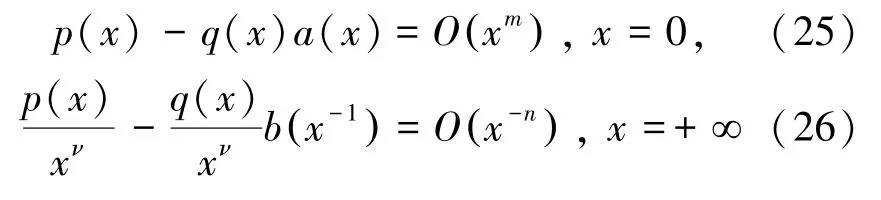
其中，當為奇數時，該非齊次線性方程組存在唯一解。當≈時，式（24）的近似效果最好。

根據文獻［34］提及的米塔-列夫勒函數的2階逼近多項式，對式（22）和式（23）截斷為1階和2階，令式（24）中2，得到：

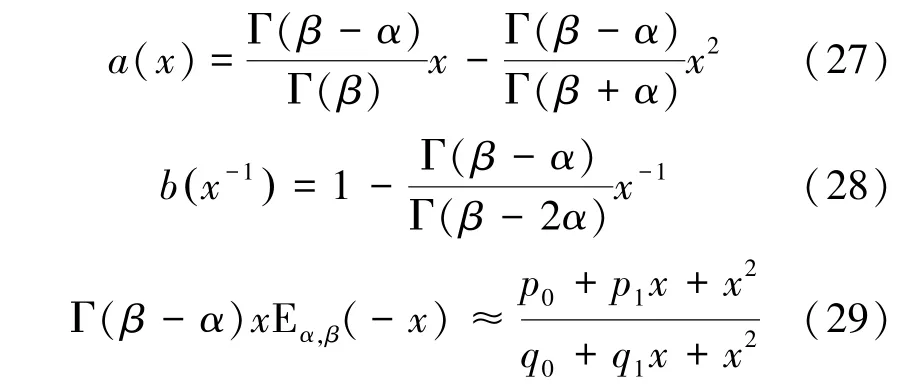
將式（27）～式（29）代入式（25）和（26）中，解出系數：

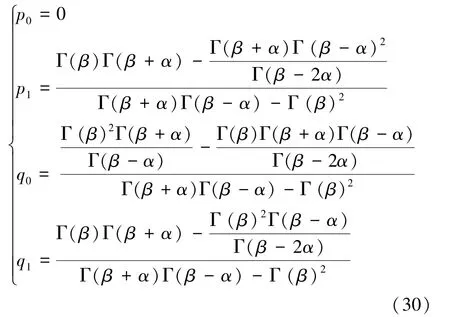
將式（30）代入式（29）中得到E（）的2階全局帕德逼近式：

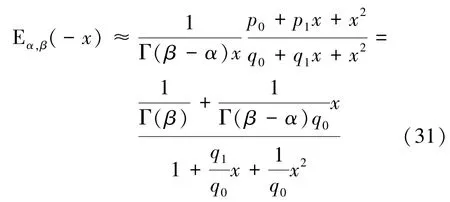
同理，若要計算E（）的階逼近，對式（22）和式（23）截斷為1階和階，得：

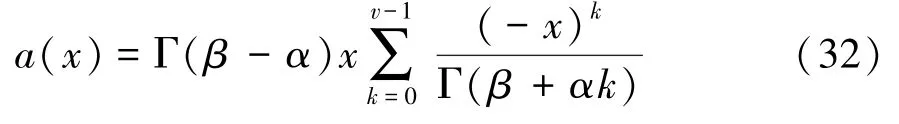
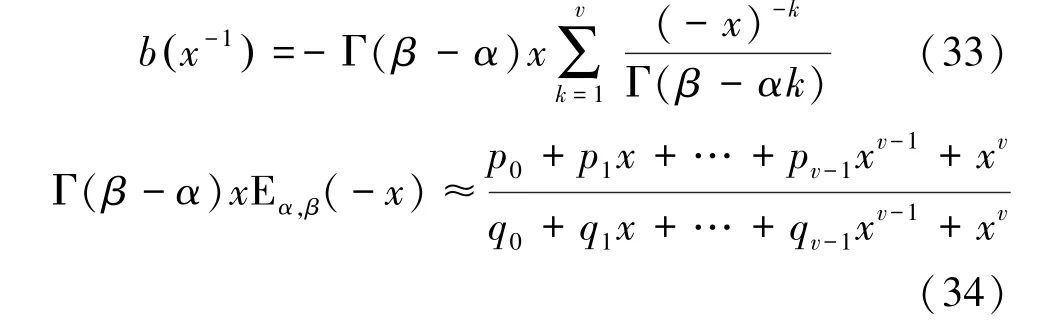
將式（32）～式（34）代入式（25）和式（26）中，求解式（34）中的系數p和q（0，1，…，1）。但隨著式（34）中等號右邊的多項式階數的增大，系數p和q的表達式中的Γ代數項也會增多。當階數7時，系數p和q的表達式中的Γ代數項超過1 000個。當式（32）～式（34）中多項式階數較大，難以手算求解，可借助Matlab軟件中的（）函數求解代數方程，得到系數p和q的表達式。

系數p和q的表達式只跟參數和有關，因此可根據參數和的取值，預先計算系數p和q的值并存入矩陣中，以優化精度、計算時間和系統內存。

經過Matlab軟件求解可知，僅0，～p（2）的表達式太過復雜不便于表示，由式（34）得E（）的階全局帕德逼近式：

（2）情況二：｛01｝

當時，米塔-列夫勒函數E（）有泰勒級數和漸進級數：

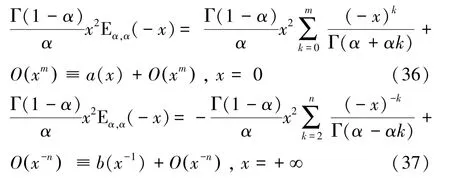
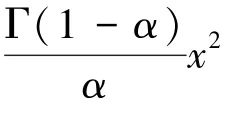
基于情況一的方法，解出情況二時E（）的2階全局帕德逼近式：

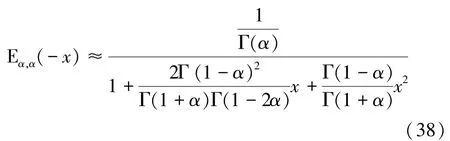
經Matlab軟件求解可知，僅0，得E（）的階全局帕德逼近式：

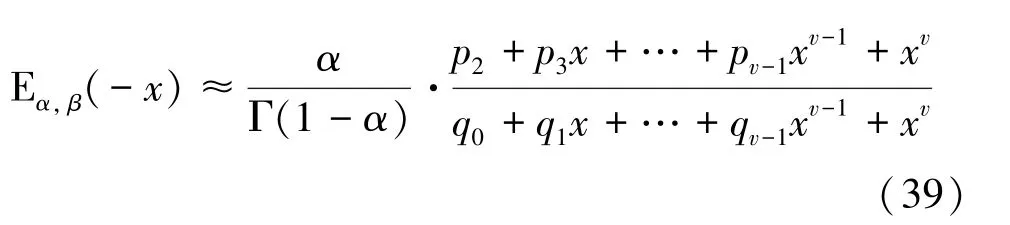
2.4 仿真結果及分析

為研究全局帕德逼近算法對米塔-列夫勒函數的逼近效果，需要考慮的影響因素有：逼近階數和參數。可將全局帕德逼近算法、分區算法和最優拋物線圍線算法做比較，綜合分析全局帕德逼近算法的逼近性能。

相對誤差函數的數學定義為：

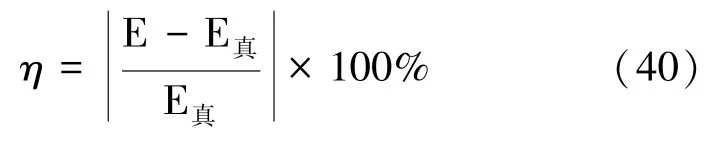
米塔-列夫勒函數E（）和E（）的解析為：

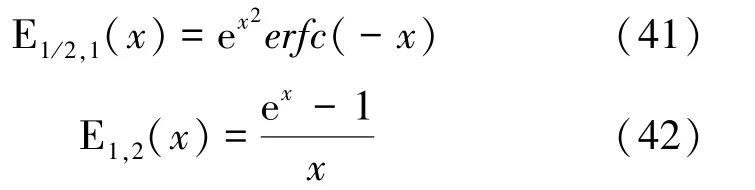
其中，誤差函數（）：

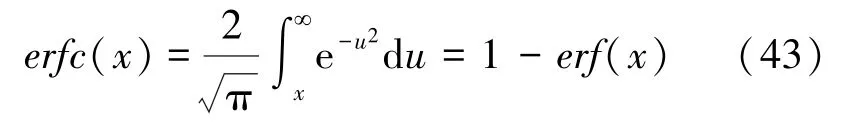
在此基礎上，擬對仿真結果進行剖析分述如下。

（1）分區算法、最優拋物線圍線算法和全局帕德逼近算法的比較。這里利用分區算法、最優拋物線圍線算法、全局帕德逼近算法和解析式（42）繪制米塔-列夫勒函數E（）曲線，并繪制3種算法與解析解之間的相對誤差曲線，如圖2所示。觀察到，最優拋物線圍線算法在整個區間內的計算精度最好，誤差穩定在110數量級。分區算法的誤差在區間（10，15）內急劇增大，最高達530.6%，在其他區間的計算精度很好，甚至在區間（14，1 000）內的相對誤差為0。全局帕德逼近算法的10階逼近的最大誤差為110610，而在區間（150，1 000）內的誤差穩定在110數量級。

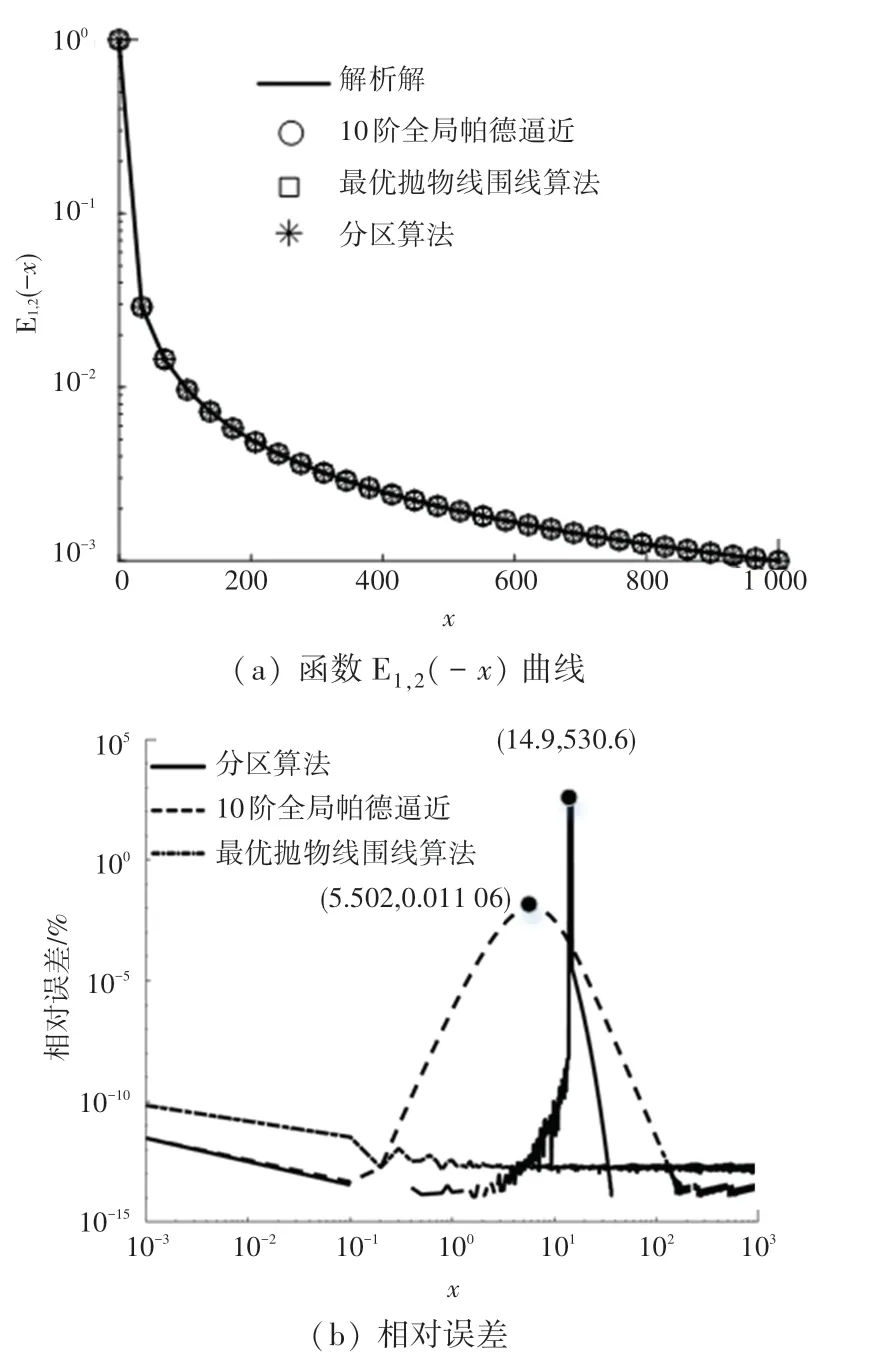
圖2 α＝1，β＝2，比較分區算法、最優拋物線圍線算法和全局帕德逼近算法Fig.2 Comparing the partitioning algorithm，the optimal parabolic contour algorithm and the global Padé approximation algorithm forα＝1，β＝2

文獻［31］提到分區算法因使用了錯誤的積分表達導致∈（，）時產生計算錯誤，因此在區間（10，15）內的誤差非常大。由此看出，分區算法的計算準確性不如全局帕德逼近算法和最優拋物線圍線算法。最優拋物線圍線算法的計算精度高且穩定，可用于下文驗證全局帕德逼近算法的逼近性能。

（2）全局帕德逼近算法的逼近性能。為探究逼近階數對逼近效果的影響，可繪制不同階數下全局帕德逼近的相對誤差曲線，如圖3所示。當｛01｝時，將全局帕德逼近算法和最優拋物線圍線算法的計算結果相比較，如圖3（a）所示。當｛0≤1，｝時，將全局帕德逼近算法和解析式（41）～（42）的計算結果相比較，如圖3（b）和圖3（c）所示。圖3展示了逼近階數2，4，6，8，10時的全局帕德逼近的相對誤差。

為探究對逼近效果的影響，固定的值，繪制在不同取值時的相對誤差曲線，如圖4所示。其中，縱坐標表示全局帕德逼近算法和最優拋物線圍線算法之間的相對誤差。

當逼近階數2時，難以手算求解系數p和q，可借助Matlab軟件求解。當05、1時，對應的10階全局帕德逼近系數p和q（0，1，…，9）的值見表1和表2。

表1 系數pi（i＝0，1，…，9）的值（α＝0.5，β＝1，v＝10）Tab.1 The value of the coefficient pi（i＝0，1，…，9）（α＝0.5，β＝1，v＝10）

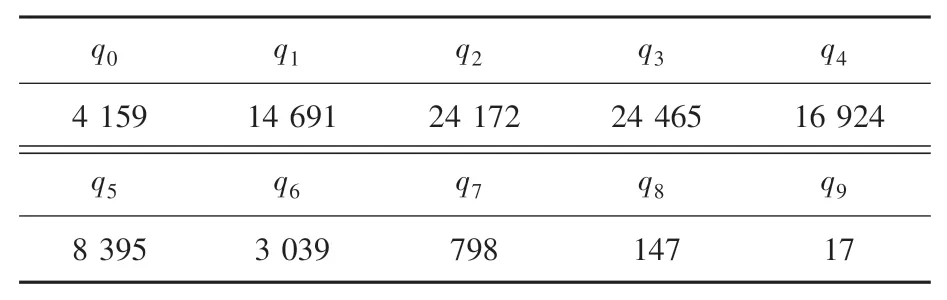
表2 系數qi（i＝0，1，…，9）的值（α＝0.5，β＝1，v＝10）Tab.2 The value of the coefficient qi（i＝0，1，…，9）（α＝0.5，β＝1，v＝10）

觀察圖3和圖4，可得結論：

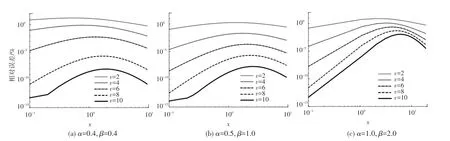
圖3 v對逼近效果的影響Fig.3 The effect of v on the approximation

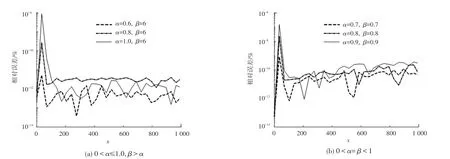
圖4 α對逼近效果的影響Fig.4 The effect ofαon the approximation

（1）全局帕德逼近算法能在任意逼近階數下計算米塔-列夫勒函數E（），逼近階數越高，誤差越小，逼近效果越好。當逼近階數10時，已提供了足夠的計算精度，和最優拋物線圍線算法相當，計算精度可達110。

（2）當的值固定時，的值越接近1，在區間（0，200）內的誤差越大且存在一個最大誤差，而誤差在區間（200，∞）內穩定在低水平。

（3）當取值很小或很大時，全局帕德逼近算法的優勢尤其明顯，計算精度很高。取中間值時存在最大誤差，可提高逼近階數來降低誤差。

3 米塔-列夫勒函數導數的全局帕德逼近

3.1 任意階導數的全局帕德逼近

將全局帕德逼近算法擴展到米塔-列夫勒函數任意階導數dE（）d（）（0，∈?）的數值計算，與2.3節方法相同，分2種情況：｛0≤1，｝和｛01｝。為了便于計算，取，則任意階導數表示為：

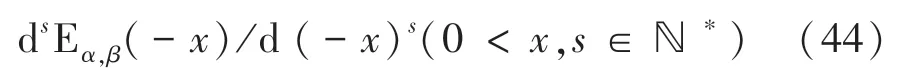
表3總結了雙參數米塔-列夫勒函數任意階導數的全局帕德逼近，列出了參數適用范圍、核心計算公式（泰勒級數和漸進級數）以及階全局帕德逼近式。其中，表示米塔列夫勒函數的導數階數，表示全局帕德逼近算法的逼近階數，p和q表示全局帕德逼近式的系數。得到以下幾點：

表3 雙參數米塔-列夫勒函數任意階導數的全局帕德逼近Tab.3 Global Padéapproximation for any derivative of two-parameter Mittag-Leffler functions

（1）階導數的泰勒級數和漸進級數的加權項：

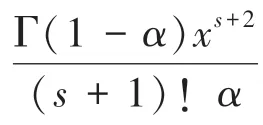
（2）經Matlab軟件編程求解，可知階導數的階全局帕德逼近系數p（0，1，…，1）：

當{0≤1，}時：…＝p＝p＝0；

當｛01｝時：…＝p＝p0。

（3）當階數2時，可直接手算解出系數p和q的表達式。當階數2時，難以手算求解，系數p和q（0，1…，1）（除p＝0之外）的表達式隨著的增大而越復雜，此時可借助Matlab軟件求解。系數p和q的表達式只與參數和有關，因此可根據參數和的取值，預先計算系數p和q的值并存入矩陣中，以優化精度、計算時間和系統內存。

3.2 仿真結果及分析

當{0≤1，≤，0}時，通過Matlab 軟件可求解任意階導數的全局帕德逼近式。為了探究全局帕德逼近算法的準確性，不妨將全局帕德逼近式的計算結果與文獻［35］中_（）函數的計算結果相比較，仿真結果如圖5～圖8所示。_（）函數能求解1到4參數（、、、）的米塔-列夫勒函數及其導數，是目前唯一能夠求解任意階米塔-列夫勒函數導數的可用代碼。

為探究導數階數和逼近階數對逼近效果的影響，繪制E（）的一階、二階、三階導數在不同逼近階數下的相對誤差曲線，可見圖5～圖7。

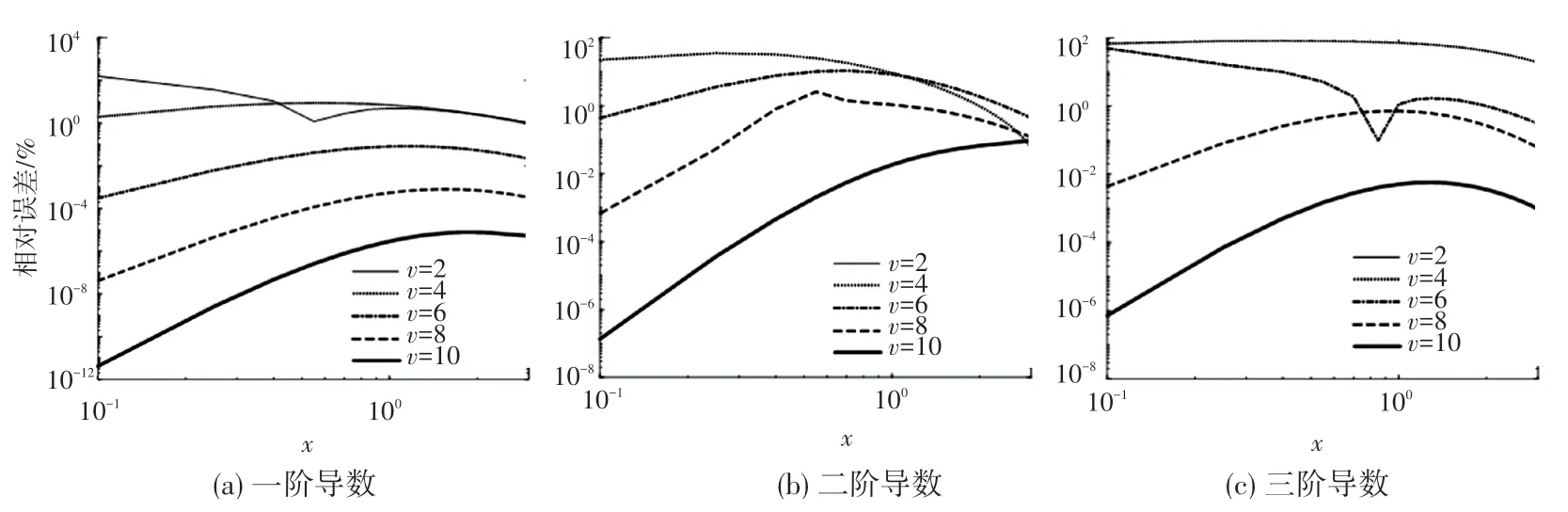
圖7 α＝0.47，β＝0.47，x∈［0，3］Fig.7 α＝0.47，β＝0.47，x∈［0，3］

為了探究和取值向1趨近時的逼近效果，這里取｛05，07，09｝，繪制dE（）d（）的10階全局帕德逼近曲線、_（）函數曲線以及兩者的相對誤差曲線，可見圖8。

觀察圖5～圖8，得到結論：

（1）全局帕德逼近算法的逼近階數越高，誤差越小，逼近效果越好。

（2）米塔-列夫勒函數的導數階數越高，達到相同逼近效果所需的逼近階數越高。圖5中，一階導數的四階逼近的相對誤差大小和三階導數的六階逼近的差不多。

圖5 α＝1，β＝8，x∈［0，20］Fig.5 α＝1，β＝8，x∈［0，20］

（3）當{01}時，和取值越接近于1，逼近效果越差。圖8中，在相同條件下，和取值越大，相對誤差越大。當05時，最大相對誤差低于110。當09時，最大相對誤差超過1×10%。

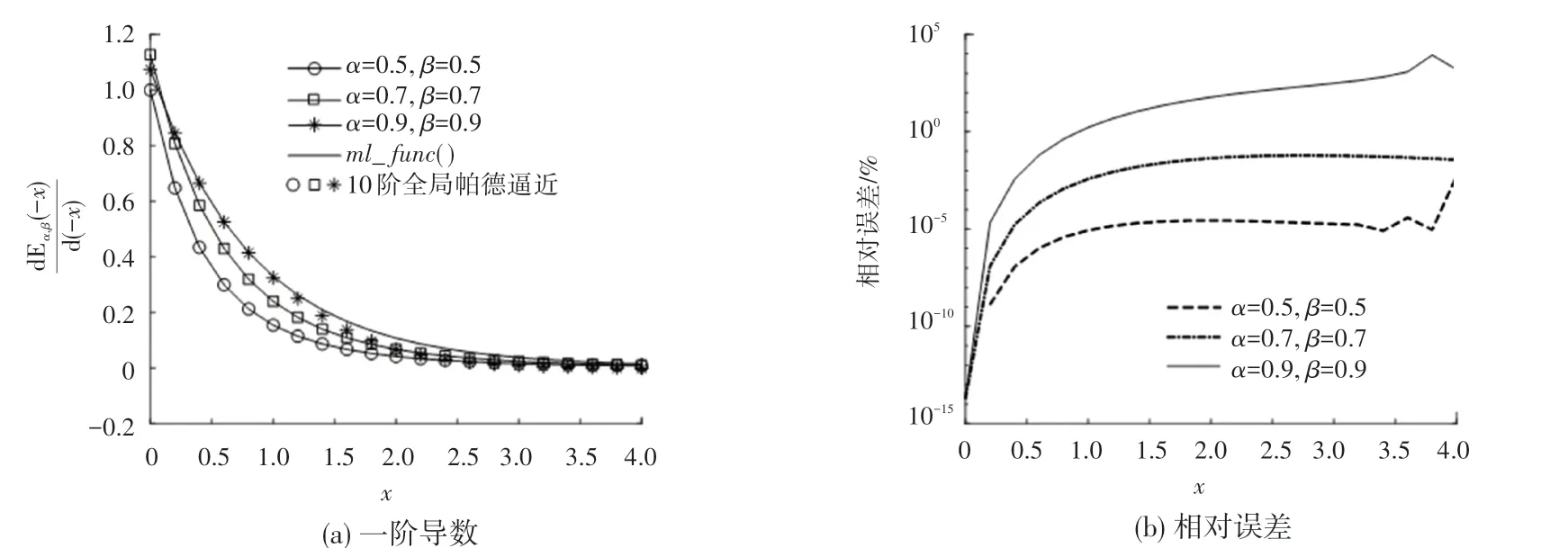
圖8 α和β對逼近效果的影響Fig.8 The effect ofαandβon the approximation

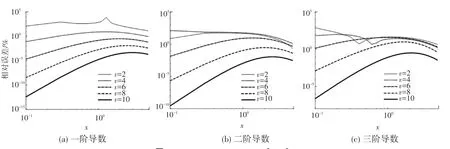
圖6 α＝0.65，β＝0.95，x∈［0，5］Fig.6 α＝0.65，β＝0.95，x∈［0，5］

4 結束語

米塔-列夫勒函數類的表示、快速有效高精度計算、顯示、應用是近年來的研究熱點。本文基于全局帕德逼近技術構造雙參數米塔-列夫勒函數E（）及其任意階導數dE（）d（）（∈?）的數值算法，從泰勒級數和漸進級數出發實現高階全局帕德逼近。根據和的取值，分2種情況計算：｛0≤1，｝和｛01｝，理論分析并求解全局帕德逼近式。通過大量仿真實驗，證明了全局帕德逼近算法的逼近性能優越，數值求解結果穩定可靠。逼近階數越高，逼近效果越好，10階逼近的計算精度可達110；導數階數越高，達到指定精度所需的逼近階數越高。