翼型動(dòng)態(tài)失速氣動(dòng)力二次峰值數(shù)值模擬研究

井思?jí)簦w國(guó)慶，招啟軍

（南京航空航天大學(xué)直升機(jī)旋翼動(dòng)力學(xué)國(guó)家級(jí)重點(diǎn)實(shí)驗(yàn)室，南京 210016）

動(dòng)態(tài)失速是一種非定常流動(dòng)分離現(xiàn)象，通常發(fā)生在大拉力或機(jī)動(dòng)飛行狀態(tài)的直升機(jī)旋翼上。動(dòng)態(tài)失速一旦發(fā)生，會(huì)引起升力突降、旋翼反扭矩和槳葉振動(dòng)突增等問題，從而限制直升機(jī)的最大飛行速度和機(jī)動(dòng)性能。因此，動(dòng)態(tài)失速機(jī)理一直是旋翼空氣動(dòng)力學(xué)領(lǐng)域的研究熱點(diǎn)之一。

迄今，許多學(xué)者針對(duì)翼型開展了動(dòng)態(tài)失速機(jī)理的研究［1?3］。通過試驗(yàn)測(cè)量翼型的氣動(dòng)載荷以及流場(chǎng)特性，可以直觀地了解翼型動(dòng)態(tài)失速過程中氣動(dòng)力的遲滯效應(yīng)以及動(dòng)態(tài)失速渦的發(fā)展。McCros?key 等［4］測(cè)量了NACA0012 翼型及其前緣修型翼型的動(dòng)態(tài)失速特性，發(fā)現(xiàn)渦脫落現(xiàn)象是不同類型動(dòng)態(tài)失速的主要共同特征。Wang 等［5］采用PIV 技術(shù)測(cè)量了OA209 和SC1095 翼型前緣渦的輸運(yùn)速度，研究表明前緣渦的輸運(yùn)速度主要受到翼型振蕩頻率的影響，當(dāng)振蕩頻率增加時(shí)，前緣渦的輸運(yùn)速度也會(huì)提升。Geissler 等［6］開展了OA312 翼型動(dòng)態(tài)失速特性的試驗(yàn)和數(shù)值模擬研究，發(fā)現(xiàn)渦量的發(fā)展、脫落和積累對(duì)翼型的動(dòng)態(tài)失速特性有重要影響。

由于翼型動(dòng)態(tài)失速的風(fēng)洞試驗(yàn)較為復(fù)雜，成本高，且受到測(cè)量設(shè)備、技術(shù)的限制，因此只能開展有限工況下的研究。隨著計(jì)算流體力學(xué)的發(fā)展，數(shù)值模擬逐漸成為翼型動(dòng)態(tài)失速特性研究的主要途徑［7?10］。

為了研究翼型外形對(duì)動(dòng)態(tài)失速特性的影響規(guī)律，一些學(xué)者開展了相應(yīng)的研究。王清等［11］和鄒錦華等［12］開展了翼型前緣外形對(duì)動(dòng)態(tài)失速特性的影響規(guī)律研究，結(jié)果表明：上翼面前緣外形對(duì)翼型的動(dòng)態(tài)失速特性有顯著影響，并且合理的變形能夠抑制翼型的動(dòng)態(tài)失速。王友進(jìn)等［13］針對(duì)翼型厚度對(duì)動(dòng)態(tài)失速特性的影響開展了數(shù)值模擬分析，研究發(fā)現(xiàn)：薄翼型的動(dòng)態(tài)失速是由前緣分離引起的，而厚翼型的動(dòng)態(tài)失速則是由后緣分離引起的，并在分離區(qū)域向翼型前緣擴(kuò)展的過程中發(fā)生失速。Shar?ma 等［14］模擬分析了NACA 系列不同厚度對(duì)稱翼型在低雷諾數(shù)下的動(dòng)態(tài)失速特性，結(jié)果表明：較薄的NACA0009 翼型的動(dòng)態(tài)失速是由層流分離泡的破裂引起的，而最厚的NACA0018 翼型的動(dòng)態(tài)失速則是由湍流邊界層的分離引起的。

此外，氣動(dòng)參數(shù)以及翼型運(yùn)動(dòng)參數(shù)對(duì)翼型的動(dòng)態(tài)失速特性也有顯著影響。Kim 等［15］和孔衛(wèi)紅等［16］開展了壓縮性效應(yīng)對(duì)翼型動(dòng)態(tài)失速特性的影響研究，分析表明：小馬赫數(shù)下壓縮性效應(yīng)的影響較小，而在高馬赫數(shù)下，壓縮性效應(yīng)對(duì)翼型的動(dòng)態(tài)失速特性起主導(dǎo)作用。宋辰瑤等［17］、趙國(guó)慶等［18］和楊鶴森等［19］對(duì)翼型動(dòng)態(tài)失速特性開展了參數(shù)影響研究，揭示了平均迎角、迎角振幅及縮減頻率等振蕩參數(shù)以及雷諾數(shù)和馬赫數(shù)等氣動(dòng)參數(shù)對(duì)氣動(dòng)力遲滯效應(yīng)以及氣動(dòng)力峰值的影響規(guī)律。

直升機(jī)旋翼翼型工作的縮減頻率一般在0.03～0.15 之間，趙國(guó)慶等［18］針對(duì)縮減頻率為0.05，0.10 和0.15 等3 個(gè)典型工況下的旋翼翼型動(dòng)態(tài)失速特性開展了數(shù)值模擬研究。分析表明：縮減頻率表征了旋翼翼型動(dòng)態(tài)失速特性的強(qiáng)弱程度，對(duì)旋翼翼型動(dòng)態(tài)失速的遲滯效應(yīng)、氣動(dòng)力系數(shù)峰值和失速迎角具有重要影響。當(dāng)縮減頻率為0.05 時(shí)，除了動(dòng)態(tài)失速渦引起的氣動(dòng)力峰值外，翼型的氣動(dòng)力系數(shù)曲線還出現(xiàn)了二次峰值，然而文中并未開展對(duì)氣動(dòng)力二次峰值的細(xì)致研究。Mcalister 等［20］針對(duì)翼型動(dòng)態(tài)失速的試驗(yàn)研究也表明：在某些動(dòng)態(tài)失速狀態(tài)下，翼型的氣動(dòng)力會(huì)出現(xiàn)明顯的二次峰值。Choudhry 等［21］對(duì)動(dòng)態(tài)失速升力特征進(jìn)行了系統(tǒng)的綜述研究，分析了低雷諾數(shù)下翼型以恒定速度抬頭至指定迎角過程中的動(dòng)態(tài)失速現(xiàn)象和升力變化，發(fā)現(xiàn)了由二次渦結(jié)構(gòu)引起的升力二次峰值現(xiàn)象。

目前，在翼型動(dòng)態(tài)失速機(jī)理方面，相關(guān)學(xué)者已經(jīng)做了大量的研究工作。然而，針對(duì)翼型動(dòng)態(tài)失速氣動(dòng)力二次峰值的研究工作相對(duì)較少。因此，本文建立了翼型非定常流場(chǎng)數(shù)值模擬方法，在此基礎(chǔ)上開展了翼型動(dòng)態(tài)失速氣動(dòng)力二次峰值的機(jī)理研究，并著重分析了翼型厚度、彎度及彎度位置等參數(shù)對(duì)氣動(dòng)力二次峰值的影響，獲得了一些有意義的結(jié)論。

1 翼型非定常流場(chǎng)數(shù)值模擬方法

1.1 網(wǎng)格生成方法

通過求解泊松方程來生成圍繞翼型的C 型網(wǎng)格，將泊松方程離散化后可以得到

圖1 給出了圍繞SC1095 翼型的C 型網(wǎng)格。從圖1 可以看出，翼型網(wǎng)格具有良好的正交性和貼體性。

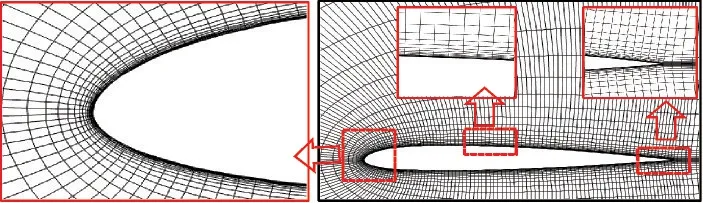
圖1 圍繞SC1095 翼型的C 型網(wǎng)格Fig.1 C?type grid around SC1095 airfoil

為了模擬翼型俯仰振蕩時(shí)的非定常氣動(dòng)特性，采用運(yùn)動(dòng)嵌套網(wǎng)格技術(shù)實(shí)現(xiàn)翼型網(wǎng)格的運(yùn)動(dòng)以及翼型網(wǎng)格和背景網(wǎng)格之間的信息交換。采用Hole?Map 方法確定背景網(wǎng)格在翼型網(wǎng)格上的洞邊界，采用Inverse?Map 方法進(jìn)行背景網(wǎng)格人工內(nèi)邊界的貢獻(xiàn)單元搜索。圖2 給出了運(yùn)動(dòng)嵌套網(wǎng)格系統(tǒng)示意圖。

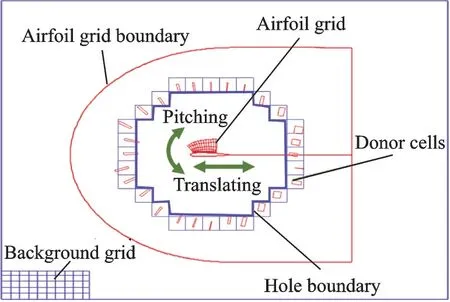
圖2 運(yùn)動(dòng)嵌套網(wǎng)格系統(tǒng)Fig.2 Moving?embedded grid system

1.2 流動(dòng)控制方程及求解方法

采用積分形式的RANS 方程作為翼型流場(chǎng)的控制方程

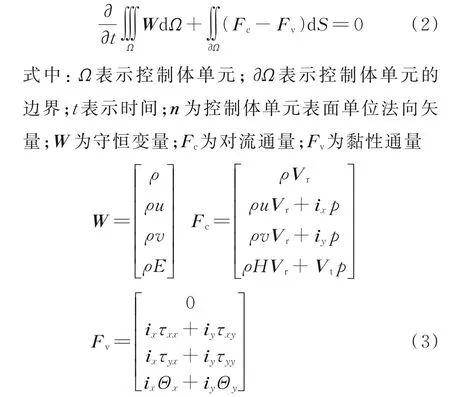
式中：ρ表示密度；p表示壓強(qiáng)；E和H分別表示單位質(zhì)量的總能和總焓；Vr和Vt分別表示相對(duì)運(yùn)動(dòng)速度和由網(wǎng)格運(yùn)動(dòng)引起的牽連速度，且Vr=VVt，其中V表示絕對(duì)運(yùn)動(dòng)速度；ix與iy分別為x與y方向的單位矢量；τij為黏性應(yīng)力；Θi為描述黏性和熱傳導(dǎo)的作用項(xiàng)。

采用CLORNS 求解器［22］對(duì)流場(chǎng)控制方程進(jìn)行求解。空間離散采用Roe 格式，網(wǎng)格面兩側(cè)的流場(chǎng)原始變量采用三階MUSCL 格式進(jìn)行重構(gòu)，時(shí)間推進(jìn)采用LU?SGS 隱式格式。為了較好地模擬大迎角下翼型的氣流分離和失速特性，采用S?A 湍流模型模擬流場(chǎng)的黏性系數(shù)，實(shí)現(xiàn)控制方程的封閉。

1.3 方法驗(yàn)證

采用所建立的CFD 方法對(duì)NACA0012 翼型在深度失速狀態(tài)下的氣動(dòng)特性進(jìn)行了模擬。迎角變化規(guī)律為α=14.91°+9.88°sin（2kt），來流馬赫數(shù)Ma為0.283，縮減頻率k=0.151，雷諾數(shù)Re=3.4×106，t為時(shí)間。在該算例中，計(jì)算域設(shè)置如圖3 所示，翼型表面采用無滑移和絕熱條件，背景網(wǎng)格外邊界采用無反射遠(yuǎn)場(chǎng)邊界條件。在劃分翼型網(wǎng)格時(shí)，設(shè)置壁面第一層網(wǎng)格單元高度為4×10-6c，保證y+≈1。圖4 給出了3 套不同網(wǎng)格的氣動(dòng)力系數(shù)計(jì)算值與試驗(yàn)值［20］的對(duì)比，3 套網(wǎng)格的信息在表1中給出。從圖4 中可以看出：計(jì)算值與試驗(yàn)值吻合較好，表明本文的數(shù)值模擬方法能夠準(zhǔn)確地模擬翼型的動(dòng)態(tài)失速特性；并且，在翼型上仰過程中，3 套網(wǎng)格的計(jì)算結(jié)果一致，在下俯過程中，中等網(wǎng)格和密網(wǎng)格的計(jì)算結(jié)果基本重合。因此，在后文的研究中，均采用了與此算例中等網(wǎng)格相同的網(wǎng)格量。

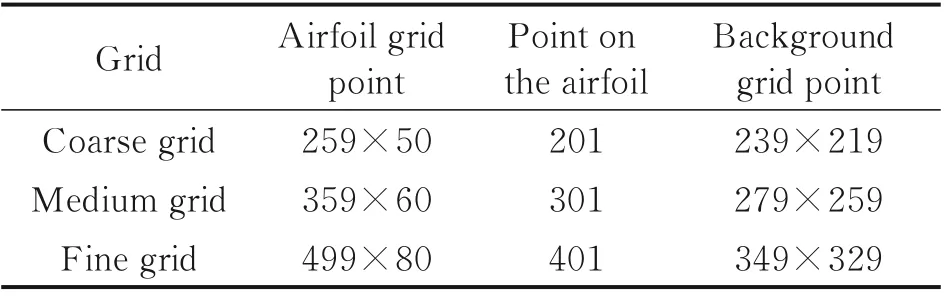
表1 NACA0012 翼型網(wǎng)格信息Table 1 Information about the three sets of grids

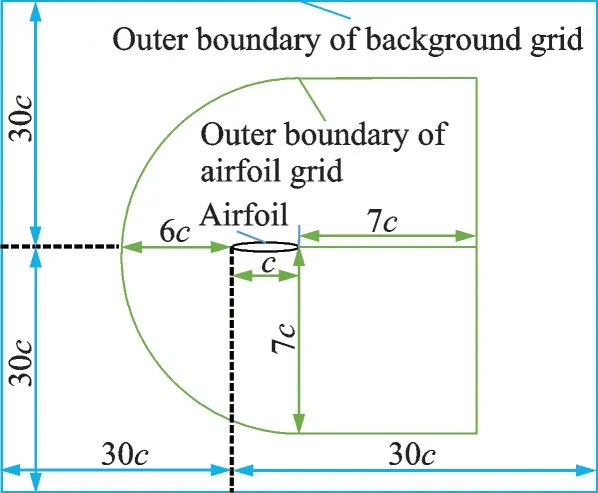
圖3 計(jì)算域示意圖Fig.3 Schematic diagram of computational domain

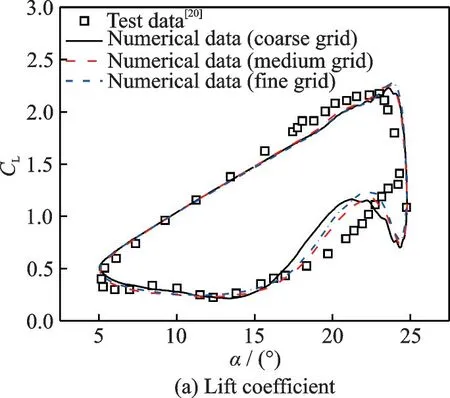
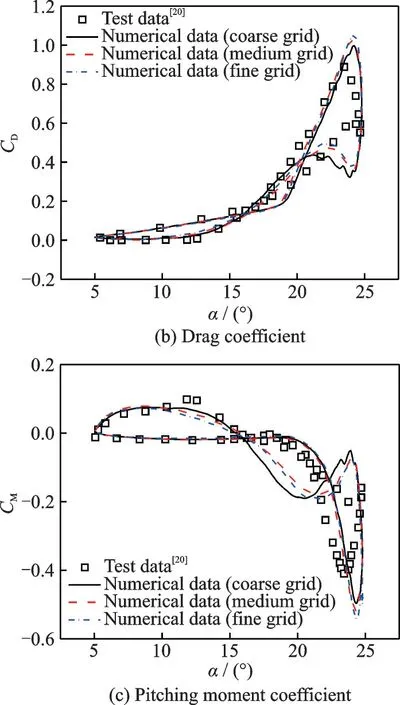
圖4 翼型氣動(dòng)力系數(shù)計(jì)算值與試驗(yàn)值[20]對(duì)比Fig.4 Comparison of aerodynamic force coefficients be?tween calculated results and test data[20]

2 動(dòng)態(tài)失速氣動(dòng)力二次峰值分析

為了探究翼型動(dòng)態(tài)失速狀態(tài)下氣動(dòng)力二次峰值的發(fā)生機(jī)理，對(duì)NACA0012 翼型在狀態(tài)Ma=0.293，α=14.82°+9.90°sin（2kt），k=0.051，Re=3.82×106下的動(dòng)態(tài)失速特性進(jìn)行了模擬分析。

圖5 給出了NACA0012 翼型的升力、阻力和力矩系數(shù)曲線，圖中A～F為6 個(gè)不同時(shí)刻。從圖5中可以看出，NACA0012 翼型在此狀態(tài)下發(fā)生了深度失速，并且失速后升力、阻力和力矩系數(shù)出現(xiàn)了二次峰值。

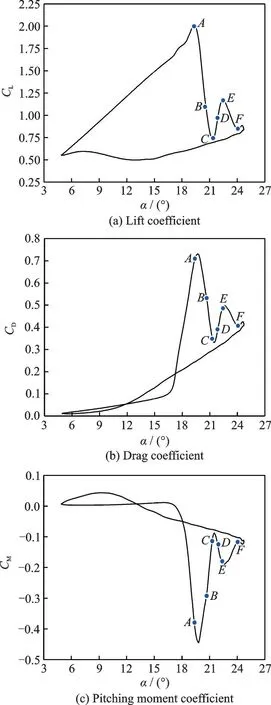
圖5 NACA0012 翼型氣動(dòng)力系數(shù)Fig.5 Aerodynamic force coefficients of NACA0012 airfoil

圖6 給出了圖5 中6 個(gè)不同時(shí)刻（A～F）NA?CA0012 翼型的壓強(qiáng)系數(shù)分布云圖和流線圖。不同時(shí)刻對(duì)應(yīng)的翼型迎角如表2 所示。不同時(shí)刻翼型表面的壓強(qiáng)系數(shù)分布如圖7 所示。

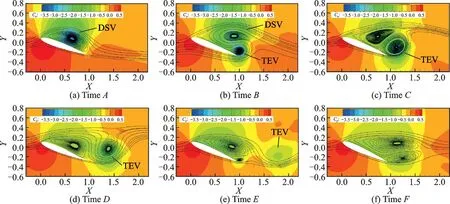
圖6 NACA0012 翼型壓強(qiáng)分布云圖和流線圖Fig.6 Pressure coefficient cloud and freestream lines of NACA0012 airfoil

圖7 NACA0012 翼型壓強(qiáng)系數(shù)分布Fig.7 Pressure coefficient distribution of NACA0012 airfoil

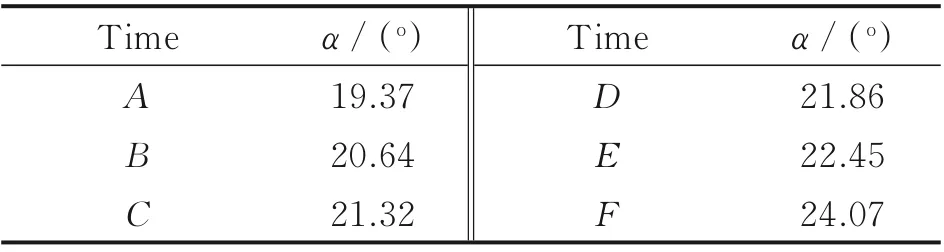
表2 不同時(shí)刻的翼型迎角Table 2 Angles of attack of airfoil at different time

從圖6 可以看出，在A時(shí)刻，翼型上表面已經(jīng)形成了動(dòng)態(tài)失速渦（Dynamic stall vortex，DSV），而且翼型上表面中部出現(xiàn)了由動(dòng)態(tài)失速渦導(dǎo)致的局部負(fù)壓區(qū)域。動(dòng)態(tài)失速渦在翼型前緣附近形成后，會(huì)沿著翼型上表面向后緣移動(dòng)。一方面，當(dāng)動(dòng)態(tài)失速渦附著于翼型表面時(shí)，渦致升力的存在會(huì)使得翼型升力系數(shù)持續(xù)增加；另一方面，負(fù)壓中心也在向后緣移動(dòng)，導(dǎo)致低頭力矩逐漸增加。接著，動(dòng)態(tài)失速渦會(huì)從翼型表面脫落，渦致升力開始減小，同時(shí)，前緣負(fù)壓峰值減小，二者共同作用導(dǎo)致升力系數(shù)下降，阻力、低頭力矩進(jìn)一步增加。在A時(shí)刻，動(dòng)態(tài)失速渦即將從翼型表面脫落，此時(shí)翼型的升力系數(shù)達(dá)到峰值，阻力和低頭力矩系數(shù)接近峰值，如圖5 所示。

在B時(shí)刻，動(dòng)態(tài)失速渦誘導(dǎo)形成了后緣渦（Trailing?edge vortex，TEV），導(dǎo)致后緣附近局部負(fù)壓峰值的出現(xiàn)，如圖7（a）所示。在主流和后緣渦的作用下，動(dòng)態(tài)失速渦向上抬升，脫離翼型表面，使得由動(dòng)態(tài)失速渦引起的局部負(fù)壓減小，進(jìn)而導(dǎo)致升力系數(shù)的突降。從圖7（a）可以看出，與A時(shí)刻相比，B時(shí)刻翼型前緣負(fù)壓峰值減小，同時(shí)翼型中部動(dòng)態(tài)失速渦引起的局部負(fù)壓減小，并且后緣渦引起了新的局部負(fù)壓，使得翼型的阻力系數(shù)和低頭力矩系數(shù)減小。

在C時(shí)刻，動(dòng)態(tài)失速渦的強(qiáng)度進(jìn)一步減弱，在后緣渦的作用下，動(dòng)態(tài)失速渦又逐漸向翼型上表面靠攏。后緣渦上洗并膨脹，強(qiáng)度也逐漸減弱。此時(shí)，翼型的升、阻力系數(shù)和低頭力矩系數(shù)進(jìn)一步減小。

在D時(shí)刻，后緣渦上洗，從翼型后緣脫落并向下游移動(dòng)至尾跡區(qū)，由后緣渦引起的局部負(fù)壓消失。由于后緣渦的誘導(dǎo)作用，動(dòng)態(tài)失速渦繼續(xù)向翼型上表面靠攏，并重新附著于翼型上表面。此時(shí)，動(dòng)態(tài)失速渦較弱，在翼型表面并沒有形成明顯的局部負(fù)壓。但是，如圖7（b）所示，與C時(shí)刻相比，D時(shí)刻的前緣負(fù)壓峰值和翼型上表面負(fù)壓明顯增加，導(dǎo)致升力、阻力和力矩系數(shù)回升。

由圖7（b）可知，在E時(shí)刻，翼型前緣負(fù)壓峰值和上表面負(fù)壓較D時(shí)刻進(jìn)一步增加。此時(shí)，翼型升、阻力系數(shù)和低頭力矩系數(shù)達(dá)到二次峰值。同時(shí)，從圖6（e）可以看出，由于動(dòng)態(tài)失速渦的誘導(dǎo)作用，翼型后緣附近形成了新的較弱的后緣渦。

在F時(shí)刻，動(dòng)態(tài)失速渦向上抬升，遠(yuǎn)離翼型表面，分離區(qū)域擴(kuò)大，氣流分離加劇，導(dǎo)致前緣負(fù)壓峰值和翼型上表面負(fù)壓的減小，從而導(dǎo)致升力、阻力和力矩系數(shù)的下降。

總體而言，動(dòng)態(tài)失速渦的形成，導(dǎo)致第一個(gè)氣動(dòng)力峰值的出現(xiàn)；動(dòng)態(tài)失速渦誘導(dǎo)形成后緣渦，在后緣渦的作用下，動(dòng)態(tài)失速渦向翼型表面靠攏，并重新附著于翼型上表面，導(dǎo)致翼型氣動(dòng)力二次峰值的出現(xiàn)。

3 翼型外形對(duì)氣動(dòng)力二次峰值的影響分析

為了探究翼型外形對(duì)氣動(dòng)力二次峰值的影響，對(duì)NACA 系列不同厚度、彎度和彎度位置的翼型開展了氣動(dòng)特性模擬分析。計(jì)算狀態(tài)同第2 節(jié)。

3.1 翼型厚度影響

為了探究翼型厚度對(duì)氣動(dòng)力二次峰值的影響，對(duì)NACA0009、NACA0012 和NACA0015 這3 個(gè)不同厚度翼型的動(dòng)態(tài)失速特性進(jìn)行了模擬分析。翼型外形對(duì)比如圖8 所示。

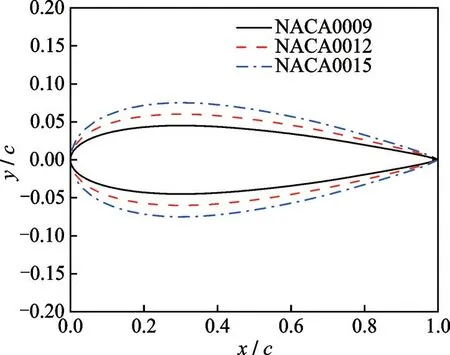
圖8 不同厚度翼型外形對(duì)比Fig.8 Comparison of airfoils with different thicknesses

圖9 給出了NACA0009、NACA0012 和NA?CA0015 這3 個(gè)不同厚度翼型的氣動(dòng)力系數(shù)對(duì)比。從圖中可以看出，翼型厚度對(duì)動(dòng)態(tài)失速特性有顯著的影響。翼型厚度增加，動(dòng)態(tài)失速迎角增加，升力、阻力和低頭力矩系數(shù)峰值均增加。在線性升力段，相同迎角下厚度較大的翼型產(chǎn)生的升力較小，且厚度對(duì)線性段升力線斜率的影響較小。此外，3 個(gè)不同厚度翼型在此動(dòng)態(tài)失速狀態(tài)下均出現(xiàn)了氣動(dòng)力二次峰值。本文稱兩個(gè)峰值之間的氣動(dòng)力最小值為谷值，由圖9 可知，翼型厚度越大，二次峰值出現(xiàn)的越晚，且二次峰值相對(duì)谷值的增量（下文簡(jiǎn)稱“二次峰值增量”）越大。

圖9 不同厚度翼型的氣動(dòng)力系數(shù)對(duì)比Fig.9 Comparison of aerodynamic force coefficients of airfoils with different thicknesses

圖10 給出了3 個(gè)翼型的壓強(qiáng)系數(shù)分布云圖和流線圖。從圖10 中可以看出，在翼型上仰過程中迎角為18.00°的狀態(tài)下，NACA0009 翼型上表面已經(jīng)形成了動(dòng)態(tài)失速渦，且動(dòng)態(tài)失速渦移動(dòng)至后緣附近，誘導(dǎo)形成了后緣渦。此時(shí)，NACA0012 翼型前緣形成了動(dòng)態(tài)失速渦，而NACA0015 翼型的流動(dòng)仍附著在翼型表面，沒有發(fā)生明顯的氣流分離。當(dāng)迎角增加至20.23°，NACA0012 翼型上表面的動(dòng)態(tài)失速渦移動(dòng)至后緣附近，誘導(dǎo)形成了后緣渦。此時(shí)，NACA0015 翼型后緣發(fā)生了氣流分離。當(dāng)迎角繼續(xù)增加至21.78°，NACA0015 翼型上表面形成了動(dòng)態(tài)失速渦，NACA0012 翼型的后緣渦脫落至尾跡區(qū)。

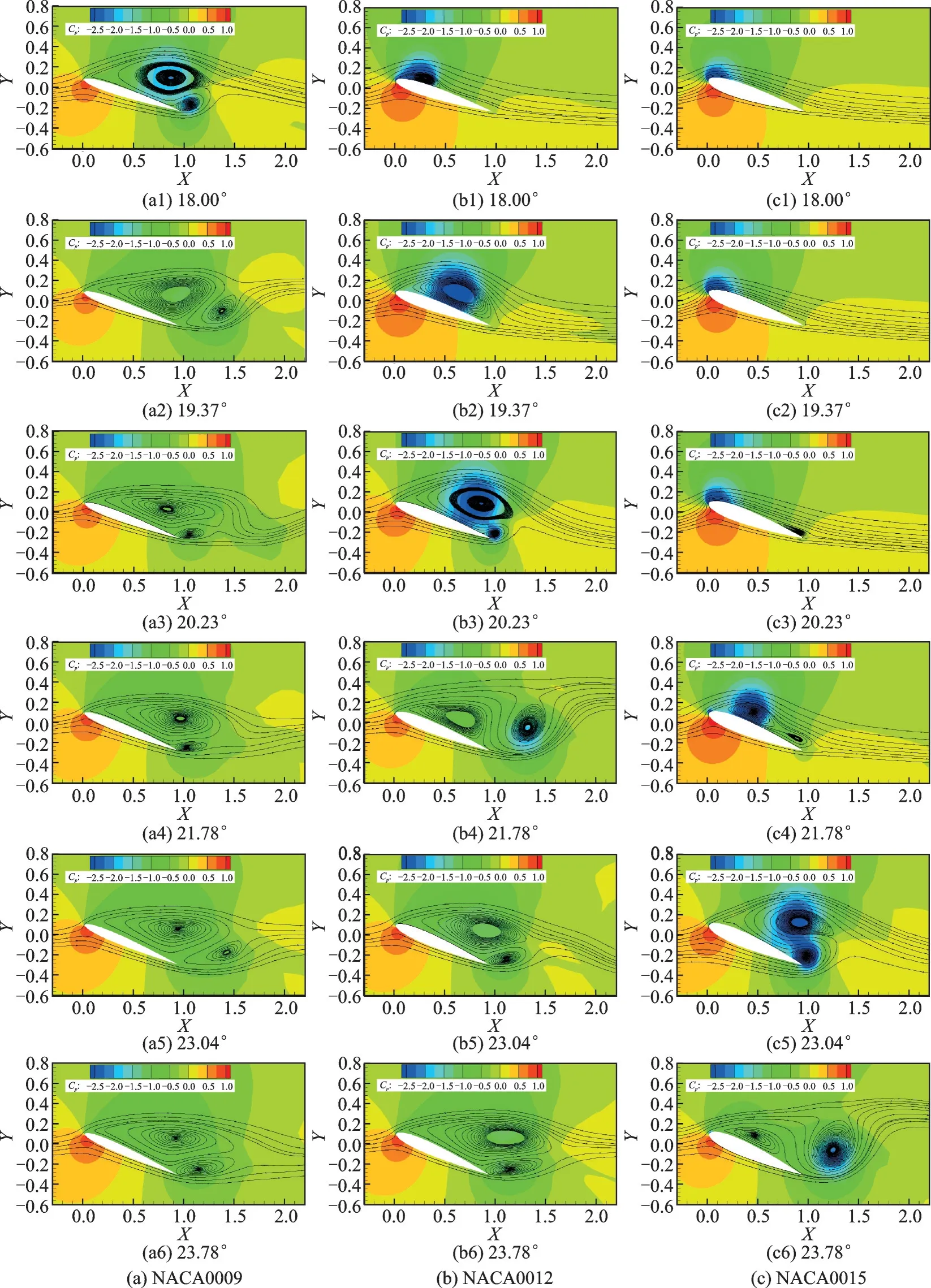
圖10 不同厚度翼型的壓強(qiáng)分布云圖和流線圖對(duì)比Fig.10 Comparison of pressure coefficient cloud and streamlines of airfoils with different thicknesses

NACA0009、NACA0012 和NACA0015 翼型上表面先后形成了不同強(qiáng)度的動(dòng)態(tài)失速渦和后緣渦，動(dòng)態(tài)失速渦和后緣渦相互作用，導(dǎo)致翼型氣動(dòng)力出現(xiàn)二次峰值。翼型厚度增加，推遲了動(dòng)態(tài)失速渦和后緣渦的形成，從而推遲了氣動(dòng)力二次峰值的出現(xiàn)。此外，3 個(gè)翼型在此狀態(tài)下均發(fā)生了前緣失速，翼型厚度增加，形成的動(dòng)態(tài)失速渦和后緣渦強(qiáng)度增加，導(dǎo)致氣動(dòng)力二次峰值增量增加。

3.2 翼型彎度影響

為了探究翼型彎度對(duì)翼型動(dòng)態(tài)失速狀態(tài)氣動(dòng)力二次峰值的影響，對(duì)NACA0012、NACA2212 和NACA4212 這3 個(gè)不同彎度翼型的動(dòng)態(tài)失速特性進(jìn)行了模擬分析。翼型外形對(duì)比如圖11 所示。

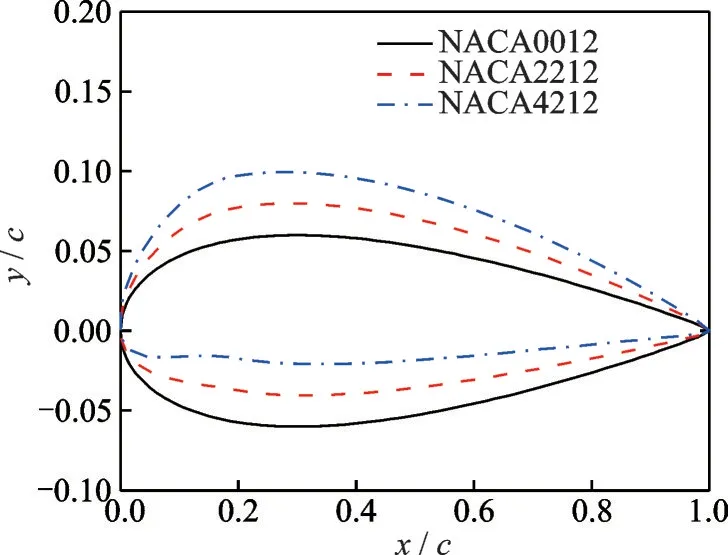
圖11 不同彎度翼型外形對(duì)比Fig.11 Comparison of airfoils with different cambers

圖12 給出了NACA0012、NACA2212 和NA?CA4212 這3 個(gè)不同彎度翼型的氣動(dòng)力系數(shù)對(duì)比。從圖12 中可以看出，彎度對(duì)翼型動(dòng)態(tài)失速特性有明顯影響。迎角相同時(shí)，彎度較大的翼型產(chǎn)生的升力系數(shù)越大，低頭力矩系數(shù)也越大。隨著翼型彎度的增加，動(dòng)態(tài)失速迎角、阻力和力矩發(fā)散迎角增加，氣動(dòng)力系數(shù)峰值呈現(xiàn)先增加后減小的趨勢(shì)。NA?CA0012 和NACA2212 翼型的氣動(dòng)力系數(shù)出現(xiàn)了明顯的二次峰值，而NACA4212 翼型的二次峰值則較小。而且，翼型彎度越大，翼型升力系數(shù)二次峰值出現(xiàn)的越晚，二次峰值增量呈現(xiàn)先增加后減小的趨勢(shì)，并且與NACA0012 和NACA2212 翼型相比，NACA4212 翼型的升、阻力和力矩系數(shù)二次峰值增量均最小。

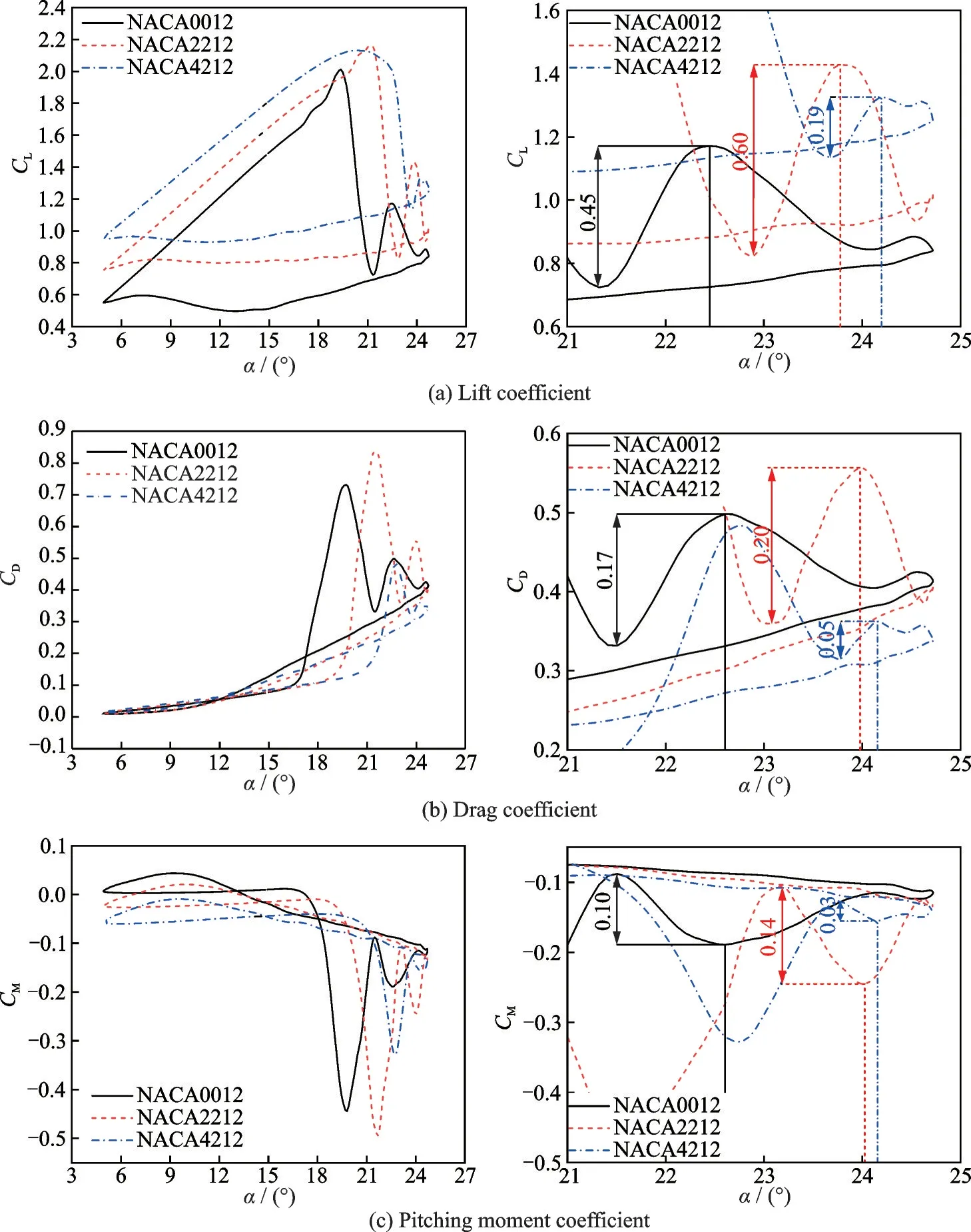
圖12 不同彎度翼型的氣動(dòng)力系數(shù)對(duì)比Fig.12 Comparison of aerodynamic force coefficients of airfoils with different cambers

圖13 給出了3 個(gè)翼型在不同時(shí)刻的壓強(qiáng)系數(shù)分布云圖和流線圖。從圖13 中可以看出，NA?CA0012 和NACA2212 翼型先后發(fā)生了前緣失速，即動(dòng)態(tài)失速渦在翼型前緣附近形成。而NA?CA4212 翼型則先出現(xiàn)了后緣氣流分離，隨著迎角的增加，分離點(diǎn)向上游移動(dòng)，并在翼型中后部形成了動(dòng)態(tài)失速渦。由于動(dòng)態(tài)失速渦的誘導(dǎo)作用，3 個(gè)翼型后緣附近形成了不同強(qiáng)度的后緣渦。當(dāng)翼型發(fā)生前緣動(dòng)態(tài)失速時(shí)，翼型彎度的增加會(huì)推遲動(dòng)態(tài)失速渦和后緣渦的形成，從而推遲二次峰值的出現(xiàn)；且彎度增加會(huì)增強(qiáng)動(dòng)態(tài)失速渦和后緣渦的強(qiáng)度，從而導(dǎo)致二次峰值增量增加。而當(dāng)彎度增加到一定程度，翼型上表面后緣附近的曲率變化較大，導(dǎo)致翼型失速類型轉(zhuǎn)變?yōu)楹缶壥伲c前緣失速情況相比，后緣失速情況下形成的動(dòng)態(tài)失速渦和后緣渦的強(qiáng)度較小，因此氣動(dòng)力系數(shù)二次峰值增量較小。

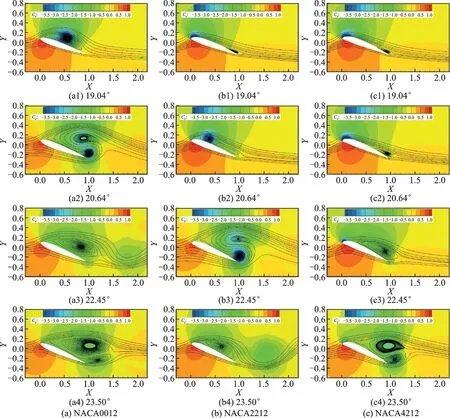
圖13 不同彎度翼型的壓強(qiáng)系數(shù)分布云圖和流線圖Fig.13 Comparison of pressure coefficient cloud and streamlines of airfoils with different cambers

3.3 翼型彎度位置影響

為了探究翼型彎度位置對(duì)動(dòng)態(tài)失速氣動(dòng)力二次峰值的影響，對(duì)NACA2212、NACA2412 和NACA2612 這3 個(gè)不同彎度位置翼型的動(dòng)態(tài)失速特性進(jìn)行了模擬分析。翼型外形對(duì)比如圖14所示。

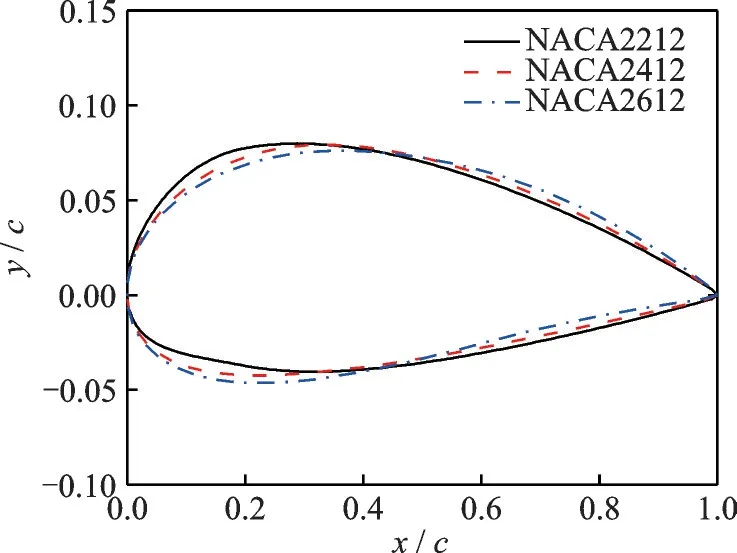
圖14 不同彎度位置翼型外形對(duì)比Fig.14 Comparison of airfoils with different positions of camber

圖15 給出了3 個(gè)不同彎度位置翼型的氣動(dòng)力系數(shù)對(duì)比。在線性升力段相同迎角下，彎度位置靠后的翼型產(chǎn)生的升力系數(shù)較大，低頭力矩系數(shù)也較大。隨著彎度位置的增加，翼型的動(dòng)態(tài)失速迎角、阻力和力矩發(fā)散迎角減小，氣動(dòng)力系數(shù)峰值也有所減小。彎度位置越靠后，二次峰值出現(xiàn)得越早，且二次峰值增量越小。

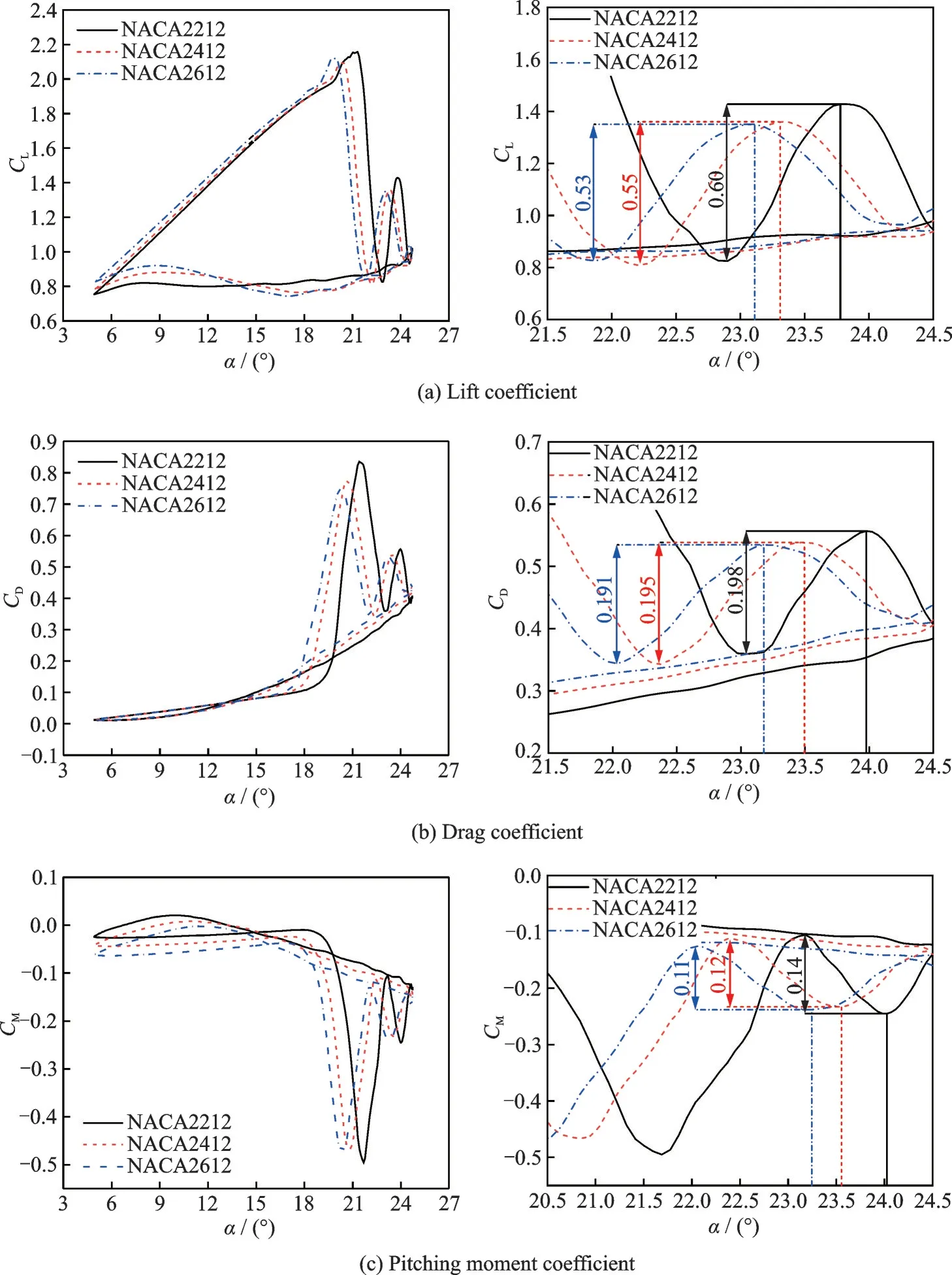
圖15 不同彎度位置翼型的氣動(dòng)力系數(shù)對(duì)比Fig.15 Comparison of aerodynamic force coefficients of airfoils with different positions of camber

圖16 給出了3 個(gè)翼型的壓強(qiáng)系數(shù)分布云圖和流線圖。從圖16 中可以看出，3 個(gè)翼型都發(fā)生了前緣失速，且彎度位置越靠后，動(dòng)態(tài)失速發(fā)生的越早，后緣渦的形成也越早，導(dǎo)致二次峰值出現(xiàn)的越早。而且，彎度位置越靠后，動(dòng)態(tài)失速渦和后緣渦的強(qiáng)度越小，從而導(dǎo)致翼型氣動(dòng)力系數(shù)二次峰值增量越小。

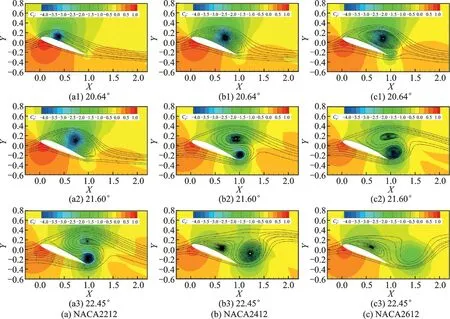
圖16 不同彎度位置翼型的壓強(qiáng)系數(shù)分布云圖和流線圖Fig.16 Comparison of pressure coefficient cloud and streamlines of airfoils with different positions of camber

4 結(jié)論

基于URANS 方程，結(jié)合運(yùn)動(dòng)嵌套網(wǎng)格技術(shù)、LU?SGS 隱式格式、Roe?MUSCL 數(shù)值格式和S?A湍流模型，建立了翼型非定常氣動(dòng)特性數(shù)值模擬方法，開展了翼型動(dòng)態(tài)失速氣動(dòng)力二次峰值機(jī)理研究和參數(shù)影響分析。綜合計(jì)算分析結(jié)果，得出結(jié)論如下：

（1）在動(dòng)態(tài)失速過程中，翼型上表面會(huì)形成動(dòng)態(tài)失速渦，導(dǎo)致第一個(gè)氣動(dòng)力峰值的出現(xiàn)；動(dòng)態(tài)失速渦誘導(dǎo)形成后緣渦，在后緣渦的作用下，使得動(dòng)態(tài)失速渦向翼型表面靠攏，并重新附著于翼型上表面，從而導(dǎo)致翼型氣動(dòng)力二次峰值的出現(xiàn)。

（2）翼型厚度增加、彎度位置前移以及一定范圍內(nèi)彎度的增加，會(huì)推遲動(dòng)態(tài)失速渦和后緣渦的形成，并增加動(dòng)態(tài)失速渦和后緣渦強(qiáng)度，從而使得氣動(dòng)力二次峰值推遲，二次峰值增量增加。而當(dāng)翼型彎度較大時(shí)，翼型的失速方式從前緣失速變?yōu)楹缶壥佟Ｅc前緣失速情況相比，后緣失速情況下形成的動(dòng)態(tài)失速渦和后緣渦的強(qiáng)度較小，因此氣動(dòng)力系數(shù)二次峰值增量較小。