基于特征系數靈敏度的魯棒極點配置＊

蔣小平,陳曉飛

(中國礦業大學(北京)機電與信息工程學院，北京 100083)

1 引言

魯棒性原是統計學中的一個專門術語，20 世紀70年代初開始在控制理論的研究中流行起來，用以表征控制系統對特性或參數攝動的不敏感性[1]。由于魯棒性這一性質，隨著在工程中對控制系統的精度以及穩定性的要求逐漸嚴格，魯棒控制便早已成為控制屆的重要問題，在控制理論課程中的地位也是愈來愈重要。極點配置作為改善線性時不變系統性能指標的常用技術方法之一，其魯棒極點配置的相關問題研究相應有著很重要的教學和研究意義。關于魯棒極點配置問題的研究，為了方便魯棒系統設計，要引入了一些魯棒指標，進而提出了各種最優魯棒極點配置方法。但遺憾的是，大多指標較難計算，且最優魯棒極點配置方法具有一定的局限性。考慮特征系數靈敏度計算簡單，本文把加權后的特征系數靈敏度作為魯棒指標，目標函數的極小化采用標準的具有二次收斂性質的參數最優化方法。并且本著控制課程教學的目的，對原理進行詳細講解，設計實例驗證算法的可行性。

2 線性系統

線性系統通常因某些不確定因素而無法精確建立，這就導致了系統的不確定性[2]。

具有不確定參數的線性時不變多變量系統可用下列狀態方程描述[3-5]：

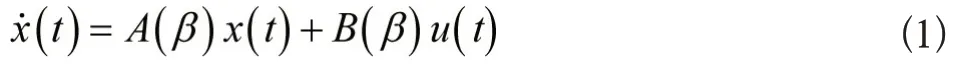
式中，x(t)∈Rn為狀態向量；u(t)∈Rm為輸入向量；β∈D∈Rr為不確定性參數向量(D 為β 的取值區域)，其名義值為β0；A(β)∈Rn×n，B(β)∈Rn×m是依賴于不確定性參數向量β 的系統矩陣和控制矩陣。……