基于干預模型的酒駕違法查處與事故關聯分析＊

許卉瑩 瞿偉斌 公安部交通管理科學研究所

引言

世界衛生組織的調查顯示：酒后駕駛是車禍致人死亡的一個主要原因。在多數國家，酒駕是導致交通事故的首要原因，例如美國、南非等。在我國目前仍處于酒駕事故的高發期，起數、死亡人數總量比較大，造成了巨大的生命財產損失。據統計，每年酒駕肇事事故超過萬起，占到事故總數的6%。近年來，隨著查處執法力度的進一步加大，酒駕違法行為大幅減少，酒駕事故也在相應減少。2020年因受疫情影響，酒駕行為的查處稍有減弱，與此相對的，酒駕醉駕事故有所抬頭。從近年酒駕違法和事故數據可以看出，酒駕查處力度對于酒駕事故的發生有比較明顯的影響，可以通過分析兩者之間的關聯關系，更加客觀的了解交通事故的發生機理，從而為交管部門的管理決策提供數據依據和技術支撐。

一、酒駕違法與事故相關性分析

在酒駕的情況下，駕駛人對外界的反應能力及控制能力下降，導致運動反射神經遲鈍、易疲勞等，容易發生事故。而交警查處酒駕，一方面使得飲酒的駕駛人無法繼續駕駛，避免事故發生；另一方面會對駕駛人酒駕起到震懾作用，從而達到預防酒駕事故的效果。可以認為，酒駕查處力度和酒駕事故發生之間存在一定的相關關系。

（一）數據集說明

本文以江蘇省某城市2018年5月至2020年4月間酒駕違法查處數據與酒駕交通事故數據為例，具體分析其相關性。

從酒駕違法查處情況看，大致分為四個階段：2018年5月至2019年5月，較為平穩的階段；2019年6月至12月，因受查處酒駕專項行動影響，酒駕查處數逐月遞增，至9月達到峰值，然后稍有回落；2020年1月至2月，因受疫情影響，酒駕違法查處數處于歷年最低水平；2020年3月至5月，酒駕違法查處數快速回升，恢復至2019年平均水平。而相對應的，事故數據也分為4個階段，基本與違法查處時段吻合：2018年5月至2019年5月是上升階段；2019年6月至2019年9月是下降階段；2019年10月至2020年1月，酒駕事故數有所回升；2020年1月至2020年5月，該階段酒駕事故數先大幅下降后快速上升，如圖1所示。

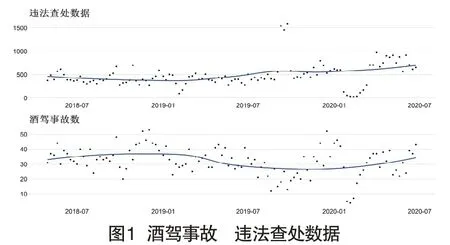
（二）相關性分析

相關系數是研究變量之間線性相關程度的量，以兩變量與各自平均值的離差為基礎，通過兩個離差相乘來反映兩變量之間相關程度。本文采用皮爾遜相關系數法，公式如下：

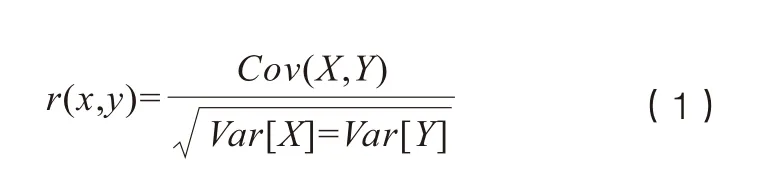
其中，X是酒駕違法查處數，Y事故數。為方便分析，以一周作為時間間隔，將酒駕事故與違法查處數分段計數。以自2018年5月以來每周的酒駕違法查處與酒駕事故數據，計算其相關系數，結果為-0.38，說明兩者呈較明顯的負相關性。

二、時間序列干預模型建立

時間序列模型可以用于尋找序列值之間相關關系的統計規律，并構建適當的數學模型來描述這種規律，進而利用這個擬合模型來預測序列未來的走勢。酒駕事故數據存在明顯趨勢，符合某種統計規律，可以用時間序列模型來進行預測。而時間序列經常會受到特殊事件及態勢的影響，一般稱這類外部事件為干預。從上文的相關系數結果來看，酒駕違法查處力度與酒駕事故發生趨勢之間具有相關性。提升酒駕違法查處力度，對于酒駕事故的發生來說可以認為是一種特殊干預，可以建立干預分析模型，從定量分析的角度來評估酒駕違法查處力度對酒駕事故的具體影響。具體思路：

（1）利用受干預影響之前的事故數據，建立一個時間序列模型，并利用此模型進行外推預測，得到假設不受干預影響情況下的預測值；

（2）分析預測值與受干預影響的實際值，識別干預效應的形式，確定干預效應函數的參數，構建干預分析時間序列模型；

（3）通過干預分析模型進行事故趨勢預測。

（一）酒駕事故受干預影響前的時間序列模型

利用受干預影響之前的酒駕事故數據，建立時間序列模型，預測酒駕事故的發生情況。具體思路：首先識別酒駕事故是否為平穩時間序列，若不為平穩時間序列，則需要對原始序列做平穩化處理；然后再建立差分自回歸滑動平均(ARIMA)模型。

1. 數據預處理

數據預處理，就是在建模之前先對原始數據做平穩化處理、白噪聲檢驗和離群值檢驗，使得處理后的數據滿足ARMA模型的假設，為建模做好準備工作。

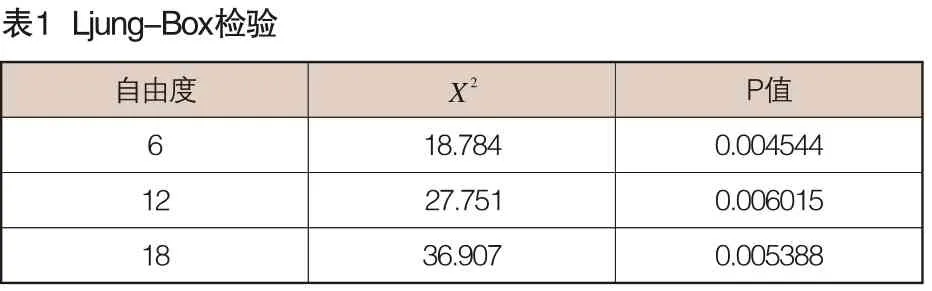
首先檢驗序列{Xt}的平穩性。對原始序列做adf檢驗，當滯后階數為2時，P值就大于0.1，所以有理由相信序列{Xt} 不為平穩序列，屬于非平穩時間序列。然后對序列進行平穩化。使用一階差分運算后得到一個新序列{Yt} ,Yt=Xt-Xt-1，序列代表每周的環比變化量。在建模之前，還需檢驗序列是否為白噪聲序列。再采用常用的Ljung-Box檢驗法對新序列{Yt}做隨機性檢驗，檢驗的結果詳見表1。

?

這說明，在0.01的顯著水平下，序列{Yt}不為純隨機性序列，即每月的環比變化序列{Yt}是有規律可循的，可以對其建立ARMA模型。

2. 模型識別

模型識別，就是對于給定的時間序列，選取適當的模型階數p,d,q。在前面預處理過程中，通過一階差分，將非平穩序列{Xt} 轉換為平穩序列{Yt}。因此選定差分階數d=1。對于平穩序列，識別p,q的主要根據是序列的自相關函數（ACF）和偏自相關函數（PACF）的特征。若序列的偏自相關函數在滯后階以后截尾，而且它的自相關函數拖尾，則可判斷此序列是ARMA(p,0)序列。若序列的自相關函數在滯后q階以后截尾，而且它的偏自相關函數拖尾，則可判斷此序列是ARMA(0,q)序列。若序列的自相關函數、偏相關函數都呈拖尾形態，則此序列是ARMA序列。根據序列{Yt}的樣本自相關函數和偏相關函數，初步選定模型的階數為p=1,q=1。

3. 參數估計

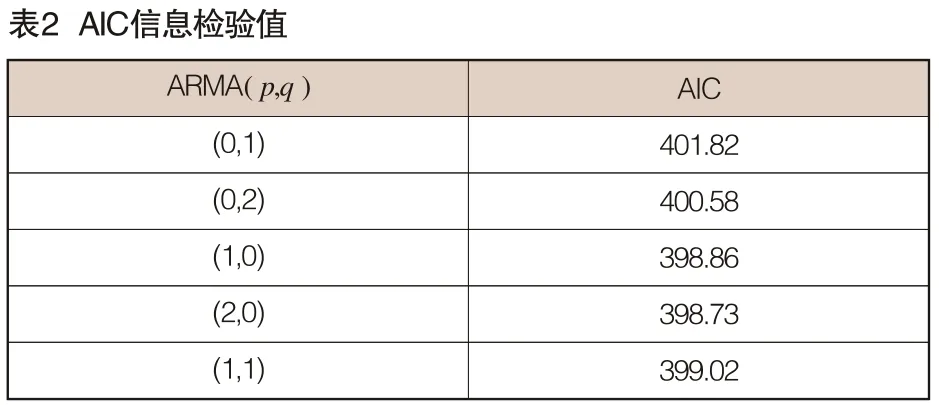
在選定模型階數之后，對已識別模型中的若干參數進行估計計算。為更準確的選擇模型，采用模型的AIC信息檢驗值進行篩選，根據最小信息量準則選取最優模型，詳見表2。

?

將模型修正為ARMA(0,1)，得到序列{Yt}的ARMA （2.0）模型，該模型的所有系數估計值都比較顯著。

4. 模型診斷

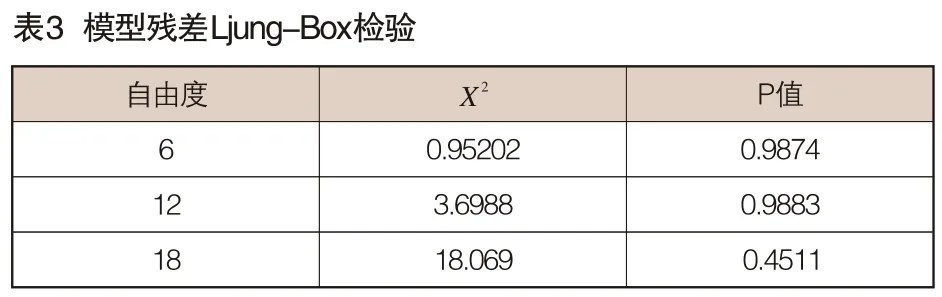
模型的顯著性檢驗即檢驗殘差序列是否為白噪聲序列。一個好的擬合模型應該能夠提取觀察值序列中幾乎所有的樣本相關信息，即殘差序列應該為白噪聲序列。反之，如果殘差序列為非白噪聲序列，那就意味著殘差序列中還殘留著相關信息未被提取，這就說明擬合模型不夠有效。令Xt代表模型對觀測值Xt的 估計值（擬合值），定義et=Xt-Xt為擬合殘差。采用Ljung-Box檢驗法對殘差序列在自由度分別為6、12、18的情況下做三次白噪聲檢驗，檢驗結果均顯著，可以認為序列{et}為白噪聲序列，模型通過模型顯著性檢驗，詳見表3。

?

（二）時間序列干預分析模型

1. 模型說明

時間序列干預分析模型可以表示為：

其中，mt代 表干預效應項，它是干預變量的函數，Nt為 ARIMA模型，代表著未受干預影響的基礎時間序列。干預變量有多種形式：第一種是持續性的干預變量，可以用階躍函數式（3）表示；第二種是短暫性的干預變量，用單位脈沖函數式（4）表示。

其中，T為干預時間。干預效應對于模型的影響體現在mt的變化上。當發生持續性干預時，干預效應項可記為m=ωS T，其表示在T時刻發生的干預在經過d個時間單位延遲后干預作用顯現；同理當短暫性干預發生時，干預效應項可記為表示T時刻發生的干預在該時刻瞬間對模型產生了ω的影響。

干預效應除了有一定的延遲，同時還可能與自身有一定的相關性，或者干預的強弱也有可能隨時間而變化，所以在實際問題中需要將以上基本形式結合起來，對干預效應建模。

2. 建模過程描述

酒駕違法查處行動是非連續且有梯度的干擾，不像簡單持續性干擾一樣一次行動便始終維持，也不像短暫性干擾只對序列作用一次。在假定酒駕人群比例在短時間內不會改變的前提下，酒駕查處力度與酒駕違法查處數呈正相關。酒駕違法查處數越多，象征著酒駕查處力度越大。一段時間內酒駕查處力度的直接體現就是酒駕違法的查處數量。將TT時間的酒駕查處力度記為ωT， 干預模型如下：

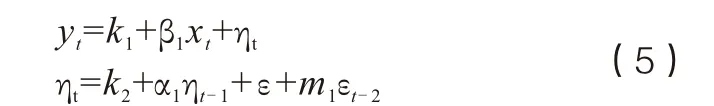
其中，xt為 時間序列的干預項，ηt為去除干預項的ARIMA時間序列模型。

3. 模型診斷

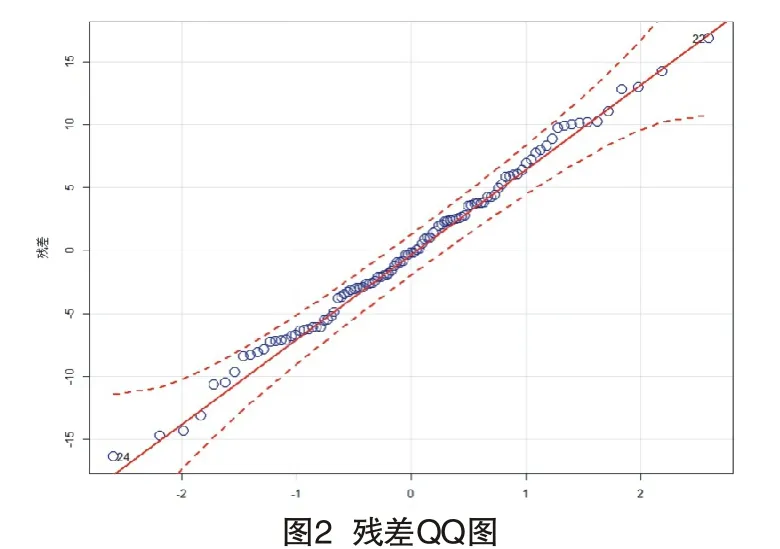
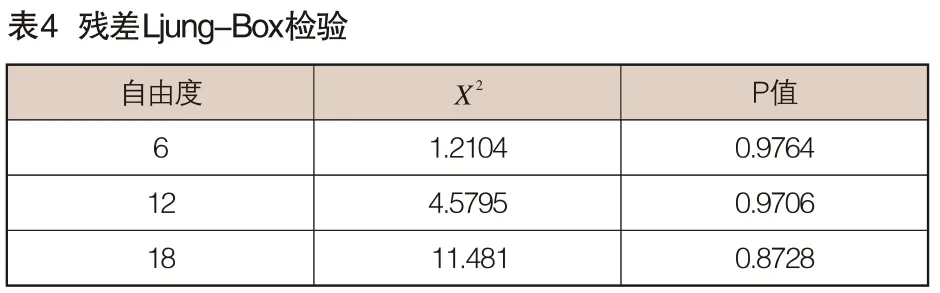
為診斷模型的有效性，需要對模型殘差進行檢驗，通過分析其是否服從正態分布以及是否為白噪聲來判斷模型是否顯著。如圖2所示，其殘差服從正態分布。采用LjungBox 檢驗法對上述模型的殘差序列{et}做模型顯著性檢驗，檢驗的結果詳見表4，殘差序列為白噪聲序列的可能性大于99%，模型通過顯著性檢驗。

?

三、模型應用

（一）酒駕事故受干預影響前的時間序列模型應用

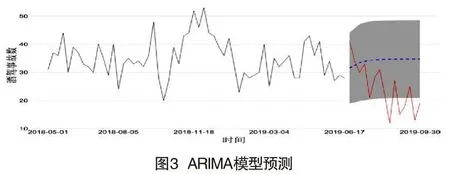
從前文數據集的時間特征可知，2019年6月至12月是查處酒駕專項行動影響時段。因此筆者采用2018年5月-2019年5月間酒駕違法查處數據與酒駕交通事故數據，建立受干預影響之前的時間序列模型，并預測2019年6月至2019年9月的酒駕事故數據。預測結果如圖3所示，其中實線為實際每周發生的酒駕事故數，虛線為模型預測的酒駕事故數，灰色區域為95%置信區間。根據模型結果來看，在未受干預影響的情況下，序列呈現一個平穩波動的趨勢，當前一周的數據與前一周相關，與更早的歷史數據關系不大。模型預測2019年6月至9月每周的酒駕事故數應在35附近波動，其95%的置信區間為[21,48]。

（二）干預分析模型應用

將受干預影響前的時間序列模型的預測結果與實際數據進行對比發現，酒駕事故數量自2019年6月以來呈現下降趨勢，并且持續位于預測值置信區間以外。可以認為因2019年6月查處酒駕專項行動，酒駕查處力度加大，對酒駕事故數產生了干預影響。接下來將通過干預分析模型來分析具體干預影響的程度。

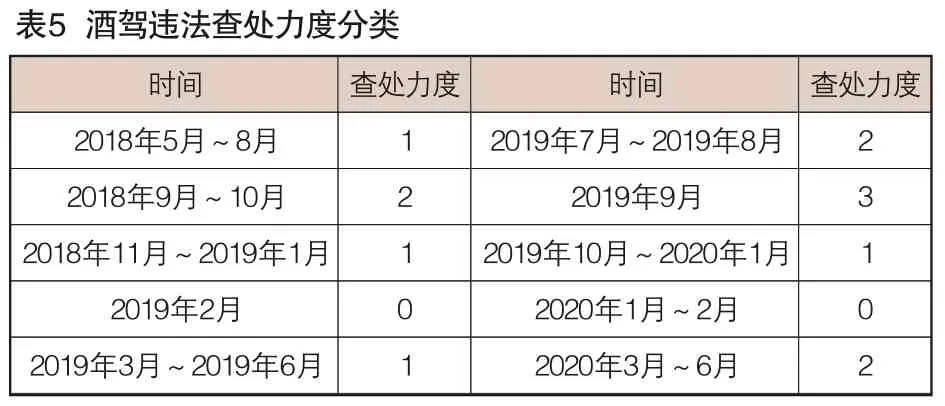
首先利用kmeans方法將某城市酒駕違法查處數量進行劃分，酒駕違法查處數量最高時段的查處力度標記為3，次高的時段標記為2，以此類推，最少的時段的查處力度標記為0。具體劃分結果詳見表5。

?

然后，基于現有數據集進行參數估計，模型的數學表達式如下：

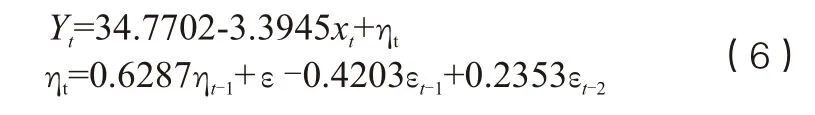
模型的擬合結果如圖4所示。其中紅色實線為模型的擬合結果，兩條藍色虛線間的范圍為模型置信區間。可以看到，在置信區間下，對于數據的擬合較為符合。

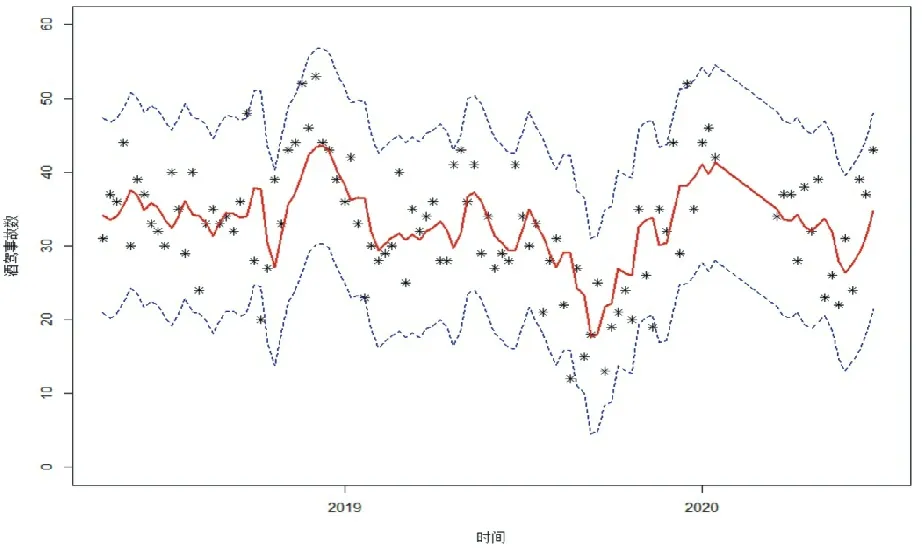
圖4 干預模型擬合

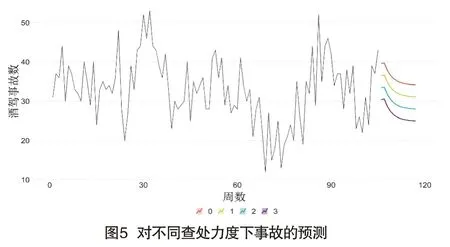
通過模型對2020年6月以后的三個月數據進行預測，結果如圖5所示，當保持違法查處力度為0時，酒駕事故將維持原有水平；當查處力度為1時，酒駕事故相比原有水平下降8.57%；當違法查處力度為2時，酒駕事故相比原有水平下降17.14%；當違法查處力度為3時，酒駕事故相比原有水平下降28.57%。以上分析說明酒駕查處力度對酒駕事故發生有干預影響。在酒駕查處力度加大時，酒駕事故有下降的趨勢。

四、結語

通過建立干預分析模型發現，酒駕違法查處力度對于事故發生的干預效用明顯。干預模型能夠用來定量分析交通違法行為查處力度對交通事故的干預影響，明確優化執勤執法排班、調整執法力度對事故的干預影響程度，進而可以應用于交通事故預防效果評估、事故趨勢預測，為有效預防酒駕事故提供技術支撐。

研究重點在干預模型的建立與分析，而在酒駕違法與酒駕事故數據相關性方面，僅進行了初步探討，在未來需要進行深入研究。