采用模糊k核多粒度分解機制的高效社區發現
李宏平,劉 群
(重慶郵電大學 計算機科學與技術學院,重慶 400000)
0 引 言
社區結構的發現對于理解復雜網絡中的結構有重要作用[1-4]。Newman算法[5]在傳統算法的基礎上大幅度降低了運算時間,使得社區發現不再局限于小規模網絡。louvain算法[6]進一步優化了大規模網絡圖上的社區發現運算時間。LPA算法[7]通過少量預定義社區標簽預測其余大部分未定義節點的標簽,實現對大規模網絡的快速社區劃分。Walktrap算法[8]采用計算節點間的相似性的方式高效地捕捉各種規模網絡的社區結構。貝葉斯模塊選擇算法[9]能高效、可解釋地計算出節點的社區分配以及社區的最佳數量。雖然上述方法對時間復雜度有所降低,但是它們的計算時間與節點數量的關系密切相關,仍然需要花費較多的計算時間,尤其對于規模較大的網絡,問題更加顯著。可見,如何在減少社區發現算法運算時間的同時保證社區發現的精確度是社區發現領域還存在的一個問題。
針對上述問題,本文提出了一種基于模糊k-core的社區發現算法,首先使用k-core子圖代表整個社區結構的分布,以減少社區劃分的運算時間;在傳統k-core分解的基礎上運用模糊理論的隸屬度函數得到模糊k-core子圖,最大可能地保留高重要性節點,對模糊k-core子圖進行社區劃分,并將劃分結果合理有效地擴散到其余節點,以保證社區發現準確度。實驗結果表明,本算法在不同規模的真實網絡數據集上與以上大部分算法相比,在減少運算時間的同時保證了社區劃分的準確性,體現出了較強的綜合性能。
1 相關知識
1.1 k-core分解
k-core分解可以區分不同節點的結構重要性并保留節點的鄰域關系。該方法遞歸刪除度數小于k的節點,直到所有其余頂點的度數都大于或等于k。k-core分解是一種基于節點的度,以提取核心節點集為目標的算法。
定義1 圖的凝聚度:表示一個圖網絡中節點與節點之間聯系的緊密程度,通常由連通度和直徑這兩個度量指標進行衡量,其中連通度是將一個連通圖轉變為非連通圖所需要刪除節點數的最小值,直徑是任意兩節點之間最短路徑的最大值。圖的凝聚度與連通度成正比,與直徑成反比。
定義2 k-core:存在一個圖G(V,E),V表示節點集,E表示節點間的邊集,d(v)表示節點v的度數。假設H是G的一個子圖,δ(H)表示H子圖的最小度,H中的每一個節點都至少有δ(H)個鄰接點;若H是G的一個引導子圖且δ(H)≥k,不包含于其余任意一個最小度大于等于k的引導子圖,則H子圖為圖G的一個k-core,用KG(V,E)表示[10]。
定義3 k-remainder:由k-core得到(k+1)-core的修剪過程中被刪除的節點集[10]。Rk表示節點集,rk表示相應的節點數。
圖1用不同的空心圓(分別為J1,J2,J3)顯示k值分別取1、2、3時的k-core。由于任意節點v的d(v)≥1,所以每個節點都屬于1-core(由J1包圍),R0為空集,r0=0。遞歸刪除d(v)<2的節點(圓形)后,其它節點d(v)≥2,形成2-core(由J2包圍),同時被刪除的所有節點構成1-remainder,由R1表示,R1=15。進一步的修剪可以識別由三角形節點集所組成的3-core(由J3包圍),同時在修剪過程中被刪除的所有菱形節點構成2-remainder,由R2表示,R2=5。此時,如果繼續修剪,在從3-core中得到4-core的過程中,所有三角形節點都將被刪除,所以圖1的kmax=3,且三角形節點構成3-remainder,由R3表示,R3=9。從圖中可以明顯看出,如果一個節點屬于3-core,則它也屬于2-core和1-core。根據以上例證可以看出,處于核心位置的節點往往具有較高的k值。
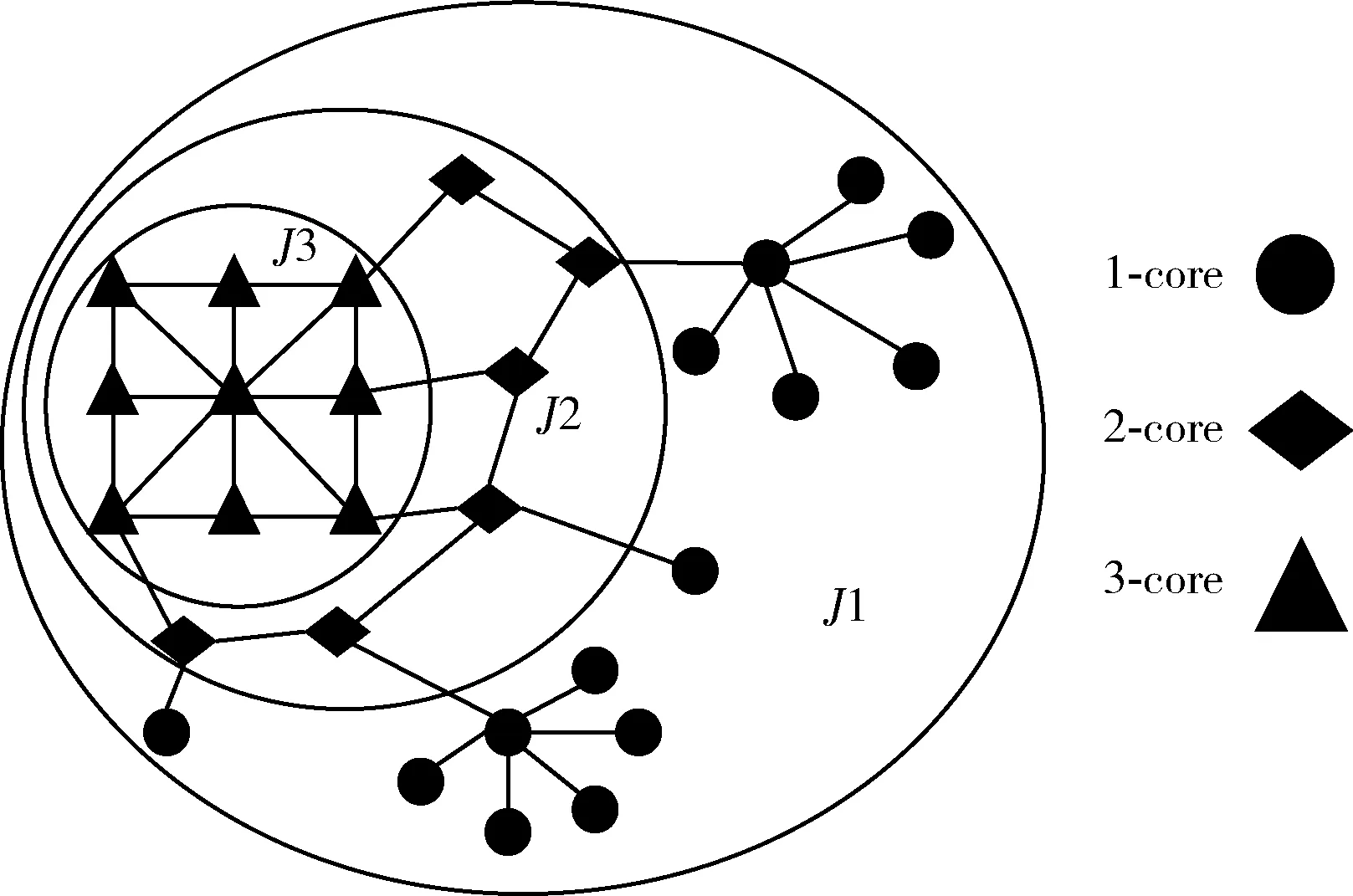
圖1 k-core分解
定義4 核塌縮序列:CCS(core collpase sequences)[10]可以直觀展現一個圖網絡的凝聚度分布,表示為 {Rk/|V(G)|},其中|V(G)|為圖G的總節點數,k值上限為圖G所包含的最小k-core的k值。以圖1為例,整個圖網絡的節點總數為30,其中R0=0,R1=15,R2=5,R3=9,則該網絡的CCS為 {0,1/2,1/6,3/10}。
k-core分解可以將網絡劃分為凝聚度不同的子網。k值越大,子網的凝聚度就越高。CCS直觀地展示了凝聚度從弱到強的子網在整個網絡的規模占比,反應了整個網絡圖的節點分布結構。
本文在傳統k-core分解的基礎上采用模糊k-core分解的方法,使更多的高重要性節點得以保留在k-core子圖中。
1.2 傳統模糊理論
模糊集理論對經典集合理論的擴展,最主要的貢獻在于引入了集合中元素對該集合的隸屬度[11]。
定義5 隸屬度:主要通過隸屬函數A(x)表示。用取值于區間[0,1]的隸屬度函數A(x)表征x∈A的程度高低。A(x)越接近于1,表示x∈A的程度越高,A(x)越接近于0表示x∈A的程度越低。
“粒度”源于模糊集理論[12],對于粒度的計算是一種來自不同層次,不同視角的思維方式[13,14]。k-core中也存在粒度,其將原始網絡劃分為多個子網絡,每個具有不同k值的子網都代表一個粒度層。k值越大,子網中的節點數越少,子網中的節點重要性越高。
本文通過使用模糊k-core分解,將原網絡劃分為多粒度網絡,相較于傳統k-core分解的嚴格劃分,此多粒度網絡能更大程度地保留高重要性節點,更能從局部體現整個網絡的社區分布。
2 基于模糊k-core的社區發現算法設計
2.1 問題描述
整個算法包括模糊k-core分解,子圖社區劃分和社區標簽擴散3個步驟。首先對目標圖網絡進行模糊k-core分解,得到整個網絡的核心節點集(即模糊k-core子圖);之后對核心節點集進行社區劃分,使每個節點得到社區標簽;最后將社區標簽擴散到網絡中其余所有節點,完成整個網絡的社區劃分。大致流程如圖2所示。
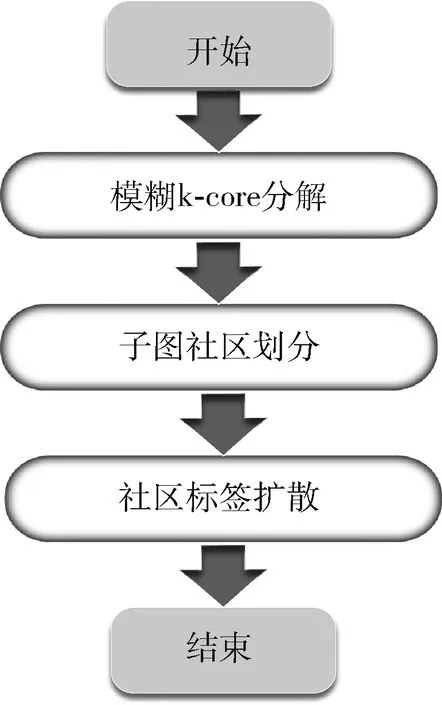
圖2 算法流程
2.2 模糊k-core分解
盡管k-core表示的概念很明確,每個節點與集合的隸屬關系也很清楚,可以很好地將重要性不同的節點劃分為不同的網絡層,但是k-core分解在捕獲節點重要性方面存在一些問題,即其遞歸修剪過程過于嚴格,導致一些重要性高的節點沒有保留在k-core網絡中。由于并非所有概念都適合進行清晰的劃分,為了捕獲更多的高重要性節點,本文提出基于k-core分解的模糊劃分。
如圖3所示,要獲得2-core子圖,就必須在經過遞歸修剪過后,所有節點的度數都大于或等于2。圖3(a)描述了從1-core到2-core的第一次修剪過程。圖3(b)為經過完整遞歸修剪過后的2-core子圖。在原始網絡G中,d(v1)=6,d(v2)=7,兩個節點的度數在圖G中屬于較大范疇,表明節點v1和v2在網絡中是高重要性節點。但根據k-core分解的定義,節點v1和v2在2-core的生成過程中將被刪除。為了更好地篩選出高重要性節點,需要在k-core分解算法基礎上,采用模糊函數對節點進行二次判斷。
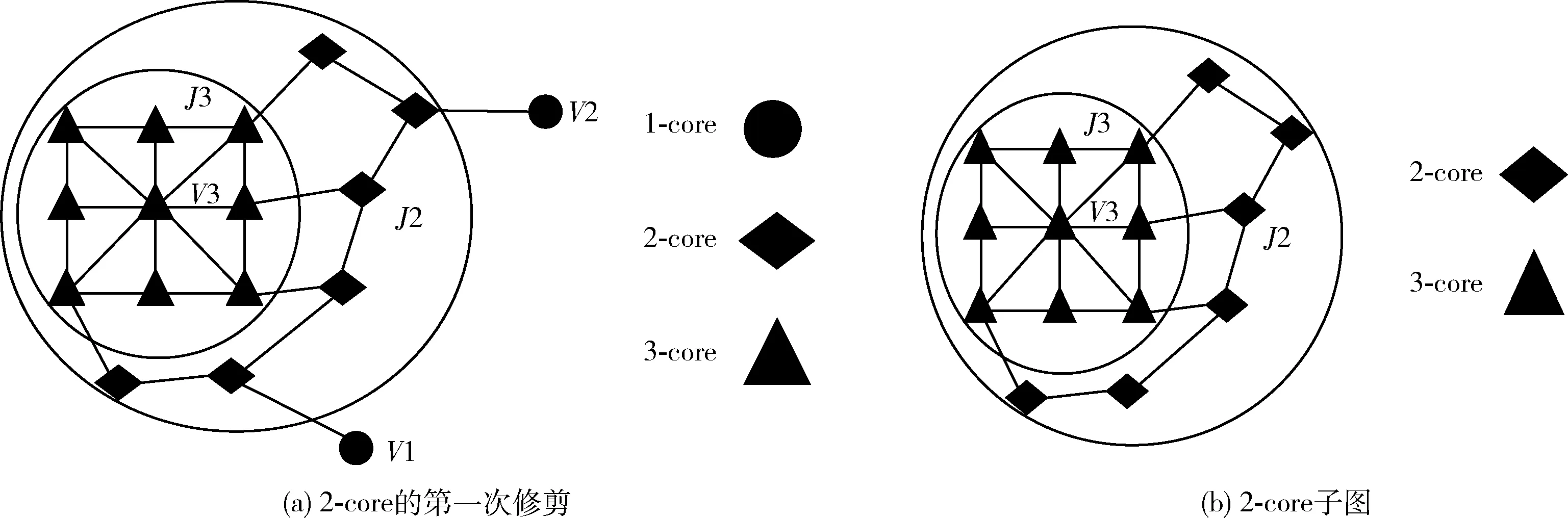
圖3 從1-core到2-core的分解過程
盡管k-core表示的概念很明確,每個節點與集合的隸屬關系也很清楚,可以很好地將重要性不同的節點劃分為不同的網絡層,但是k-core分解在捕獲節點重要性方面存在一些問題,即其遞歸修剪過程過于嚴格,導致一些重要性高的節點沒有保留在k-core網絡中。由于并非所有概念都適合進行清晰的劃分,為了捕獲更多的高重要性節點,本文提出基于k-core分解的模糊劃分。
模糊k-core分解關于隸屬度的模糊函數表示如下
d(v)d=d(v)-d(v)r
(1)
(2)
節點v為圖G中任意節點,d(v)表示節點v在完整網絡中的度數,d(v)r表示節點v在嚴格k-core分解過程中將會被刪除時的度數,d(v)d表示節點v原始度數與被k-core分解刪除時的度數之差,A(v)k為節點v的隸屬度,表示其隸屬于k-core的概率,其中b=2k。當A(v)k≥0.5時,節點v屬于k-core。當k=3時,將節點v保留在k-core子圖的條件是d(v)d≥5;當k=5時,節點v保留在k-core子圖的條件是d(v)d≥8。與嚴格的k-core分解修剪條件相比,此模糊函數能保留更多的高重要性節點,k值越大時,效果越明顯。并且不會出現隸屬度值突增或者突減的情況,保證了不同k值下模糊匹配的平滑性。
若在k-core分解的基礎上附加模糊函數,就會對不同粒度層的k-core子圖進行重新劃分,代表凝聚度分布的核塌縮序列也會相應改變。如圖2和圖3所示,根據k-core分解的節點分配原則,節點v1和v2屬于R1,CCS為 {0,1/2,1/6,3/10}。根據模糊k-core分解的隸屬度函數對v1和v2進行二次劃分后,節點v1被劃分到3-core,屬于R3;節點v2被劃分到4-core,屬于R4,并且其它節點同樣也會被隸屬度函數進行重新劃分,比如節點v3原屬于3-core,被二次劃分到5-core,屬于R5。最終得到圖G的模糊子圖FKG(V,E),其CCS為 {0,13/30,1/6,3/10,1/30,1/30},可以看出,隨著模糊k-core分解的加入,CCS也能更詳細準確地描述一個圖網絡的粒度層更豐富的凝聚度分布。
模糊k-core分解的算法過程如下:
算法1:模糊k-core分解
輸入:圖G(V,E)
輸出:模糊k-core子圖FKG(V,E)
(1)讀取數據集圖網絡G(V,E);
(2) 對G(V,E)進行模糊k-core分解;
(3)fori=1tokdo
(4)foreach nodevinVdo
(5)ifd(v)r≥ithen
(6) 保留該節點
(7)else
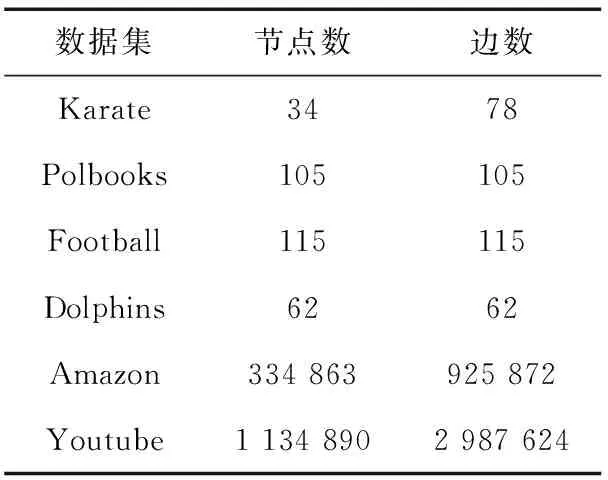
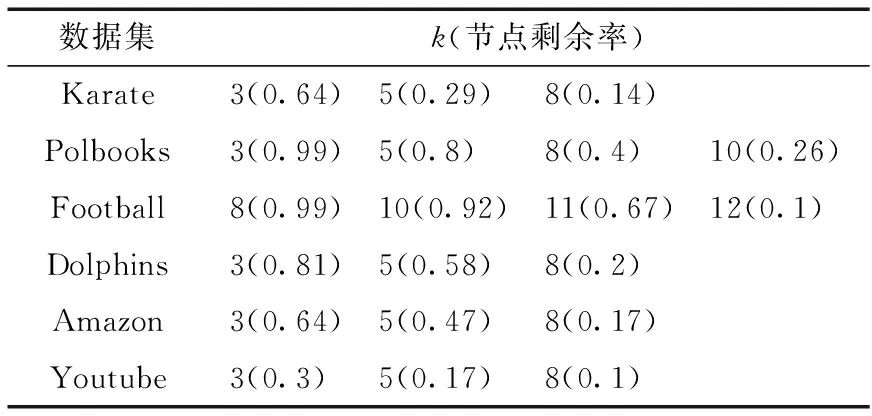
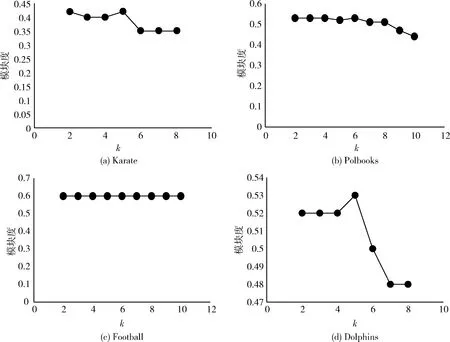
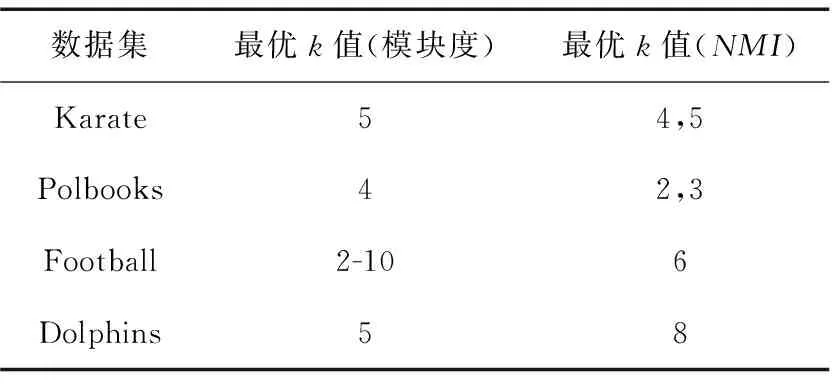
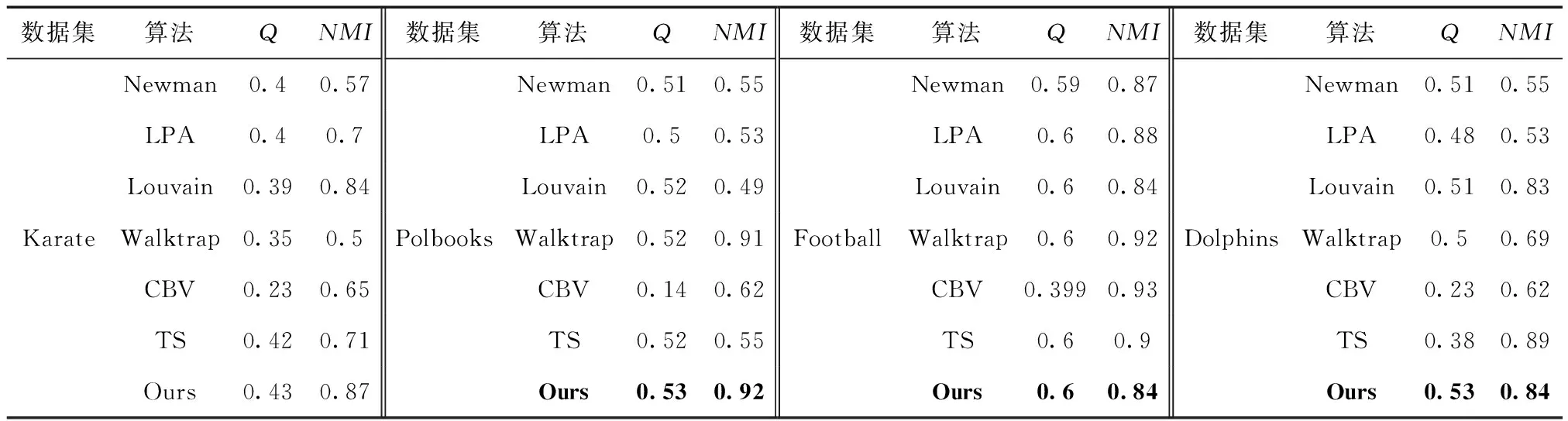
(8)ifd(v) (9) 刪除該節點及其鄰邊//即該節點A(v)k=0 (10)else (11)ifd(v)d (13) 保留該節點 (14)else (15) 刪除該節點及其鄰邊 (16)else (17) 保留該節點 //即該節點A(v)k=1 (18)endfor (19)endfor 存在一個圖G(V,E),聚類算法在圖中找尋一種節點劃分方案,并為每個節點分配一個社區標簽,擁有相同標簽的節點共同形成一個集群,使得節點集被分割成n個不同的小集群C={C1,C2,C3,C4,……},其中Cj?V且Cj≠?(i=1,2,3,4,……,n),滿足Ci∩Cj=?(j=1,2,3,4,……,n且i≠j),集合C被稱為圖G的一個社區結構[15]。 模塊度Q是一種表示網絡社區結構強度的度量值,其取值范圍為[-1,1],常用于衡量一個社區劃分結果的優劣[5]。一個理想化的社區劃分,是社區內部節點間相似度盡可能的高,同時社區外部節點間的相異度盡可能高,此時模塊度的值就越高。也就是說,社區劃分的質量越高對應的模塊度Q越大[5] (3) Ai,j為網絡對應鄰接矩陣中的一個元素,表示節點i與j之間的邊(可能存在,也可能不存在) (4) ci和cj分別是節點i和節點j所在的兩個社區,如果i和j在一個社區,即δ(ci,cj)則為1,否則為0。m表示網絡中所有邊的數量,ki表示所有與節點i相連的邊的數量(即節點i的度數) ki=∑j(Ai,j) (5) 模塊度不僅可以用于衡量社區發現的優劣,還可以作為目標函數被優化[16]。 圖G的模糊k-core子圖FKG(V,E)代表整個圖中重要性最高的節點集,對FKG(V,E)進行局部劃分后再將標簽擴散到整個圖網絡,可以顯著降低運算時間的同時保留或者提升社區劃分質量。在本文提出的基于模糊k-core的社區發現算法中,對模糊k-core子圖進行聚類的算法過程如下: 算法2:子圖社區劃分 輸入:模糊k-core子圖FKG(V,E) 輸出:社區結構Cfk={C1,C2,C3,C4,……} (1) 初始化: 為FKG(V,E)中的每個節點分配社區標簽; (2)do (3) 計算社區結構的模塊度Ql; (4) 將每個節點劃分到其鄰接點所在社區,并計算模塊度QR (5) ΔQ=QR-Ql (6)While(ΔQ>0)do (7) 保留當前社區結構 (8) 重復步驟(3) (9)end (10) 將同一社區節點集簡化為單個節點 (11)While(ΔQ>0) 由于模糊k-core子圖是整個圖網絡中重要性最高的節點集,這個節點集能夠代表整個圖網絡的社區結構分布,即其余非模糊k-core子圖的所有節點都依附FKG(V,E)并隸屬于其社區劃分,所以可以根據模糊k-core子圖的標簽分配結果推斷非FKG(V,E)節點的社區標簽,從而完善并優化整個圖的社區結構。 首先,根據每個無標簽節點的帶標簽鄰接點數量,對所有無標簽節點進行降序排列。然后,按序列依次遍歷每個無標簽節點,計算其鄰接點集中各標簽的占比,為該節點分配占比最高的標簽,直到所有節點都被分配到標簽為止,完成整個圖網絡的社區發現。算法過程如下: 算法3:社區標簽擴散 輸入:FKG(V,E)的社區結構Cfk={Cfk1,Cfk2,Cfk3,Cfk4,…,Cfkn} 輸出:全網絡社區結構C={C1,C2,C3,C4,……,Cn} (1)處理非FKG(V,E)節點集Vr; (2)foreach nodevinVrdo (3) 計算節點v帶標簽的鄰接點數量 (4)endfor (5) 對Vr中節點進行降序排列,得到節點序列L (6)fori=1tondo//n為L中的節點數 (7) 計算節點vi的鄰接點集中各標簽占比 (8) 為節點vi分配占比最高的標簽 (9)endfor 本節通過在6個社會網絡數據集上的實驗來驗證基于模糊k-core的社區發現算法的有效性。第3.1節為實驗準備部分,介紹了實驗環境。實驗中使用的各類型的數據集,對比算法。模糊k-core分解的重要參數設置以及實驗結果評價標準。本文將實驗按照使用到的數據集規模大小分為兩部分,基于小數據集的實驗將在第3.2節中詳細介紹,基于大數據集的實驗將在第3.3節中詳細介紹。 實驗的硬件環境為:Intel(R)Core(TM)i7-9700 @3.3 GHZ,RAM:16 GB,軟件環境為:Windows 10操作系統,編程語言為:Python。 本文選取了6個在復雜網絡領域常用的帶基準的真實網絡數據集對算法的有效性和準確性進行驗證,見表1。這6個數據集都是無方向,無權值網絡,其中4個小數據集包括: Karate網絡[17]是Zachary的一個空手道俱樂部的社交網絡,由34個節點和78條邊組成。節點表示該俱樂部成員,邊表示兩個節點成員是否在俱樂部之外有聯系。 Polbooks網絡[18]是美國的政治書籍所構成的網絡,由105個節點和105條邊組成。節點表示Amazon.com所賣出的美國政治書籍,邊表示兩本書籍在購買傾向上是相似的。 Football網絡[5]是美國職業足球隊所構成的網絡,由115個節點和115條邊組成。節點表示每一個職業足球代表隊,邊表示兩個節點所代表的球隊至少進行了一次比賽。 Dolphins網絡[19]是一些在一起生活的寬吻海豚所構成的網絡,由62個節點和62條邊組成。節點代表每一只不同的海豚,邊表示兩個節點所代表的海豚經常一起活動。 另外還包括兩個相對較大的數據集,用于著重驗證本文算法在運算時間上的優越性: Amazon網絡[20]是由Amazon在線商城里所出售的商品所構成的網絡,由334 863個節點和925 872條邊組成。節點表示每一個出售的商品,邊表示兩個節點所代表的商品經常被一起購買。 Youtube網絡[20]是由一個視頻分享網站所包含的社交網絡,由1 134 890個節點和2 987 624條邊組成。節點表示網站中每一個注冊用戶,邊表示兩個節點所代表的用戶聯系緊密。 各數據集的規模見表1。 表1 實驗數據集 實驗選取了一共6種算法,包括Newman,LPA,louvain,Walktrap等經典算法以及近期的CBV[21]和TS[22]算法,與本文所提出的基于模糊k-core的社區發現算法在相同的4個小數據集上進行實驗對比。其中,Newman算法是基于貪心算法的快速社區發現算法,LPA算法是基于節點標簽的全局社區發現算法,louvain算法是以模塊度優化為目標的全局社區發現算法,Walktrap是基于節點間距離的社區發現算法。 本文實驗用于驗證算法的指標包括模塊度Q,NMI以及運算時間。 由于實驗所使用的數據集均是帶有基準信息的真實數據集,所以除了模塊度,本文也使用NMI[23]表示算法對網絡的劃分結果與網絡的真實劃分之間的差異,其取值范圍為[0,1],定義如下 (6) CA為真實劃分的社區數量,CB為算法所得劃分的社區數量,Nij表示在算法所劃分的社區j中屬于真實社區i的節點數量,Ni.表示矩陣Nij的第i行元素之和,而N.j則是第j列元素之和。算法所得劃分與真實社區越相近,NMI值就越大,當算法所得劃分與真實社區完全一致時,NMI(A,B)等于1。 在本文所提出的基于模糊k-core的社區發現算法中,模糊k-core剪枝過程中k值的取值對于實驗結果有著重要影響。算法的核心在于經過模糊k-core修剪后所得到核心子圖。模糊k-core子圖的規模隨著k值的增加而減小,即k值越大,算法所得到的子圖就越趨近網絡核心,越有利于挖掘出網絡的核心節點集,在進行局部社區劃分時所需要的運算時間就越少,但在算法的社區標簽擴散階段則需要更多的計算,所以k的取值需要取得一個平衡,使得算法在精確度和運算時間上達到一個最佳平衡,基于此目的,本文提出節點剩余率指標(子圖節點數/節點總數),通過該指標,能夠快速的計算出各數據集的最佳k值。 表2列出了當k值取不同的特定值時,各數據集在模糊k-core子圖中的節點剩余率,直觀地顯示各數據集節點度數的分布情況,即相同k值下,節點剩余率越高,網絡的平均度數越高,節點間的聯系就越緊密。在針對不同數據集進行模糊k-core分解時,該數據集的節點剩余率是一個非常重要的參考數值,能夠迅速確定算法最佳k值的具體范圍,顯著降低最佳k值的計算時間。 圖4、圖5展示了本文所提出的基于模糊k-core的社區發現算法分別在Karate,Polbooks,Football和Dolphins這4個數據集上所得到模塊度和NMI隨著k值不同的變化趨勢。表示精確度的模塊度和NMI值在不同的數據集上隨著k值的增加都有不同程度的變化。結合表2可知,當占比率大于0.6時,模塊度值的變化相對很小,并隨著占比率的下降平緩降低。而NMI值在變化曲線上則更加復雜一些。綜合兩個精確度量值,可以得到各數據集的最優k值,見表3。 表2 各數據集在模糊k-core子圖中的節點剩余率 圖4 小數據集不同k值下的模塊度變化 圖5 小數據集不同k值下的NMI變化 表3 各數據集最優k值 根據上文所得最優k值,將本文所提出的基于模糊k-core的社區發現算法與Newman,LPA,Louvain,Walktrap,CTS和TS這6個算法在Karate,Polbooks,Football和Dolphins這4個數據集上進行算法精確度對比,對比實驗結果見表4。 通過表4中的對比可以看出,本文提出的基于模糊k-core的社區發現算法在4個數據集的對比中綜合效果最好,說明本算法在社區劃分與聚類的質量上取得了較好的結果。具體表現為,在Karate數據集的對比中,本算法與Louvain算法在NMI值上并列第一,模塊度與TS算法并列第一;Polbooks數據集的對比中,算法在NMI值上與Walktrap算法并列第一并遠高于其它算法,模塊度方面則與大部分算法持平;在Football數據集的對比中,本算法在模塊度上和大部分算法持平,但在NMI上稍落后于所對比的算法;而在Dolphins數據集的對比中,本算法在模塊度和NMI上都與效果最好的幾個算法持平。 表4 小數據集實驗對比數據 圖6、圖7展示了本文所提出的基于模糊k-core的社區發現算法分別在Amazon和Youtube這兩個數據集上所得到模塊度和所需運算時間隨著k值不同的變化趨勢。 圖6 大數據集不同k值下的模塊度變化 圖7 大數據集不同k值下的運算時間變化 在Amazon和Youtube這兩個數據集上,模塊度和運算時間隨著k值的增加都有不同程度的下降。隨著k值的增加,相對于模塊度的緩慢下降,運算時間出現大幅度下降,特別是k值從2到10的變化趨勢尤其顯著,然后k值從11到20時逐漸緩和。所以對于這兩個大規模數據集,為了追求計算效率,設置k=10的值是比較理想的方式。 為了展示本文提出的基于模糊k-core的社區發現算法在運行時間上的優越性,將與GN,LPA和Louvain這3個經典算法在SNAP所提供的Amazon和Youtube兩個大規模數據集上進行模塊度和運算時間的對比,見表5。 表5 大數據集實驗對比 通過表5的對比結果可以看出,由于GN算法和LPA算法分別是自頂向下和自底向上的全局貪心算法,且沒有明確的衡量劃分好壞的終止指標,所以其時間性能明顯較差。Louvain算法在此基礎上添加了模塊度這一標準,相比GN和LPA,明顯提高了算法的劃分精度和時間性能。但以上3個算法都針對全網的社區劃分,本文所提出的基于模糊k-core的社區發現算法則是以局部社區劃分為核心的算法,實驗數據表明,本算法在保持算法精度的同時,大幅度減少了運算時間,極大地增加了對大數據集進行社區劃分的計算效率。 本文在標準k-core分解算法的修剪規則上融合了基于模糊集理論的隸屬度概念,提出了一種以模糊k-core分解為核心的局部社區發現算法。算法提出了一種隸屬度方程,通過利用隸屬度方程對被k-core分解所刪除的節點進行二次判斷,最終確定是否將該節點保留在當前粒度層,優化了k-core分解的對節點重要性判斷的缺陷,使得更多的高重要節點得以保留在核心節點集。對模糊k-core子網進行局部社區劃分后,將劃分的社區標簽按照鄰接點集中的權重占比進行標簽擴散,最終完成全局社區發現。與其它社區發現領域的經典算法和近期提出的算法相比可知,本算法在社區發現的精確度和運行時間上都有著更好的表現。但本算法目前沒有考慮網絡中社區的重疊性,通過識別社區是否重疊,然后將重疊社區分解成為非重疊社區以進一步提高社區發現的精確度是今后研究的主要方向。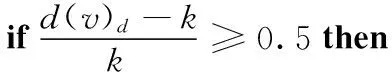
2.3 子圖社區劃分
2.4 社區標簽擴散
3 實驗分析
3.1 實驗準備
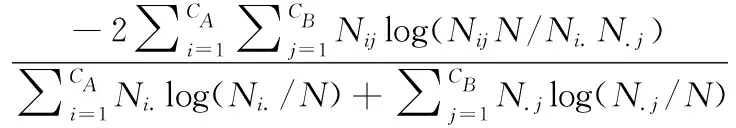
3.2 基于小數據集的算法精確性驗證
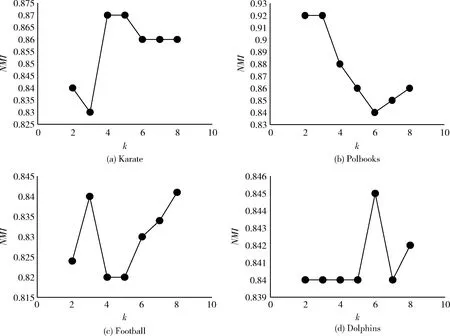
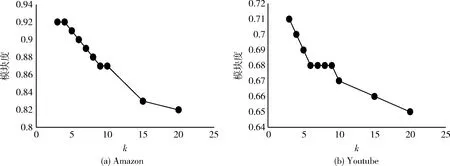
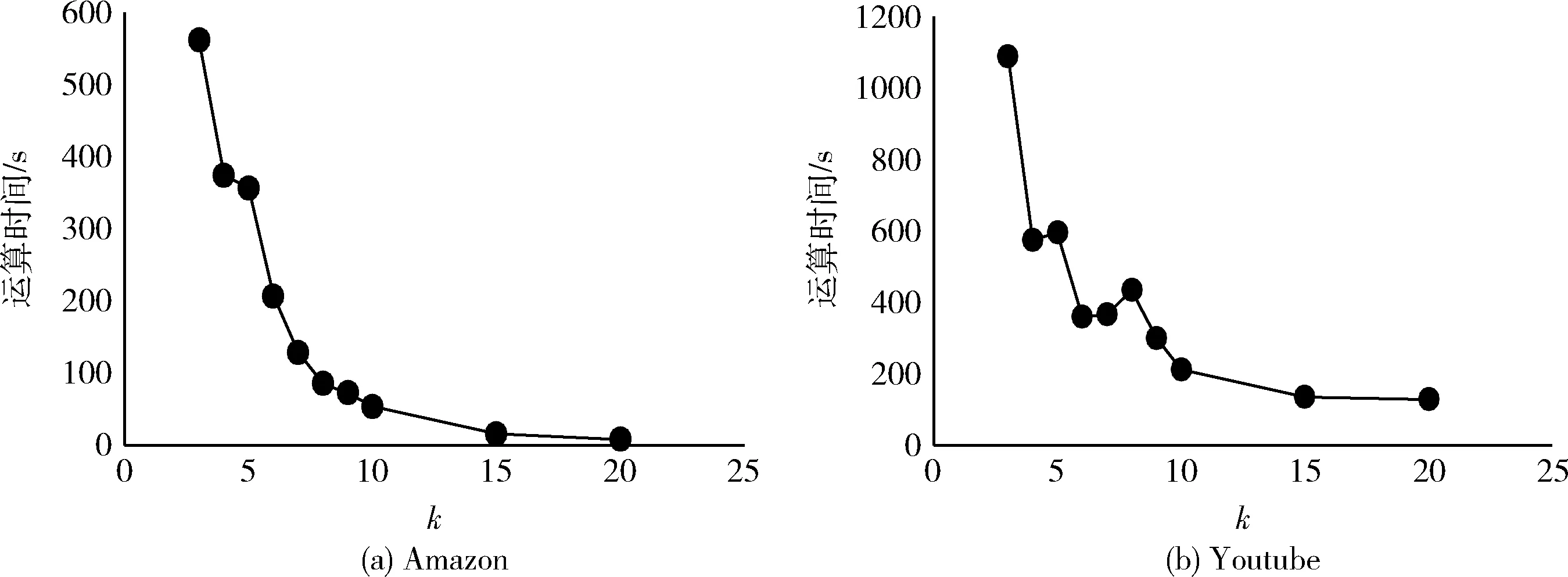
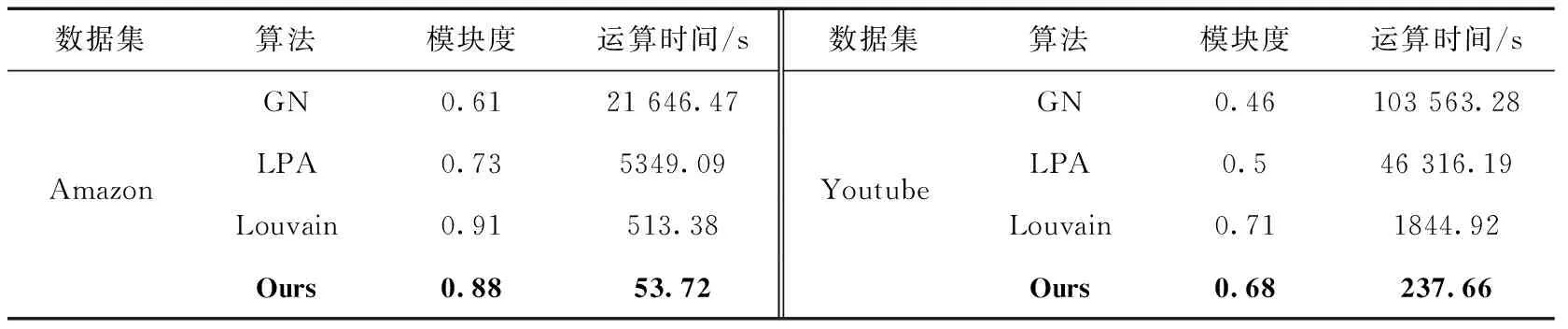
3.3 基于大數據集的算法效率驗證
4 結束語

