有色噪聲下GNSS空時抗干擾算法的性能分析和改進

趙辰乾 劉益辰 劉 欣

(中國船舶工業系統工程研究院 北京 100094)

1 引言

衛星導航系統可以在全球范圍內為用戶提供高精度的定位、導航和授時服務，在軍用和民用領域發揮著越來越大的作用。但是衛星導航信號非常脆弱，極易受到各種有意和無意信號的干擾而無法正常工作，因此衛星導航抗干擾技術一直是人們研究的熱點[1]。

衛星導航抗干擾技術主要包括時域濾波、頻域濾波、空域濾波和空時聯合濾波等，其中空時聯合濾波器[2]將陣列天線與時間延遲結構相結合，可以在不增加天線陣元個數的情況下，極大地提高抗干擾性能，因此得到了廣泛的研究與應用。空時濾波器一般采用自適應調零和波束形成兩類抗干擾算法。自適應調零算法通過在干擾方向形成零陷來抑制干擾，典型代表是功率反演算法(Power Inversion, PI)[3]。波束形成算法利用了導航衛星的方向信息，不僅在干擾方向形成零陷，還在導航衛星方向保持增益，典型代表有最小方差無失真響應(Minimum Variance Distortionless Response,MVDR)[4]、最大信干噪比(Maximum Signal Interference Noise Ratio, MSINR)[5]和最小均方誤差算法(Minimum Mean Square Error, MMSE)[6]。

目前已有大量的文獻對陣列信號模型[7,8]和抗干擾算法[9]進行了分析與研究。在理論分析中，各文獻普遍將系統噪聲視為理想白噪聲。然而在實際工程中發現許多因素都會導致非白噪聲的產生，例如抗干擾處理器模擬前端的頻率響應不理想，系統帶寬與采樣率不匹配等，且有色噪聲會降低空時抗干擾算法的性能。

當前，對這一問題進行研究的文獻較少。文獻[10]分析了采樣率和系統帶寬對空時抗干擾濾波器性能的影響，結果表明當采樣率與系統帶寬不匹配時，空時抗干擾后衛星導航信號相關曲線質量會顯著降低。而產生這一問題的根本原因就是有色噪聲。當采樣率低于系統帶寬時，噪聲信號的頻譜會產生混疊；當采樣率高于系統帶寬時，噪聲信號成為帶通形式，這兩種情況都會導致有色噪聲的產生。

本文以抗干擾后衛星導航信號的相關曲線為評價標準，從理論和實驗兩方面分析有色噪聲對空時抗干擾算法性能的影響。最后采用“對角線加載”與“子空間投影”兩種技術來改進抗干擾算法，消除有色噪聲的影響。

2 空時抗干擾理論

2.1 空時濾波器結構

空時濾波器結構模型如圖1所示。

圖1 空時濾波器結構

設空時濾波器中的天線陣元個數為M，時延階數為N。空時濾波器的處理流程為：

(1) 空時濾波器的M個天線陣元接收到M路射頻信號。

(2) 對M路射頻信號進行下變頻、濾波和采樣量化處理得到M路基帶數字信號。

(3) 對M路數字基帶信號分別進行N–1次時間延遲得到MN路信號，信號矢量可以表示為

2.2 空時抗干擾算法

空時抗干擾算法的核心是求解權向量。空時濾波器有自適應調零和波束形成兩類抗干擾算法。本文選用兩類算法的典型代表PI和MVDR來進行后續的理論分析與實驗仿真。

空時信號的協方差矩陣為

PI算法采用功率最小準則并使第1路信號全通。數學公式可以表示為

2.3 抗干擾性能評價指標

為了進一步分析有色噪聲對空時抗干擾算法性能的影響，需要首先確定抗干擾算法的性能評價指標。常用的抗干擾算法評價指標是抗干擾輸出端信號的信干噪比(Signal to Interference Plus Noise Ratio,SINR)，但是已有研究指出SINR體現的是導航信號解擴前的性能而無法正確反映信號解擴后的性能而且SINR也無法反映導航信號的失真情況[12,13]。因此本文選擇抗干擾后衛星導航信號的相關曲線作為性能評價指標。相關曲線的計算公式為[14]

3 有色噪聲的影響

本節分析有色噪聲對空時抗干擾算法性能的影響。首先假設系統噪聲具有以下兩點性質：

(1) 各通道噪聲互不相關，且與干擾信號和衛星導航信號互不相關。

(2) 各通道噪聲功率相同，且具有相同的功率譜密度函數。

空時信號的協方差矩陣可以分解為

通過上述推導可得噪聲功率譜密度函數會影響空時抗干擾后衛星導航信號的相關峰。下面通過仿真實驗驗證上述結論，同時分析噪聲功率譜的等效帶寬和譜峰偏移兩個特征對相關峰的影響。

實驗條件：空時濾波器采用4陣元平面圓陣，陣元間距為B3頻點的半波長，中頻采樣率與系統帶寬均為24 MHz。衛星導航信號采用北斗B3I信號，調制方式為BPSK，碼速率為10.23 MHz，信噪比為–20 dB，到達方向為俯仰角60°，方位角0°；干擾信號為連續波信號，干信比為100 dB，到達方向為俯仰角70°，方位角200°。

實驗1：噪聲等效帶寬對抗干擾后衛星導航信號相關峰的影響。

等效帶寬可以反映有色噪聲功率譜能量集中程度，其計算公式為

有色噪聲的等效帶寬越小，噪聲的功率譜能量越集中；等效帶寬越大，噪聲的功率譜能量越均勻；當等效帶寬為1時，噪聲功率譜為常數，噪聲信號為白噪聲，如圖2所示。

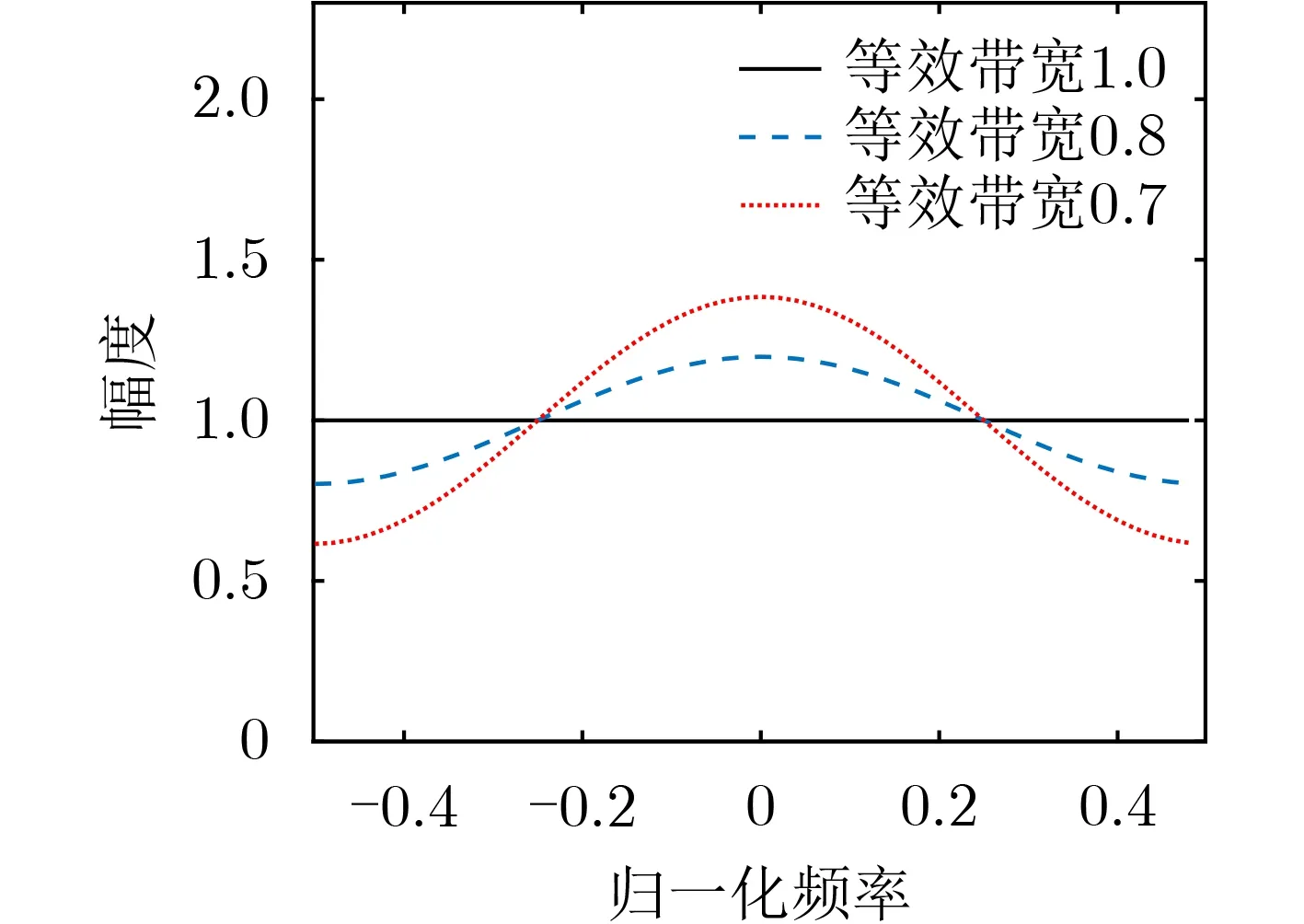
圖2 不同等效帶寬下噪聲信號的功率譜

實驗中，保持噪聲功率不變，只改變噪聲等效帶寬。噪聲信號功率譜的譜峰位于系統中心頻率且左右對稱。分別選取PI和MVDR算法進行仿真，同時改變空時濾波器的時延階數(包括1, 3, 5, 7階時延)，最后將結果與理論公式進行比較。實驗結果如圖3、圖4所示。

圖3和圖4分別采用了PI和MVDR算法，仿真了在不同時延階數的空時濾波器下，噪聲等效帶寬與抗干擾后衛星導航信號相關峰的關系。

圖3 噪聲等效帶寬與PI抗干擾后衛星導航信號相關峰的關系

圖4 噪聲等效帶寬與MVDR抗干擾后衛星導航信號相關峰的關系

通過實驗1可得到下述兩個結論：

(1) 采用1階時延結構時，即純空域濾波器，PI和MVDR算法都不會受到有色噪聲等效帶寬的影響，抗干擾后衛星導航信號的相關峰值不會衰減。

(2) 采用多階時延結構時，即空時濾波器，PI算法和MVDR算法都會受到有色噪聲等效帶寬的影響。有色噪聲等效帶寬越小，其功率譜能量越集中在中心頻點處，抗干擾后衛星導航信號的相關峰衰減越大，且隨著時延階數的增大，實驗結果趨近于理論值。

實驗2：譜峰偏移對相關峰的影響

實驗分析有色噪聲功率譜的譜峰偏移對空時抗干擾后導航信號相關峰的影響。噪聲功率譜的譜峰偏移如圖5所示。

圖5 不同譜峰偏移的噪聲信號功率譜

實驗中，保持噪聲功率和功率譜形式不變，只改變功率譜的譜峰偏移。分別選取PI和MVDR算法進行仿真，同時改變空時濾波器的時延階數(包括1, 3, 5, 7階時延)。實驗結果如圖6、圖7所示。

圖6和圖7分別采用了PI和MVDR算法，仿真了在不同時延階數的空時濾波器下，噪聲功率譜的譜峰偏移與抗干擾后衛星導航信號相關峰的關系。

圖6 噪聲譜峰偏移與PI算法抗干擾后衛星導航信號相關峰的關系

通過實驗2可得到兩個結論：

(1) 采用1階時延結構時，即純空域濾波器，PI和MVDR算法都不會受到有色噪聲譜峰偏移的影響，抗干擾后衛星導航信號的相關峰值不會衰減。

(2) 采用多階時延結構時，即空時濾波器，PI算法和MVDR算法都會受到有色噪聲譜峰偏移的影響。有色噪聲的譜峰離中心頻點越遠，衛星導航信號的相關峰值衰減越小，且隨著時延階數的增大，實驗結果趨近于理論值。

綜合實驗1和實驗2可得以下3個結論。

結論1：空域濾波器性能基本不受噪聲功率譜形式影響。

結論2：空時濾波器性能受噪聲功率譜形式影響較大，噪聲功率譜能量越集中于衛星導航功率譜譜峰處，空時濾波器處理后的衛星導航信號相關峰值越小。

結論3：時延階數越高，實驗結果越趨近于理論值，因此可以驗證理論的正確性。

4 抗干擾算法改進

通過第3節的分析可知，空時抗干擾后衛星導航信號的相關峰與噪聲功率譜形式有關。這是因為噪聲功率譜會影響噪聲協方差矩陣，然后通過矩陣求逆方式影響抗干擾算法的權向量，進而影響噪聲信號與衛星導航信號的頻率響應函數，最后影響衛星導航信號的相關峰。本節提出對角加載和子空間投影兩種方法，通過對協方差矩陣進行處理來消除有色噪聲對空時濾波器的影響。

圖8 對角加載量與相關峰衰減的關系

下面通過實驗來驗證對角加載、子空間投影算法的性能。仿真實驗的條件與第3節相同，空時濾波器的時延階數是3階，實驗中只改變抗干擾算法。

實驗結果如圖9和圖10所示，圖9為原始PI算法與經過對角加載和子空間投影后算法性能的比較，圖10為原始MVDR與經過對角加載和子空間投影后算法性能的比較。

圖9 原始PI算法和對角加載、子空間投影后算法性能的比較

圖10 原始MVDR算法和對角加載、子空間投影后算法性能的比較

通過實驗可得，采用對角加載和子空間投影算法后，空時抗干擾后衛星導航信號的相關峰基本不受噪聲等效帶寬的影響。采用子空間投影法抗干擾后，衛星導航信號的相關峰值比采用對角加載法抗干擾后的信號相關峰值高零點幾分貝，且有色噪聲等效帶寬越小，子空間投影法的性能越優于對角加載法。

對角加載法和子空間投影法都是通過對噪聲協方差矩陣的特征值進行一致化處理實現有色噪聲的白化。當噪聲信號為白噪聲時，噪聲協方差矩陣為單位矩陣，它的所有特征值均相等；當噪聲信號為有色噪聲時，噪聲協方差矩陣特征值不相等，且有色噪聲功率譜能量越集中(等效帶寬越小)，其特征值的最大最小值的差異越大，即λmax/λmin值越大。對角加載法通過引入固定的加載量k，使(λmax+k)/(λmin+k)趨近于1，從而實現有色噪聲的白化。對于固定的加載量k，有色噪聲的等效帶寬越小，(λmax+k)/(λmin+k)值會越大，噪聲白化效果降低，因此性能會下降。為解決此問題，需要增大對角加載量，但是對角加載值太大會影響算法的干擾抑制效果。子空間投影通過特征分解求得信號的干擾子空間和噪聲子空間，并將噪聲子空間中的所有特征值都置為1，因此噪聲白化更徹底且不會受到有色噪聲功率譜形式的影響，但是子空間投影法需要進行矩陣特征分解，計算復雜度更高，而且需要確定門限值來劃分噪聲子空間和干擾子空間。

5 結束語

空時濾波器對噪聲形式非常敏感，傳統的抗干擾算法如自適應調零和波束形成算法的性能都會受到有色噪聲功率譜形式的影響，有色噪聲功率譜的能量越集中于衛星導航功率譜譜峰處，抗干擾后的衛星導航信號相關峰值越小，算法性能越差。

對角加載和子空間投影方法通過對噪聲協方差矩陣特征值的一致化處理實現有色噪的白化，從而消除有色噪聲對空時抗干擾算法的影響。對角加載方法性能略低于子空間投影法且會隨著有色噪聲等效帶寬變小而下降，但計算和實現復雜度低；空間投影法性能更優且不受有色噪聲功率譜形式影響，但需要進行特征分解和門限選擇，計算和實現復雜度更高。