基于魯棒主成分分析的多域聯合雜波抑制算法

李相平 王明澤* 但 波 李 蔚 馬俊偉

①(海軍航空大學岸防兵學院 煙臺 264001)

②(海軍航空大學航空作戰勤務學院 煙臺 264001)

③(海軍航空大學航空保障專業兵訓練基地 青島 266109)

1 引言

區別于自由空間中的其他雷達，穿墻成像雷達(Through-the Wall Imaging Radar, TWIR)需要對墻后目標進行探測成像[1,2]。在這一過程中，由墻體反射造成的雜波信號會以較大的幅值來“遮蔽”目標信號，或者在時域上與目標信號交織重疊。因此，有效抑制墻體雜波[3]，是TWIR對墻后目標準確成像的重要前提。

諸如奇異值分解[4](Singular Value Decomposition, SVD)一類的經典雜波抑制算法，僅能實現對主墻體雜波的消除，而殘余雜波會顯著降低目標成像質量。隨著對TWIR的廣泛應用和深入研究，目標檢測、識別等工作對前期成像的要求越發嚴格，現有的雜波抑制算法難以達到穿墻成像的實時性和準確性條件。

近年來，機器學習理論被逐漸引入TWIR領域，如壓縮感知[5,6](Compressive Sensing, CS)、矩陣補全[7](Matrix Completion, MC)以及魯棒主成分分析[8](Robust Principal Component Analysis, RPCA)。其中，作為高光譜圖像去噪及視頻監控中的前景提取等研究方向的常用工具，RPCA[9]可以將數據矩陣唯一分解為低秩雜波矩陣與稀疏目標矩陣，即同時實現對雜波與目標的準確分離。對應于數據矩陣為穿墻回波矩陣或穿墻圖像矩陣，RPCA可以分離得到其中的目標回波信號或目標像素分量，進而實現雜波抑制。所以，在本文中，基于RPCA理論，提出一種新的雜波抑制算法。

為滿足穿墻成像的實時性和準確性要求，分別就算法的速度和精度進行設計改進：一是提出光滑化快速交替線性化方法來縮短RPCA問題的求解時間，從而加快算法的速度；二是多域聯合處理，同時在回波域和圖像域應用RPCA理論，通過對其得到的目標圖像進行指數加權聯乘融合處理來提高算法精度。

綜上所述，本文的章節安排如下：第2節介紹RPCA原理；對回波域和圖像域建模的工作在第3節完成；第4節對所提雜波抑制算法進行理論分析；在第5節設計穿墻場景仿真，通過與多種算法的性能對比，驗證所提算法的速度和精度；最后在第6節總結全文。

2 RPCA原理

其中，//A//?表示矩陣A的核范數，//E//1表示矩陣E的l1范數。在這里，矩陣A和E要達到秩稀疏不相干的條件，以確保凸優化問題的正確求解。顯然，在相當廣泛的情況下，該條件都是成立的，即矩陣A和E可以被高概率地精確恢復[13]。

對于式(3)中RPCA問題的求解，有以下幾種常用的1階方法：一是加速近端梯度[14](Accelerated Proximal Gradient, APG)方法，以線性化函數來實現對目標函數的局部逼近，使得單次迭代的計算量較小，但收斂速度較慢；二是精確增廣拉格朗日乘子[15](Exact Augmented Lagrange Multipliers,EALM)方法，通過交替迭代增廣拉格朗日函數來得到矩陣A和E，可實現高階線性收斂，不過每次迭代的SVD次數較多，大大影響了計算速度；三是非精確增廣拉格朗日乘子[15](Inexact Augmented Lagrange Multipliers, IALM)方法，將EALM中的多輪交替最小化削減為1輪，可在保持原有收斂速度的基礎上有效減少SVD次數。

3 聯合低秩稀疏模型

3.1 回波域建模

首先，設定成像場景如下：TWIR以收發同置的均勻天線陣列對墻后目標進行探測成像，陣元數量為N，且天線陣列與勻質墻體表面平行，則第n個天線陣元所接收的回波信號為

其中，uw(n,t)為墻體雜波信號，utg(n,t)為目標回波信號，uno(n,t)為噪聲信號，uant(n,t)為天線耦合信號。在本文中，認為天線耦合波經預處理后被消除；且為便于建模分析，假設噪聲信號對目標成像的影響相對有限，則回波信號可進一步簡化為

隨后，將式(5)的結果擴展至整個天線陣列，有2維回波矩陣

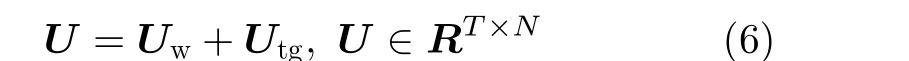
其中，T為各天線通道信號的采樣點數，Uw為雜波信號矩陣，Utg為目標信號矩陣。

在上述成像場景下，單就墻體雜波信號來講，各天線陣元對應的墻體反射系數及信號傳輸路徑是相同的，則其各自接收的墻體反射回波也是相同的[16–18]，即Uw是低秩矩陣。從空間上看，墻后目標相對于整個探測區域是稀疏的；類似地，在回波域中，目標采樣點相對于所有采樣點也是稀疏的，即Utg為稀疏矩陣。那么，根據式(3)，在回波域中建立聯合低秩稀疏[19](Joint Low-Rank and Sparse,JLRS)模型，有

3.2 圖像域建模

相較于回波域，圖像域是對探測區域的直觀表現，其應用RPCA理論的效果理應更好[20]。對于式(6)中的2維回波矩陣，以后向投影 (Back Projection, BP)算法進行成像處理，則圖像中任一像素的幅度為

4 理論分析

4.1 光滑化快速交替線性化方法

根據上文對RPCA問題求解方法的分析，可以得到：線性化近似會減小單次迭代的計算量，而交替迭代會加速收斂，降低迭代復雜度。由此出發，為了加快RPCA問題求解速度，在這里提出一種光滑化快速交替線性化(Smoothing Fast Alternating Linearization, SFAL)方法。

4.2 指數加權聯乘多域圖像融合處理

根據之前所建立的JLRS模型，不難發現，雜波和目標在各域中并非總是保持嚴格低秩或嚴格稀疏的。在回波域中，雜波的低秩性較好，目標的稀疏性較弱，在圖像域中則恰恰相反。二者在性質上呈現出一種“互補關系”，而這種關系在各域得到的目標圖像中體現得尤為明顯。為了提高算法精度、改善目標成像質量，對目標圖像進行指數加權聯乘多域圖像融合處理。

首先，對回波域和圖像域中的目標圖像作如下分析：在回波域中，JLRS模型中的目標信號矩陣為實矩陣(對原始回波數據取模求得)，隱藏了目標的相位信息，由此得到的目標圖像相當于非相干BP成像結果，再加上殘余雜波的影響，其方位向分辨率和聚焦效果都有所降低，但墻體主雜波抑制相對徹底；在圖像域中，對原始回波成像直接進行分解，此時的目標圖像為相干BP成像結果，其目標聚焦效果相對較好，但雜波分離不夠徹底，且對目標形成一定的“遮蔽”效應。

經上述分析可得，相較于多通道或多角度的子圖像融合，回波域和圖像域中的目標圖像存在一定的差異性，基本的聯乘融合[26]對目標成像質量的改善很是有限。由此提出如下的指數加權聯乘融合思路，即

隨著加權指數a的增大，回波域目標圖像在融合圖像中的貢獻相應增加，雜波被逐漸消除；在雜波基本消失后，繼續增大加權指數，便會造成目標像素的損失，因此找到雜波消失的節點顯得尤為重要。然而，在這一過程中，像素均值持續下降，且下降速度并沒有出現明顯的變化點。

表1 SFAL方法

不過，受此啟發，可考慮超均值像素數這一指標。相較于像素均值，超均值像素數能更加全面地描述圖像中像素變化的整體情況和局部細節，尤其是雜波像素和目標像素的幅度變化過程。設圖像中所有像素點的集合為S，則該指標的定義為

其中，幅度超過像素均值的像素點的集合B ?S,crad(B)表示集合B的元素個數。

同樣是在加權指數增大的過程中，超均值像素數呈現出有規律的變化：從一開始，隨著幅度較大的雜波像素被消除，超均值像素數以較快的速度持續減少；在雜波基本消失后，目標像素成為圖像中待消除像素的“主體”，指標的減少速度會明顯放緩。所以，以超均值像素數作為評價指標，并以其減速放緩的第一個點作為加權指數a。

4.3 算法思路整合

結合上文內容，對所提雜波抑制算法的思路作進一步整合，其整體流程如圖1所示。

圖1 雜波抑制算法流程圖

同時，對算法的主要步驟可歸納如下：

第1階段：利用SFAL方法得到各域中的目標圖像，包括步驟1和步驟2。

步驟1 根據穿墻雷達回波信號，直接建立回波域JLRS模型；同時，以BP算法處理回波信號，得到原始圖像，并以此建立圖像域JLRS模型；

步驟2 利用SFAL方法依次求解各域中的JLRS模型，分別得到各域中的目標圖像；

第2階段：對各域中的目標圖像進行指數加權聯乘融合處理，包括步驟3和步驟4。

步驟3 給定b=1，并在a ∈[0,1]的范圍內以0.05的步長繪制超均值像素數的變化曲線，以曲線減速明顯放緩的第一個點作為加權指數a；

步驟4 根據選定的加權指數a和b進行指數加權聯乘多域圖像融合處理，得到最終的融合圖像。

5 仿真驗證

為了驗證本文所提雜波抑制算法的速度與精度，利用MATLAB構建如下的穿墻場景：選擇勻質混凝土墻體，其厚度為0.2m，相對介電常數為5.0，磁導率為4π×10?7H/m，電導率為5.0×10?2S/m。天線陣列為均勻線陣，陣列孔徑為2 m，陣元間距為0.1 m，陣元數量N=21，其距離墻體的垂直距離為1.0 m。天線工作在收發同置模式，各陣元依次發射信號并由自身接收回波，且各天線通道信號的采樣點數T=1024。發射信號為單位幅度的高斯脈沖2階導信號，脈沖形成因子為0.5 ns，脈沖持續時間約為1.1 ns，對應的–3 dB頻譜范圍為0.8～2.6 GHz。探測區域為墻后2×2.8 m的范圍，共放置4個半徑為3.5 cm的金屬小球，各金屬球完全相同，在此場景的分辨率下可視作點目標處理。場景如圖2所示。

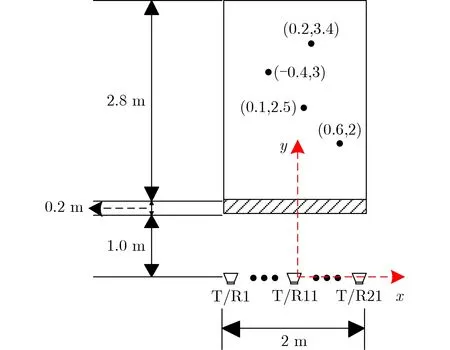
圖2 穿墻場景示意圖

5.1 算法速度

在本文中，對算法速度的改進主要體現在對RPCA問題求解方法的優化。那么，不妨以圖像域JLRS模型為例，驗證SFAL方法的性能。

首先，在上述穿墻場景下進行目標探測，以BP算法對回波信號處理成像，成像網格設置為256×256，并建立JLRS模型。隨后，依次以SFAL,APG, EALM, IALM方法求解該模型，得到目標圖像。在參數設置方面，各方法采用默認參數，其迭代終止閾值統一設定為ζ=10?7。在運行環境方面，所用聯想臺式機配置Intel Core i7-9700 3.00 GHz的8核中央處理器，其安裝內存為8 GB，仿真軟件為Windows 7系統下的MATLAB R2018b軟件。最后，以迭代時間和目標雜波比等指標對各方法的速度及準確度進行對比，具體情況如表2所示。為了不失一般性，表中各數據均為多次獨立重復試驗結果的平均值。

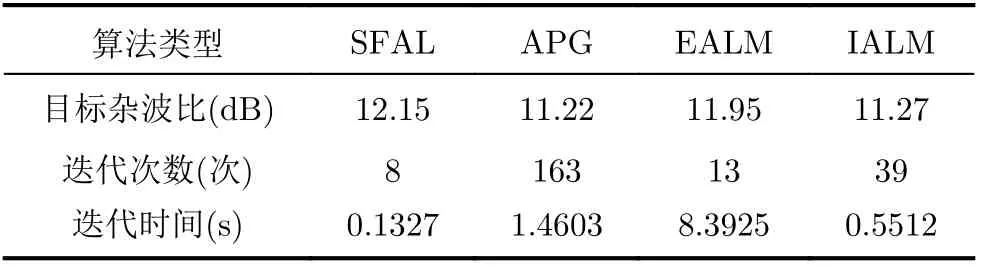
表2 各方法性能對比

在準確度方面，各方法所得目標圖像的目標雜波比基本持平，說明其目標成像質量相近；在速度方面，SFAL方法的迭代次數最少，迭代時間最短，相較于迭代次數較少的EALM方法及迭代時間較短的IALM方法仍有較大優勢。總的來看，在準確度相當的前提下，SFAL方法以其速度優勢展現出了良好的性能，而這也進一步加快了雜波抑制算法的整體速度。

5.2 算法精度

為了驗證算法的精度，同樣以圖2的穿墻場景進行探測成像，其結果如圖3所示。可以看到，其中只有墻體位置附近成像清晰，隱約可見墻后目標陰影。以本文所提算法進行雜波抑制，建立求解回波域和圖像域JLRS模型，得到各自的目標圖像，其結果分別如圖4、圖5所示。前者的墻體主雜波抑制較為徹底，但目標散焦嚴重，難以準確定位，且部分目標丟失；后者的目標聚焦準確，但不夠清晰，且墻體位置附近有殘余雜波。顯然，單一域中的目標圖像均未達到對目標成像質量的要求。

圖3 原始回波成像

圖4 回波域目標圖像

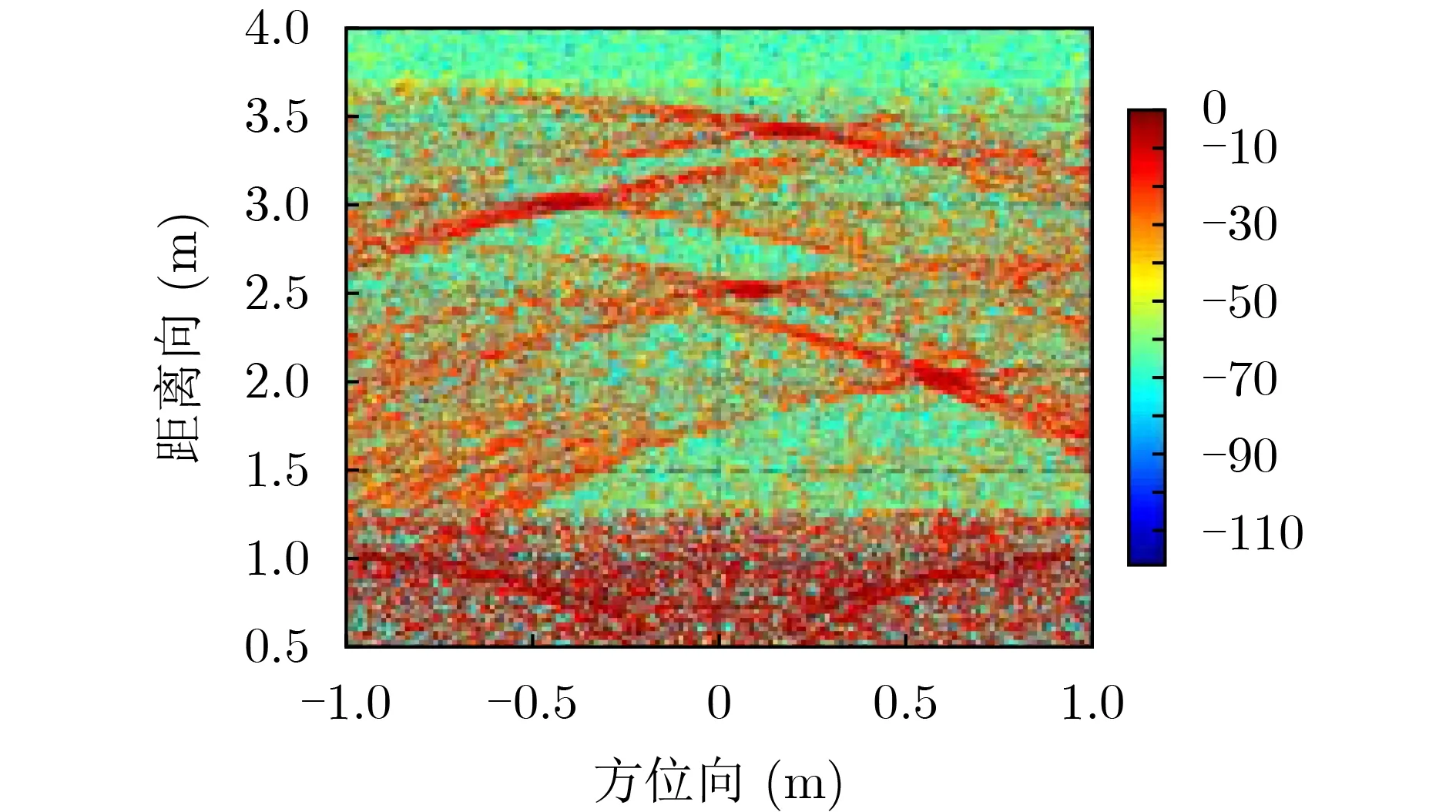
圖5 圖像域目標圖像

在進行多域聯合處理之前，對加權指數a繪制超均值像素數的變化曲線。由圖6可知，整體上該曲線呈下降趨勢，初期的上升峰值可解釋為雜波像素的快速消除和像素均值的急速下降所導致的超均值像素數的短暫增加，另有回波域加權指數a=0.65。同時，給定圖像域加權指數b=1。

圖6 超均值像素數變化曲線

根據上面得到的加權指數，進行指數加權聯乘多域圖像融合處理，最終成像結果如圖7所示。相較于圖8的背景對消成像和圖9的SVD算法成像，多域聯合成像中對墻體雜波尤其是殘余雜波的抑制更為徹底，目標成像較為清晰，聚焦效果更好。

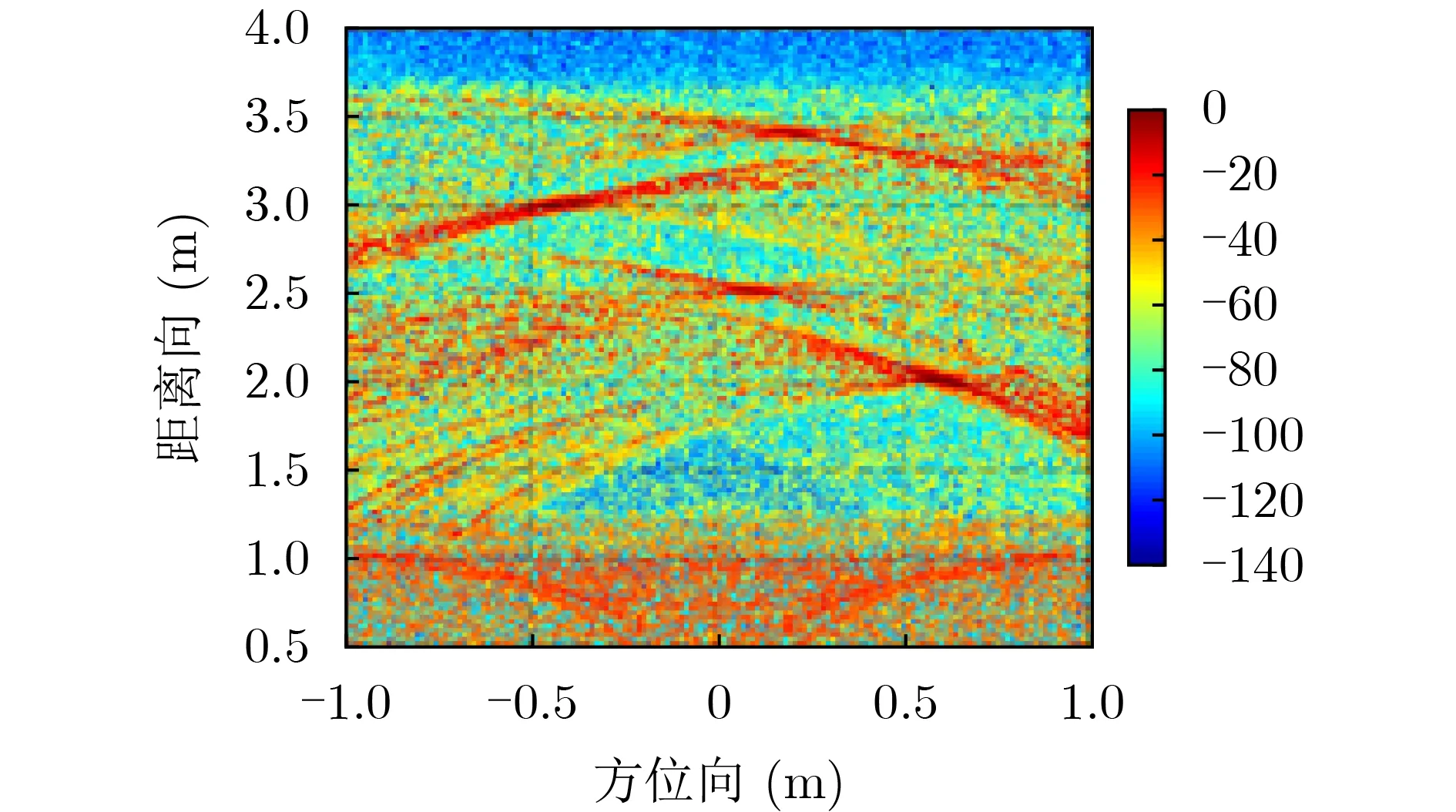
圖7 多域聯合成像

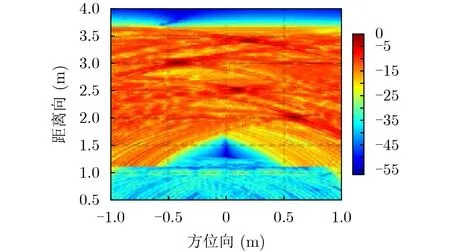
圖9 SVD算法成像

此外，以目標雜波比來定量分析算法的精度，相應數據如表3所示。可以看到，與SVD算法和背景對消相比，本文所提算法對原始成像中目標雜波比的提升異常明顯。總的來看，本文所提算法精度較高，能夠較為徹底地抑制雜波，有效提升目標雜波比。

表3 各情況下的目標雜波比(dB)

6 結束語

本文針對穿墻雷達雜波抑制問題提出一種基于RPCA理論的多域聯合抑制算法，該算法通過多域圖像融合使目標成像準確聚焦，并利用SFAL方法來增強這一過程的實時性。經仿真證明，該算法具有良好的速度和精度，可實現對雜波的充分抑制，能夠快速地為目標檢測、識別等后續處理提供準確的目標信息。

實際上，本文算法仍限于BP成像和收發同置的工作模式。為了更廣泛地適用于穿墻雷達領域，可考慮將所提算法推廣至更一般的穿墻場景，如工作在收發分置模式下的天線陣列。而這意味著要解決一個關鍵問題，即雜波低秩性和目標稀疏性的增強問題。JLRS模型越標準，雜波和目標的分離就越徹底，目標成像質量就越高。同時，從降低單次迭代復雜度的角度入手來優化RPCA求解方法，可使算法的運算速度邁向新的臺階。