基于差分濾波的非線性估計及校正方法

趙 博 張曰義 徐源鴻 劉小軍 方廣有

(中國科學院空天信息創新研究院 北京 100094 )

(中國科學院電磁輻射與探測技術重點實驗室 北京 100190)

(中國科學院大學電子電氣與通信工程學院 北京 100049)

1 引言

與傳統的脈沖體制的雷達相比，調頻連續波(Frequency Modulated Continues Waveform,FMCW)雷達具有低成本、更高的距離分辨率、更強的穿透能力、能夠消除距離盲區等優勢，因此，調頻連續波雷達在高精度測距和成像領域得到廣泛應用[1–3]，例如小型無人機遙感偵察以及淺層地質結構的精細探測[4,5]。

影響調頻連續波雷達測距成像精度最關鍵的因素是線性調頻信號的線性度[6]，調頻連續波信號具有大帶寬，且信號持續整個發射周期，因此保持信號調頻斜率的線性具有很大的難度。由于雷達系統各個器件的非理想特性，或多或少地會引入信號調頻的畸變—調頻非線性[7]。線性調頻信號中的這種非線性分量，經過去調頻處理(dechirp)之后，會引入空變的相位誤差，降低信號質量，這會對信號頻譜產生一定的影響，例如主瓣展寬、主瓣偏移、非對稱畸變、成對回波以及旁瓣能量過高等問題[8]，嚴重影響測距精度以及成像質量。

非線性模型可以分為非周期性非線性模型和周期性非線性模型，目前大多研究成果主要是針對非周期性模型即多項式模型進行估計和校正。文獻[9]提出利用高階模糊函數(High-order Ambiguity Function, HAF)估計多項式系數，通過時域插值重采樣對空變非線性進行校正，但是參數遞進估計過程會導致誤差逐漸變大的問題。文獻[10]利用遞推最小二乘法估計非線性多項式模型，利用多項式回歸實現系數的聯合估計，但是算法過程中需要對矩陣求逆，計算量以及復雜度比較大。文獻[11]使用小波變換方法提高了信號的時頻分辨率，再利用脊線檢測(ridge detection)獲得信號頻率，從而估計多項式系數。不基于多項式模型的估計方法也已經有不少學者研究。文獻[12]利用拉格朗日中值定理，從而將差頻非線性近似為1階導數與時延的乘積形式，通過相干積分即可獲得射頻非線性的估計，但是對參考時延要求比較高，且該估計是有偏的。文獻[13]利用同態濾波方法獲得射頻非線性的估計，再通過基于RVP項校正的方法，對差頻信號中的非線性進行校正，但是噪聲魯棒性較低且存在相位模糊，而文獻[8]在此基礎上提出了根同態方法對射頻非線性進行估計，改進了同態濾波方法，然而同態域實現條件在實際中較為苛刻。

本文針對上述問題展開深入研究，提出了一種新的FMCW雷達非線性估計以及校正方法。首先，建立了調頻連續波差頻信號在非線性干擾情況下的模型，分析了非線性對雷達距離成像造成的影響；然后，利用差頻信號非線性模型的特點建立差分方程，估計目標時延對應的離散時延，再利用z變換域法解差分方程，從而獲得射頻非線性的估計；最后，通過匹配傅里葉變換校正差頻非線性，從而消除非線性影響，提高測距精度以及成像質量。仿真結果充分證明了算法的有效性，并通過實際探測數據進行了驗證。

2 非線性信號模型

為了減少ADC的采樣頻率，將接收信號與發射信號做混頻即Dechirp處理之后[16]，可以得到差頻信號。因此存在非線性誤差的差頻信號可以表示為

3 算法原理

3.1 差分濾波射頻非線性估計

另外，由于Nτ與τ的不匹配問題，估計出的ε[n]可能會存在“毛刺”，需要濾除掉這些“毛刺”，否則會引入新的正弦非線性量。

3.2 匹配傅里葉變換校正非線性

匹配傅里葉變換(Match Fourier Transform,MFT)算法是一種針對非線性調制信號提出的廣義傅里葉變換，該方法根據信號形式調整變換基，可以同時實現多目標在匹配傅里葉域的分辨[18]。

當目標距離不是特別遠，即目標時延不是特別大時，可以獲得近似表示：ε(t)?ε(t ?τ)≈τε′(t)，則多目標情況下的差頻信號可以表示為

綜上，本文提出的基于差分方程濾波的非線性估計校正方法流程如圖1所示。

圖1 基于差分濾波的非線性估計校正方法流程

4 仿真實驗及比較分析

對本文提出的非線性相位估計校正算法進行仿真分析，從而驗證所提出算法的有效性。使用單點目標回波根據算法原理估計射頻非線性相位，非線性相位模型如式(2)所示，為簡便計算，多項式模型僅使用3次和4次項，正弦誤差使用低頻以及高頻兩項。雷達系統參數如表1所示。

表1 雷達系統仿真參數

為了定性分析非線性對信號的影響以及算法的估計校正效果，引入非線性度的概念。線性調頻連續波信號的非線性可以表示為式(12)所示，非線性度即為max[ρ(t)]。為了突出顯示非線性的影響，在本仿真中的非線性度為1.20 %，其射頻信號的非線性ε(t)如圖2所示。

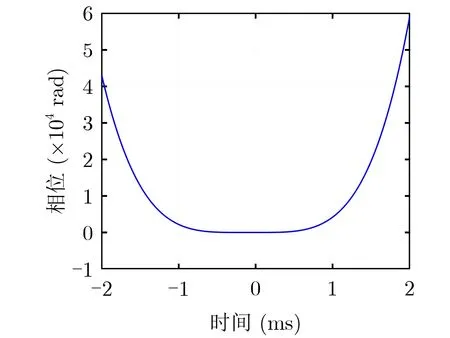
圖2 射頻信號的非線性ε(t)

在進行非線性的估計中由于僅涉及相位信息，為了確保該估計方法能夠在實際當中的正常應用，在該仿真中對差頻信號的相位加入信噪比為20 dB的白噪聲。在此非線性的干擾下，該調頻連續波的差頻信號的時域波形與歸一化頻譜如圖3所示。該仿真中，目標時延對應的差頻頻率為fb=Kτ=750kHz，而該信號的頻譜中獲得的差頻頻率為750.6kHz，頻譜發生偏移，產生了嚴重的非對稱性畸變，且在主瓣兩邊產生了成對回波，測距精度以及成像質量惡化情況非常嚴重。

圖3 差頻信號時域波形與歸一化頻譜圖

提取該差頻信號的相位并解纏繞，其相位與頻率(相位對時間的導數)如圖4所示，從圖中可以看出，相位與時間呈1次線性關系，但是受到了非線性以及噪聲的干擾。

圖4 差頻信號相位與時頻曲線

構造理想差頻信號并與該差頻信號混頻，即可得到差頻非線性項???(t)，其離散形式如式(6)所示。τ與Nτ的偏差會影響估計的準確性，因此需要對差頻信號升采樣，以減小τ與Nτ的偏差，設定偏差為0.1，進行升采樣處理。由式(8)即可獲得該信號的非線性估計，如圖5所示，差分濾波方法可以估計出非線性相位ε[n]，但是會產生“毛刺”，需要對該估計結果平滑處理，消除“毛刺”，使用平滑窗對“毛刺”進行平滑處理，平滑窗長度不應太大，避免將頻率較高的周期性非線性相位濾除掉，平滑窗的長度應設置在2～5個“毛刺”周期長度。對“毛刺”的平滑結果如圖5所示。

圖5 非線性估計結果；“毛刺”現象與平滑處理結果

由于進行了升采樣的處理，該估計的非線性數據長度與原數據不一致，因此還要進行降采樣處理，使其數據長度保持一致。

差分濾波方法、相干積分法與實際非線性的比較如圖6(a)所示，從圖中可以看出，差分濾波方法與相干積分法的估計結果基本一致。

相干積分方法與本文提出方法的估計誤差對比如圖6(b)所示，從圖中可以看出，本文提出的估計方法的估計誤差遠小于相干積分方法的估計誤差，因此本文提出的估計方法更加準確。用本文提出的方法估計出的非線性項進行校正，校正結果如圖7所示。從圖中可以看出，使用MFT校正后，因為非線性造成的頻譜偏移得到一定的校正，且非對稱性的畸變也得到了校正。而在非線性度為1.20%的情況下，使用基于RVP項校正的方法效果變得很差。

圖6 兩種方法的相位與相位差對比

圖7 RVP和MFT校正結果對比

5 實測數據驗證

使用本實驗室提供的FMCW雷達進行實測數據的驗證，該雷達主要的系統設計參數如表2所示。

表2 雷達系統設計參數

首先，進行閉環測試以估計該雷達射頻非線性相位。閉環測試數據的歸一化頻譜如圖8所示，從圖中可以看出，該信號受到了非線性的影響，主瓣附近產生了非對稱畸變，而且在主瓣附近也有一些對稱回波干擾導致旁瓣能量升高，且右側旁瓣能量比左側旁瓣能量高出許多。

圖8 閉環差頻數據歸一化頻譜

按照本文提出的非線性估計方法，估計出的射頻非線性相位如圖9(a)所示，其中的周期性非線性相位如圖9(b)所示。由于該信號末端為非調頻段，因此會造成相位的偏差以及非線性度的增加，在進行數據處理時需截掉末端非調頻段。經計算，該系統非線性度約為0.631%。

圖9 射頻非線性相位以及其中的周期性非線性相位估計結果

使用上述估計非線性相位，利用匹配傅里葉變換校正方法對另一條延遲線閉環數據進行非線性校正，校正前后的差頻頻譜如圖10所示，從圖中可以看出，經過匹配傅里葉變換校正之后，因非線性造成的主瓣展寬、旁瓣能量過大、非對稱畸變、對稱回波等都有所抑制。

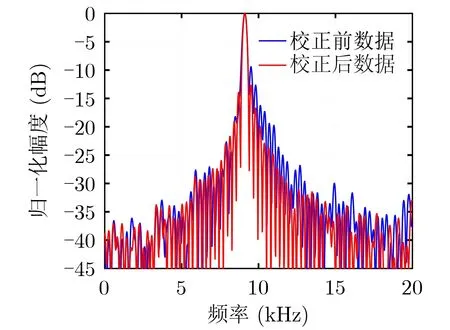
圖10 閉環數據非線性校正結果對比

使用上述閉環測試估計出的射頻非線性相位，對該雷達在野外探地試驗數據進行非線性校正，其校正前的圖像如圖11所示，可以看到在移動方向20～30 m、深度0.8～2 m的范圍內有一個分層目標。在經過非線性校正之后的圖像如圖12所示。從閉環數據的校正結果來看，非線性校正的效果主要體現在抑制旁瓣能量方面，為了定量地分析非線性校正算法的改善效果，計算圖11與圖12中黑色方框內的峰值旁瓣比的總和plsrsum，由于非線性校正只針對目標響應有效，在計算plsrsum時，僅計算紅色方框標出的位置。圖11中計算出的峰值旁瓣比總和為plsrsum1=?120.035 dB，圖12中計算出的峰值旁瓣比總和為plsrsum2=?196.682 dB，則改善效果為

圖11 實測數據成像

圖12 校正之后的實際圖像

選取其中一道數據進行分析，其校正前后對比圖像如圖13所示。圖中低于0.2 dB的信號可認為是無效信號，即噪聲強度比較高，該部分非線性校正效果不在考慮范圍內。在該實際的野外探測數據中，由于探測到的目標是具有一定的厚度的地質分層，因此分層的厚度以及較高的噪聲強度均會造成旁瓣的升高。從圖中可以看出，主瓣右側較高能量的旁瓣得到了有效抑制，主瓣兩側能量基本對稱分布，非線性得到有效抑制，增強了雷達對回波動態范圍較大的相鄰目標的檢測能力。

圖13 目標處其中一道數據校正前后效果對比

6 結束語

本文針對線性調頻連續波信號以及非線性特征建立了受到非線性影響的線性調頻連續波信號模型。首先針對差頻信號中非線性項的特征即差分形式提出了差分濾波的方法對射頻非線性進行估計，能夠同時對周期性以及非周期性非線性進行估計，通過仿真實驗表明，該估計方法相比于相干積分估計方法的估計精度更高，且在噪聲影響下也具有較高的估計精度。然后使用匹配傅里葉變換校正方法對信號進行非線性校正，通過仿真實驗表明，該校正方法在非線性度較大的情況下比基于RVP的校正方法更加有效。最后通過線性調頻連續波雷達的實測數據驗證了該非線性估計及校正方法的有效性。