U型不完全多目標拆卸線平衡問題建模與優化
張則強 ,蔣 晉 ,尹 濤 ,許培玉
(1. 西南交通大學機械工程學院,四川 成都 610031;2. 西南交通大學軌道交通運維技術與裝備四川省重點實驗室,四川 成都 610031)
拆卸線是實現廢舊機電產品規模化和自動化生產的重要組織方式,而如何提高拆卸效率和生產線平衡率,引起學者們的廣泛關注,由此提出拆卸線平衡問題(disassembly line balancing problem,DLBP)[1].
關于DLBP問題的研究多集中于直線型DLBP問題優化[1-4]. 在實際的生產作業中,相較于直線型布局方式,最大的不同之處在于U型拆卸線在設計過程中可從前后雙向搜索可分配作業任務,并可將首尾兩個作業任務分配到同一個工作站. 此外,U型布局具有生產柔性強、占地面積小、效率高等特點[5].肖欽心等[6]考慮U型布局下拆卸過程存在的多種約束限制,以最小化拆卸節拍時間和工作站空閑時間指標為優化目標,采用改進的并行鄰域搜索算法進行求解. 張則強等[7]提出一種Pareto蟻群遺傳算法,對多目標U型拆卸線平衡問題進行協同優化,以彌補傳統求解方法的不足. 拆卸作業過程中,由于部分零件存在需求性或危害性,需要后續相關處理操作,因此必須拆卸,其余零部件則可選擇性進行拆卸,由此能節約成本,提高拆卸效率. Ren等[3]建立了以利潤為導向的不完全拆卸線問題模型,并通過引力搜索算法求解. Bentaha等[4]利用AND/OR優先關系圖,通過基于拉格朗日松弛和蒙特卡洛采樣技術的求解方法,解決以利潤為最高要求的不完全拆卸線平衡問題. 因此,本文綜合考慮U型布局的柔性生產特點和不完全拆卸的高效性,提出U型不完全拆卸線平衡問題(U-shaped partial disassembly line balance problem,UPDLBP).
對于DLBP問題的求解方法研究,Güng?r等[8]首次證明DLBP是NP-hard問題,其解空間隨著問題規模的增長呈指數增長,因此,數學規劃方法[9-10]不適用于求解大規模DLBP. 而啟發式算法[11-12]依賴啟發式規則,采用先決策后優化的形式,將多目標轉化為單目標進行計算,只能獲得一個容易受決策者主觀因素影響的解. 目前,群智能算法例如人工蜂群算法[13]、變鄰域搜索算法[14]、蟻群算法[15]等由于全局尋優能力強和適用范圍廣等特點,在DLBP中得到廣泛應用.
與其他算法相比,狼群算法(wolfpack algorithm,WPA)[16]受參數設置影響性較低,在求解速度和求解質量上更具優勢. 本文提出一種自適應反向學習多目標狼群算法(adaptive opposition-based learning multiobjective wolfpack algorithm,AOBL-MWPA),通過對算法進行離散化操作,利用輪盤賭操作劃分狼群;采用自適應游走行為,在迭代前期增強全局尋優能力,后期增強局部搜索能力,加強探狼間信息交互,其余人工狼通過奔襲行為和召喚行為向當前迭代次數的全局最優解靠攏;引入反向學習策略(oppositionbased learning,OBL)[17]避免算法陷入局部最優解;通過精英保留策略記錄全局最優解,最后引入Pareto解集思想[18]和非支配排序遺傳算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)擁擠距離機制[19]獲得分布均勻的非劣解集.
1 U型不完全DLBP問題
1.1 問題描述
本文從實際角度出發,考慮采用U型布局和不完全拆卸方式,如圖1所示,工人同時對U型入口側和出口側零部件進行拆卸,非必須拆卸的零部件直接進行粉碎處理,降低拆卸成本,提高拆卸效率.對UPDLBP展開研究,并作出以下假定:1) 待拆卸產品單一,且能保證長期供應不中斷;2) 零部件完整,且拆卸作業時間為標準定值;3) 忽略任何突發情況;4) 為簡化問題,不考慮工人行走、物料運輸等其他因素影響.

圖1 U型不完全拆卸線Fig. 1 U-shaped partial disassembly line
1.2 符號說明
i,j:任務編號,i,j= 1,2,···,N;
k:工作站編號,k= 1,2,···,K;
TC:拆卸節拍時間;
Tk:第k個工作站的實際工作時間;
ti:任務i作業時間;
hi:若任務i具有危害性,hi=1 ,否則hi=0;
di:若任務i具有需求性,di=1 ,否則di=0;
wk:若工作站k的拆卸任務集中存在危害性零部件,wk=1 ,否則wk=0;
Pij:若任務i為任務j的緊前任務,Pij=1,否則Pij=0. 優先關系矩陣P= (Pij)N×N;
Ci:任務i單位時間作業成本;
Ch:工作站單位時間附加無害化處理成本;
Cs:工作站單位時間待機成本;
xik:決策變量,若任務i分配到工作站k的入口側,xik=1,否則xik= 0 ;
yik:決策變量,若任務i分配到工作站k的出口側,yik=1,否則yik= 0;
Sk:決策變量,若開啟工作站k,Sk=1,否則Sk=0 .
1.3 優化目標
實際DLBP問題中,決策者希望同時優化多個目標,既能保證企業的經濟效益,降低企業成本,還能保證拆卸線的平衡性. 因此,本文考慮協同優化以下4個目標:最小化工作站數量f1、最小化空閑時間均衡指標f2、最小化拆卸深度f3及最小化拆卸成本f4,分別如式(1) ~ (4)所示,其中,拆卸成本由拆卸作業成本、工作站待機空閑成本及附加無害化處理成本三部分組成.

1.4 約束條件
約束條件包括節拍時間約束,任務分配約束,優先關系約束,需求、危害指標約束和工作約束.
節拍時間約束為

由于采用不完全拆卸方式,允許存在部分零部件不拆卸,但拆卸任務有且僅能分配到一個工作站.任務分配約束如式(6)所示.
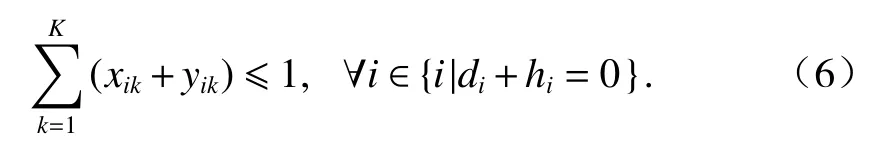
采用U型布局形式,待拆卸零部件可在入口側或出口側進行拆卸,分別加以優先關系約束. 優先關系約束如式(7)所示.

具有危害屬性和經濟效益的零部件必須拆卸.需求、危害指標約束如式(8)所示.
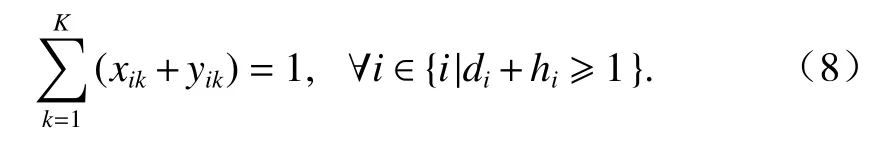
需要開啟的工作站存在理論上下閾值約束,且不允許開啟空的工作站內無任務分配. 工位約束如式(9)、(10)所示.
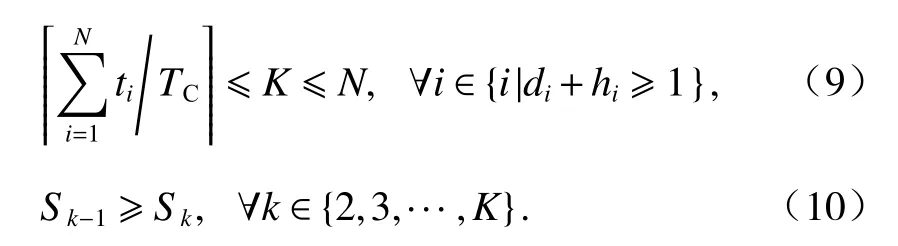
2 AOBL-MWPA算法設計
本文結合DLBP實際問題特點,提出一種自適應反向學習多目標狼群算法進行求解計算,由于DLBP問題中需要優化多個存在一定制衡性的目標,很難同時達到最優值,因此考慮去除頭狼作用,保留其他算法機制. 采用實數編碼方式生成可行拆卸序列,通過對算法操作進行離散化操作,并引入反向學習策略跳出局部最優,通過Pareto解集和NSGA-Ⅱ擁擠距離機制評價非劣解集,引入精英保留策略加快算法向全局最優解靠攏.
2.1 編碼及解碼設計
在拆卸線設計過程中通過人工識別確定零部件的組成結構、拆卸作業時間、危害和需求屬性等拆卸信息,并整合形成優先關系矩陣P和拆卸信息矩陣B,以便作為算法求解計算所能識別處理的問題參數輸入,在滿足特定約束條件下通過編碼操作生成可行解,通過解碼操作將拆卸任務合理分配到各工作站內并計算目標適應度值,為實現廢舊產品的大規模拆卸奠定數據基礎.
采用基于實數編碼方式生成可行拆卸序列,將優先關系矩陣P中無緊前約束任務放入可選任務集中,隨機挑選其中的一個任務i放入當前拆卸序列位置m中,將P中任務i所在行全部置為0,以釋放對其他任務的約束關系,同時將任務i所在列全部置為1,以加強自身約束,保證不會重復選取到該任務,然后m=m+1,重復以上步驟,直至所有任務均分配完成,由此得到的實數序列即為可行拆卸序列.
由于在U型不完全拆卸過程中,并不是所有任務都需要進行拆卸,只要零部件存在需求性或危害性這兩種特性中的其中一個,就必須要拆卸該零部件,但也會存在某一個零部件同時存在需求性與危害性的情況,在解碼時僅需確保必須拆卸零部件總數滿足要求即可,不會影響算法性能. 因此,將解碼過程分為兩個階段,第一階段是得到實際需要拆卸的任務序列,第二階段是將所得的拆卸序列在滿足所有約束情況下分配到工作站中,具體步驟如下:
步驟1輸入可行拆卸序列X,計算拆卸產品中必須拆除的零部件總數Nnum,設置開啟工作站序號ks=1,工作站空閑時間TR=TC,危害性或需求性零部件計數iex=1;
步驟2從解序列位置編號m= 1開始遍歷X,若某位置m上的任務i∈{i|di+hi≥1},則iex=iex+1;若iex=Nnum,則將對應位置編號m及之前的序列單獨取出,作為新的不完全拆卸序列Yp輸出,序列長度為l,解碼第一階段完成;
步驟3初始化序列位置編號,入口位置p=1,出口位置q=l;
步驟4判斷位置p、q上的任務i、j的作業時間是否小于當前工作站空閑時間TR,若條件成立,則將滿足條件的任務放入可分配任務集合S中;
步驟5確定可分配任務集合大小NS,num,若NS,num=0 ,則開啟新的工作站ks=ks+1 ,重置空閑時間TR=TC;否則將拆卸作業時間較長的零部件作為待分配任務;
步驟6確定待分配任務的編號,若為i,則分配到入口側,p=p+1 ;否則,分配到出口側,q=q?1; 修改工作站剩余空閑時間TR=TR?ti;
步驟7重復步驟4~6,直至序列Yp中任務分配完畢.
2.2 “輪盤賭”選擇操作
本文采用“輪盤賭”法進行種群劃分,根據個體適應度值計算個體選擇概率及累加概率選取As匹人工狼組成探狼群,具體計算如下:
式中:NW為種群規模;f(Xi)、p(Xi)分別為第i個個體Xi的適應度值和選擇概率;P(Xi)為累加概率,其值越大,個體選中機率越大,由此選擇探狼個體.
2.3 自適應游走行為
探狼在解空間內朝R個方向分別進行游走搜索獵物,根據獵物氣味濃度(可認定為目標適應度值)自主決策前進方向,具體表示為

式中:xie,r為探狼i在第e(e= 1,2,···,E)維空間朝第r(r= 1,2,···,R)個方向前進后的位置;xie為探狼i在第e維空間的位置;sa為游走步長.
為了使算法在迭代前期擴大全局搜索尋優能力,同時在迭代后期有更大概率朝全局最優解靠攏,加強穩定性. 考慮隨著迭代次數的增加,減少游走方向數R,加快算法收斂速度. 計算方法如下:
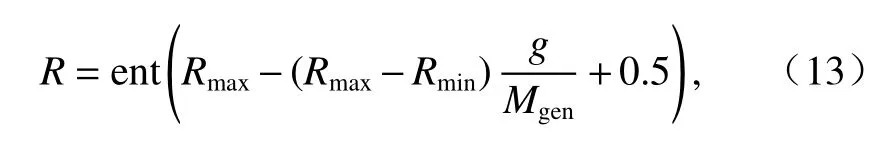
式中:Rmax、Rmin分別為游走方向數的最大、最小值;g為當前迭代次數;Mgen為算法最大迭代次數.
結合DLBP編碼特點,設計一種基于隨機擾動的自適應游走行為,產生若干鄰域解,具體步驟如下:
步驟1輸入拆卸序列X,設置游走次數kt= 1,游走方向計數r= 1,游走次數閾值為kt,max,根據式(13)計算游走方向數R;
步驟2生成表示序列位置的隨機整數u(u∈{1,2,···,U}),確定u上的任務編號iask;
步驟3利用優先關系矩陣確定iask相鄰的緊前任務Ptask和緊后任務Stask,將緊前緊后任務間的序列作為可操作序列片段Yo;
步驟4生成與序列Y相同長度的單調遞增隨機數組,將iask對應的隨機數rnum按式(12)進行計算,并將隨機數組按遞增順序重排,對應的iask位置發生變動,生成新的序列片段Z;
步驟5用序列片段Z代替Yo,放入序列X中,生成新的鄰域解XNew并保存,更新游走方向計數r=r+1;
步驟6若r 步驟7若kt 結合DLBP實際特點,利用基于交叉操作接收召喚信息,并通過生成隨機整數確定變異點,基于變異操作執行猛狼向頭狼奔襲行為. 具體步驟如下: 步驟1輸入探狼序列X,猛狼序列Y,生成兩個表示序列位置的隨機整數p、q; 步驟2確定序列Y中位置p、q間的序列片段Z,并遍歷序列X,若某位置上的任務編號在序列Z中存在,則依次存放到新的序列片段ZNew中; 步驟3用ZNew替換Y中原拆卸序列片段Z,生成新的拆卸序列YNew1,完成召喚信息傳遞; 步驟4生成表示拆卸序列位置的隨機整數m,確定YNew1中該位置的任務編號iask; 步驟5根據優先關系矩陣確定iask在YNew1中的相鄰最近的緊前緊后任務位置a、b,將位置a和b之前的序列除去iask作為可操作序列,在其中隨機插入iask,由此生成新的拆卸序列YNew2; 步驟6比較拆卸序列Y、YNew1及YNew2的適應度值,更新猛狼位置. 為快速收斂,本文考慮將單個目標最優的人工狼作為驅動解按式(14)執行圍攻行為,為算法每次的迭代尋優提供單目標參考值. 式中:λ為 [?1,1]間的隨機數;sc為圍攻步長;和分別為第k次迭代時人工狼與獵物在第e維空間所處位置. 步驟1計算交換序列對數ENum,生成ENum個不大于拆卸序列長度N的互不相等的隨機整數,用以確定交換對位置集EPos; 步驟2根據EPos逐個確定G、xi對應位置上的任務交換對{GTask,xi,Task}; 步驟3基于DLBP實數編碼的特點,同一任務有且僅能分配一次,因此確定GTask在拆卸序列xi中的位置,并交換序列對GTask與xi,Task的位置; 步驟4判斷交換序列對位置后是否滿足優先關系約束,條件成立的交換對如圖2中實線表示的交換對{5,4}、{3,2},將其予以保留,將不滿足條件的如圖2中虛線表示的交換對{10,7}舍棄. 圖2 目標驅動圍攻行為Fig. 2 Goal-driven besieging behavior 反向學習策略[17]基本思想是為擴大種群搜索范圍,基于當前個體在可行域范圍內生成一個對應的反向解個體,比較兩個個體的適應度值,選擇較優的個體進入下一次迭代優化. 具體定義如下:設解Xi={xi1,xi2,···,xie}為e維空間中的一個可行解,xie為第e維空間的變量,其定義域為 [ae,be], 式中:rn為 [0,1] 間的隨機數. 在滿足DLBP優先關系約束情況下,生成人工狼反向種群,從中挑選適應度值較優的人工狼替換原種群中較差的個體,保證種群的優越性. 由于DLBP問題涉及多個量綱不同的目標優化,不能簡單的將其轉化為單目標問題求解,同時缺少決策者的個人偏好等關鍵信息,需要采取先優化再決策的方式,因此考慮引入Pareto解集理論獲得多個具有不同側重點的非劣解. 對于最小化多目標優化問題,給定兩個可行解X1、X2,其第w個目標適應度值分別為fw(X1),fw(X2),若滿足式(16)則稱解X1Pareto支配解X2,記為X1?X2. 本文考慮采用基于外部檔案的精英保留策略,將每次迭代尋優獲得的Pareto解存放于外部檔案中,并不斷更新外部檔案,使算法加速朝全局最優解收斂. 當非劣解個數超過設置的外部檔案容量時,通過NSGA-Ⅱ擁擠距離機制[19]篩選去除部分非劣解.定義邊界個體的擁擠距離為∞,其余解X對應的單目標值fw(X)分別按升序排列后,計算如式(17)所示. 式中:L(X)為解X的擁擠距離;Xg?1、Xg+1分別為X排序前、后的解. AOBL-MWPA具體算法流程如圖3所示. 圖3 BL-MWPA算法流程Fig. 3 AOBL-MWPA flowchart 在硬件配置為Intel(R) Core(TM) i5-9500 CPU,3.00 GHz主頻,8.00 GB內存的計算機上,通過Win10系統上的MATLAB 2018開發算法程序. 為驗證所以算法的性能,將其應用于不同規模的算例中求解計算,并與現有文獻中的算法結果進行對比. 通過文獻[20]的19個基準算例來驗證AOBLMWPA算法的性能,定義任務拆卸數量N為首項為8,公差為4,末項為80的一組等比數列,不考慮零部件間的優先關系約束,任務拆卸作業時間ti∈{3,5,7,11} ,節拍時間TC= 26 s,定義最后一個作業時間為11 s的任務為危害性零部件,最后一個作業時間為7 s的任務為需求零部件. 優化目標有:最小化工作站數量f1、最小化空閑時間均衡指標f2、最小化拆卸深度f3及最小化拆卸成本f4,同時附加計算求解時間進行對比說明. 現有文獻中的求解算法有蟻群算法(ant colony optimization,ACO)[20]、改進蟻 群算法(improved ant colony optimization,IACO)[15]、多目標免疫機制協作遺傳算法(multi-objective immune mechanism cooperative genetic algorithm,MIGA)[21]及變鄰域搜索算法(variable neighborhood search,VNS)[14]. 通過正交試驗設計確定算法參數,因篇幅問題不展開說明,從求解時間和求解質量兩方面綜合考慮,設置算法參數為NW= 60,Mgen=120,sa=1.5,kt,max= 8,計算對比結果如圖4所示. 圖4 19個基準算例對比結果Fig. 4 Comparison results of 19 benchmark instances 由基準算例的構造方法可得,真實Pareto前沿解最優結果為{N/4,0,1,2}或{N/4,0,2,1}. 通過對所提算法和現有文獻求解結果的均值進行對比,在工作站數量f1和空閑時間均衡指標f2上,所提AOBLMWPA算法和MIGA算法在小規模(N≤20)上均能求解到最優解f1=N/4,f2= 0,但在中規模(20 現以某型報廢汽車為對象,分析AOBL-MWPA算法在U型不完全拆卸線方案規劃中的應用情況.現獲得的拆卸信息包括零部件拆卸作業時間t(s),危害屬性h,需求屬性d,單位時間作業成本C(元/s),具體如表1所示,優先關系如圖5所示. 圖5 某汽車拆卸優先關系Fig. 5 Disassembly precedence relations of a car 表1 某汽車拆卸信息Tab. 1 Disassembly information of a car 根據實際生產情況,設置其生產節拍TC= 640 s.經過正交試驗測試計算,綜合考慮算法求解精度和求解時間,確定算法參數為NW= 60,Mgen= 120,sa=1.5,Tmax= 8,外部檔案大小NQ= 10. 算法運行求解10次,取其中較好的一次結果如表2所示,拆卸方案中帶負號的編號零件表示該零件在U型出口側進行拆卸作業,反之,則在U型入口側進行拆卸作業. 通用工作站需要對入口側與出口側的產品進行拆卸作業,專用工作站只需對流水線某一側待拆產品進行作業. 從表2結果看出,根據Pareto解集思想,所提算法能求解得到10個非劣解,開啟的工作站數量均為9個,拆卸零部件數量為38個,空閑時間均衡指標變化范圍為28.142 5~33.015 1 s,拆卸成本變化范圍為381.946 4~387.954 9 元/s,因此決策者可根據實際情況選擇合適的拆卸方案,若決策者注重空閑時間均衡指標可選用方案2,該優化目標為28.142 5 s;若決策者注重企業的拆卸成本,則可選擇方案1,最小成本為381.946 4元/s. 表2 U型汽車拆卸線任務分配方案Tab. 2 Task allocation plan for U-shaped car disassembly line 1)本文結合企業實際情況,對U型不完全拆卸線平衡問題展開研究,構建了以最小化工作站數量,空閑時間均衡指標,拆卸深度和拆卸成本為優化目標的數學模型. 2)針對問題特點,設計一種自適應反向學習多目標狼群算法,為兼顧算法前期的全局搜索能力和后期的穩定性,提出改進的自適應游走行為,同時引入反向精英學習策略有效避免算法陷入局部最優解,利用Pareto解集思想和NSGA-Ⅱ擁擠距離篩選評價機制,實現不同側重點的精英解集的保留,指導算法搜索尋優方向,同時加快算法收斂速度. 3)通過將所提算法應用于不同規模問題的19個基準算例,并與現有文獻中的求解算法進行對比,結果表明所提算法在不同評價指標上的求解結果優于其他算法,驗證了其求解性能更優. 最后,將所提算法應用于采用U型布局不完全拆卸方式的具有40項任務的某汽車拆卸實例中,求解獲得10個Pareto非劣解,為決策者提供了廣泛的決策空間,驗證了所提算法和模型的正確性和有效性. 致謝:中車“十四五”科技重大專項課題(2021CHZ010-3).2.4 召喚行為
2.5 目標驅動圍攻行為
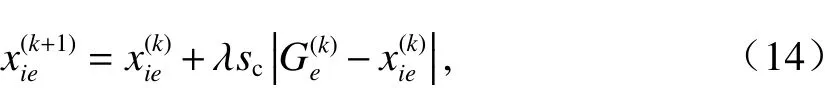

2.6 反向學習策略

2.7 多目標處理方法
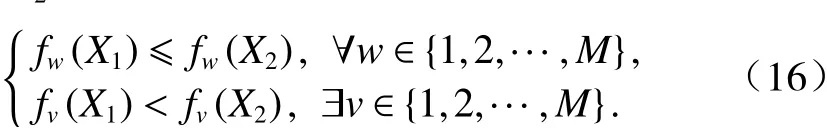
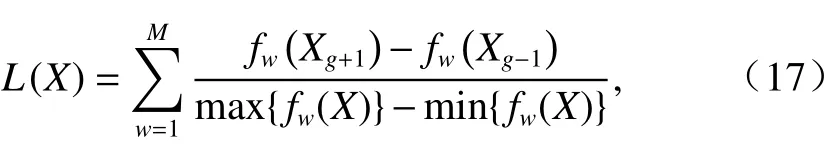
2.8 算法流程

3 算法性能驗證和實例應用
3.1 基準算例驗證
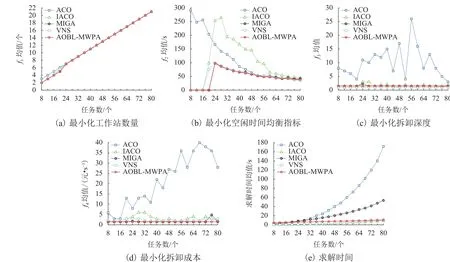
3.2 實例應用



4 結 論

