TOPSIS在山區鐵路線路方案比選中的二次改進

李遠富 ，蔣 頻 ，樊 敏 ，樊惠惠 ，吳文芊 ，楊昌睿

（1. 西南交通大學土木工程學院, 四川 成都 610031；2. 西南交通大學高速鐵路線路工程教育部重點實驗室, 四川成都 610031）

有許多山區鐵路項目已納入規劃或是正在建設，山區干線鐵路、高速鐵路等的規劃與建設將為我國優化干線鐵路網布局，推進高速鐵路“八縱八橫”主通道建設，拓展鐵路網覆蓋范圍以及拉動山區經濟增長打下堅實基礎.

山區地形困難、地質復雜、生態脆弱且城鎮經濟據點稀少，因此山區鐵路線路方案比選更加注重工程的安全性、地質選線原則、綠色環保理念以及對沿線經濟發展的帶動效果等[1]. 在此之前，國內已有眾多學者就山區鐵路線路方案比選做了大量研究：羅圓[2]將鐵路選線視為帶有不確定性的多目標決策過程，分別將可靠性數學理論、風險分析理論和效用理論等運用于山區鐵路線路方案評價，提出基于不確定性分析的山區鐵路線路方案評價方法；鄧漢軒[3]突出山區鐵路線路方案優選過程中的環境因素，在運用西部山區鐵路選線工程實例的基礎上，比較模糊綜合評價和人工神經網絡評價兩種方法，最終得出人工神經網絡評價法的效果更好；林凱[4]在進行困難艱險山區高速鐵路線路方案綜合優化研究時，將防災救援部分考慮進去，建立考慮防災救援的困難艱險山區高鐵線路方案綜合優化模型；張明威[5]分析了多嶺和強震山區的鐵路建設風險，歸納出強震山區越嶺鐵路的選線策略，同時結合層次分析法與熵權法，構建強震山區越嶺段鐵路線路方案風險評價模型.

TOPSIS （technique for order of preference by similarity to an ideal solution）是由Hwang和Yoon在1981年提出的一種用于解決單一型或混合型多屬性決策問題的方法[6]，其主要優點是便于理解、計算較簡單、適用范圍廣、幾何意義直觀等. 但TOPSIS有兩個較為突出的不足之處：無法消除決策問題中屬性指標間的相關性影響；計算雖簡單，但需額外的規范化和賦權手段來分別解決屬性指標量綱不一致和權重分配的問題，這不免會使決策過程復雜化. 而且當采用主觀賦權手段時，決策結果的可信度將降低，當采用主客組合賦權手段時，決策過程將進一步復雜化.近年來，國內外學者對TOPSIS的改進研究非常多樣化：Jahanshahloo等[7]運用區間數來改進TOPSIS，并提出一種基于區間數的TOPSIS決策問題擴展算法；Dymova等[8]采用區間2型模糊值的alpha分割來彌補TOPSIS在進行2型模糊擴展時的不足，且經實例證明此2型模糊擴展不受已知方法的限制；王先甲等[9]以馬氏距離代替歐氏距離來改進TOPSIS，最終達到消除變量間相關性干擾的目的；Wang等[10]將基于五級法改進的AHP （analytic hierarchy process）作為TOPSIS的額外賦權工具，由此構建油氣管道客觀風險綜合評估模型.

就多數對TOPSIS的改進研究而言，一些將改進重點放在決策環境的拓展上，一些注重對賦權方式的完善，另一些從屬性指標中的不確定性信息著手加以改進，還有一些就方法本身的單個缺陷做相應改進，但鮮有學者同時兼顧上述4個方面，并且彌補TOPSIS的兩個不足. 本文先以馬氏距離代替TOPSIS中的歐氏距離，以相關系數矩陣代替馬氏距離中的協方差矩陣，實現TOPSIS的二次改進，既彌補了TOPSIS的兩個不足，完成對屬性指標的客觀賦權，又解決了協方差可能導致的問題；然后運用區間數和云模型實現從定性語言到定量表示的過渡，既充分考慮了屬性指標的不確定性和離散性，又很好地克服了評價方法在處理模糊性和隨機性方面的不足；最后將上述方法及模型應用于山區鐵路選線決策環境，決策結果表明該方法及模型科學、有效，可為日后解決類似決策問題提供一定的參考.

1 TOPSIS及其改進分析

1.1 TOPSIS的步驟

假設有m個備選方案A1、A2、···、Am和n個屬性指標C1、C2、···、Cn.xij為Ai在Cj下的指標值（i=1，2，···，m；j=1，2，···，n）. TOPSIS的步驟如下：

步驟1根據屬性指標值構造的決策矩陣為

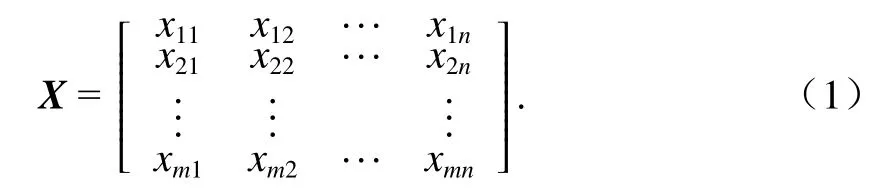
步驟2進行規范化處理，消除決策矩陣中數據量綱不同帶來的影響，處理后得到的標準化矩陣為

步驟3確定權重W=diag(w1，w2，···，wi，···，wn)，權重滿足與標準化矩陣相乘，得到的價值矩陣為

步驟4確定正理想方案S+和負理想方案S?：求解方法如下：

當Cj為效益型指標時：

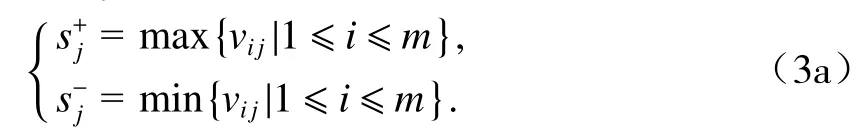
當Cj為成本型指標時：

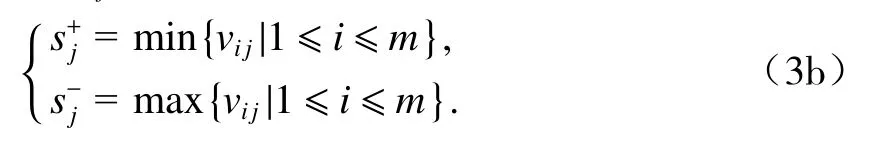
當無步驟2和步驟3時，將式（2）、（3）中的vij替換成xij即可.

步驟5分別計算Ai到S+的歐氏距離Di+，Ai到S?的歐氏距離Di?. 如式（4）.

步驟6計算各備選方案的相對貼近度. 求解方法如下：

步驟7根據Ci*的大小進行相對優劣排序，顯然Ci*∈[0，1.0]. 對式（5a），Ci*越大越優；對式（5b），Ci*越小越優.

1.2 TOPSIS第一次改進

1.2.1 TOPSIS的局限性分析

1） 由于歐式距離本身的局限性，當指標間存在相關性，指標所包含的信息重疊，歐式距離失效，決策結果不準確. 而現實決策問題的屬性指標幾乎都存在相關性，所以這一問題必須得到解決.

2） 屬性指標的量綱通常不一致，TOPSIS會因量綱不一致而失效，而歐氏距離不能消除量綱不一致帶來的影響，需要借助額外的規范化手段來消除，使決策過程復雜化. 1.1節中的步驟3是各屬性指標的賦權過程，需要借助額外的賦權手段才能完成，如果采用主觀賦權手段確定權重，決策結果的可信度會降低，如果采用主客組合賦權手段確定權重，由于組合賦權過程本身就很繁復，決策過程將進一步復雜化. 因此，上述兩個方面是亟須改進的[11].

1.2.2 TOPSIS的改進思路

馬氏距離是由印度統計學家Mahalanobis在1936年提出的一種統計距離. 相對于歐氏距離，馬氏距離對屬性指標的變化敏感，獨立于測量尺度，更能體現各狀態或特征間的關系，并且還能排除指標間不同程度的相關性干擾. 同時馬氏距離是以標準差函數計算指標權重的，指標值變化大的內化權重賦值小，克服了在計算距離時指標變化程度不同但起相同作用的缺點.

本文利用馬氏距離本身能有效排除指標間的相關性干擾、不受量綱影響以及內化于公式的客觀賦權方式的優良特性，以馬氏距離代替歐氏距離來實現TOPSIS的第一次改進. 改進后的TOPSIS不僅可以排除指標間的相關性干擾，而且可以省略1.1節中的步驟2和步驟3.

1.3 TOPSIS第二次改進

1.3.1 馬氏距離的局限性分析

馬氏距離考慮的是屬性指標間的協方差，協方差是依賴量綱的量，且其大小代表的是兩屬性對各自均值偏差的綜合程度，故協方差可能導致計算結果不穩定，極易放大屬性間的影響，不能準確代表屬性間的關聯程度的問題[12]. 馬氏距離在TOPSIS中的表達式為

1.3.2 TOPSIS的改進思路

任意兩個隨機變量x、y的相關系數ρxy與協方差cov(x，y)的根本區別在于，當描述其關聯程度時前者不受量綱的影響，后者受量綱的影響，而且前者的描述過程更穩定，結果更準確[13]. 因此，以相關系數矩陣Q代替協方差矩陣Σ來改進馬氏距離，能解決協方差可能導致的問題. 將對馬氏距離的改進作為對TOPSIS的第二次改進，再次改進后的TOPSIS相比第一次改進更具科學性和有效性.

2 方案比選指標探討

2.1 指標選用

山區鐵路線路方案比選需要考慮的指標多而涉及面廣，指標選用時的側重點和標準均有所不同. 本文確定指標體系的遞階結構由總目標層、宏觀目標層和微觀目標層組成，在總結眾多其他學者研究成果的基礎上，秉承系統性、實用性以及定性與定量相結合等指標體系構建原則，從山區鐵路線路方案與技術經濟條件、周遭環境以及社會意義等大系統的協調發展出發，構建如表1所示的山區鐵路線路方案比選指標體系. 表1中的指標主要用于原則方案的比選，在進行實際方案比選時，可根據具體情況選擇相應的指標重新構建指標體系[14-15].

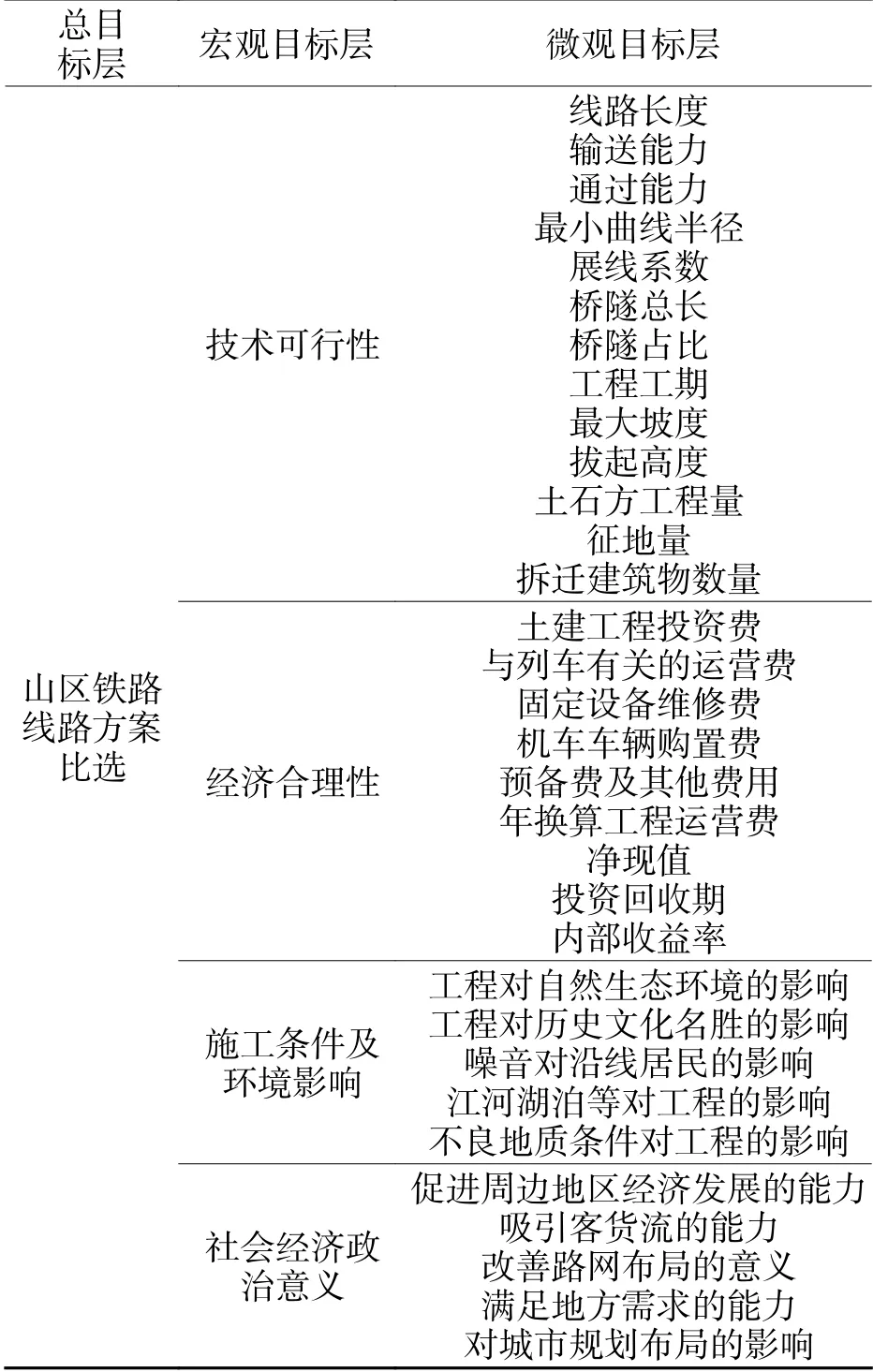
表1 山區鐵路線路方案比選指標體系Tab. 1 Index system of optimal selection of mountain railway location design

2.2 定性指標處理

山區鐵路線路方案比選指標體系中既有定量指標，又有定性指標. 定量指標直接采用精確數量化，定性指標的常用量化方式有區間數、三角模糊數和云模型，其中區間數只能部分考慮定性語言的不確定性特征，三角模糊數中3個變量的權重值相等，故其并未體現出變量的重要性. 本文先采用語言類模糊數表示定性指標，然后采用區間數作為語言類模糊數的轉化形式，最后運用云模型將區間數轉化為精確數，該精確數即作為定性指標值.

2.2.1 區間數

Moore在1965年首次提出區間數的概念. 區間數的獲得無需較多的假設和先驗知識，能便捷地表示數據中的不確定信息，而且在求解不確定性問題時能減少主觀因素的影響. 當某個問題的原始特征存在不確定性，且在給定的范圍內時，就可以用區間數來表示[16].

S={很好，好，較好，一般，較差，差，很差}或{很大，大，較大，一般，較小，小，很小}為語言類模糊數集. 定性語言“很好或很大”即為語言類模糊數，其本身存在一定的不確定性特征[17]. 區間數與語言類模糊數的轉化關系如表2所示.

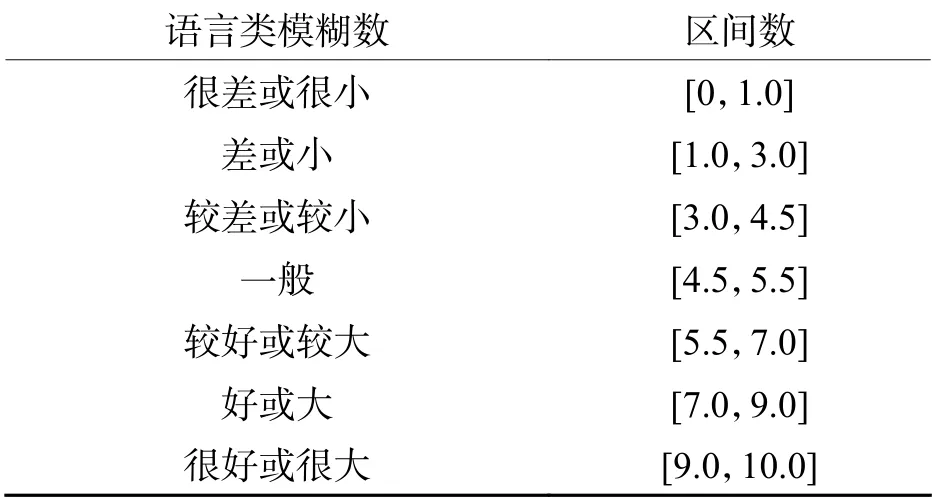
表2 語言類模糊數與區間數的轉化Tab. 2 Conversion between linguistic fuzzy number and interval number

2.2.2 云模型概述

云模型是由李德毅院士以概率統計和模糊數學為基礎提出的一種定性語言與定量表示間不確定性的轉換模型. 云模型不僅能充分考慮定性語言的不確定性和離散性，實現其與定量數值間的相互轉換，而且克服了評價方法在處理模糊性和隨機性方面的不足. 正態云模型是最基本也是最常用的云模型[18]. 設

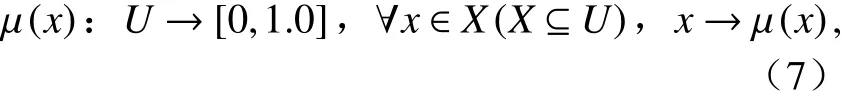
為論域U中的任意一個元素x對定性概念T的隸屬度，云即μ(x)在U上的分布. 其中，x為云滴，是云的最基本組成元素，也是定性概念T的一個量化值.

每個定性概念都可以用云的期望Ex、熵En與超熵He來定量表示，這3個數值稱為云模型的數字特征，記作C(Ex，En，He). 其中：期望Ex表示定性語言量化為云滴群的中心點，是最能代表某一定性語言的取值；熵En反映了云滴群分布的不確定性；超熵He表示定性語言量化為云滴群的離散性[19].

2.2.3 正向云、條件云發生器

云模型發生器包括正向云發生器、逆向云發生器和條件云發生器. 正向云發生器是由定性語言向定量數值轉換的映射，即對定性語言的量化算法. 正向云發生器輸入的是需要轉換的定性語言的3個數字特征，輸出的是n個云滴—— d rop(xt,μt). 正向云發生器算法如下：

步驟1生成正態隨機數E′nt=NORMRND(En，(He)2) ，其中En和 (He)2分別為期望和方差；

步驟2生成正態隨機數其中為方差；

步驟3計算即為數域中任意一個云滴；

步驟4重復前面3個步驟，直到產生滿足條件的云滴或者設定的n個云滴為止.

條件云發生器分為X條件云發生器和Y條件云發生器，均以云模型的不確定性推理為基礎，結合正向云發生器實現由定性語言向定量數值的轉換. 由于通過發生器產生的云滴與輸出值均不唯一，也即不確定，故形成不確定性推理. 當定性規則描述成“如果C1，那么C2”，則C1和C2均為U中的定性概念，也是不確定性推理規則的前件云與后件云，該定性規則即為單條不確定性推理規則. 不確定性推理算法如下：

輸入：前件云C1的 期望ExC1、熵EnC1、超熵HeC1和特定數值x0以及后件云C2的期望ExC2、熵EnC2、超熵HeC2. 輸出：對應于前件云生成確定度為 μt的后件云定性語言的定量數值y01. 具體步驟為

步驟1由X條件云發生器生成正態隨機數其中分別為期望和方差；

步驟2由X條件云發生器計算x0在定性語言C1上 的確定度，

步驟3由Y條件云發生器生成正態隨機數

步驟4在Y條件云發生器內，如果x0激活C1的上升沿，則C2用上升沿計算y0. 即當x0≤ExC1時，

步驟5在Y條件云發生器內，如果x0激活C1的下 降 沿，則C2用 下降 沿 計 算y0. 即當x0>ExC1時，

3 基于二次改進的TOPSIS的山區鐵路線路方案比選步驟

步驟1確定參與比選的m個山區鐵路線路方案A1，A2，···，Am和n個屬性指標C1，C2，···，Cn中，Cj（j=1，2，···，k）為定量指標，Cj（j=k+1，···，n）為定性指標.xij為Ai在Cj下的指標值，定量指標值取用各方案提供的精確數.

步驟2先聘請專家用語言類模糊數給定性指標賦值；接著對照表2選取相應的區間數；然后由式（8）將區間數轉化為云模型的數字特征（云模型數），如表3所示，其中7個云模型數為不確定性推理算法中前件云的定量表示；最后采用百分制數值來表征定性指標因子水平的高低，水平越高，因子分值就越大. 分值大小的定性評語與相應的百分制云模型描述如表4所示，其中7個云模型描述為不確定性推理算法中后件云的定量表示.

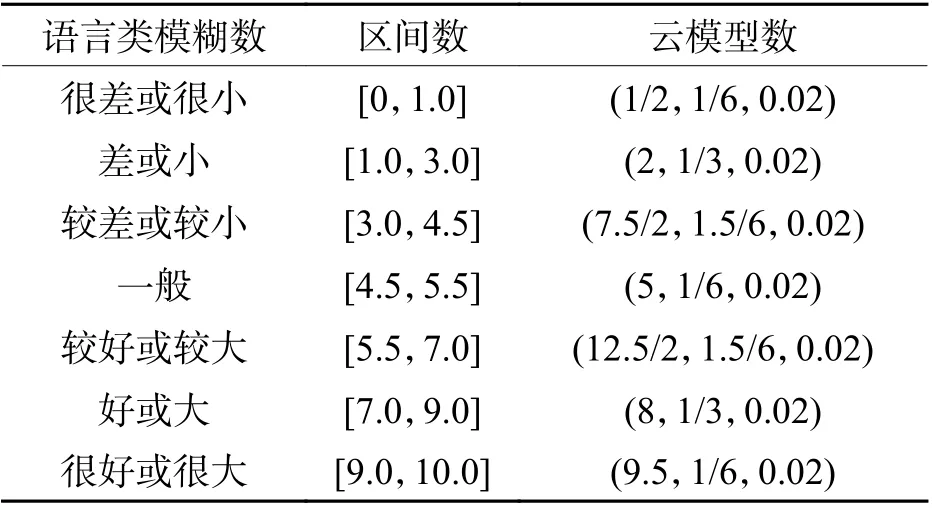
表3 語言類模糊數、區間數與云模型數的轉化Tab. 3 Conversion among linguistic fuzzy number,interval number and cloud model number

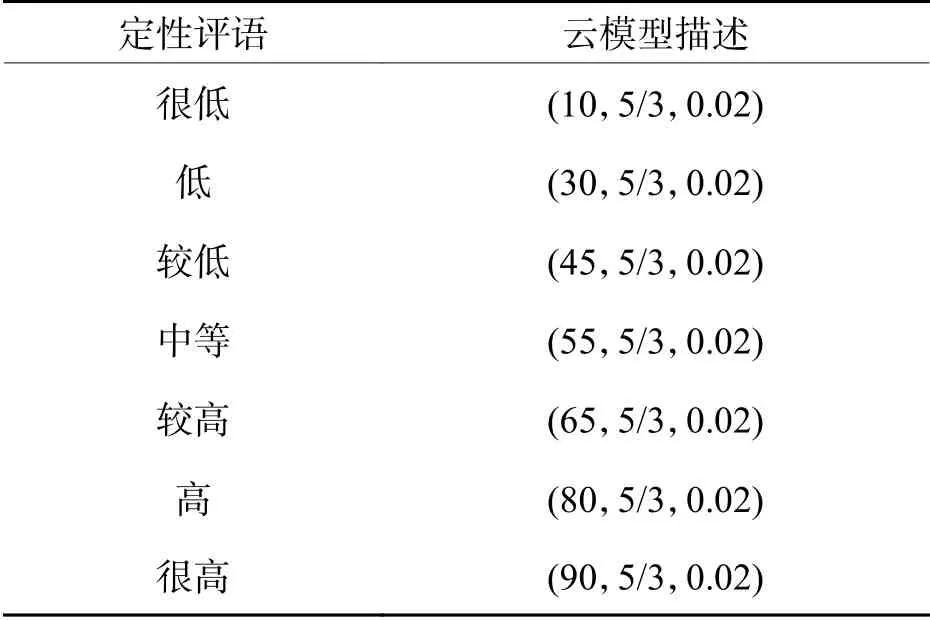
表4 定性評語與云模型描述的轉化Tab. 4 Conversion between qualitative comment and cloud model description

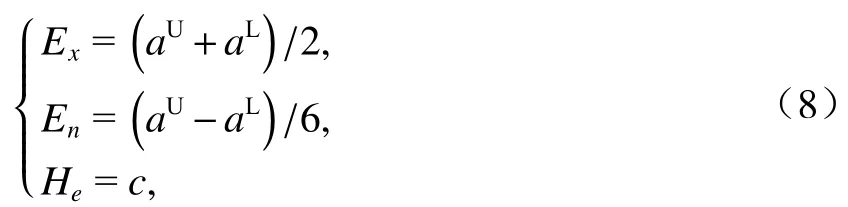
式中：c為常數，與語言類模糊數的本身離散程度和模糊度有關，一般取0.02.

以定性指標“改善路網布局的意義”為例，由專家知識構建語言類模糊數、定性評語和云模型描述間的不確定性推理規則. 當改善路網布局的意義“很小”，則定性評語為“很低”，云模型描述為（10，5/3，0.02）；當改善路網布局的意義“小”，則定性評語為“低”，云模型描述為（30，5/3，0.02）.以此類推.

步驟3運用云模型發生器獲得由精確數表示的定性指標值，具體操作如下：

首先由表3中的7個云模型數驅動正向云發生器，將生成的7個正態隨機數xt的均值作為X條件云發生器的特定數值x0；隨后將x0和實際方案Ai的某一定性指標的對應云模型數代入X條件云發生器，即執行2.2.3節中不確定性推理算法的步驟1、2，得到相應的確定度 μt；最后將 μt和通過不確定性推理規則確定的云模型描述作為Y條件云發生器的輸入，激活后隨機產生云滴 d rop(y0,μt)，即執行不確定性推理算法的步驟3、4或5，精確數y0即作為該定性指標的取值.

步驟4由上述步驟確定的所有指標值構造方案比選的決策矩陣，如式（1）.

步驟5根據二次改進的TOPSIS求得相對貼近度，并根據相對貼近度的大小進行方案的相對優劣排序. 對式（9a），越大越優；對式（9b），越小越優.

4 實例分析

結合某山區鐵路巴塘至昌都段局部線路走向方案，對比分析由本文方法及模型得到的比選結果與實際工程的優選結果，以說明該方法及模型的科學性與有效性.

該鐵路巴塘至昌都段位于橫斷山脈中部，線路起于海子山西麓，在跨金沙江、穿芒康山脈、跨瀾滄江后，止于昌都市. 區域交通主要由G214、G317、S501、巴白路等組成. 沿線政治經濟據點坐落不一，交通狀況錯綜，地形地質復雜，自然環境自我修復能力較弱. 根據沿線政治經濟據點分布、交通狀況以及地形地質條件等因素，研究了經白玉、江達，經白玉、貢覺、江達，經白玉、貢覺，經貢覺、江達和經貢覺取直五大線路走向方案.

通過綜合分析，選用表5所示的9個指標進行線路方案綜合比選（取值根據該山區鐵路的預可行性研究報告的相關內容確定）. 其中：A1～A5依次代表經白玉、江達，經白玉、貢覺、江達，經白玉、貢覺，經貢覺、江達和經貢覺取直五大線路走向方案；C1～C9依次為線路長度、橋隧總長、工程靜態投資、年換算工程運營費、對自然生態環境的影響、不良地質條件對工程的影響、促進周邊經濟發展的能力、改善路網布局的意義、滿足地方需求的能力9個指標，前6個為成本型指標，后3個為效益型指標.

運用正向云發生器、條件云發生器以及不確定性推理機制，將給定性指標賦值的語言類模糊數轉化為百分制數值，也即獲得由精確數表示的定性指標值. 運算過程由MATLAB實現，結果如表6所示.

表6 由精確數表示的定性指標值Tab. 6 Qualitative index value represented by exact number

由5個方案的所有指標值構造方案比選的決策矩陣X，并確定正理想方案S+和負理想方案S?，S+={204.711，188.375，254.251，318.326，55.010 7，8.762 3，88.762 2，88.755 8，88.763 4}；S?={274.562，242.171，330.298，416.236，81.685 8，55.010 7，45.536 2，55.010 7，64.494 6}

式（9a）計算值越大，則方案越優，因此不難得出方案A1最優. 對表5中的指標進行分析可知，雖然經白玉、江達方案線路長度較長，工程投資較多，但地質條件、交通條件、設站條件最好，而且該方案經過了玉龍銅礦，同時輻射范圍最廣、能更好地帶動地方經濟發展，滿足地方意見及其他要求. 如以所選擇的9個指標作為線路方案綜合比選的主要依據，則由本文方法及模型得到的比選結果與該項目的預可行性研究報告中建議選擇的結果較為一致，說明該方法及模型具有較好的科學性與有效性.

表5 線路走向方案及其屬性指標取值Tab. 5 Route direction scheme and its attribute index value

5 結 論

1） 現實決策問題的指標間幾乎都會存在相關性，指標的量綱會有差別，指標的賦權過程或不夠科學或過于復雜，這要么使TOPSIS的決策過程復雜化，要么使TOPSIS的決策結果不夠準確. 鑒于馬氏距離本身帶有能有效排除指標間相關性干擾等優良特性，以馬氏距離代替歐氏距離來改進TOPSIS，改進后的TOPSIS既能保證決策結果的科學性與準確性，又能使決策過程簡單化.

2） 馬氏距離在TOPSIS中的表達要考慮協方差. 在計算馬氏距離時，可能會因考慮協方差而導致不能準確代表屬性間的關聯程度等問題的出現.任意兩變量的相關系數能夠彌補協方差的不足，它能準確地描述變量間的關聯程度，而且描述過程穩定，描述結果準確. 故以相關系數矩陣代替協方差矩陣來改進馬氏距離，把對馬氏距離的改進作為TOPSIS的第二次改進，再次改進后的TOPSIS更加科學、客觀.

3） 語言類模糊數本身帶有一定的不確定性特征. 區間數的運算過程雖簡單、直觀，但其不足之處在于不能充分考慮定性語言的不確定性特征. 而云模型既能充分考慮定性語言的不確定性和離散性，又克服了評價方法在處理模糊性和隨機性方面的不足，還能實現由定性語言向定量表示的有效轉換. 所以本文選用云模型實現語言類模糊數的精確數化.

4） 針對二次改進的TOPSIS，在求算馬氏距離時需計算相關系數矩陣的逆. 本文實例分析中的相關系數矩陣存在逆矩陣. 但在極少數情況下，當屬性指標線性強相關時，相應的相關系數矩陣可能不可逆，此時馬氏距離將無法求算，進而無法得到決策結果. 要求相關系數矩陣一定可逆不太現實，但如何確保在推進決策工作時能求算出相關系數矩陣的“逆矩陣”是值得進一步研究的. 例如當相關系數矩陣不可逆時，可采用奇異值分解法求算其正定的“廣義”逆矩陣，以其代之.

5） 結合某山區鐵路巴塘至昌都段局部線路走向方案，由本文方法及模型得到的比選結果同實際工程的優選結果基本一致，說明該方法及模型具有較好的科學性與有效性，并為今后類似決策問題的解答提供一定的參考.