基于格子玻爾茲曼方法的二維柔性梁與剛性方柱相互作用的數(shù)值研究

楊旖旎，謝振武，鄒明松

（中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

帶流固耦合的復雜繞流，尤其是柔性體-剛體-流體耦合運動，在自然界中普遍存在，如魚類在海洋立管前后端的游動，以及日常生活中所見到的旗幟拍動等。柱體后加柔性絲線的流固耦合振動是流固耦合研究中的典型問題。Sui 等[1]對靜止圓柱尾流與無質(zhì)量柔性絲線的耦合干擾進行了數(shù)值模擬；Yildirim 等[2]發(fā)現(xiàn)了絲線運動方式對上游圓柱尾流的反饋影響；Jia 和Yin[3]通過肥皂膜流動的實驗發(fā)現(xiàn)，隨著絲線相對圓柱的位置變化，柔性絲線在尾流中呈現(xiàn)出三種典型的拍動響應模態(tài)；胡浪超等[4]采用罰浸入邊界/格子Boltzmann方法研究了旋轉(zhuǎn)圓柱尾流中的柔性絲線拍動模態(tài)。

與圓柱體后加柔性體的流固耦合問題相比，方柱后加柔性體的文獻記載更少。對于方柱振動問題，Bearmann 等[5]針對風洞中的方柱進行了實驗研究。Coeless 和Parkinson[6]發(fā)展了擬穩(wěn)態(tài)模型，模擬了方柱振動，并與實驗進行了對比。Zhao 等[7]數(shù)值模擬了低雷諾數(shù)下帶流向角的單方柱振動問題，研究發(fā)現(xiàn)：當流向角為0°時單方柱并無馳振現(xiàn)象，且鎖定區(qū)域較小；當流向角為22.5°和45°時有馳振，且鎖定區(qū)域明顯增大。Sharma和Dutta[8]通過實驗分別對帶有剛性和柔性板的固定方柱的流場結構特征進行了研究，發(fā)現(xiàn)板長的改變將引起尾跡的明顯轉(zhuǎn)變。涂昌健等[9]基于浸入邊界-譜元法數(shù)值模擬了方柱附加柔性懸臂梁流固耦合振動問題。

以往學者對于圓柱體后加柔性體的流固耦合問題較為關注，但是對低雷諾數(shù)下，方柱后附加柔性體的研究較少。為了進一步研究方柱后附加柔性梁對方柱振動的影響，本文對雷諾數(shù)Re=100 時，方柱質(zhì)量比mr=3，梁質(zhì)量比ms=0.3,彎曲剛度系數(shù)kb=0.0001時的方柱后附加柔性絲線的流致振動進行了數(shù)值研究，重點研究了方柱的振動幅值、振動頻率等振動響應特性隨折減速度的變化規(guī)律。

1 控制方程及其求解

1.1 格子波爾茲曼方法（Lattice Boltzmann Method,LBM）

與傳統(tǒng)CFD（Computational Fluid Dynamics）直接求解宏觀N-S（Navier-Stokes’）方程不同，LBM 通過求解離散玻爾茲曼方程：

得到流體的運動，是一種介觀方法。其中e為粒子速度，Ω(f)表示粒子的碰撞。

在LBM 中，流體被看成是規(guī)整格子上的流體粒子，用粒子分布函數(shù)fα表示，流體粒子按α個特定方向的粒子速度進行遷移和碰撞演化，最終得到所需要的流場信息。基于遷移和碰撞這一求解特性，LBM 具有計算簡單、并行效率高、邊界處理容易且易于耦合復雜外力場等優(yōu)點。LBM 中的離散速度模型一般記為DdQm模型，其中d表示維度，m表示離散速度數(shù)量。本文對二維數(shù)值研究采用了D2Q9模型（二維九速度模型），如圖1所示。

圖1 D2Q9模型Fig.1 D2Q9 model

選取單松弛碰撞模型Ω(f)= -(f-feq)/λ，通過離散方程（1）可得格子玻爾茲曼方程：

式（3）中，力項F采用Guo[10]等人提出的外力格式：

通過對分布函數(shù)求零階和一階矩，可得流體的宏觀密度、速度與壓力分別為

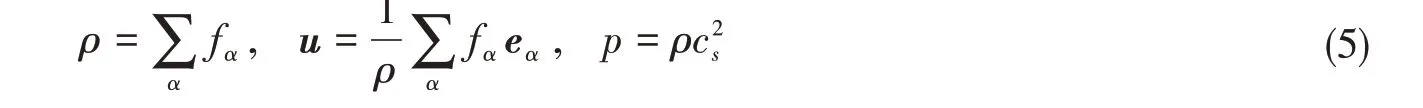
1.2 固體控制方程與數(shù)值方法

以流體密度ρ、來流速度U、梁長Lf為基本參考量，可得到柔性梁在拉格朗日網(wǎng)格下的控制方程：

對于第i(i= 0,1,2,...,n)個節(jié)點，張力項T可離散為

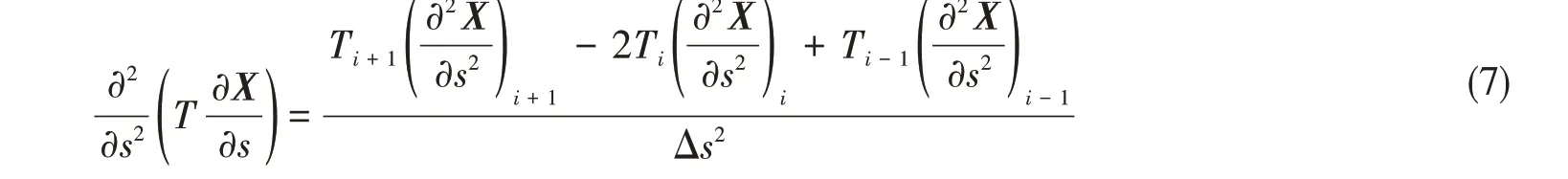
張力T由不可伸長條件確定，具體可參考文獻[11]。將T代入式(6)則可得到更新的梁位置坐標及速度。

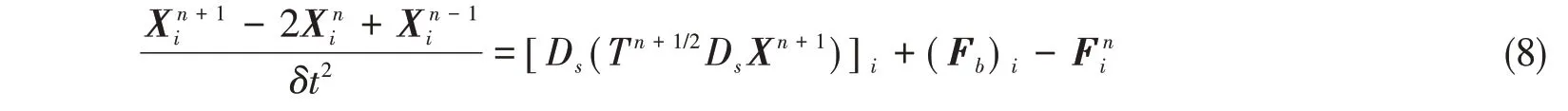
以流體密度ρ、來流速度U、方柱寬度D為基本參考量，單方柱運動控制方程可表示為

1.3 邊界處理

對于流固耦合邊界采用浸入邊界法處理。歐拉點上的速度傳播到附近拉格朗日固體點上的過程可表示為

拉格朗日力傳播到附近流體歐拉點上的過程可表示為

1.4 時間異步算法

圖2 時間步長比值隨時間的誤差變化Fig.2 Variation of time step ratio with time error

圖2中，dt為流體域所取時間步長，δt為結構域所取時間步長。由圖可以看出，當流體域步長與結構域步長比為50、100 時，計算誤差結果基本無差別。考慮到計算精度及計算效率的情況下，本文取時間異步算法的比值為dt/δt= 50。

2 計算參數(shù)設置以及數(shù)值驗證

2.1 計算參數(shù)設置

圖3 為方柱后附加柔性梁模型的簡化示意圖，入口給定一恒定速度U的均勻來流，雷諾數(shù)定義為Re=UD/υ。本文采用均勻網(wǎng)格，網(wǎng)格大小為0.02D，入口及上下邊界條件采用遠場邊界條件u=U,v= 0，出口邊界條件定義為紐曼邊界條件，即密度、速度沿軸向的梯度滿足?u/?x= ?v/?y= 0。選取計算域大小為[L×H]=[60D×24D]，此時邊界對計算結果影響可以忽略不計。方柱中心固定在[L/3,H/2]處。為了防止方柱與柔性梁發(fā)生碰撞，柔性梁固定端到方柱中心的距離G= 6D。

圖3 方柱-柔性梁系統(tǒng)結構示意圖Fig.3 Schematic diagram of square cylinder-flexible beam system

2.2 數(shù)值驗證

為了驗證本文計算方法的可靠性，本文對雷諾數(shù)Re= 100，質(zhì)量比mr= 3，流向角為45°的單方柱振動進行了數(shù)值模擬。Ymax=(Ay,max-Ay,min)/2 分別為方柱的順流、橫向無量綱振幅，其中Ay,max,Ay,min為方柱的最大位移和最小位移，fx,fy,fn分別為方柱順流向、橫向振動頻率及固有頻率。結果如圖4所示，本文計算結果與文獻[7]的結果吻合良好。

圖4 方柱流致振動結果驗證Fig.4 Verification of flow induced vibration results of square cylinder

為了與已有文獻結果作對比，本文對雷諾數(shù)Re= 100,kb= 0.0001,ms分別為0.22和0.28的梁拍動進行數(shù)值模擬。由圖5可以看出：當質(zhì)量比為0.22時，柔性梁在平衡位置附近震蕩后，幅值逐漸減小，最終達到靜止模態(tài)；當質(zhì)量比為0.28 時，柔性梁為穩(wěn)定的周期性拍動。因此，柔性梁由穩(wěn)定狀態(tài)到失穩(wěn)的臨界比在0.22～0.28之間，這與文獻[12]中ms= 0.26相吻合。

圖5 梁自由端位移時程曲線Fig.5 Displacement of a beam with free end position versus nondimensional time

3 結果與討論

3.1 方柱振動響應特性

對低雷諾數(shù)下Re= 100,D= 50,mr= 3,α= 45°,kb= 0.0001,ms= 0.3,Lf= 2D,G= 6D的方柱-柔性梁耦合系統(tǒng)進行數(shù)值模擬。為了防止方柱橫向位移過大與柔性梁發(fā)生碰撞，選取折減速度ur=3～17進行了模擬，對于每一種情況，都進行了足夠長的模擬時間以確保振動達到平衡態(tài)。

圖6為方柱的XY軌跡圖，圖7為方柱無量綱振幅Ymax=(Amax-Amin)/2和振動頻率比f=f/fn隨ur的變化曲線。由圖6～7可以看出：

圖6 XY軌跡圖Fig.6 XY-trajectory

圖7 方柱振動響應特性Fig.7 Response of the square cylinder with ur

（1）在鎖定區(qū)內(nèi)（3＜ur＜13），當ur＜11時，由于振動的不規(guī)則性，導致XY軌跡為非閉合環(huán)，隨著ur的增加（ur≥11），由閉合的雙相環(huán)逐漸發(fā)展為閉合單相環(huán)；在振動鎖定區(qū)外（ur＜5,ur＞13），當ur較小時（ur＜5），為對稱的‘8’字型單相環(huán)，當ur較大時（ur≥15），發(fā)展為不對稱的‘8’字單相環(huán)。

（2）方柱下游附加梁的振動依然以橫流為主，這與單方柱的振動類似。對任意梁長，隨ur的增加，方柱均出現(xiàn)了明顯的振動鎖定區(qū)，且鎖定區(qū)域大于單方柱情況下。

（3）在振動鎖定區(qū)內(nèi)，方柱的X、Y方向振動頻率比基本相等，且在1附近，在振動鎖定區(qū)外，X方向頻率比約為Y方向的兩倍。

圖8為不同折減速度下，方柱振動的位移時程曲線。當ur=5～11，方柱做明顯的不規(guī)則振動；當ur=13～15，方柱出現(xiàn)周期性振動，此時振動頻率接近于方柱的固有頻率，這是導致其振幅較大的主要原因；在ur=3,17時，方柱出現(xiàn)周期性振動，且振幅較小（＜0.5），X方向的振動頻率約為Y方向的兩倍。

圖8 方柱位移時程曲線Fig.8 Time histories of vibration displacement at different reduced velocities

圖9給出了方柱能量輸入、升力系數(shù)及橫向位移的時程曲線，其中Py=Cl,s(t)v(t)/U為方柱的無量綱功率。在振動鎖定區(qū)域外（圖9（a）、（e）），方柱的位移及升力系數(shù)隨時間推移呈穩(wěn)定的變化趨勢，且相位相反，此時升力對方柱的能量輸入穩(wěn)定。在振動鎖定區(qū)域內(nèi)，方柱平均升力系數(shù)不為零，此時方柱發(fā)生馳振（圖9（b）、（c）），位移與升力系數(shù)相位一致，方柱源源不斷地從外界吸收能量；在馳振區(qū)外（圖9（d）），方柱位移及升力系數(shù)呈穩(wěn)定的周期性變化，外界對方柱能量輸入穩(wěn)定，由于此時方柱振動頻率接近固有頻率，升力極易激勵方柱振動，致使方柱橫向產(chǎn)生較大位移。

圖9 方柱橫向位移、升力系數(shù)、能量輸入時程曲線Fig.9 Time histories of the lateral displacement,lift coefficient and energy input

3.2 流動結構特征

圖10分別給出了在方柱最大位移，ur= 3～17時的瞬時渦量圖。由圖可以看出系統(tǒng)的間距流態(tài)主要分為三種：

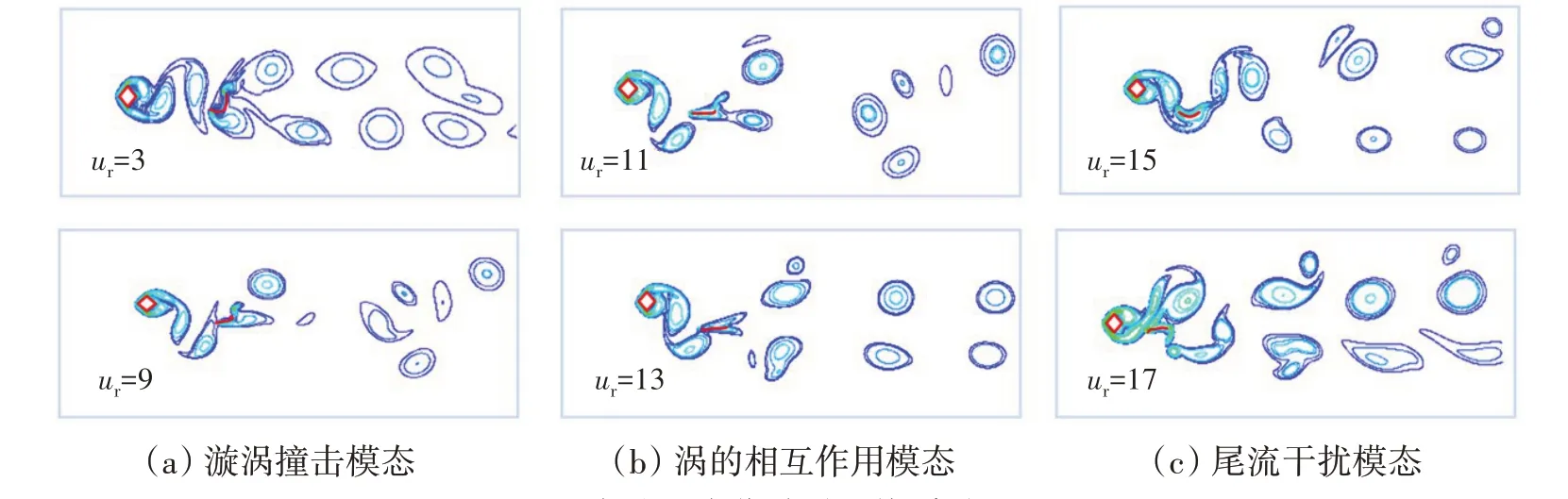
圖10 方柱最大位移時系統(tǒng)瞬時渦量圖Fig.10 Instantaneous vorticity graph of the system at the maximum displacement of the square cylinder

（1）旋渦撞擊模態(tài)。上游方柱上下剪切層交替卷起形成旋渦并向下移動，當與柔性梁主體發(fā)生碰撞時，撞擊使得下游柔性梁產(chǎn)生較大的脈動升力，使其自由端產(chǎn)生較大位移；與此同時，上游方柱產(chǎn)生的旋渦被截斷，截斷后的部分子渦分別與柔性梁自身的尾渦發(fā)生合并，并以渦對形式向下脫落；

（2）渦的相互作用流態(tài)。此時上游產(chǎn)生的旋渦不再撞擊下游柔性梁，而是與下游柔性梁下側產(chǎn)生的旋渦耦合產(chǎn)生相互作用，上游方柱受下游柔性梁的干擾較小，下游柔性梁振動則受到上游方柱渦脫的抑制；

（3）尾流干擾流態(tài)。此時，由于上游方柱順流位移較大，導致方柱與柔性梁間距較小，上游方柱上側剪切層再附到柔性梁表面，使得柔性梁完全沉浸在上游方柱的尾流中。

3.3 旋渦形成與脫落

圖11 展示了折減速度ur=9 時，在一個振動周期內(nèi)，方柱橫向振動位移Ay與柔性梁自由端橫向位移By的時程曲線及系統(tǒng)在點A、B、C、D的瞬時渦量圖，此時間距流態(tài)為漩渦撞擊模態(tài)，方柱與柔性梁自由端振動相位為反相位。在方柱的一個振動周期內(nèi)，方柱上側分離出一個渦在上行向后運動，下側分離出兩個渦，其中一個在下行向后運動并與柔性梁發(fā)生碰撞，另一個在上行向后運動，系統(tǒng)尾渦不規(guī)則。

圖11 ur=9時系統(tǒng)的振動響應Fig.11 Vibration response of the system at ur=9

圖12 展示了折減速度ur=13 時在一個振動周期內(nèi)系統(tǒng)的位移時程曲線及瞬時渦量圖，此時方柱與柔性梁自由端振動相位為同相位。此時方柱渦脫與ur=9類似，但系統(tǒng)尾渦呈‘2P’模式。

圖12 ur=13時系統(tǒng)的振動響應Fig.12 Vibration response of the system at ur=13

圖13 展示了折減速度ur=17 時，在一個振動周期內(nèi)系統(tǒng)的瞬時渦量圖，此時間距流態(tài)為尾流干擾模態(tài)，方柱處于振動鎖定區(qū)外。對于單方柱振動，在一個振動周期內(nèi)渦脫數(shù)量為偶數(shù)，且強度相等，方柱形成的XY軌跡也是對稱的‘8’字型軌跡。受下游柔性梁的影響，方柱每個振動周期內(nèi)有兩個旋渦脫落，旋渦在未完全脫離方柱時，便附著到柔性梁上，此時，上渦與下渦強度不一致，這也是導致柔性梁振動不對稱的主要原因。

圖13 ur=17時系統(tǒng)的振動響應Fig.13 Vibration response of the system at ur=17

4 結 論

本文基于IB-LBM方法提供了一套求解剛體-柔性體耦合系統(tǒng)流固耦合的計算方法。首先通過計算單方柱、單柔性梁的流致振動驗證程序在計算剛體-柔性體-流體耦合系統(tǒng)繞流問題時的可靠性。結果表明，本文提出的結合時間異步算法的多步直接力-格子Boltzmann 方法，能很好地處理剛體-柔性體-流體耦合系統(tǒng)的流固耦合問題。然后對低雷諾數(shù)（Re=100）下帶流向角α=45°方柱后附加柔性梁的流致振動進行了研究，發(fā)現(xiàn)帶柔性梁的方柱振動與單方柱振動具有顯著的區(qū)別，并得到如下結論：

（1）從計算結果上來看，柔性梁的模擬結果與已有文獻可以很好地吻合，表明了本文采用的方法可以很好地模擬柔性結構流固耦合問題;

（2）方柱下游附加梁的振動依然以橫流為主，隨著折減速度ur的增加，方柱均出現(xiàn)了明顯的振動鎖定區(qū)，對任意柔性梁長度，鎖定區(qū)域均大于單方柱情況下。在振動鎖定區(qū)域內(nèi)存在兩種振動狀態(tài)，當ur較小時，主要是平均升力系數(shù)不為零而導致的馳振，當ur較大時主要是由于振動頻率接近于固有頻率而導致的振幅較大；

（3）系統(tǒng)隨折減速度變化共出現(xiàn)了3種間距流態(tài)：尾流干擾、旋渦撞擊及渦的相互作用流態(tài)。

未來將對高雷諾數(shù)下帶流向角的方柱后附加柔性梁的流致振動進行模擬，并將結果與COMSOL軟件計算所得結果進行比較，做進一步驗證。