ASR 加并聯轉速微分負反饋的校正作用

曾新然

（廣東松山職業技術學院，廣東 韶關 512126）

一、引言

在電力拖動自動控制系統工程設計方法中，設計雙閉環直流調速系統時主要是根據生產機械和工藝所提出的靜態與動態性能指標要求［1］，將非典型系統通過選擇不同類型的調節器進行串聯校正成為典型系統。用該方法設計的雙閉環直流調速系統不僅結構簡單，工作可靠，設計和調試方便，更具有良好的動、靜態特性，在工業企業中是一種性能優良、應用廣泛的調速系統，目前在傳動領域中仍占有重要的地位［2］。

然而只采用PI 調節器串聯校正的方法有時還不能充分滿足系統動態性能指標的要求。在控制系統中各項指標之間往往存在著矛盾，要保證超調量不大，系統的快速性就會受到限制，而要有很強的抗擾能力，跟隨超調量就不會很小等等，只靠PI 調節器串聯校正難以兼顧。雙閉環調速系統一般均采用兩個PI 調節器，將電流環設計為典型Ⅰ型系統，速度環設計成典型Ⅱ型系統，系統在起動過程中轉速必須超調，才能使速度調節器退出飽和進入線性調節狀態，而且系統抗擾性能的提高也因此受到限制。當系統對轉速超調量和動態抗擾性能提出更高要求時，單憑PI 調節器進行串聯校正，難以實現，還需在原有轉速調節器的基礎上引入轉速微分負反饋環節對速度環進行并聯校正，利用微分負反饋的超前預判特性在轉速還未達到給定轉速前微分負反饋就起調節作用使速度調節器退出飽和，以此降低或消除超調量。

二、普通雙閉環直流調速系統

為了突出重點，不贅述工程設計、基本參數計算等內容，本研究選擇參數均已確定的普通雙閉環直流調速系統作為實例系統。側重點是速度環，以便后續在此基礎上引入速度微分負反饋后進行比較分析。

（一）系統動態結構框圖

1.電流環等效結構框圖

電流環的設計以跟隨性能為主，超調量小且穩態電流無靜差。因此ACR 采用PI 調節器將電流環串聯校正為典型Ⅰ型系統，取阻尼比=0.707，超調量為=4.3%。

電流環經簡化等效后成為轉速環中的一個環節，電流環的等效閉環傳遞函數和等效動態結構框圖如2-1 式和圖1 所示。

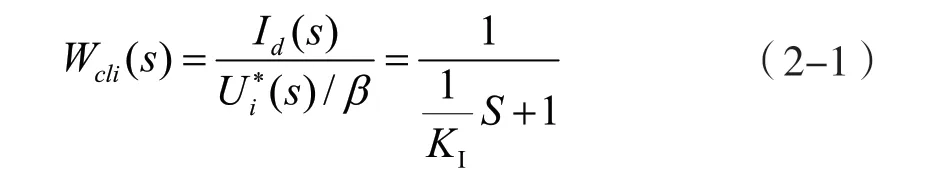
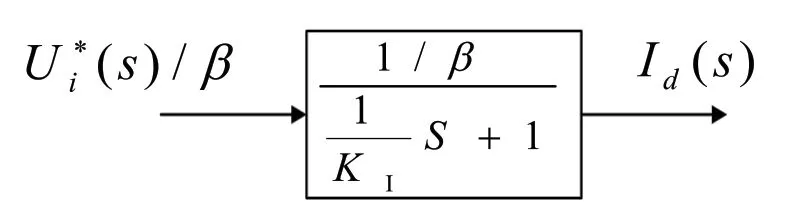
圖1 電流環等效動態結構框圖

2.速度環等效結構框圖

為了實現轉速無靜差且抗干擾能力強，ASR 采用PI 調節器將轉速環串聯校正成典型Ⅱ型系統，轉速環等效動態結構框如圖2 所示。

圖2 轉速環等效動態結構框圖

（二）線性超調與退飽和超調及計算

1.線性超調與退飽和超調的區別

在系統起動過程中，若速度調節器沒有飽和限幅約束，調速系統則可以在很大范圍內線性工作，在線性系統超調中只要中頻寬h 選定，無論穩態轉速高低，超調量都是固定值。當速度環按典型Ⅱ型系統設計時，取中頻寬h=5，超調量則為=37.6%［2］。

然而，實際系統在突加給定電壓后，轉速調節器很快就進入飽和狀態（達到限幅值）輸出恒定最大電壓，使電動機在恒流條件下起動，起動最大電流，轉速則按線性規律增長，起動過程要比速度調節器沒有限幅時慢得多，但限制了電動機起動的最大電流。轉速調節器一旦飽和，只有轉速超過給定轉速值（給定電壓值）轉速偏差電壓變成負值才能使速度調節器退出飽和狀態，之后只要電動機電流大于負載電流，電動機仍繼續加速，直到時，轉速開始降速，最后達到平衡狀態，速度穩定。因此在起動過程中轉速必然超調，但這已不是按線性系統規律的超調，而是經歷了飽和非線性區域之后的超調，稱之為退飽和超調。退飽和超調量與穩態轉速密切相關，穩態轉速越低超調量越大。根據文獻資料［2］可得計算公式2-2、2-3。

2.退飽和超調的計算

三、帶轉速微分負反饋的雙閉環直流調速系統

（一）微分環節及負反饋校正

1.微分環節

理想微分環節在階躍信號輸入作用下的輸出響應為一理想脈沖。由于微分環節能預示輸出信號的變化趨勢，當被調量還沒有變化，只是有了變化的趨勢時，其微分量就已經發揮作用，所以常用來改善控制系統的動態特性［3］，在系統中加人微分負反饋環節有助于抑制振蕩，減少超調量甚至消除轉速超調量。由于純微分容易引入干擾，在實際應用中常采用的是近似微分電路，如比例-微分電路。

比例-微分環節的傳遞函數：

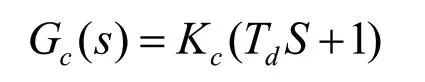
2.微分負反饋校正

微分負反饋校正在一般情況下屬于局部并聯校正，通過負反饋校正改變系統局部結構、參數，削弱非線性等因素的影響［4］，當系統控制質量要求較高時，采用這種局部反饋校正可以在串聯校正的基礎上進一步改善、提高系統動態性能。

（二）加入轉速微分負反饋的轉速環

1.帶轉速微分負反饋的速度調節器

通常反饋校正是在被調量的負反饋之外，再加被調量微分的負反饋。具體方法是在原有轉速調節器ASR（PI 調節器）基礎上，在速度反饋信號中再并聯微分電容和濾波電阻。

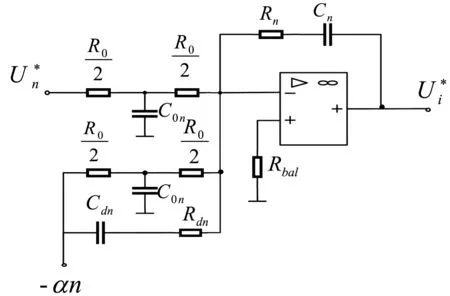
圖3 帶轉速微分負反饋的轉速調節器

由原理圖3 可得電流平衡方程式，整理后為3-1 式：

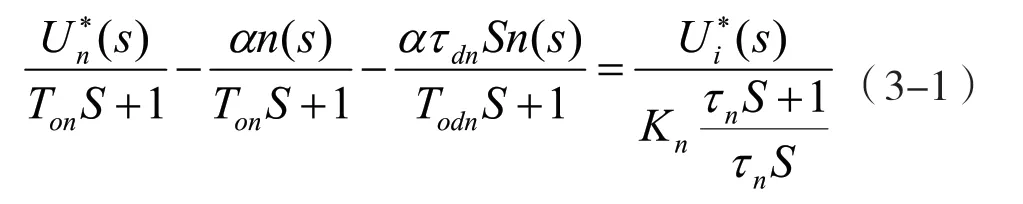
2.加入轉速微分負反饋的轉速環動態結構框圖

根據3-1 式并結合轉速環內的其他環節，可得到帶轉速微分負反饋的轉速環動態結構框圖4。

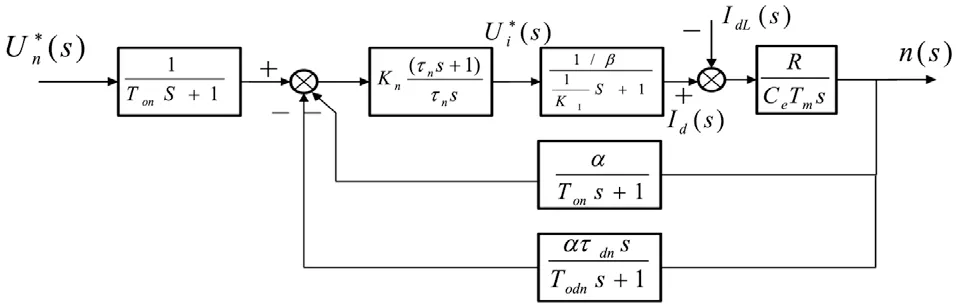
圖4 帶轉速微分負反饋的轉速環動態結構框圖

根據文獻資料［2］可得簡化后的結構框如圖5。

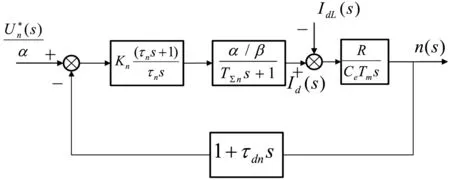
圖5 簡化后的結構框圖

帶轉速微分負反饋的轉速環動態結構圖簡化后，圖5 與普通雙閉環系統圖2 比較，只是在反饋通道中并聯了微分項，其作用是對系統進行并聯微分校正。

（三）系統加微分負反饋后退飽和時間和退飽和轉速

1.退飽和時間［2］

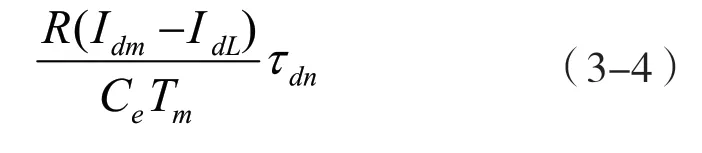
由于微分負反饋的作用，提前了退飽和時間，使系統未達到給定轉速時提前退出了飽和狀態，因此相應的超調量變小，甚至可以做到無超調。

3.轉速微分負反饋參數計算（實例系統轉速環按典型Ⅱ型系統設計）

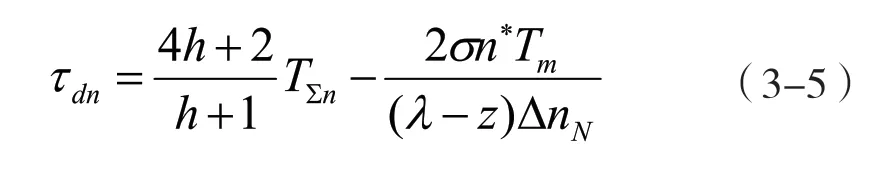
根據文獻資料［2］得無超調時的微分時間常數選擇為：

4.系統抗擾性能

帶轉速微分負反饋雙閉環直流調速系統的抗擾性能，因引入轉速微分負反饋后，動態速降大幅度降低，當中頻寬時：系統抗擾性能部分指標［2］如表1 所示。

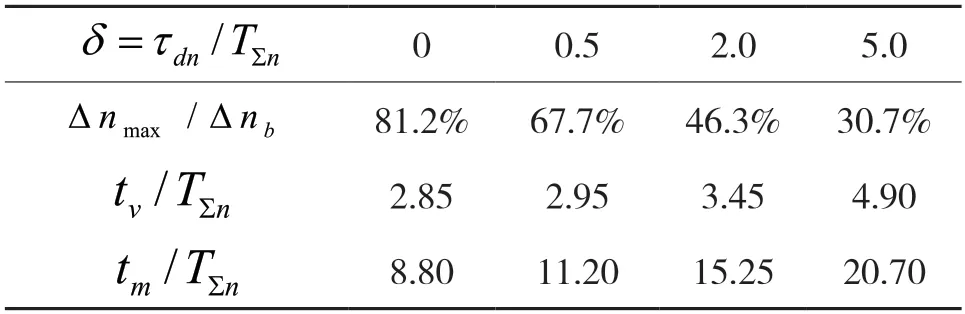
表1 抗擾性能指標

四、兩系統仿真及曲線比較

（一）帶限幅電路的ASR 調節器的 Simulink 仿真模型

該電路Simulink 仿真模型有三種形式：

1.PI 調節器的輸出端加一限幅環節；

2.積分輸出和調節器輸出各加一限幅環節；

3.積分帶限幅和PI 調節器輸出后加一限幅環節。

本文采用第3 種形式的Simulink 仿真模型，其特點是調節器的輸出等于其限幅值時，如果輸入信號改變極性，比例積分調節器是從積分本身的限幅值開始退去飽和，與控制系統實際電路的工作過程一致［5］，仿真結果與實際系統控制過程相符。

ASR 調節器傳遞函數：

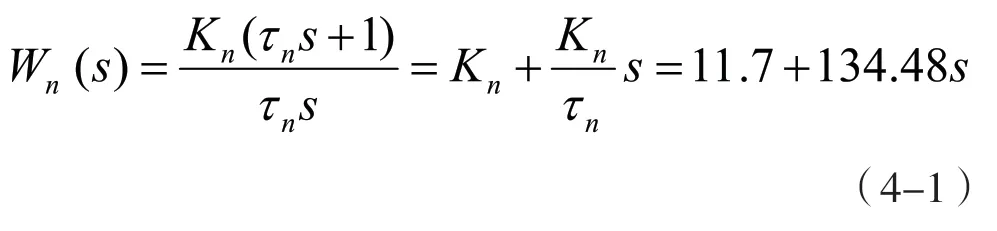
由4-1 式可得Simulink 仿真模型如圖6 所示。

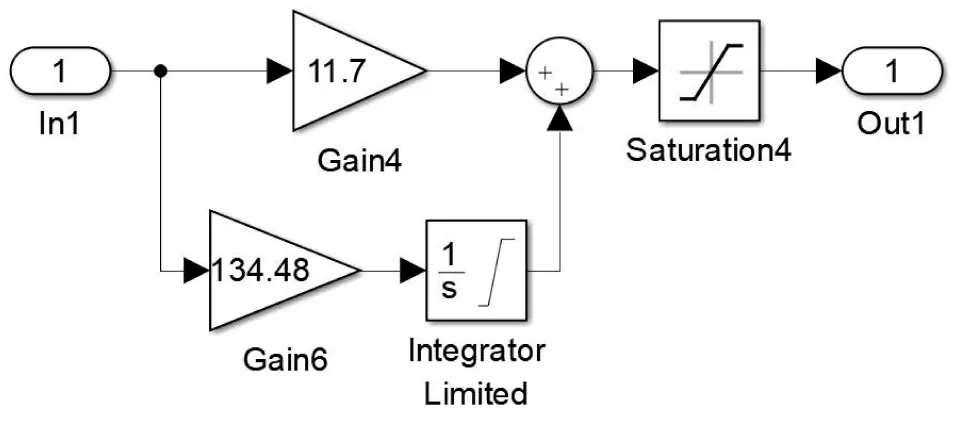
圖6 積分帶限幅和PI 調節器輸出加限幅的 Simulink仿真模型

（二）建立系統Simulink 仿真模型

1.實例普通雙閉環直流調速系統 Simulink 仿真模型如圖7 所示，仿真曲線如圖8 所示。

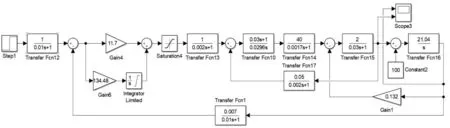
圖7 實例普通雙閉環直流調速系統 Simulink 仿真模型

2.帶轉速微分負反饋的雙閉環直流調速系統Simulink 仿真模型

帶轉速微分負反饋系統動態結構框圖與普通系統相比只是在原有速度負反饋環節上再并聯環節，如圖4 所示。帶轉速微分負反饋系統的速度負反饋等效環節傳遞函數為：

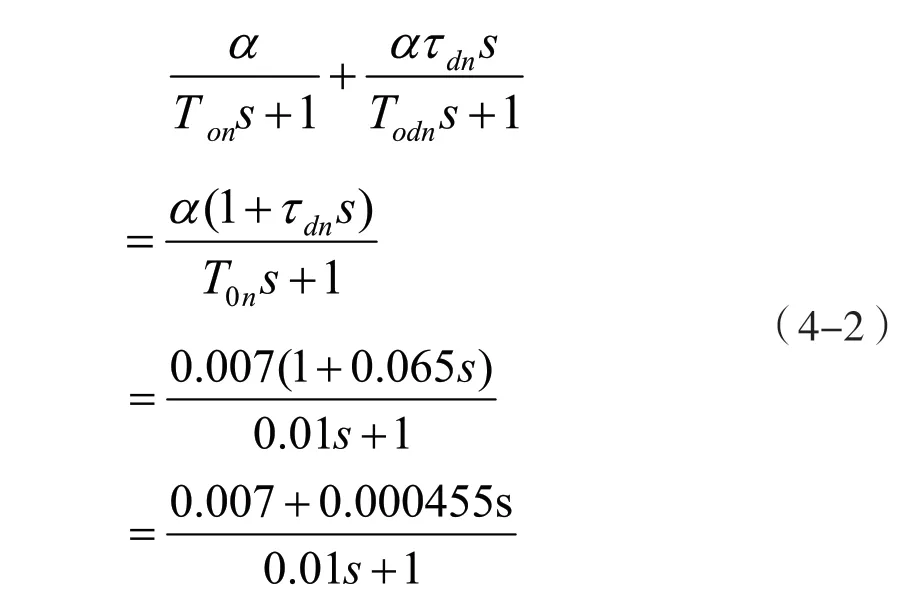
（三）兩系統仿真曲線比較分析

2.在圖8、圖10 中，曲線Ⅰ、Ⅲ為速度曲線，曲線Ⅱ、Ⅳ為電流曲線。圖中橫坐標為時間，單位為s，縱坐標為轉速、電流，單位分別為r/min、A，只有當電動機電流大于負載電流時，電動機轉速才開始上升，因此速度曲線不是從時間為0 開始發生動態變化的。系統最大電流限幅值為最大起動電流，ACR 輸出限幅10V，額定轉速ASR 輸出限幅10V。

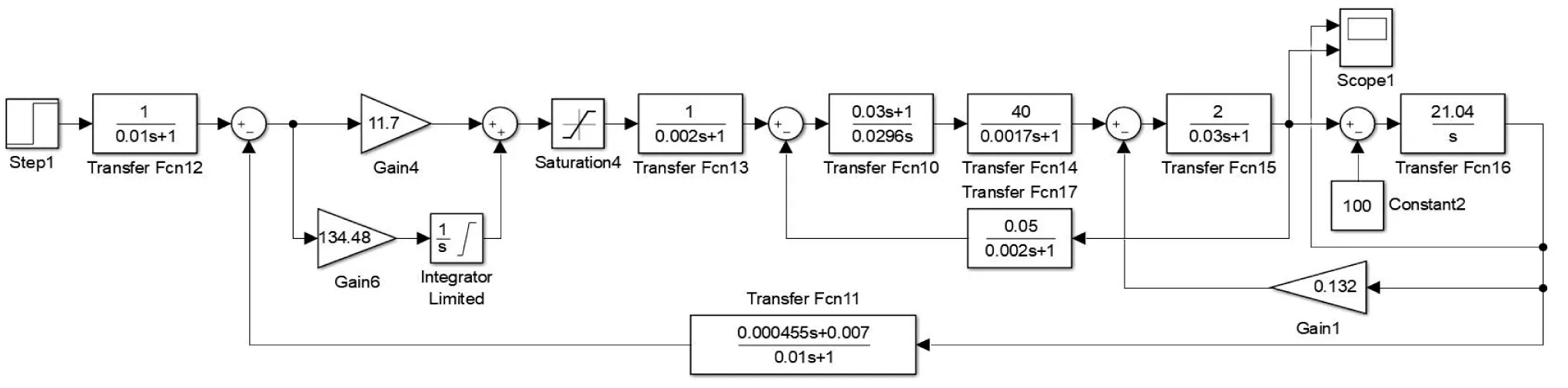
圖9 帶轉速微分負反饋的雙閉環調速系統 Simulink 仿真模型

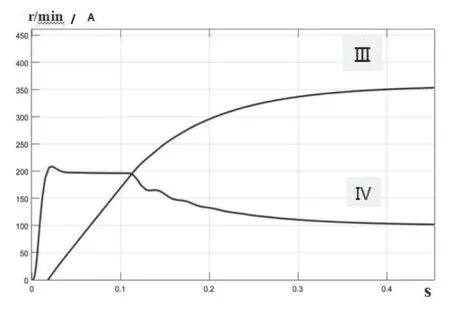
圖10 帶轉速微分負反饋系統仿真曲線

7.系統抗擾性能大大優于普通雙閉環直流調速系統，見表1 所示。通過系統仿真比較分析，系統采用轉速微分負反并聯饋校正后，在抑制（消除）超調，提高抗擾性能以及縮短最大起動電流時間等方面均收到了良好的效果。

五、結語

普通雙閉環直流調速系統要進一步降低超調量，甚至做到轉速無超調，只靠PI 調節器進行串聯校正是無法實現的。為此在原有速度調節器的基礎上，加入局部并聯速度微分負反饋對系統進行校正，利用微分環節能預示輸出信號的變化趨勢，當轉速還未超調，只是有了超調的變化趨勢時，其微分量就已經起著負反饋的調節作用，使系統提前退飽和的時間，在轉速還未到達給定轉速時速度調節器已退出飽和狀態，縮短了最大電流的起動時間，從而有效地抑制轉速超調量甚至做到無超調。

另一方面，加入轉速微分負反饋后系統動態速降大大降低，提高了系統動態抗擾性能。轉速微分負反饋時間常數越大，動態速降越小，但恢復時間將延長。當系統不允許出現超調時，應以無超調要求選擇參數，反之則須兼顧超調、動態速降和恢復時間進行全面綜合考慮來選擇參數。