基于STM32 的非線性失真放大器設計與測試分析

熊宇鵬，方如意，黃煜，陳炳權

（吉首大學信息科學與工程學院，湖南吉首 416000）

線性放大器輸入為正弦信號時，其非線性失真表現為輸出信號中包含各次諧波分量，常用總諧波失真(THD)衡量線性放大器的非線性失真水平[1]。在通信設備中，非線性元器件（晶體管、二極管）的非線性伏安特性會導致輸出的信號失真。計算信號的THD 值在通信設備的研發、生產和維護保障過程中有著重要的作用。

目前市面上的電子產品多種多樣，但是不論什么類型電子產品，都會產生噪聲，因此失真度測量儀的市場潛力很大。標準失真信號發生器是一種可用于失真度測試儀檢定的設備[2]。然而，我國對于失真度測量儀的研究起步較晚，目前市面上的失真度測量儀以國外進口為主，且價格相對較高。國內儀器大多采用旋鈕進行諧波的設置，參數調節不方便，使用效率低，步驟復雜，從而導致使用效率低。文中在對總諧波失真概念理解的基礎上，運用模擬電子技術知識搭建非線性失真放大器，測試驗證模塊以STM32 為控制核心，實現對信號的放大輸出與測量分析。

1 原理與設計

若信號放大100 倍，則需要有較大的增益，一般很難用單個三極管實現。若想實現穩定的增益，則需要引入負反饋，把增益轉換成兩個電阻的比值，而不是依靠單個晶體三極管的放大倍數。所以整個放大電路可以分為輸入-增益-輸出。放大器的非線性失真現象可以概述成4 種：頂部失真、底部失真、雙向失真、交越失真[3]。頂部失真是因為放大信號由直流信號與交流信號疊加，超過了三極管的線性區，線性區進入了飽和區導致直流偏置點錯誤，底部失真則相反。雙向失真則是因為在純交流信號的情況下，信號頂部與底部均增益過大。放大電路可以分為甲類、乙類、甲乙類，乙類與甲乙類放大電路是產生交越失真的原因[4]，乙類放大電路由兩個三極管組成，由兩個PN 結連接，若這兩個PN 結不導通，則會在過零部分產生畸變導致信號產生交越失真。從各類失真信號產生的原因來看，信號的放大需要有正確的偏置點，以適合增益大小。

1.1 非線性失真信號發生與放大器設計

非線性失真放大器裝置的第一部分是非線性失真信號發生與放大器。其第一、二級是放大倍數約為100 倍的阻容耦合多級共射放大電路，第三級是OCL 電路，通過模擬開關控制特定電阻電容是否接入OCL 電路，起到改變電路靜態工作點的作用，從而產生4 種非線性失真信號。輸入端為20 mV 的正弦波[5]，輸出端產生4 種非線性失真信號或無失真信號。可以使用示波器在輸出端口觀察產生的各種非線性失真信號波形。非線性失真信號發生與放大器設計框圖如圖1 所示。

圖1 非線性失真信號發生與放大器設計框圖

1.2 晶體管放大器電路論證與選擇

方案一：直接耦合的多級共射放大電路[6]。

優點：頻率范圍寬，放大倍數可調。

缺點：級間互相影響，靜態工作點難以調試。

方案二：阻容耦合多級共射放大電路[6]。

優點：各級獨立，靜態工作點無影響，容易調試成功，放大倍數可以通過加負反饋進行調解；

缺點：對低頻信號放大倍數不足。

由于測試信號為1 kHz 的中頻，在兩種放大電路的增益相差不多的情況下，選擇方案二更加有利于元件參數的確定以及靜態工作點的選擇，因此選擇方案二。

1.3 改變電路參數產生失真波形的輸出方案

方案一：在一二級共射電路中實現。

優點：比較容易產生頂部失真、底部失真。

缺點：放大電路的放大倍數不夠大，且增益不穩定[7]。

方案二：在第三級OCL 電路中實現。

優點：對前級電路放大倍數沒有影響，比較容易生成4 種非線性失真信號。

放大信號的重要指標包含增益與穩定度，雖然方案一中，頂部和底部兩種非線性失真信號容易實現，但是增益難以大于100，穩定度也不高。方案二選擇在第三級OCL 電路中輸出4 種非線性失真信號，與前級相對獨立，整個電路的放大倍數穩定，增益大于100，故選擇方案二[8]。

1.4 控制模塊的方案選擇

確定放大電路設計的方案后，需要對控制與測量分析模塊方案進行論證，這對計算總諧波失真度很重要。

方案一：增強型80C51 內核的STC 系列單片機可以達到的最高主頻為30 MHz，字長為8 位，具有ADC、PWM 等功能引腳和定時器及RCC 等內部資源，flash 一般比較小，操作簡單，運算速度略有不足[9]。

方案二：STM32 小系統板可以達到最高主頻為72 MHz，字長為32 位，具有ADC、PWM、DAC 等功能的引腳和TIM、RCC、DMA 等內部資源，flash 一般比較大，但是直接操作寄存器復雜，網絡資源比較豐富，可以嵌入emwin，支持觸摸屏，增強了與用戶之間的交互性。

STC 系列單片機成本雖然很低，但是無法滿足設計需求，STM32 擁有足夠的算力，而且有豐富的庫函數資源可利用，利于256-FFT 算法的編寫，因此選擇方案二。

1.5 非線性失真信號發生與放大器第一、二級的設計

第一、二級放大電路采用阻容耦合方式，兩級放大電路之間的直流通路各不相通，靜態工作點相互獨立，在理論計算和調試時可以單級處理。靜態工作點的計算式為：

式中，VCC的值為+12 V，Ie、Ib、IC分別代表發射級、基級和集電級的電流。放大電路的第一、二級原理圖如圖2 所示，其中第一級放大電路的發射極電阻Re=R8=800 Ω，基極回路電阻Rb=R1+R5=1 200 kΩ，集電極電阻RC=R2=3.3 kΩ，第二級放大電路Re=R28，Rb=R21+R25，RC=R22。

圖2 第一，二級電路設計原理圖

在Multisim12.0 軟件中，仿真得到第一級放大倍數β1約為20，第二級放大倍數β2約為6。第一、二級總的放大倍數大于100。

1.6 線性失真信號發生與放大器第三級OCL 電路設計

OCL 電路主要由NPN 和PNP 管組成，兩管參數對稱，接成射極輸出器[10]。第三級放大電路OCL 電路設計如圖3 所示，文中采用s8050(Q3) 為PNP 管，s8550(Q5)為NPN 管。當輸入信號為不等于0 時，在輸入信號周期內，兩管交替導通，即當輸入信號在正半周時，Q5發射結正偏導通，Q3截止輸出輸出信號的正半周。當輸入信號在負半周時，Q3發射結正偏導通，Q5截止，輸出輸出信號的正半周。兩管互補，各自導通半個周期，可以通過程序控制模擬開關的開關狀態改變Q5的工作狀態，輸出各種失真波形，從而輸出4 種非線性失真信號。

圖3 OCL電路設計原理圖

1.7 非線性失真信號發生與放大器整體電路設計

利用Multisim12.0 仿真平臺，在確定兩級放大電路與OCL 電路中各參數的值之后，進行PCB 板的制作，第一級放大電路的輸入接信號源、第二級放大電路的輸出接入OCL 電路的輸入信號端口、OCL 電路輸出接示波器進行波形的觀察研究[11]。整個非線性失真信號發生與放大器的原理圖如圖4 所示。

圖4 非線性失真信號發生與放大器原理圖

1.8 總諧波失真度的計算測量

非線性失真放大器裝置的第二部分是基于STM32 的總諧波失真度測量儀。該部分采用采樣率為10 240 Hz 的12 位ADC 模式對非線性失真信號發生與放大器輸出端的信號采樣，每次采樣256 次得到信號幅值為Ai,i=1,2,3,…,256。定義32 位long 類型變量Ii，高16 位存儲實部，即Ai變量，低16 位儲存虛部，方便FFT 計算。

調用DSP 庫函數，實現n=256 點FFT 計算，得到變量值Oi，它是一個包含相位信息的復數值，由此值計算得到該點的幅值Mi[12]。如式（2）所示，ri為變量Ii經過FFT 變換之后所得到值的實部，mi為變量Ii經過FFT 變換之后所得到值的虛部。

由于設定的采樣率fs=10 240 Hz,得出每點對應得頻率值fi為：

代入式（3）計算分辨率值為40 Hz,則每點對應的頻率值為0,…,1 000,…,2 000,…,3 000,…,4 000,…,5 000,…,5 120。則在程序中1 kHz、2 kHz、3 kHz、4 kHz、5 kHz 對應的索引分別為25、50、75、100、125，則：

其中，U1、U2、U3、U4、U5分別代表基波、二次諧波、三次諧波、四次諧波、五次諧波的幅值。根據總諧波失真的定義式可以計算得到THD值[13]：

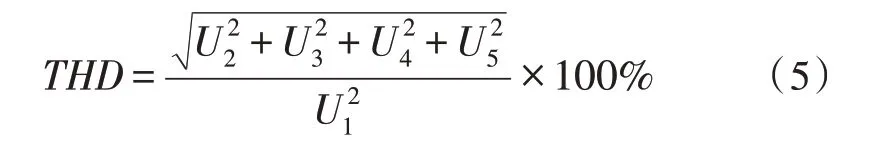
2 實 驗

2.1 Matlab 仿真測試

1）在Intel i5-7200U CPU@2.50 GHz 平臺上使用Matlab R2018a 軟件對1 kHz 的各種失真信號進行FFT 變換。仿真結果如圖5 所示。

圖5 Matlab 仿真結果中四種非線性失真信號波形

通過對比圖5(b)、圖5(d)、圖5(f)、圖5(h)可得出，頂部失真與底部失真的頻譜圖相同，因此這兩類波形的THD值也相同。觀察交越失真的頻譜圖可以發現，其三次諧波與五次諧波的幅值均大于其他非線性失真信號的三次諧波與五次諧波的幅值，因此其THD值最大。通過式（5）計算4 種非線性失真信號和無失真信號的THD值分別為19.306 6%，19.306 6%，23.078 0%，40.022 4%。由結果可以看出，當輸入信號幅值相同，經過相同增益的放大電路之后，頂部失真與底部失真的THD值相等。輸出信號的失真表現越明顯，則THD值越大[14]。

2）1 kHz 的對稱方波與對稱三角波的波形是偶對稱的，在傅里葉級數展開式中，除基波外，只有奇次項諧波無偶次項諧波，并且對稱方波的三次諧波、五次諧波的幅值分別為基波幅值的1/3、1/5，對稱三角波的三次諧波、五次諧波的幅值分別為基波幅值的1/9、1/25。1 kHz 對稱方波與三角波的理論THD值見表1，文中可以通過對稱方波與三角波來驗證非線性失真放大器測量所得THD值的準確性。

對稱方波的傅里葉級數展開式為[15]：

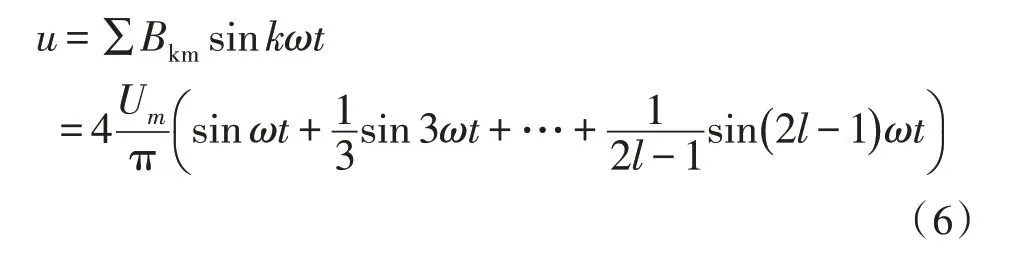
由式（5）與式（6）可以計算得出方波THD的理論值為38.873%。

對稱三角波的傅里葉級數展開式為[15]：

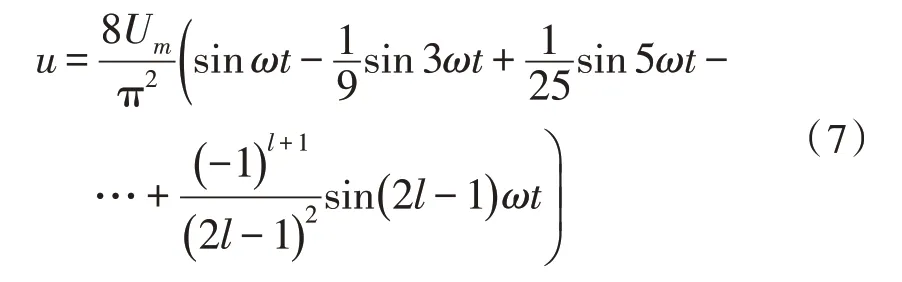
由式（5）與式（7）可以計算得出三角波THD的理論值是11.809%。

在Intel i5-7200U CPU @2.50 GHz 平臺使用Matlab R2018a 對1 kHz 的對稱方波與三角波進行仿真，得到的THD 值如表1 所示。

表1 對稱方波與三角波THD對比值

經過理論值與仿真值的對比可以發現，文中設計的非線性失真放大器計算得到的THD值與理論值只相差0.01%，精確到小數點后三位，可以認為此非線性失真放大器的THD測量值準確度高。

2.2 硬件電路測試結果

根據原理圖制作出PCB 電路板，輸入接信號發生器，接入頻率為1 k Hz、峰峰值為20 mV 的正弦信號，輸出接示波器，觀察在不同電路參數情況下產生的信號波形與幅值。4 種非線性失真信號波形的實際測試結果如圖6 所示。

圖6 實際測試結果中4種非線性失真信號波形

通過示波器觀察，輸出波形特征明顯，輸出幅度均大于2 V，與輸入信號20 mV 之比大于100，滿足設計需求[16]，4 種非線性失真信號波形的實際測試結果如表2 所示。

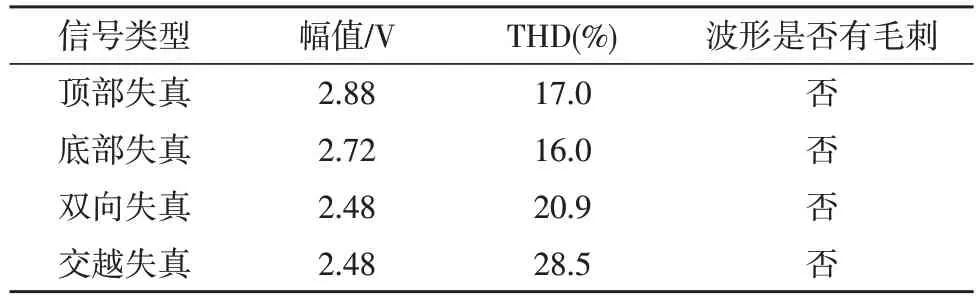
表2 各波形測試結果(測試數據)

根據實際測試結果，總結出4 種非線性失真信號的輸出波形增益均大于100，且輸出波形無毛刺。對比4 種非線性失真信號波形的THD值，可以總結出當波形無失真時，輸出波形的THD值接近于0，在相同放大倍數的情況下，頂部失真與底部失真的輸出波形THD值近似相等，交越失真由于其失真表現最明顯，因此其THD值最大。

需注意，Matlab 仿真中4 種非線性失真信號波形的失真表現與實際測試的失真表現不相同，所以測得的THD值不同。

3 結論

文中在基于模擬電子技術知識基礎上詳細介紹了非線性失真放大器的研究設計。首先，介紹了電阻電容等器件參數對放大電路的影響[17]，接著從這些影響因素出發，進行Matlab 仿真，觀察得到輸入信號通過放大電路之后，不同的電路參數對應不同的輸出波形，最終制作出實物作品。文中進行的非線性失真放大器的設計，通過從信號放大之后如何失真的角度進行研究，給優化非線性失真放大器裝置提供了理論依據。同時，文中介紹的非線性失真信號波形的總諧波失真度測量方法測試過程簡單，測試結果準確度高。