藥型罩間距對MEFP侵徹特征的影響研究

左亞帥，張會鎖，王家祺，李強，焦軍虎

(1.中北大學 機電工程學院，山西 太原 030051；2.山西中通高技術有限責任公司，山西 太原 030600)

爆炸成型彈丸(EFP)技術是聚能破甲技術的重要分支，EFP頭部質量集中，速度梯度小，開口半徑大，具有對炸高不敏感、能有效對付復合裝甲、后效作用良好等優點[1]。經過長時間的試驗和理論研究，EFP已經具有較為成熟和完善的理論[2-4]。多彈頭爆炸成型彈丸(MEFP)戰斗部相比于單枚EFP增加了毀傷元數量，不僅一次可生成多個彈丸，且每個彈丸可以具有不同的飛行方向，提高毀傷效率的同時還提高了命中精度，國內外都加大了對MEFP的研究[5-7]。

常見的MEFP戰斗部通常為軸對稱結構，將數枚藥型罩布于裝藥的端面或軸向[8]，以及通過在藥型罩前面布置不同形狀的柵格，利用網柵切割形成不同數量形狀的MEFP[9]。筆者主要針對端面分布式MEFP進行研究。目前對于MEFP的研究，主要集中在MEFP的成型過程，對于侵徹過程的研究較少[10-11]。由于彈頭侵徹靶板時靶板內多個應力波相互干擾作用及靶板各處形變不均，MEFP裝藥結構所形成的彈丸的侵徹效果會受到影響，將直接影響到MEFP的侵徹深度和毀傷面積。因此為了使MEFP的侵徹深度可以得到控制，筆者采用數值模擬計算，分析相鄰藥型罩間距對MEFP侵徹深度的影響，對于MEFP設計具有重要的參考價值。

1 數值模型

1.1 裝藥結構及材料參數

選用φ60 mm球缺型變壁厚藥型罩EFP戰斗部，裝藥結構長徑比N=1；藥型罩采用紫銅材料，罩頂厚δ=2.1 mm、外曲率半徑r1=54 mm、內曲率半徑r2=58 mm。采用中心點起爆方式引爆JH-2炸藥。單枚球缺型EFP裝藥結構如圖1所示。

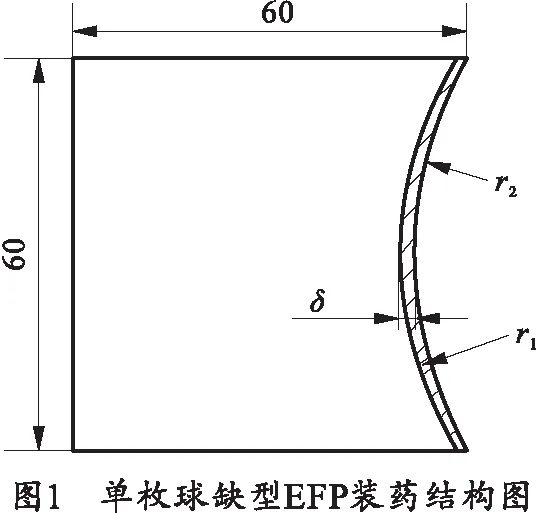
使用Autodyn進行數值模擬，聚能裝藥爆炸、藥型罩翻轉成型、EFP侵徹靶板等過程是多物質相互作用的過程，因此采用拉格朗日算法進行計算。拉格朗日算法是解決爆炸與沖擊問題應用中最為廣泛的一種方法，每個單元的頂點隨填充材料一起移動，由于網格與材料一起變形，填充材料始終保持在原單元內而不會在單元之間流動[12]，拉格朗日算法中很容易確定材料和結構界面以及內部應力應變狀態，可以很好地模擬固體材料的動態行為[13]。模型中藥型罩使用紫銅，靶板使用4340鋼，炸藥使用JH-2，各部分材料的狀態方程、強度模型及失效模型如表1所示。其中紫銅和4340鋼參數在Autodyn材料庫中選取，JH-2炸藥JWL狀態方程參數如表2所示。

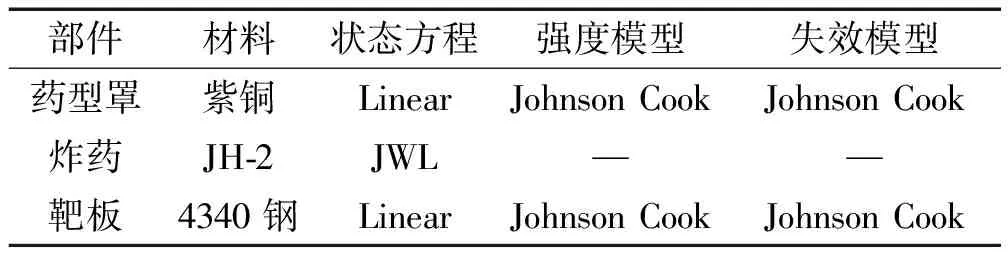
表1 材料模型

表2 JH-2炸藥JWL狀態方程參數

1.2 單枚EFP數值仿真模型的驗證

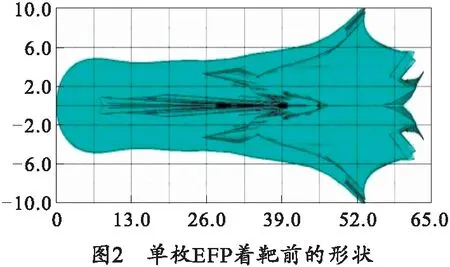
使用圖1所示EFP裝藥彈丸結構侵徹靶板，靶板為半無限鋼靶，文獻[14]中所述有利炸高為3.9～4.4倍裝藥直徑，筆者采用直徑為60 mm的裝藥結構，因此取炸高為240 mm，網格寬度為0.5 mm，總網格數約為350 000。圖2所示為EFP到達靶板前時的形狀，彈丸頭部速度為2 598 m/s，采用定常流體模型對侵徹深度進行簡便計算[15]：

(1)

式中：P為侵徹深度；l0為EFP的有效長度；η為EFP密實度；ρp和ρt分別為彈丸和靶板的密度。取l0為53 mm，EFP密實度η為0.85，彈丸密度ρp為8.96 g/cm3，靶板密度ρt為7.83 g/cm3，理論計算侵徹深度為52.27 mm。

數值模擬侵徹結果如圖3所示，彈孔直徑約為61.54 mm，侵徹深度為52.18 mm，與理論計算值吻合，且仿真結果形貌與文獻[14]試驗靶板剖面相吻合，證明用上文所述算法、材料模型及網格數量進行仿真所得結果是合理的。

2 藥型罩間距影響分析

2.1 MEFP侵徹鋼板過程分析

MEFP裝藥結構如圖4所示，圖中D為藥型罩直徑，d為藥型罩間距，由于對MEFP整體結構進行仿真所需計算資源過大，因此將模型簡化，對MEFP相鄰兩子裝藥進行仿真，能在一定程度上反映MEFP整彈的侵徹情況。

取藥型罩外壁之間最短距離d=10 mm，不同時刻的侵徹過程及結果如圖5所示，侵徹深度P隨時間t變化曲線如圖6所示，MEFP侵徹鋼板過程如下：

1)從子彈丸接觸靶板開始計時，5 μs前靶板中應力主要集中在彈頭與靶板接觸的沖擊界面上，至10 μs時形成比彈徑略大的彈坑。此階段屬于開坑階段。

2)從10 μs至40 μs，應力波開始相互作用，最大應力出現在應力波交互作用區域中部，隨時間增加，應力逐漸向靶板內傳遞。彈丸侵徹速度穩定，沖擊界面附近的靶板介質在受到沖擊之前，已經獲得了一定的軸向和徑向速度，在徑向飛散的彈丸進一步作用下，彈孔直徑擴大，侵徹深度增加[16]。此階段屬于侵徹的穩定階段。

3)40 μs開始，應力分布基本穩定，應力變化主要集中于彈坑底部及兩彈孔的中間區域，此時彈丸速度已經降為767 m/s左右，且速度下降很快，靶板的強度作用表現越來越明顯，侵徹能力變弱，侵徹深度增加較小。由于靶板內應力波的相互作用及兩彈丸中間部分靶板形變大于靶板其他位置，使得彈孔向中間傾斜。兩彈孔中間的靶板強度變弱，破碎彈丸的侵蝕作用表現明顯，兩彈孔中間的靶板強度被進一步削弱，加大了彈孔底部的傾斜程度。

4)80 μs后，彈丸基本失去侵徹能力，彈丸在彈孔底部徑向速度明顯大于軸向速度，主要表現為擴孔作用，此階段屬于侵徹的終止階段。

2.2 藥型罩間距對孔徑和傾斜程度的影響

炸高取240 mm，研究不同藥型罩間距對MEFP侵徹鋼靶彈孔形狀的影響，如圖7所示，隨藥型罩間距增加，彈孔形狀發生較大改變，最明顯的為彈孔傾斜程度和彈孔直徑的改變。

以兩彈丸著靶點連線的中點為原點，建立坐標系，如圖8所示，X軸與彈孔輪廓交于點A、B，作平行于X軸的直線過彈孔輪廓上X最大值點D，與另一側輪廓交于點C，取直線AB中點E和直線CD中點F，直線EF與Y軸夾角θ即為彈孔傾斜角度，AB的距離即為彈孔直徑φ。

以兩彈丸著靶點連線的中點為原點，不同藥型罩間距下彈孔輪廓如圖9所示，隨藥型罩間距的增加，彈丸間相互作用減弱，靶板內沖擊波交互作用時間延后，兩彈中間靶板形變程度與其他部位靶板形變程度逐漸接近，彈孔傾斜角度逐漸變小，彈孔直徑有所增加；當藥型罩間距等于藥型罩直徑時，彈孔傾斜角度約為3.8°，彈孔直徑約為單枚EFP彈孔直徑的93.3%，具體數據如表3所示，表中d為相鄰藥型罩外壁最小間距，D為藥型罩直徑，θ為彈孔傾斜角度，φ為彈孔直徑。

表3 彈孔傾斜角度與彈孔直徑

藥型罩間距與彈孔傾斜角度及彈孔直徑之間的關系如圖10所示。

藥型罩間距與彈孔傾斜程度和彈孔直徑之間呈現明顯的正相關，說明隨藥型罩間距的增大，彈孔傾斜角度變小，彈丸具有更多的剩余能量用于擴孔。當藥型罩間距大于1.2倍單枚彈徑后，彈孔基本不傾斜，孔徑增加變緩。

2.3 藥型罩間距對侵徹深度的影響

如圖11所示，以兩彈著靶點連線的中點為坐標原點，建立坐標系，X軸與彈孔輪廓交于點A、B，作平行于AB的直線，與彈孔底部相切于點G，該直線與X軸的距離即為垂直侵徹深度P1，作平行于彈孔中心線的直線，過點G與直線AB交于點K,KG之間的距離即為最大侵徹深度P2，因此，最大侵徹深度與垂直侵徹深度之間的關系為

P2=P1cosθ.

(2)

兩彈丸時，垂直侵徹深度具體數據如表4所示，最大侵徹深度具體數據如表5所示。

表4 兩彈丸垂直侵徹深度

表5 兩彈丸最大侵徹深度

藥型罩間距d大于藥型罩直徑D后，侵徹深度增加變緩，最大侵徹深度和彈孔形狀與單枚EFP侵徹效果接近。

藥型罩間距與侵徹深度之間的關系如圖12所示，其中局部放大圖為藥型罩間距小于單枚彈徑時侵徹深度散點圖，發現當藥型罩間距小于單枚彈徑時，藥型罩間距與侵徹深度表現為明顯正相關的線性關系。

對垂直侵徹深度12個散點進行線性擬合，自由度為10。采用y=a+bx進行擬合，其中y=P1/D，x=d/D，當a=0.803 49時標準差為3.735 48×10-4，當b=0.033 61時標準差為7.989 5×10-4，經過整理得到垂直侵徹深度P1為

P1=0.803 5D+0.033 61d.

(3)

對最大侵徹深度6個散點進行線性擬合，自由度為4。采用y=a+bx進行擬合，其中y=P2/D，x=d/D，當a=0.808 15時標準差為3.909×10-4；當b=0.031 4時標準差為7.583×10-4，經過整理得到最大侵徹P2為

P2=0.808 2D+0.031 4d.

(4)

式(3)和式(4)所擬合直線的殘差平方和分別為7.878×10-6和1.640 3×10-6，殘差平方和越小表明擬合程度越好。Pearson相關系數分別為0.997 2和0.998 8，表明藥型罩間距與侵徹深度之間表現為極強正相關。可決系數R2分別為0.993 8和0.997 1，表明擬合優度好，回歸直線對觀測值的擬合程度高，因此，所擬合直線能夠準確反映藥型罩間距和侵徹深度之間的關系。

綜上所述，隨藥型罩間距的增加，侵徹深度逐漸增加，最大侵徹深度相較于垂直侵徹深度，雖增長速度有所減緩，但差別不大；并且隨藥型罩間距增加，侵徹所形成的彈孔傾斜程度逐漸減小，彈孔直徑逐漸增加。說明當藥型罩間距過小時，彈丸能量主要消耗在彈丸之間的相互作用，及彈丸對兩彈中部靶板的橫向侵徹和擠壓。當藥型罩間距d大于藥型罩直徑D后，彈丸之間的相互影響基本可以忽略不計，且兩彈中間靶板形變程度與其他部位靶板形變程度逐漸持平，MEFP的最大侵徹深度達到單枚EFP侵徹深度的96.6%，認為藥型罩間距大于藥型罩直徑后，侵徹深度受到的影響迅速減少。

3 結論

1)對MEFP進行數值模擬，發現侵徹后所形成的彈孔向中間傾斜。隨藥型罩間距的增加，傾斜角度逐漸減小，彈孔直徑逐漸增大；當藥型罩間距等于藥型罩直徑時，彈孔基本不發生傾斜，傾斜角度約為3.8°。當藥型罩間距大于1.2倍藥型罩直徑后，彈孔傾斜程度和孔徑所受到的影響迅速減小。

2)對兩彈丸侵徹過程進行分析，發現隨藥型罩間距增加，最大侵徹深度逐漸增加，由0.81倍彈徑增加至0.858倍彈徑；同時彈孔傾斜程度減少，傾斜角度由6°逐漸垂直；彈孔直徑逐漸增加，由0.9倍彈徑上升為0.99倍彈徑；說明藥型罩間距過小時，部分能量消耗與彈丸間的相互作用及對彈孔底部的徑向侵蝕，這部分能量大于開孔所需能量。

3)當藥型罩間距大于彈徑后，MEFP最大侵徹深度達到單枚EFP侵徹深度的96.6%，隨藥型罩間距進一步增加，MEFP最大侵徹深度逐漸與單枚EFP侵徹深度接近，彈孔形狀與單枚EFP相吻合；藥型罩間距小于彈徑時，藥型罩間距與侵徹深度之間表現為明顯的正相關線性關系。因此對于MEFP設計來說，在幾何尺寸條件允許的情況下，應盡可能加大藥型罩間距，減少能量消耗和彈丸間相互作用，在提高侵徹深度的同時，增大毀傷面積，本研究對于MEFP戰斗部研制具有一定的參考價值。