脆性材料機械加工表面粗糙度模型的研究進展

馬廉潔 李紅雙

1.東北大學機械工程與自動化學院，沈陽，1108192.東北大學秦皇島分校控制工程學院，秦皇島，066004

0 引言

已加工表面質量(表面完整性)對機器零件的使用性能(耐腐蝕性、耐磨性和疲勞強度等)具有重要影響[1]，包含表面幾何學和表面層材質的變化兩方面的內容。表面層材質的變化有多種形式表達，如殘余應力、硬度變化、電磁特性變化等。表面粗糙度是表面幾何學的表征，是用來鑒別工件表面質量好壞的重要指標之一。合理控制表面粗糙度是提高零件性能、延長使用壽命的手段之一。工件表面形成過程受加工系統眾多變量影響，而且這些變量的作用結果往往是非線性、相互依賴或難以量化的，因此常常依賴于一線人員的經驗，不可避免地造成生產浪費。因此，探究工件表面形成機理，建立表面粗糙度預測模型對控制加工表面質量、提高加工效率、優化工藝參數以及降低加工成本等具有重要意義。

陶瓷、硅晶體、光學玻璃等脆性材料因其抗腐蝕、抗磨損、耐高溫等優良性能被廣泛用于光伏發電、電子和航天航空等諸多領域，應用前景非常廣闊[2-4]。脆性材料的斷裂韌性一般較差，屬典型難加工材料，易產生裂紋、脆性凹坑等缺陷[5]。一般認為，脆性材料在加工過程中的材料去除方式有塑性剪切和脆性崩碎[6]，而金屬材料的材料去除方式只有塑性剪切去除[7]。因此，針對金屬材料建立的表面粗糙度模型對脆性材料不一定適用。

表面粗糙度的建模方法主要分為經驗參數建模方法和理論建模方法[8-9]。經驗參數建模方法不考慮材料去除機理，而是利用數據挖掘方法建立加工參數與表面粗糙度的數值關系。理論建模方法需要準確認識加工過程中的材料去除機理，并以此為依據來建立模型。

本文首先對表面粗糙度的表征參數進行簡要介紹，而后對經驗建模方法和理論模型進行了歸納分析，對各種粗糙度模型的發展歷程、重要的研究成果及其特點等進行了總結和討論，最后對表面粗糙度模型未來研究方向進行了展望。

1 表面粗糙度的表征參數

如圖1所示，在工件已加工三維表面上垂直截取一橫截面(二維表面廓形)，該橫截面上的表面廓形由取樣長度不同的波度和表面粗糙度組成。波度是加工表面周期性重復出現的幾何形狀誤差，是影響配合零件實際接觸面積的一種宏觀粗糙度，而表面粗糙度是加工表面的微觀幾何形狀誤差。

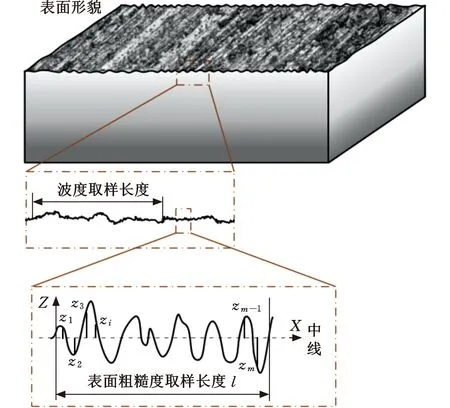
圖1 已加工工件三維表面形貌示意圖

目前有幾種不同的表面粗糙度參數定義評價表面廓形，如算術平均粗糙度Ra、峰-谷粗糙度Rt、微觀不平度十點平均高度Rz和中線平均偏距Sm等，其中，算術平均粗糙度Ra和峰-谷粗糙度Rt最為常用。

峰-谷粗糙度Rt為取樣長度l上，最高峰和最低谷的高度差，即

Rt=zmax-zmin

式中，zmax、zmin分別為取樣長度l上，輪廓最高峰和最低谷至中線的距離。

算術平均粗糙度Ra為取樣長度l上，表面廓形相對中線(將廓形分成上下面積相等兩部分的一條特定直線，如圖1所示)的平均偏離值，即

式中，zi為取樣長度l內第i個取樣點至中線的距離；m為在取樣長度l內輪廓高度的測量次數。

2 經驗參數建模方法

經驗參數建模方法利用各種數據挖掘方法(多元回歸、經驗公式、神經網絡、支持向量機等)建立加工參數與表面粗糙度之間的關系。

2.1 多元回歸方法

多元回歸方法首先建立加工參數和表面粗糙度之間的函數關系：

(1)

式中，β0為常數；n為試驗數據組數；βi為線性系數；xi、xj為加工參數；βii、βij為二次項系數；ε為實驗數據誤差。

隨后對大量實驗數據進行多元回歸分析，確定模型系數。

李春林等[10]采用慢刀伺服車削工藝對光學鏡片進行曲面加工，研究了刀具圓弧半徑、進給速度、背吃刀量、主軸轉速及離散角對表面質量的影響，建立了以粗糙度為響應的多元回歸數學模型。該模型分析了各因素對表面粗糙度的影響，發現刀具圓弧半徑影響最顯著，進給量和背吃刀量次之。ABDULKADIR等[11]利用多元回歸方法研究了前角、刀尖半徑和進給速度在超精密加工單硅晶片中對表面粗糙度的影響，研究結果表明：進給速度對粗糙度的影響最大；低速進給的表面質量更好。

采用多元回歸方法建立的模型簡單、計算速度快，但存在擬合系數大小不均一的問題，故出現了將多元回歸和其他方法相結合的改進型回歸方法。

2.2 經驗公式方法

經驗公式方法考慮加工過程中的非線性影響因素，建立加工參數與表面粗糙度之間的指數模型：

(2)

式中，c0為工件材料和切削條件決定的修正系數；yi為加工參數；ci為yi對應的指數；i為加工參數的數目，i>1。

磨削過程中，磨粒磨損和振動等因素導致理想表面粗糙度遠小于實際表面粗糙度。為提高模型精度，SNOEYS等[12]在運動學模型的基礎上提出了粗糙度經驗方程：

(3)

式中，vw為工件進給速度；vs為砂輪線速度；ap為磨削深度；R、x均為實驗確定的常數。

經過對數變換、量綱一化、增加二次修正項等手段，經驗公式的指數表達形式求解問題可轉化為二次多項式回歸問題。與直接采用的多元回歸方法相比，經驗公式的預測結果與試驗值的擬合精度更高。

WANG等[13]結合氧化鋯陶瓷磨削正交試驗，分析了磨削深度、砂輪速度和工件進給速度對表面粗糙度的影響，并根據實驗數據提出了氧化鋯磨削表面粗糙度經驗公式，與實驗值相比，模型預測值的最大相對誤差小于5%，具有較好的預測效果，模型可信程度高。王興盛等[14]采用正交試驗回歸分析法預測鏡片精密車削表面粗糙度，建立了考慮刀具圓弧半徑、每圈進給量、背吃刀量、主軸轉速和離散角度的粗糙度指數預測模型，試驗結果表明，模型的預測效果好，但模型訓練誤差較大。

2.3 神經網絡方法

人工神經網絡具有很強的非線性建模能力，廣泛用于預測表面粗糙度、切削力、切削溫度和刀具磨損[15-19]，但極易限于局部極值，且學習很慢，因此，一般需改進神經網絡結構或結合其他算法一起使用，以改善性能、提高收斂速度。

馬廉潔[20]通過CBN砂輪點磨削低膨脹微晶玻璃的單因素實驗研究了表面粗糙度與工件進給速度、砂輪線速度、磨削深度、砂輪傾斜角和偏轉角之間的關系，利用BP神經網絡進行單因素數值擬合；基于數值擬合結果，提出了點磨削低膨脹微晶玻璃表面粗糙度的多元復合模型；結合正交實驗及粒子群算法對模型進行了優化。該模型經檢驗能較好地反映加工參數對表面粗糙度的影響，具有一定的可信度。王曄[21]結合可加工陶瓷車削實驗數據，采用變異人工魚群算法優化的BP神經網絡(IAFSA-BP)，預測了單個加工參數(切削深度、進給速度和主軸轉速)與粗糙度的關系，實驗結果表明，預測結果可靠，且IAFSA-BP預測精度明顯優于BP。

神經網絡預測模型基于數據信號的采集及處理，故采集數據信號的準確性及處理手段都會影響模型的預測精度。模型精度依賴于訓練的樣本數據，當實驗數據在樣本范圍之內時，其預測值與實驗值之間誤差較小，反之，其預測值與實驗值誤差較大。

2.4 支持向量機方法

支持向量機(support vector machine，SVM)是一種以統計學習理論為基礎的機器學習方法，被推廣用于回歸分析、函數擬合等問題。SVM模型的網絡結構與神經網絡的網絡結構類似，都是從輸入到輸出的網絡映射。訓練樣本時，根據神經網絡方法建立模型的學習能力難以控制，容易產生過學習。SVM通過結構風險最小化控制了機器的學習能力，避免產生過學習，除此之外，SVM還具有泛化能力良好、學習快等優點。

ZHANG等[22]基于不同材質光學玻璃的磨削實驗、支持向量機理論，研究了砂輪粒度、磨削深度、砂輪轉速、工件進給速度、玻璃材質對光學元件表面質量的影響，建立了在線監測光學元件表面質量的模型。該模型包含識別模型和插值因子支持向量機，試驗證明該模型表面粗糙度的報警準確率為85.19%。孫林等[23]利用最小二乘支持向量機(LS-SVM)研究了磨削用量對表面粗糙度的影響，將砂輪速度、工件速度、磨削深度作為模型輸入，將表面粗糙度作為模型輸出，通過加工試驗對粗糙度模型預測精度進行了驗證。相較于多元線性回歸模型和神經網絡模型，LS-SVM模型具有較高的預測精度，并具有樣本外插能力強、操作方便等優點。

支持向量機與神經網絡類似，需要大量實驗獲取的較密集數據來支撐預測模型，以使預測結果更加精確。

經驗參數建模方法的建立依賴實驗樣本數據，經過大量樣本數據訓練后，模型精度才會不斷提高，但該方法過度依賴加工條件和設備，不具有普遍適用性。除此之外，經驗參數建模方法不考慮實際加工過程和材料去除機理等，缺乏對加工過程本質的描述。

3 粗糙度理論模型

加工過程中，由于切削刃與工件的相互作用，已加工表面會留下周期性條紋。最基礎的粗糙度理論模型只考慮切削刃與工件的干涉關系，因此該模型被稱為運動學模型。機理模型是在深入了解材料去除過程和表面形成機理的基礎上建立的，更符合實際加工過程。

3.1 粗糙度運動學模型

MALKIN等[24]基于磨削加工中的運動學分析，假設工件表面溝紋完全由磨粒切削刃作用產生(圖2)、磨粒出露高度相等且等間距均勻排布，首先建立了磨削運動學模型：

圖2 磨削縱向理論輪廓示意圖

(4)

式中，ds為砂輪直徑；L為磨粒間距。

由式(4)可以看出，粗糙度主要取決于速度比vw/vs和磨粒間距L，與磨削深度無關，且受砂輪直徑的影響較小。Malkin運動學模型的預測值僅為實驗值的1/1000，預測精度較低，且模型中的粗糙度與磨削深度無關。盡管Malkin運動學模型與加工實際存在較大偏差，但它最先對表面粗糙度進行定量表達，對磨削表面粗糙度的理論研究具有指導意義。

車削加工中，工件的已加工表面存在周期性溝槽，這在一定程度上反映了車刀與工件的干涉關系，如圖3所示。BOOTHOYD[25]考慮刀具-工件干涉關系，建立了車削運動學模型:

圖3 圓弧刀刃車削模型示意圖

(5)

式中，vf為車刀的進給速度；rε為刀具圓弧半徑。

該模型較為簡單，僅適用于圓弧刃刀具，且預測精度較低。

VAJPAYEE[26]根據粗糙度與刀具的幾何關系(圖4)，在式(5)的基礎上(切削刃與工件的干涉關系見圖4b)，進一步考慮不同刃口形狀及走刀痕跡的影響，分別建立了直線刃刀具粗糙度模型(式(6))和圓弧刃刀具粗糙度模型(式(7))：

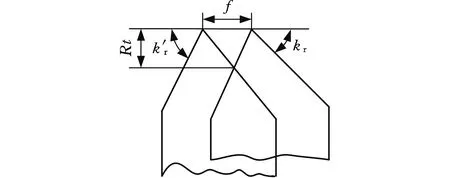
(a)直線刃刀具

(6)

式中，kr為刀具主偏角；k′r為刀具副偏角;f為車削進給量。

Rt=

(7)

Vajpayee建立的粗糙度模型僅取決于刀尖圓弧半徑、進給速度、主偏角和偏角等參數。模型形式簡單、誤差較大，僅考慮理想形貌下的車刀與工件的干涉關系。

粗糙度運動學模型是最先建立的粗糙度理論模型，模型形式簡單，僅考慮加工用量和切削刃幾何角度與粗糙度的關系，雖然模型誤差大，但對進一步完善粗糙度理論模型具有很好的借鑒意義。

3.2 機理模型

3.2.1臨界加工參數

近年來，諸多學者圍繞脆性材料脆塑轉變的臨界條件進行了大量研究。BIFANO等[27]根據Griffth裂紋擴展判定準則及單顆磨粒的壓痕實驗，基于能量優先假說(工件產生塑性變形還是脆性斷裂取決于其去除方式所需的能量是否先得到滿足)，建立了靜態條件下的臨界切削深度計算公式：

(8)

式中，dc為臨界切削深度；μ為由材料決定的常數；KIC為材料斷裂韌性；E1為材料彈性模量；H為材料顯微硬度。

Bifano臨界切削深度模型是應用顯微壓痕法建立起來的。圖5所示為單顆磨粒的壓痕模型[27]。實驗過程中，載荷緩慢施加，近似于靜態，材料斷裂韌性KIC是靜態值，這與實際加工過程并不相符。

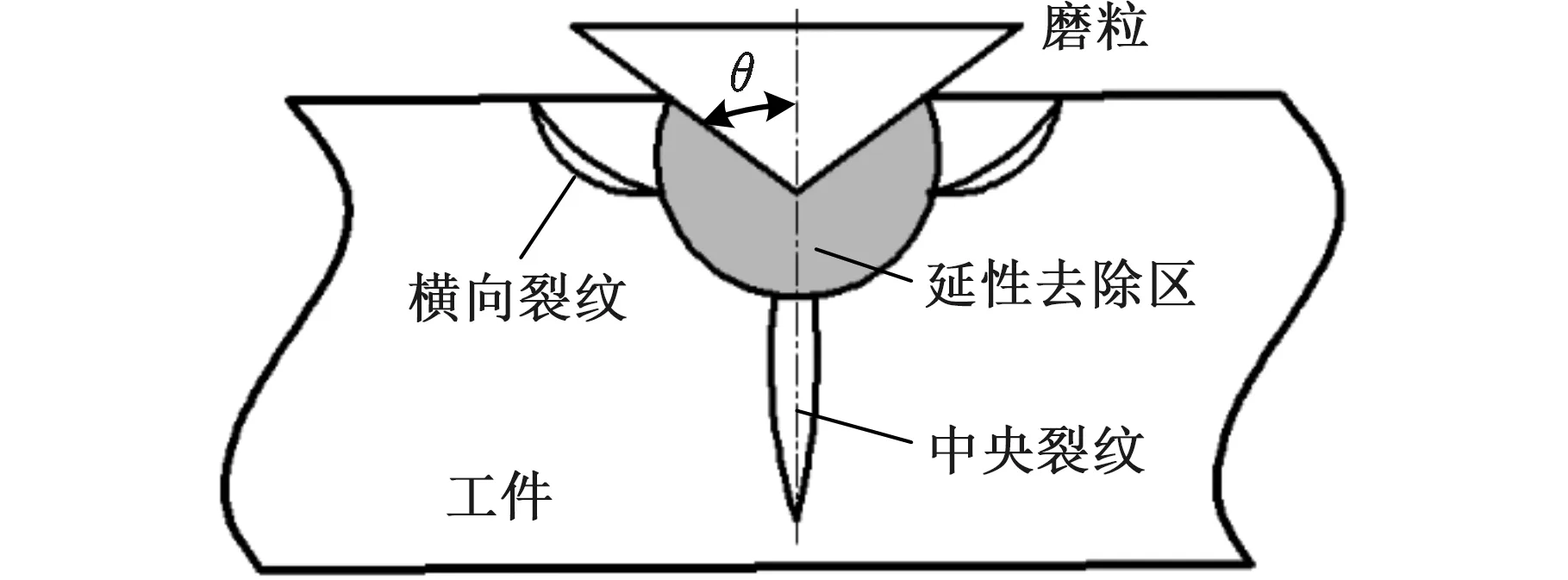
圖5 單顆磨粒壓痕模型[27]

WU等[28]考慮砂輪輪速和最大未變形切屑厚度hmax變化引起的應變率效應，建立了動態斷裂韌性模型：

(9)

式中，a、b為實驗確定的常數。

修正了臨界切削深度模型。

馬廉潔等[29]利用系數Kd表征加工參數帶來的動態效應，同時考慮微晶玻璃陶瓷磨削時的材料去除模式，得到了塑性-塑脆性臨界切削深度dc1和塑脆性-脆性臨界切削深度dc2：

(10)

式中，η1為塑性域系數；η2為塑脆性域系數；θ為磨粒錐頂半角。

材料塑性去除不但與臨界切深相關，還受成屑厚度的影響。磨削最大未變形切屑厚度hmax如圖6所示[28]。LIU等[30]進行了鈉鈣玻璃的納米級塑性域加工，結果表明：塑性切削主要由未變形切削厚度決定，當最大未變形切屑厚度hmax小于臨界值時，可以實現塑性域加工。

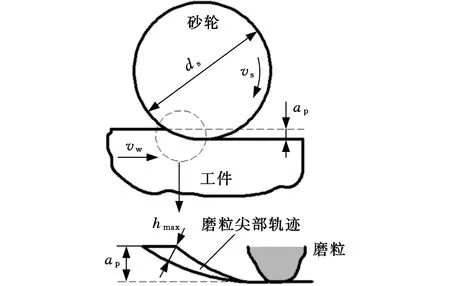
圖6 磨削最大未變形切屑厚度示意圖[28]

為方便分析，MALKIN等[31]將切削路徑近似成一段圓弧，如圖7所示，從而得到最大未變形切削厚度

圖7 平面磨削單顆磨粒磨削材料去除模型[31]

(11)

式中，s為轉過相鄰磨粒間隔時間內的工件平移量。

MALKIN等[31]假設磨粒尖端為球形，切削軌跡為圓弧，建立了切屑橫截面為矩形和三角形(圖8)的最大未變形切削厚度模型：

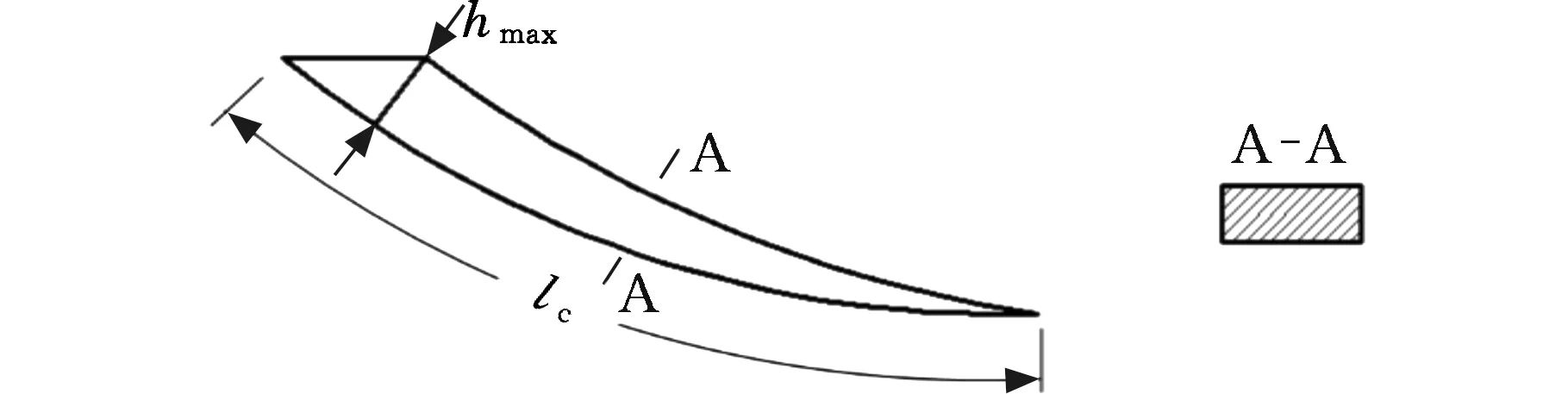
(a)矩形截面

(12)

式中，C為砂輪表面單位面積的有效磨粒數；r為切屑的寬厚比。

同樣地，MALKIN等[31]假設磨粒尖端為圓錐形，考慮磨粒頂角，建立了如下模型：

(13)

GOPAL等[32]考慮砂輪和工件局部接觸產生的彈性變形，對模型進行了修正：

(14)

式中，E1、E2分別為工件材料和砂輪的彈性模量；n為由實驗確定的常數。

JIANG等[33]基于磨粒粒徑正態分布、磨粒位置隨機分布的假設，考慮動態有效磨粒數，建立了最大未變形切削厚度模型：

(15)

式中，Nv為磨削時的動態有效磨粒數；xmax、dmax、g(x)、δ為表征磨粒粒徑的參數；Vcut為單個磨粒移動所去除的材料體積。

本文提到的主要臨界加工參數如表1所示。

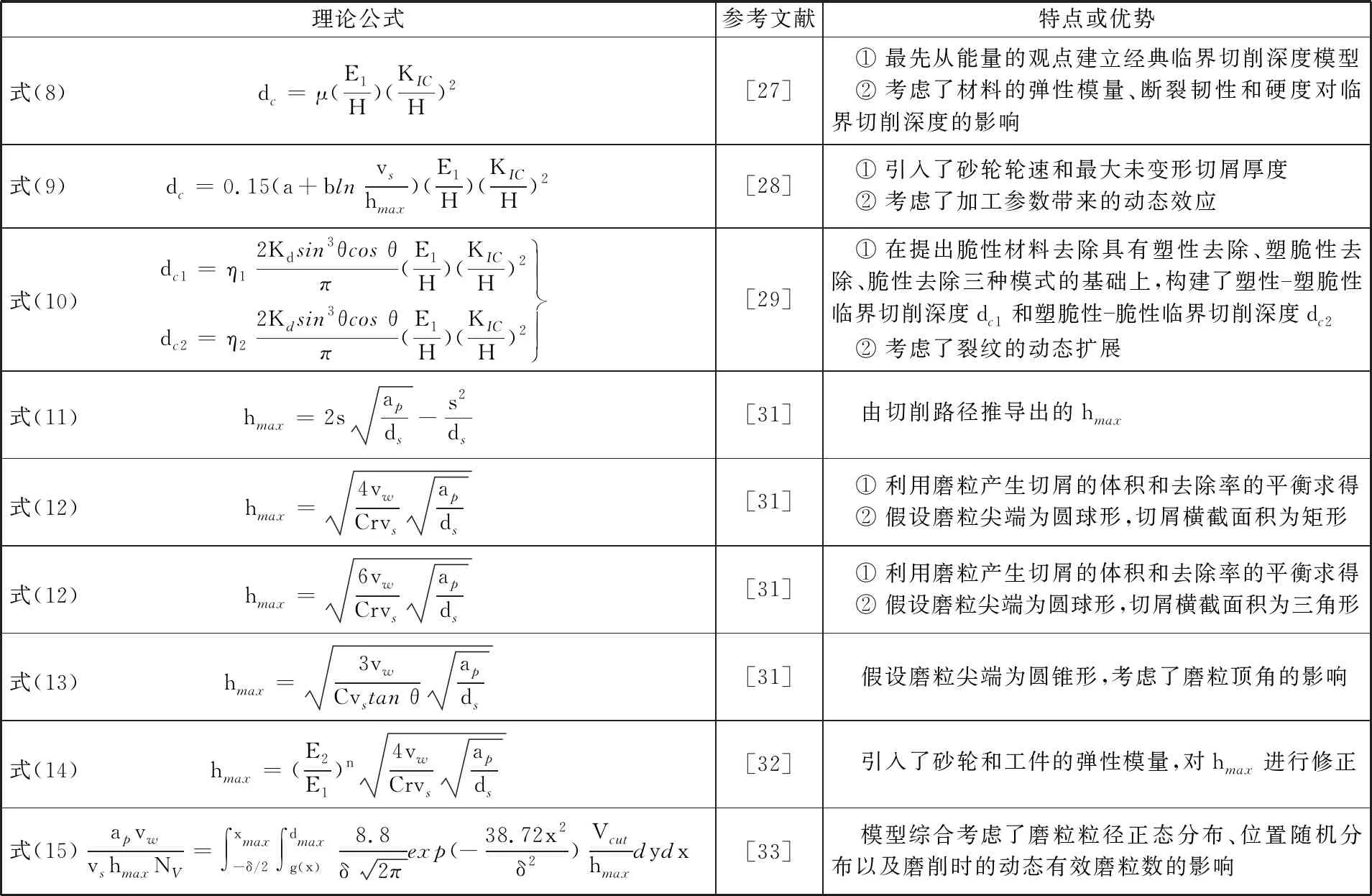
表1 主要臨界加工參數模型

3.2.2脆性材料去除模式

脆性材料的材料去除方式除了塑性去除和脆性去除外，還存在脆塑性共同去除[34-35]。脆性去除材料是通過裂紋的萌生、擴展直至切屑斷裂來實現的，表面會形成凹坑，影響表面質量，如圖9所示。塑性去除材料是在一定的加工條件下，切屑以剪切變形的形式被去除，得到無微裂紋的表面[36-37]。所以，不同的去除模式下，粗糙度存在著很大差異，在建立模型時，考慮材料的不同去除方式是很有必要的。

圖9 脆性材料切屑斷裂過程示意圖[1]

3.2.3表面粗糙度模型

AGARWAL等[38]結合陶瓷磨削實驗，做出如下假設：①磨粒尖端近似為圓形；②工件表面的凹槽輪廓相同，且完全由最大未變形切屑厚度定義；③不考慮凹槽重疊；④磨粒尖端和工件表面的干涉區域約為半圓。考慮磨粒出露高度和分布的隨機性，對表面凹槽進行簡化(圖10)，得到誤差較大的模型：

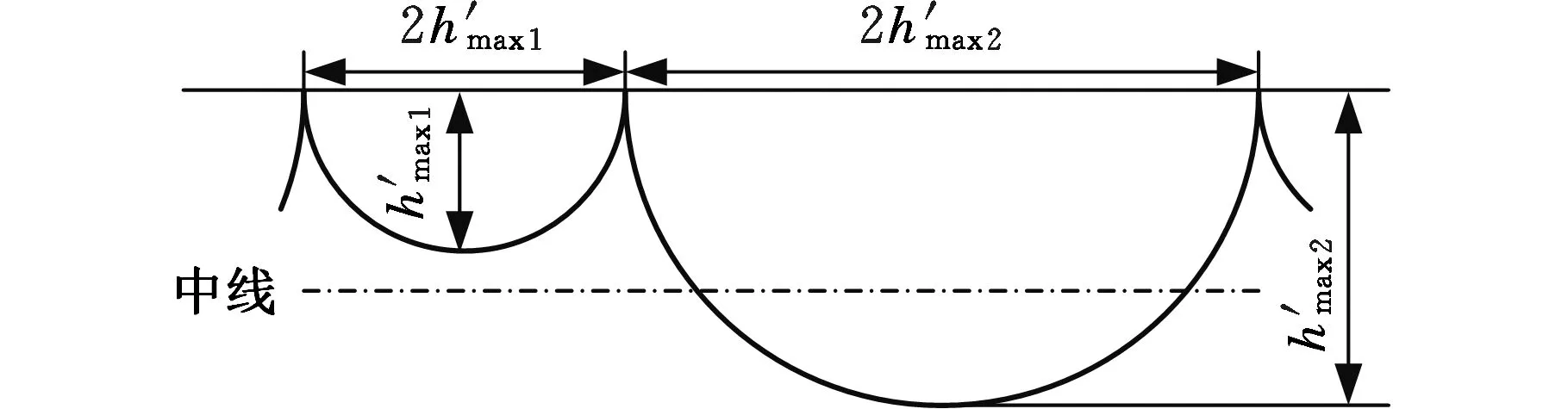
圖10 工件表面理想的凹槽輪廓[38]

E(Ra)=p1E(Ra1)+p2E(Ra2)=0.423E(h′max)

(16)

式中，E(Ra1)、E(Ra2)分別為凹槽深度小于和大于中線深度時的粗糙度期望值；p1、p2分別為凹槽深度小于和大于中線深度所對應的概率；h′max為三角形切屑橫截面的最大未變形切削厚度。

隨后，AGARWAL等[39-41]對模型進行修正，獲得了更為精確的粗糙度模型。

AGARWAL等建立模型時，雖然考慮了磨粒出露高度和分布的隨機性，但只考慮了材料塑性去除模式。實際加工過程中，隨著砂輪輪速降低或工件速度增加，材料去除機制將從塑性去除轉變為脆性去除，因此建立模型時也應考慮材料脆性去除產生的凹槽輪廓。

SHAO等[42]考慮到陶瓷磨削過程中的材料去除機制，假設：①磨粒尖端近似為圓錐形；②材料塑性去除產生的凹槽輪廓特征完全由最大未變形切屑厚度定義，材料脆性去除產生的凹槽輪廓取決于橫向裂紋系統，如圖11所示，將裂紋凹槽輪廓假設為三角形，如圖12所示；③不考慮凹槽重疊。基于以上假設得到粗糙度模型為

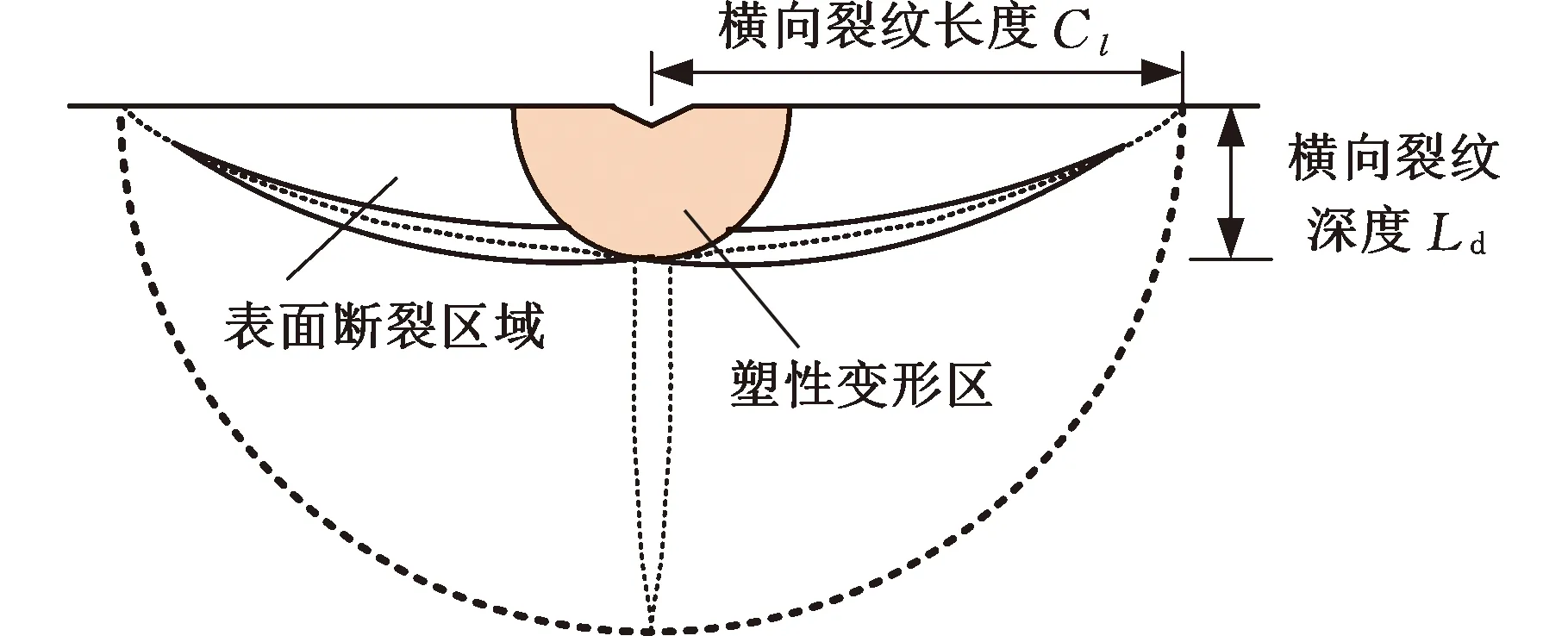
圖11 橫向裂紋系統示意圖[42]

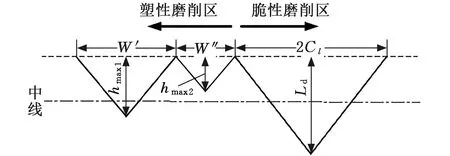
圖12 脆塑性結合去除模式下的表面粗糙度模型[42]

E(Ra)=P1E(Ra1)+P2E(Ra2)+P3E(Rabrittle)

(17)

式中，E(Rabrittle)為材料脆性去除對應粗糙度的期望值，P3為材料發生脆性去除所對應的概率；Rabrittle依據粗糙度定義進行求解[43-44]。

在平面磨床上進行碳化硅磨削實驗對模型進行驗證，驗證結果表明該粗糙度模型的平均誤差為5.65%。而AGARWAL等[41]的模型平均誤差為9.00%。

WU等[45]綜合考慮磨粒出露高度與分布的隨機性、磨削時的動態臨界切削深度、材料脆塑性共同去除模式，建立了一種新的粗糙度預測模型：

E(Ra)=P1E(Ra1)+P2E(Ra2)+PE(Rabrittle)

(18)

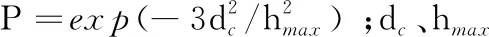
該模型更加符合實際情況，預測結果與實驗結果吻合良好(絕對誤差為3.27%)。

然而，SHAO等[42]、WU等[45]建立模型時均假設工件材料在塑性去除和脆性去除時都具有三角形橫截面，沒有對表面凹槽的形成機理進行深入分析，也未考慮凹槽重疊。

JIANG等[33]基于最大未變形切屑厚度模型(式(15))，模擬了磨削工件表面輪廓，SiC磨削實驗驗證該模型的計算結果與實驗數據吻合較好，磨削深度為35 μm時模型的最大誤差小于20%，磨削深度為5 μm時的誤差小于3%，該模型更適合用于高精度磨削加工。

MA等[20]根據脆性材料表面形成機理及大量實驗研究可知，最大未變形切屑厚度對加工表面的最終成形起主要影響，因此，基于Snoeys經驗模型和脆性材料表面形成機理提出了磨屑厚度粗糙度模型：

(19)

式中，hmax根據式(12)計算。

該模型考慮了切削路徑、加工參數和砂輪形貌等因素，進一步豐富了模型與材料去除機理的內在關系，經實驗驗證，該模型較Malkin模型和Snoeys模型的精度高。

點磨削表面粗糙度的解析式不包含砂輪偏轉角，所以通常認為點磨削表面粗糙度與偏轉角無關，但點磨削實驗結果表明：砂輪偏轉角對點磨削表面粗糙度的影響較大，其影響不容忽略。據此，MA等[2]深入探究了點磨削材料去除的內在機制和作用規律，首次提出了包含5個磨削因素(砂輪轉速、工作臺進給速度、磨削厚度、傾斜角和偏轉角)的點磨削表面粗糙度修正模型：

(20)

式中，hmax根據式(12)來計算；j、k為實驗確定的常數；α為傾斜角；β為偏轉角。

該模型推翻了點磨削表面粗糙度與偏轉角無關的觀點。

MA等[3]通過低膨脹微晶玻璃磨削實驗發現，表面粗糙度隨hmax的增大出現階躍性變化(圖13)，且存在著塑性去除和脆性斷裂共存的復合磨削階段，提出了復合磨削粗糙度模型：

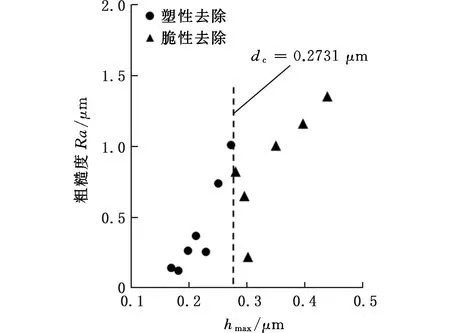
圖13 表面粗糙度隨最大未變形切屑厚度變化示意圖[3]

(21)

式中，dc、hmax分別根據式(9)和式(13)計算；ξ1、ξ2、λ1和λ2為與材料性能和加工條件有關的參數。

并進行了多因素交叉實驗進行驗證。復合磨削粗糙度模型較磨屑厚度粗糙度模型預測的精度高。

建立磨削表面粗糙度模型時，除考慮磨削參數和材料去除時的脆塑性轉變外，還需考慮磨粒磨損的影響。當前，考慮磨粒磨損的影響而建立的表面粗糙度模型一般都是針對金屬材料的，關于脆性材料的研究較少且不夠深入,因此，在今后的工作中，非常需要建立考慮磨粒磨損甚至動態磨粒磨損過程的脆性材料表面粗糙度模型。

MA等[1]考慮到陶瓷車削時的材料破碎機理，將含裂紋的切屑單元體類比為懸臂梁 (圖14)，基于裂紋擴展的最大拉應力準則和斷裂切屑單元的能量守恒原理，對凹坑的幾何特征進行量化(圖15)，建立了橫向表面粗糙度和縱向表面粗糙度理論模型：

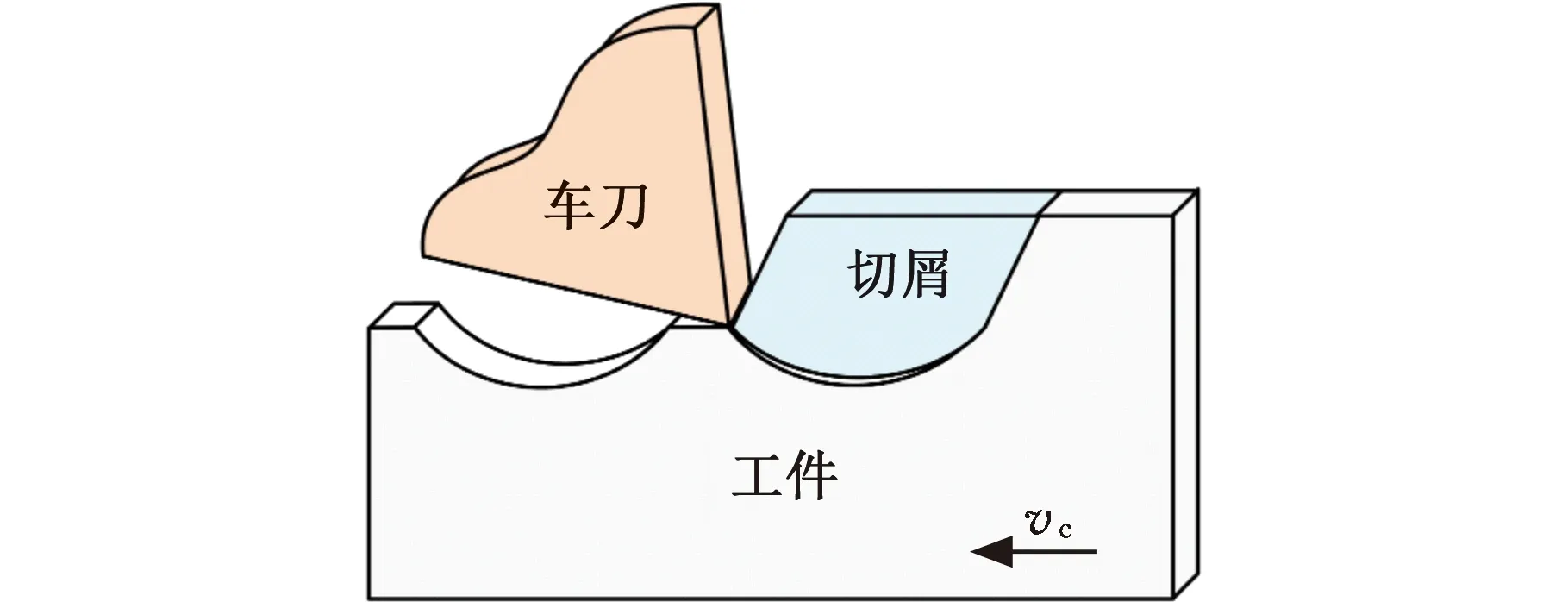
圖14 切屑形成過程示意圖[1]

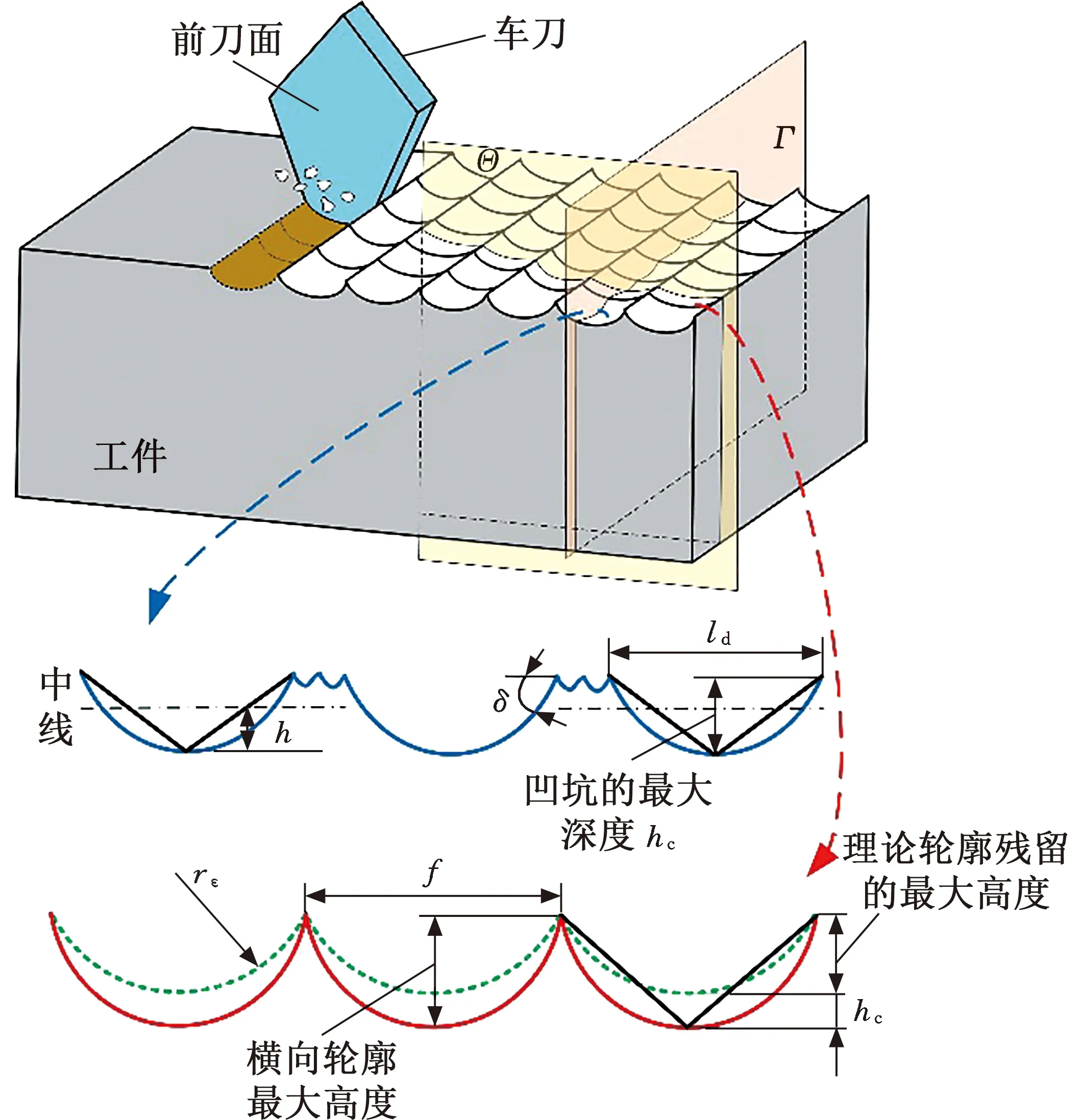
車削理想表面形貌 縱向表面輪廓 橫向表面輪廓

(22)

式中，Rat為橫向表面粗糙度；Ral為縱向表面粗糙度；lb為凹坑的長度；δ為凹坑的傾斜角。

該模型雖然考慮了脆性斷裂，但未考慮材料的塑性剪切，故僅適用于材料脆性去除模式。

隨后，馬廉潔等[46]綜合考慮材料脆性斷裂和塑性剪切共同去除模式，建立了粗糙度模型：

Ra=Rag+Rab

(23)

式中，Rag、Rab分別為幾何干涉粗糙度和脆性崩碎粗糙度；h為中線高度；χ0為與材料泊松比有關的本征屬性；Fp為切深抗力；Fc為主切削力。

該模型的預測值與實驗結果趨勢一致，但建模時未考慮刀具磨損對粗糙度的影響。

陳景強等[47]基于式(23)及車削脆性破碎機理和裂紋擴展準則，考慮刀具磨損，對模型進行了修正：

Ra=M(Rag+(Ra)′b)

(24)

式中，M為新形成的表面面積與理想表面面積的比值；(Ra)′b為修正脆性崩碎粗糙度；c為錐形裂紋長度；σ1為前刀面對工件的正應力；σ2為后刀面對工件的剪應力。

試驗驗證結果表明，脆性去除時，理論預測值與實驗值趨勢相同，模型精度明顯提高。刀具磨損是動態過程，且刀具磨損與刀具本身材料屬性、切削工件的材料屬性、切削參數等密切相關，對考慮磨損因素的理論模型需深入研究。

ZHANG等[48]綜合考慮運動學、塑性側流、材料彈性回彈和裂紋效應等因素，分別以切削刃輪廓的復制效應來計算運動學粗糙度分量Ride，以斜切削等效切削刃半徑的經驗表達式來估計材料彈性回彈粗糙度分量p，以未去除材料體積和塑料側流的比例系數來表征塑性側流粗糙度分量e，以裂紋長度模型來量化裂紋效應粗糙度分量Rc，建立粗糙度模型：

Ra=Ride+k0(p-e)+Rc

(25)

式中，k0為將峰-谷粗糙度轉換為算術平均粗糙度的恒定轉換系數。

相比于不考慮裂紋效應的粗糙度模型，該模型精確度更高。

本文提到的主要的粗糙度機理模型如表2所示。

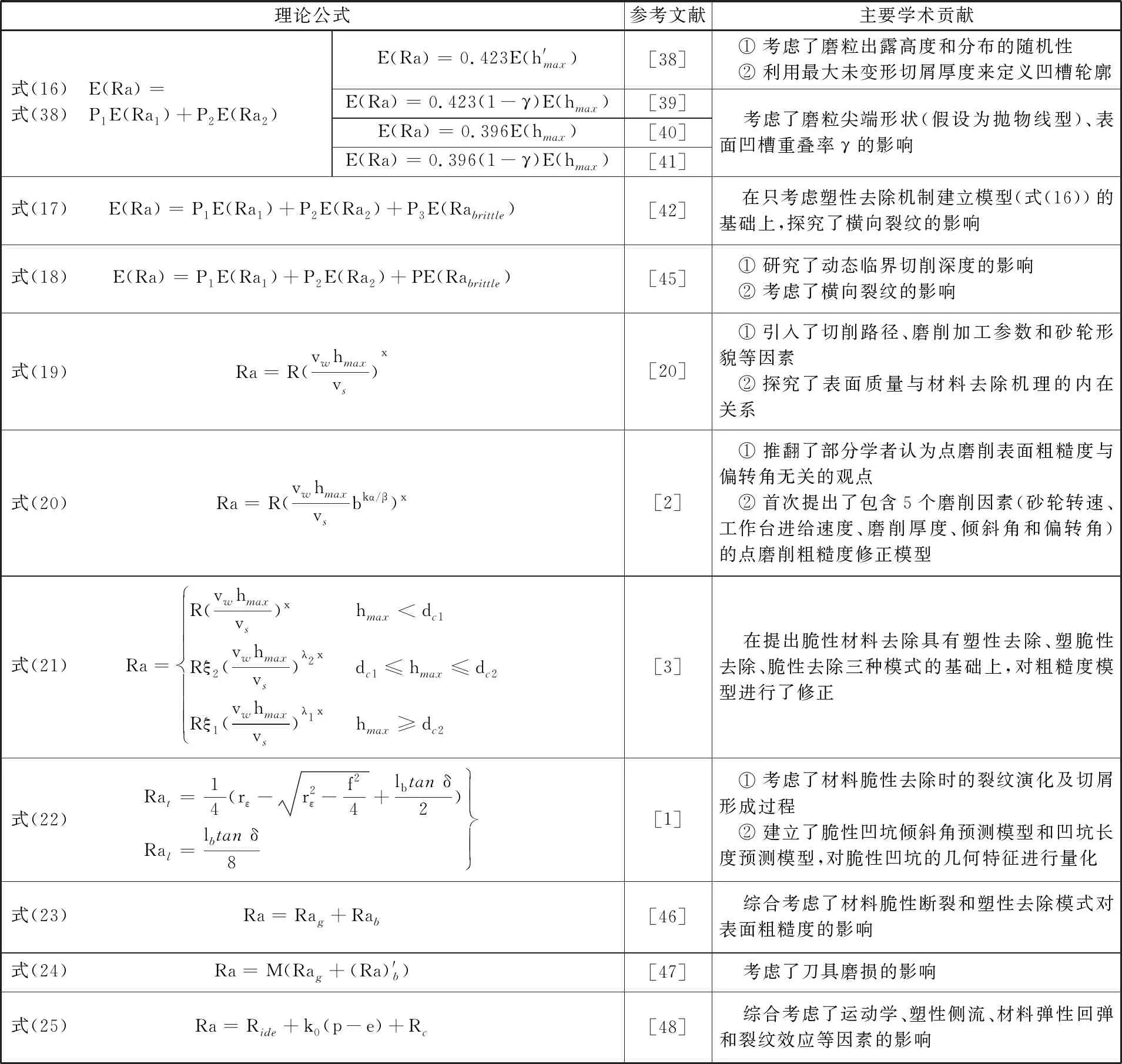
表2 主要的粗糙度機理模型

4 展望

(1)切削刃磨損隨切削過程的持續而不斷累積，對工件表面粗糙度的影響在脆性材料的加工中尤為突出，同時，切削要素、工件材料、冷卻條件等因素對刀具磨損均可產生不同程度的影響。所以，把切削刃磨損狀態引入表面粗糙度的研究之中，則表面形成機制更為復雜，但更符合加工實際。當前沒有針對脆性材料加工中刀具磨損對表面粗糙度影響進行深入研究，因此，開展考慮切削刃磨損的脆性材料表面粗糙度問題的研究非常必要。

(2)加工過程中，切削液、材料晶體取向等因素對表面粗糙度影響權重較大，但是這些因素難以定量表達，這些非量化因素對表面粗糙度影響的內在作用機理尚待研究。

(3)經驗參數建模方法與理論建模方法各有所長，理論模型是基于已有的基本原理或定律建立的，具有普遍適用性，經驗參數建模方法側重于數據挖掘，在解決非量化參數建模問題時，經驗參數方法優勢顯著。因此，結合兩種方法來研究表面粗糙度建模是未來的發展方向之一。