讓創(chuàng)新之花在數(shù)學(xué)課堂精彩綻放
——基于對習(xí)題探究課的賞析有感

?江蘇省如東縣洋口鎮(zhèn)初級中學(xué) 袁陳佳

隨著新課程理念的深化，教師越發(fā)關(guān)注對學(xué)生創(chuàng)新能力的培養(yǎng).當(dāng)然，培養(yǎng)學(xué)生創(chuàng)新能力的方法很多，對于數(shù)學(xué)教學(xué)而言，最簡單、最直接、最有效的方法莫過于提供豐富的學(xué)習(xí)素材，讓學(xué)生解決豐富多彩的、具有創(chuàng)造性的數(shù)學(xué)問題.問題作為課堂教學(xué)的主要方式，對教學(xué)效果的影響直接而深遠(yuǎn)，恰到好處的問題可以引發(fā)學(xué)生的創(chuàng)新靈感，培養(yǎng)學(xué)生的思維能力[1].下面，筆者從習(xí)題探究課的視角出發(fā)，具體闡述如何讓創(chuàng)新之花在數(shù)學(xué)課堂中精彩綻放.

1 以典型習(xí)題為載體，引發(fā)一題多解，收獲層出不窮的成功喜悅

一些簡單的常規(guī)題，學(xué)生在解決的過程中勢必“胸有成竹”，對學(xué)生自信心的建立效果顯著.而常規(guī)習(xí)題對培養(yǎng)學(xué)生的創(chuàng)新思維意義不大，相反會讓越來越多的學(xué)優(yōu)生喪失解題興趣，對數(shù)學(xué)學(xué)習(xí)十分不利.一些具有創(chuàng)新色彩的典型習(xí)題，其神秘不僅體現(xiàn)在思路的隱蔽上，還表現(xiàn)在奇妙的構(gòu)思上，更重要的是可以讓學(xué)生在一題多解的過程中培養(yǎng)學(xué)生思維的靈活性和創(chuàng)造性.因此，教師需要以典型習(xí)題為載體，給足學(xué)生審題和思考的時空，為學(xué)生提供一題多解的情境，使其大膽提出想法并進一步勇敢嘗試，從而在拾級而上的數(shù)學(xué)探索中收獲層出不窮的成功喜悅.

例1已知正方形ABCD中，點E落在邊BC上，且異于端點B,C，將EA繞著點E順時針旋轉(zhuǎn)90°至EF，連接CF.證明：CF為正方形ABCD的外角平分線.

師：請仔細(xì)審題，并說一說你準(zhǔn)備怎么去解這道題.(學(xué)生陷入思考)

生1：如圖1，過點F作FH⊥CG于點H，若能得出∠FCH=45°，即可證得CF為正方形ABCD的外角平分線.

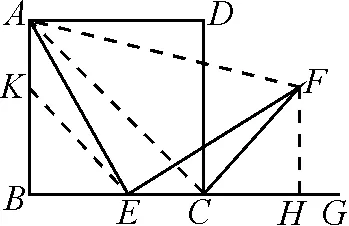
圖1

生2：由已知可得AE與EF相互垂直且相等，若是以AE，EF為邊借助旋轉(zhuǎn)構(gòu)造全等三角形即可解決本題.

生3：如圖1，連接AF，易得△AEF為等腰直角三角形，若能得出△FCH與△AEF間的關(guān)系即可解決本題.

生4：我覺得可以連接BD，并證明BD∥CF，就可以完成證明了.

生5：我認(rèn)為本題若是過點F作∠DCG兩邊的垂線段，并證明這兩條垂線段長度相等，那么問題就可以解決了.

師：你們都是有想法的好孩子！既然有了想法，何不來試一試呢？下面請大家選擇一種方法來解決本題.(學(xué)生在教師的引導(dǎo)下進行解題嘗試，由于時空充足，學(xué)生得出了以下多種多樣的精彩證法.)

證法1：利用AAS，容易證明△ABE≌△EHF，從而得出AB=EH.因為AB=BC，所以EH=BC，故BE=CH.由△ABE≌△EHF，可得BE=FH，所以CH=FH.由此可得△FCH為等腰直角三角形，所以CF為正方形ABCD的外角平分線.

證法2：因為∠BAE=∠CEF，∠BAE=∠CAF，所以∠CEF=∠CAF，據(jù)此可得A,E,C,F四點共圓.因為∠AEF為直角，所以∠ACF為直角，從而∠DCF=90°-∠ACD=45°.故CF為正方形ABCD的外角平分線.

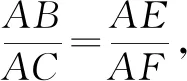
證法4：在邊AB上取一點K，使AK=CE，不難證明△AKE≌△ECF.因為KB=BE，所以△KBE是一個等腰直角三角形，于是∠BKE=45°，則有∠AKE=∠ECF=135°，從而∠FCG=45°.故CF為正方形ABCD的外角平分線.

學(xué)生都是獨具個性的個體，看待相同的問題由于角度不同，想法也會各不相同.對于例1，學(xué)生給出的各種證法中，不管是構(gòu)造全等，還是尋求相似，又或是利用平行，都是從自身的解題經(jīng)驗中提取出來的.有想法就會有創(chuàng)新，教師基于學(xué)生的數(shù)學(xué)思考巧妙地進行“留白”，留給學(xué)生足夠的思考與探索的時空，讓學(xué)生表露自己的初步想法，引發(fā)更加深刻的思考，促進問題的正確解決.這里例1發(fā)揮了其典型效能，讓學(xué)生在一題多解的過程中復(fù)習(xí)了三角形全等、相似以及圓等相關(guān)知識，在各種知識的融合貫通中學(xué)會了解決錯綜復(fù)雜的綜合問題，很好地促進了創(chuàng)新思維的發(fā)展.

2 以錯誤為契機，因勢利導(dǎo)，歷練自由創(chuàng)新的思維

新課程理念為數(shù)學(xué)教學(xué)帶來了勃勃生機，想要讓學(xué)生能駕馭創(chuàng)新思維之舟，需要教師的適當(dāng)引導(dǎo)和點撥[2].在數(shù)學(xué)課堂中，“犯錯”并非偶然，可以說具有一定的必然性，錯誤是美麗的，是動態(tài)生成的.因此，我們要允許學(xué)生犯錯，將學(xué)生的錯誤視為一種資源和契機因勢利導(dǎo)，促進學(xué)生歷練自由創(chuàng)新的思維.

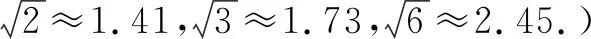
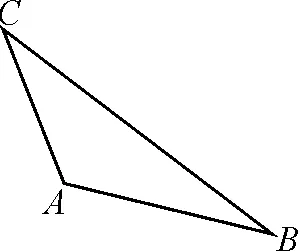
圖2

師：請在思考后說一說你打算嘗試的解題思路.(學(xué)生思考，并很快有了想法.)

生1：如圖3，可以過點A沿著水平與豎直方向各作出兩條線，與BC分別交于點M和N.

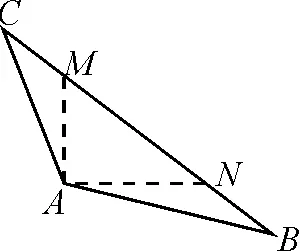
圖3

生2：如圖4，可以過點A作AC的垂線，與BC相交于點H.

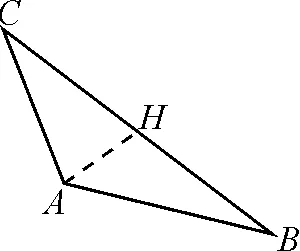
圖4

生3：如圖5，過點C作AB的垂線，與AB的延長線相交于點K.

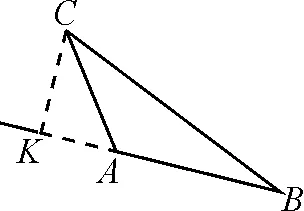
圖5

師：那么在添加輔助線之后，圖中多出了哪些三角形，這些三角形對于解題有何作用？

生1：作出圖3后，原三角形被切割為等腰三角形ACM，含有30°角的Rt△MAN及△ANB.但△ANB中有已知邊長無特殊的角，Rt△MAN與等腰三角形ACM有特殊角卻無已知邊長，那么似乎這樣作輔助線并不好用.

師：你們在解題中也有類似的困惑嗎？

生2：我也有.作出圖4，Rt△CAH含有30°角，但也一樣沒有已知邊長.

生3：我也同樣有困惑.作出圖5，△CAK為等腰直角三角形，也同樣沒有已知邊長，所以題中的已知條件一樣無法靈活運用.

師：失敗乃成功之母.通過剛才的嘗試我們知道在三角形中求邊長通常可將普通三角形轉(zhuǎn)化為特殊三角形，再借助三角函數(shù)建立邊與角之間的關(guān)系來探求邊長.那么可以再深入思考一下，如何能利用轉(zhuǎn)化思想得出我們需要的三角形呢？

生4：如圖6，過點B作CA的垂線與其延長線交于點Q，構(gòu)成的△AQB不僅為特殊三角形，也有一條邊可知.

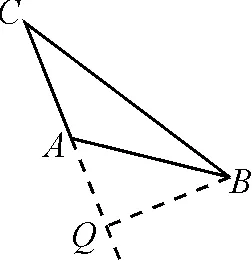
圖6

師：從失敗中吸取教訓(xùn)，進行深刻反思，在反思后進一步嘗試，終于得出了符合要求的三角形，也探尋到了解題的入口，非常好！從前面幾名學(xué)生添加輔助線失敗的經(jīng)歷我們可以看出，正是因為都存在缺陷才導(dǎo)致了失敗，那么現(xiàn)在再細(xì)致地思考一下，這些缺陷能否彌補呢？(學(xué)生又一次陷入深思，細(xì)細(xì)思量問題.)

生5：從生2所作的圖4出發(fā)，如圖7，進一步再過點B作AH的垂線，與AH的延長線交于點Q.因為△AQB是等腰直角三角形，AB=12，所以可得又Rt△BHQ中，∠HBQ=30°，則故從而

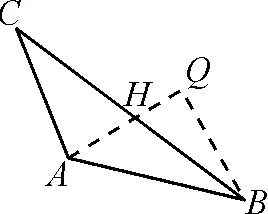
圖7

師：非常好!事實上，若是從圖3出發(fā)，如圖8，進一步過點B作AN的垂線，交AN的延長線于點P，再借助勾股定理也可以讓本題獲解.只是在整個解析的過程中運算繁瑣，一般我們不會選擇這種解法，有興趣的學(xué)生也可以在課余時間進行嘗試……

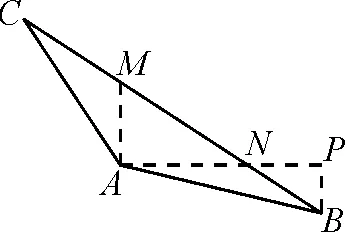
圖8

直覺與經(jīng)驗是學(xué)生創(chuàng)新思維的基石，在拋出例題后，教師引導(dǎo)學(xué)生憑借自身的已有經(jīng)驗和直覺水平進行嘗試.學(xué)生在一番思索之后，生成了各種各樣的想法，并循著想法進行嘗試，由于作出的三角形無益于問題的解決從而從內(nèi)心深處很快被否決掉.而此時，教師并沒有一口否決學(xué)生的想法，而是循著其原生思維的脈絡(luò)，鼓勵其深度思考，從錯誤中探尋機遇，讓錯誤綻放異樣的光彩，這樣一來，極好地訓(xùn)練了學(xué)生的創(chuàng)新思維，提高了學(xué)生的解題能力[3].

總之，問題的設(shè)計取決于教學(xué)目標(biāo)，教師的引導(dǎo)關(guān)乎學(xué)生思維抵達的深度與廣度，影響教學(xué)效果.因此，教師需精心設(shè)計問題并付諸課堂實踐，以典型例題引發(fā)一題多解，以錯誤為契機因勢利導(dǎo)，培養(yǎng)學(xué)生創(chuàng)新思維，讓創(chuàng)新智慧之花在課堂綻放.我們有理由相信，以問題為載體，以追問為引導(dǎo)，必將讓學(xué)生的創(chuàng)新思維邁上一個新臺階.