誤差傳遞公式的教學(xué)探索

蔡 丹 楊 濤 陳國華

（桂林電子科技大學(xué)材料科學(xué)與工程學(xué)院 廣西·桂林 541004）

0 前言

在大學(xué)物理實驗中，最終的測量目標(biāo)都是間接測量量。間接測量的結(jié)果是由直接測量結(jié)果按照一定的表達(dá)式計算出來的。因此，直接測量結(jié)果的誤差（或不確定度）就必然影響到間接測量結(jié)果，這種影響的大小也可以通過相應(yīng)的表達(dá)式計算出來，即誤差傳遞公式（注：誤差傳遞公式（error propagation formula）是2019年經(jīng)全國科學(xué)技術(shù)名詞審定委員會審定發(fā)布的物理學(xué)名詞）。

誤差傳遞公式是誤差分析的基礎(chǔ)，同時也是教學(xué)過程中的重點和難點。理工類專業(yè)的學(xué)生，學(xué)習(xí)大學(xué)物理實驗課程的目標(biāo)不應(yīng)局限于僅僅掌握相關(guān)的實驗操作技能以及正確的測量數(shù)據(jù)方法，還應(yīng)該能夠正確的進(jìn)行數(shù)據(jù)處理和誤差分析，給出合理的實驗結(jié)果，明確主要誤差的來源。從而在后續(xù)的設(shè)計性實驗中進(jìn)行誤差分配，正確選擇儀器。

1 學(xué)情分析

大部分國內(nèi)高校開設(shè)的大學(xué)物理實驗課程在第一次授課時，都會專門安排一節(jié)緒論課，對物理實驗中的基本操作常識、儀器用法和誤差理論進(jìn)行講解。由于誤差傳遞公式是誤差分析必不可少的工具，也被放到了緒論課中。但在后續(xù)進(jìn)入具體實驗項目之后，教師們一般都不會再花時間對相應(yīng)實驗中所用的誤差計算公式進(jìn)行推導(dǎo)或解釋。因此，如何在上緒論課時就將這個貫穿始終的知識點講解明白，就顯得十分的重要。

然而筆者在多年教學(xué)過程中感受到，很多學(xué)生并沒有很好的理解和掌握誤差傳遞公式，即便記住了公式卻也“知其然，不知其所以然”。相應(yīng)的，在學(xué)生所上交的實驗總結(jié)報告中，誤差分析部分通常總是完成得最不理想的部分。可見，如何改進(jìn)教學(xué)方法，使學(xué)生學(xué)得好，教師容易教，便是迫切需要解決的問題。

本校選修大學(xué)物理實驗課程的通常都是大一下學(xué)期及大二上學(xué)期的理工科專業(yè)學(xué)生，筆者通過調(diào)查發(fā)現(xiàn)，在講解緒論課時大多數(shù)專業(yè)的學(xué)生正在或者剛剛學(xué)完高等數(shù)學(xué)課程中關(guān)于多變量微積分的章節(jié)。俗話說：“數(shù)理不分家”，于是筆者嘗試在講解誤差傳遞公式時，將數(shù)學(xué)知識與物理實驗更緊密的聯(lián)系起來，讓學(xué)生從多個角度去認(rèn)識和理解誤差傳遞公式，從而更好的掌握這個重要的知識點。

2 教學(xué)設(shè)計

物理學(xué)中物理規(guī)律一般都可用數(shù)學(xué)形式表示，即所謂“公式”，但它又與純數(shù)學(xué)公式有所不同。數(shù)學(xué)公式不一定有物理意義，而有物理意義的定律、定理，就一定能寫出數(shù)學(xué)公式。物理規(guī)律是自然界萬事萬物遵守的規(guī)律，這個規(guī)律用公式寫出來，就成為定量科學(xué)。規(guī)律寫不出，或無法寫出一個具體的數(shù)學(xué)公式，只能語言講解時，就是定性科學(xué)。現(xiàn)在的物理學(xué)中，仍然有很多定性而沒有達(dá)到定量的程度。

常用的系統(tǒng)誤差傳遞公式及適用條件實驗中總是伴隨著誤差的存在。由于某些儀器的零點不準(zhǔn)、不等臂，理論公式的近似，某些實驗條件的不滿足和各種儀表的接入誤差等原因，都可能產(chǎn)生系統(tǒng)誤差。在計算時，一般采用系統(tǒng)誤差的傳遞公式，我們不著急按照教材推導(dǎo)誤差傳遞公式，而是首先通過一個簡單的例子來說明，直接測量的誤差（或不確定度）是為何，以及如何傳遞到間接測量的結(jié)果上。

在高等數(shù)學(xué)中，微分代表的是變量的變化量。而在物理實驗中，某個變量在一定的范圍之內(nèi)變化又可以理解為其真實值存在著一定的不確定度，或者說誤差。因此，我們將上式中的微分號d替換為代表不確定度的，即

如此，我們就建立了一種把直接測量的不確定度與間接測量的不確定度相關(guān)聯(lián)的表達(dá)式，也即誤差傳遞公式。但是，若用上式進(jìn)行不確定度的計算，可能會因為右端各項之間正負(fù)抵消，導(dǎo)致對測量結(jié)果不確定度的估計過于樂觀。因此，很多教材中將誤差傳遞公式定義為：

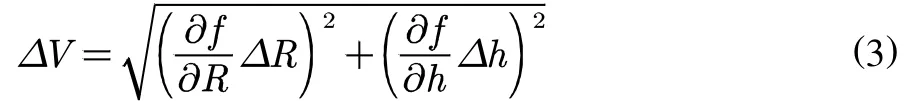
可見，R和h的不確定度都會對V的測量結(jié)果產(chǎn)生影響，而兩者的影響力取決于各自偏導(dǎo)數(shù)的大小。

以上推導(dǎo)過程與間接測量的計算表達(dá)式無關(guān)，可以概況為三步，即：第一步，計算全微分；第二步，微分換成不確定度；第三步，改寫為“方和根”。利用同樣的思路，也可以得到計算相對不確定度的表達(dá)式。

[例2]已知x、y和z為直接測量量，W為間接測量量，且滿足。

首先對函數(shù)f兩邊取自然對數(shù)，即：

把微分號d替換為不確定號，即：

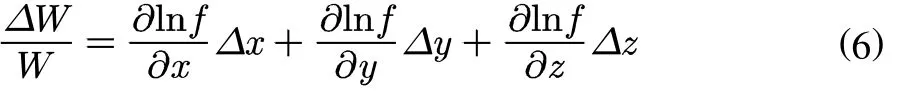
最后改寫為“方和根”，即

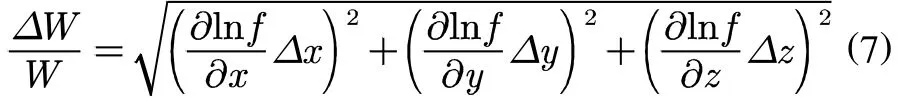
3 結(jié)語

數(shù)理結(jié)合的教學(xué)設(shè)計，在一定程度上降低了學(xué)生對于誤差傳遞公式的理解難度。問卷調(diào)查顯示，超過80%的學(xué)生表示理解并容易接受上述“三步走”的推導(dǎo)過程。對比分析后發(fā)現(xiàn)，采用新教法授課的學(xué)生，其實驗總結(jié)報告中誤差分析部分的正確率有了明顯的提高。當(dāng)然，學(xué)生的學(xué)情、課程設(shè)置、課程要求等都是動態(tài)變化的，需要在教學(xué)過程中不斷地進(jìn)行探索和創(chuàng)新。