平面向量問題中的求解策略

■楊 立 劉大鳴(特級教師)

高考對平面向量仍將以向量的線性運算,向量的夾角以及最值問題進行重點考查,凸顯數形結合思想、轉化與化歸思想的具體應用。

策略1：利用平面向量基本定理化歸幾何問題

圖1

評注：用平面向量基本定理解題的一般思路:先選擇一組基底,并將條件和結論中的向量用該基底表示,再通過基底向量的運算來解決。

策略2：利用模的平方將向量問題實數化

評注：|a|2=a2=a·a可以實現由數的運算到向量的運算的轉化,因此遇到向量的模就要有先平方的意識。

策略3：利用數量積運算求向量的夾角

評注：解答本題的關鍵是要熟記兩個向量夾角的取值范圍是[0,π]。

策略4：利用數量積的最值合理轉化為函數的最值

例4 如圖2,半圓的直徑AB=6,O為圓心,C為半圓上不同于A,B的任一

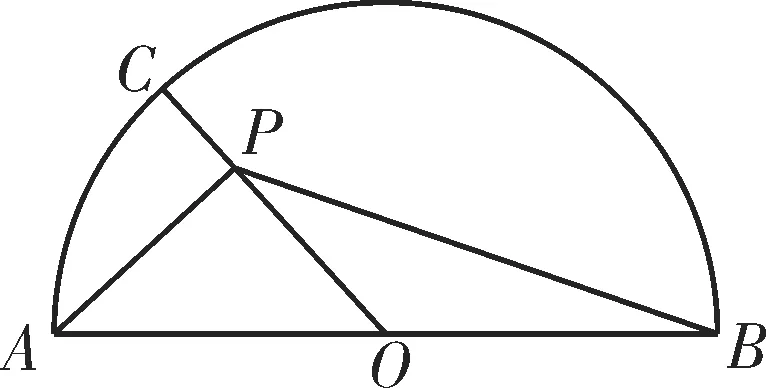
圖2

評注：由于數量積為實數,因此可以將數量積的最值轉化為函數的最值求解。