考慮初始缺陷的附著式升降腳手架穩定性分析

李鵬舉，劉光明，徐 彬，王 琪，周 磊

(1.中鐵城建集團第一工程有限公司，山西 太原 030024；2.山東大學，山東 濟南 250100； 3.杭州市錢江新城投資集團有限公司，浙江 杭州 310000)

1 概述

強度問題、剛度問題和穩定性問題都是鋼結構受力性能分析中很重要的部分[1]。本文主要分析鋼結構的穩定性問題。在以往的研究中，何法偉等[2]以鋼構件的振動頻率值作為監控參數，分析了鋼構件在失穩過程中軸向荷載同一階振動頻率的關系；劉霞等[3]基于ABAQUS有限元軟件分析鋼框架在失穩時內部能量的變化，從能量方面對鋼框架倒塌進行了預測和分析；趙羿[4]針對于單層網殼鋼結構冷卻塔節點研發、節點抗彎性能及結構靜力穩定性能開展研究，給出了考慮偏心受力作用的節點剛度半剛性鋼冷塔穩定性分析的迭代方法。

上述研究對于鋼構件失穩進行大量研究，但目前國內外學者對于考慮初始缺陷的附著式升降腳手架穩定性分析研究投入較少。由于附著式升降腳手架存在工作面離地面遠且桿件多的特點，若在使用附著式升降腳手架時發生結構整體或局部失穩的情況，則會造成嚴重的工程事故。因此本文考慮初始幾何缺陷、材料非線性的非線性穩定性分析，對附著式升降腳手架進行屈曲穩定分析，相關研究成果可為提高附著式升降腳手架的安全穩定性提供參考。

2 工程概況

本文基于濟南市某超高層項目，本項目主要由1棟34層主塔樓及其6層裙房和2層整體地下車庫組成，主塔樓建筑高度為165.5 m，結構類型為框架-核心筒，樓層邊柱均為傾斜型鋼混凝土柱，每根柱切斜角度不同。本工程34層主塔施工至第7層后考慮搭設附著式腳手架，直至主塔主體結構封頂后，完成爬架高空拆除。

3 特征值屈曲有限元分析

3.1 材料參數

所取附著式腳手架每榀外排高度20 m，內排高度18 m，架體寬度0.6 m，水平跨度為10 m。使用有限元軟件ANSYS進行建模分析，模型整體采用Beam188單元進行模擬，采用理想剛接模擬螺栓連接[5]，架體構件材料均為Q235鋼材，容許應力為205 MPa，材料參數見表1，架體材料截面尺寸見表2，有限元模型見圖1。

表1 模型材料參數

表2 附著式升降腳手架構件尺寸表

3.2 計算工況和荷載選取

根據《建筑結構荷載規范》，不同工況下活載取值如表3所示。

表3 施工活荷載標準值

本工程只有在主體結構施工過程中去使用腳手架。另外，由于頂上兩層腳手板是人員施工主要活動的地點且施工器械材料也大量堆積在此，因此選取頂上兩層腳手架進行活載施加。按照以下兩種荷載效應組合進行分析：1)恒載+施工活載；2)永久荷載+0.9(施工荷載值+風荷載)。

3.3 分析結果表

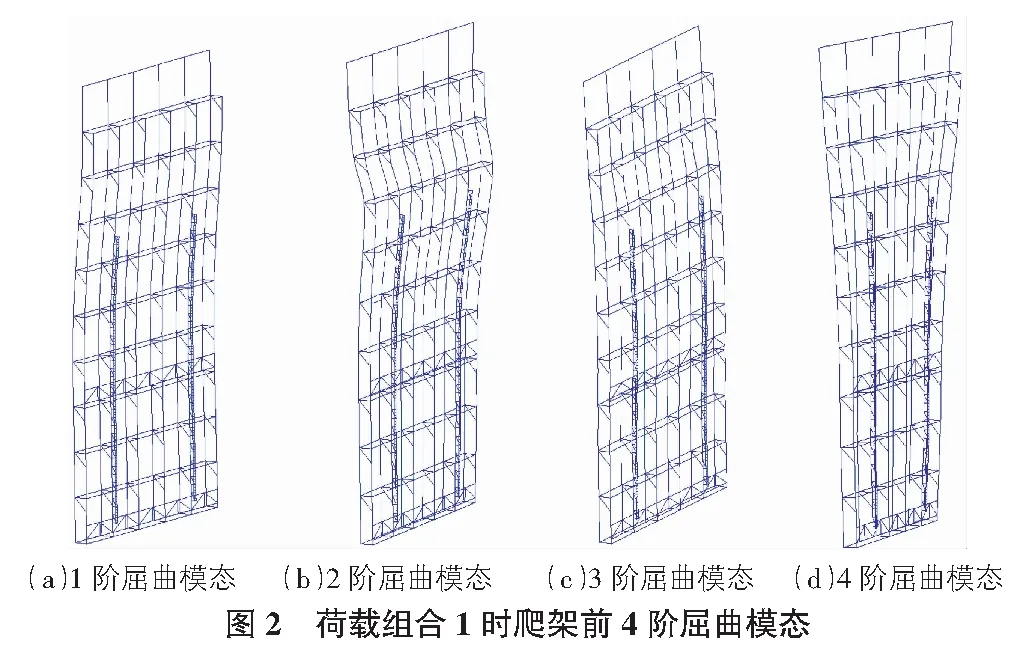
雖第1階失穩模態為最容易發生失穩的形式，但因其對應的屈曲荷載較大，實際情況中產生第1階失穩模態的可能性較低，因此本文特征值屈曲分析中，主要考慮4階屈曲模態和屈曲系數。

1)荷載組合1：恒載+活載(見表4，圖2)。

表4 荷載組合1時附著式腳手架屈曲分析結果

2)荷載組合2：恒載+0.9(活載+風載)(如表5，圖3所示)。

表5 荷載組合2時附著式腳手架屈曲分析結果

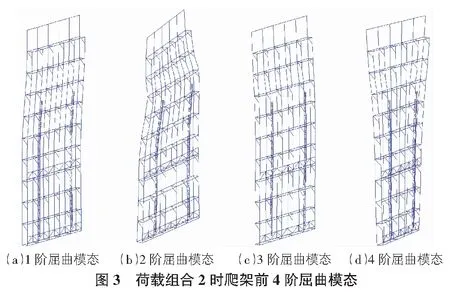
從表4和表5中看出，荷載組合1中1階屈曲安全系數是15.774；荷載組合2中1階屈曲安全系數是16.586，數值均大于1。這說明爬架提升時抗失穩性能較好，抗失穩性能滿足實際工程中屈曲系數大于3的實際需求[6]。

由圖2，圖3對比觀察到，爬架的前4階屈曲模態基本一致。在荷載組合2效應作用下的前4階的屈曲安全系數比在荷載組合1作用下的值都要大。兩個荷載組合的差別主要在于荷載組合1沒有考慮風荷載，而荷載組合2考慮到了風荷載，這說明在不考慮風荷載的作用下爬架屈曲更容易發生。爬架提升作業在風速大于5級時禁止進行可能為產生上述現象的原因，因此本文在分析屈曲模態時考慮較小的風荷載。

4 非線性穩定性有限元分析

在實際安裝和使用過程中，爬架結構的初始缺陷是無法避免的，爬架結構材料的非線性行為也是客觀存在的[7-9]。本節在特征值屈曲分析研究的基礎上，考慮初始缺陷和材料非線性行為，對爬架進行非線性穩定性有限元分析[10]，提高爬架穩定性的計算精確性。采用弧長法[11]對結構幾何非線性問題進行跟蹤求解，并采用BKIN模型描述爬架的非線性行為。表6為根據相關文獻[12-13]及現場查看總結的附著式腳手架初始缺陷統計表。

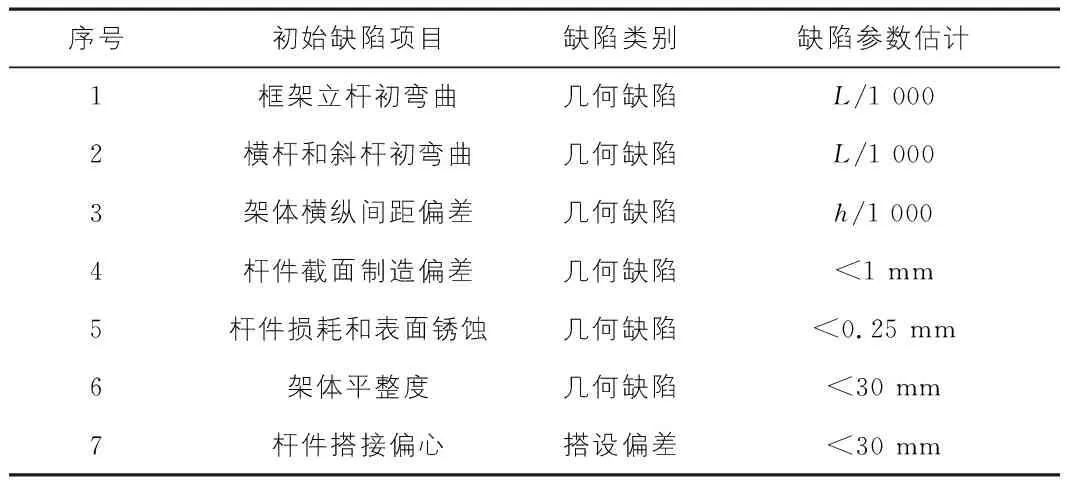
表6 附著式升降腳手架初始缺陷統計

4.1 模型加載

在ANSYS特征值屈曲分析中求得的屈曲系數是全荷載作用的縮放系數，由此得出式(1)。

結構屈曲荷載=屈曲系數×(恒載+活載)

(1)

由于式(1)不符合工程的實際情況，因此編寫迭代計算APDL語言(見圖4)，對所選荷載工況進行迭代求解至1階屈曲系數輸出結果為1，由此得出式(2)。

屈曲荷載=1.0×(恒載+活載系數×活載)

(2)

由式(1)與式(2)的對比觀察到，式(2)符合工程實際。在荷載組合1作用下輸出的1階特征值屈曲活載屈曲系數為38.24，之后再乘以1.2的載荷系數。得到的值作為非線性穩定分析的初始活載并將其施加于架體，加載過程采用弧長法。

4.2 分析結果

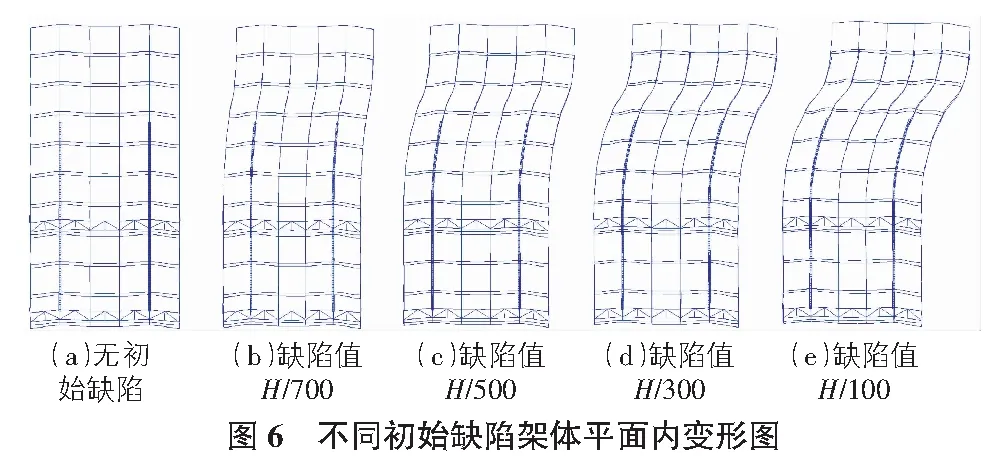
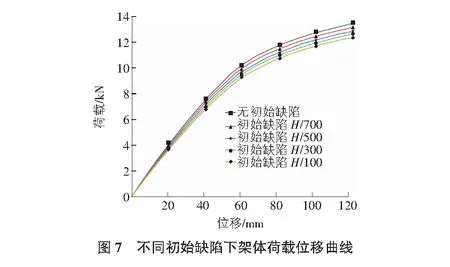
考慮初始幾何缺陷的爬架變形有限元計算結果如圖5，圖6所示，不同初始幾何缺陷數值下節點荷載位移曲線如圖7所示，相應的極限承載能力和穩定系數見表7，表8。

根據以上分析結果可得出以下結論：

1)由表7可以看出，隨著初始幾何缺陷的增大，架體的極限承載能力逐漸降低，由13.1 kN下降至12 kN，僅僅下降了8.4%。這說明初始幾何缺陷的變化對附著式升降腳手架極限承載能力的影響小。

2)由圖5，圖6可以看出，從無初始缺陷到缺陷值逐漸增大的過程中，架體平面內剛度和平面內扭轉剛度不斷降低，架體變形幅度不斷增長，且變化幅度均十分明顯。架體的失穩模態包括平面外彎曲失穩、平面內彎曲失穩和沿中線扭轉失穩三種。這說明在考慮初始幾何缺陷后架體的失穩模態變化較大。

3)由表8可以看出，從無初始缺陷到缺陷值逐漸增大的過程中，特征值屈曲分析整體穩定系數基本不發生變化，基本一直保持在38.24左右；從無初始缺陷到缺陷值逐漸增大的過程中，非線性穩定性分析整體穩定系數從14.56下降至13.33。這說明特征值屈曲分析整體穩定性系數偏不保守且基本不隨缺陷值的改變發生變化。

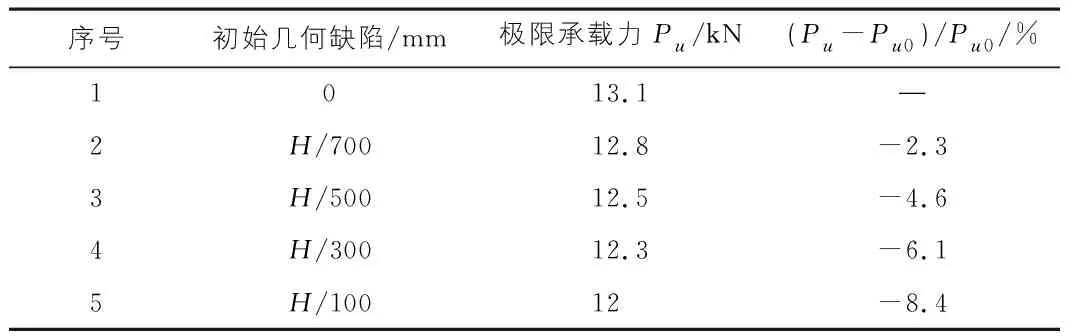
表7 非線性分析極限荷載統計表

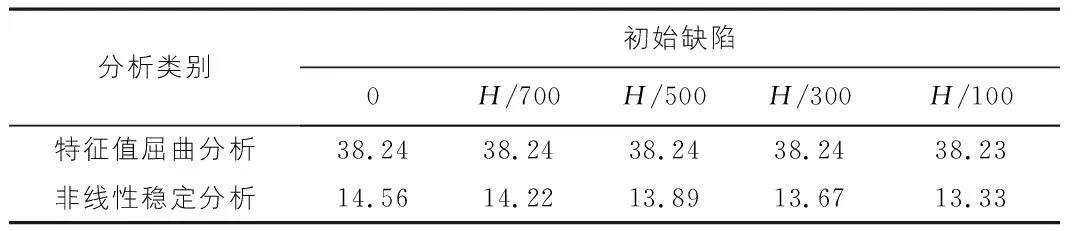
表8 爬架整體穩定系數統計表

5 結語

本文通過建模分析可以看到，特征值屈曲分析整體穩定性系數偏不保守且基本不隨缺陷值的改變發生變化，不可以用于實際工程；在結構非線性行為中，從無初始缺陷到缺陷值逐漸增大的過程中，整體穩定系數下降明顯，爬架失穩模態更復雜，且較特征值屈曲分析下的整體穩定系數下降程度大，實際工程用此方法進行爬架穩定分析更為準確合理。