Phase-field modeling of faceted growth in solidification of alloys

Hui Xing(邢輝) Qi An(安琪) Xianglei Dong(董祥雷) and Yongsheng Han(韓永生)

1The Key Laboratory of Space Applied Physics and Chemistry,Northwestern Polytechnical University,Xi’an 710029,China

2College of Materials Science and Engineering,Zhengzhou University,Zhengzhou 450001,China

3The EMMS Group,State Key Laboratory of Multiphase Complex Systems,Institute of Process Engineering,Chinese Academy of Sciences,Beijing 100190,China

Keywords: faceted growth,dendrite,phase-field model

1. Introduction

Faceted growth of semiconductors such as Si, Ge and SiGe mixtures in undercooled or supersaturated melts has been attracted great interest in crystal growth field because their huge applications for electronics and photovoltaics industries.[1]It is well known that Jackson’s factorα,[2]the product of the crystallographic factor and the ratio of latent heat to the rare gas constant, approximately describes the tendency of a material to facet. This has been proved in a wide range of materials.[3]Previous experimental investigations from semiconductor to intermetallic demonstrate that the faceted crystal at equilibrium could become less faceted and a transition from facet to dendrite occurs with the undercooling or supersaturation increasing.[4-6]This results from that the faceted crystal still retains tailing rough parts which can be described by a parabolic function at equilibrium. Therefore,the key point of numerical simulation of the faceted growth and its transition to dendrite is how to construct a form of anisotropic function exhibiting perfectly flat vicinal interface with rounded cusps at equilibrium. Obviously, the general form of surface tension anisotropic function cannot be used.The form of anisotropic function for facet in the presence of cusps at faceted orientations can be written as

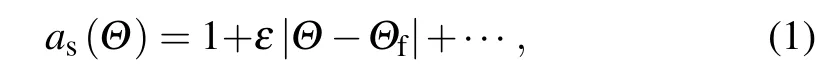
whereΘis the angle of the normal direction to the interface with respect to a fixed crystalline axis,andΘfis the orientation of a facet. Equation(1)is indeed valid for a vicinal interface when|Θ-Θf|?1,andεis the cusp amplitude. As a powerful tool for simulating growth pattern selection,the phase-field method has been quantitatively and extensively used for simulating growth pattern selection in the non-faceted dendritic growth with weak and strong anisotropy from undercooled or supersaturated melts.[7-9,11]For faceted growth,it is impossible to separately treat the rough and faceted parts in the framework of the phase-field method. Hence, many attempts have been made for constructing a continuous form of surface tension anisotropic function for faceted growth.[12-17]By modifying a simple form of anisotropic function

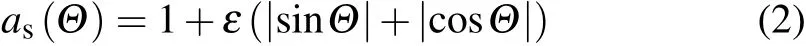
from broken-bond model for faceted solid-gas interface, numerical simulation of the faceted dendritic growth with cusp rounding have been successfully carried out by using phasefield method by Debierreet al.[12]However,the modification of the anisotropy function consists of rounding the cusp over a small range of orientations

Obviously, Eq. (4) is similar to the form given by Eq. (2) in principle, but it is a handy form to solve numerically. There is no physical meanings of the parameterδ, which is a small but not negligible constant in numerical simulation. The addition ofδto Eq. (4) allows a continuous interface stiffness.Similar form for six-fold anisotropic function was constructed by Bolladaet al.[16]to investigate the intermetallic solidification of Al-Si alloys and the transition from faceted to dendritic morphology. In this paper, the form of Eq.(3)is adopted for studying faceted growth in solidification of a binary alloy from supersaturated melts in a two-dimensional system.

2. Method descriptions

We consider the growth of a crystal from a supersaturated alloy melt. The quantitative phase-field model for alloys solidification is developed based on the thin-interface asymptotic analysis by Karma.[18]This model can be successfully used for simulating non-faceted dendritic growth in solidification of alloys due to the inclusion of the anti-trapping current term. The phase-field variableφis-1 (+1) for solid (liquid) and the narrow region where it varies from-1 to +1 is considered as the diffusive solid-liquid interface.For alloys solidification, the solute concentrationcwas converted to the solute supersaturationU, which is defined asU=((2kc/c0)/[1+k-(1-k)φ]-1)/(1-k), wherec0the concentration on the liquid side of the interface andkthe partition coefficient. After neglecting the solute diffusion in the solid phase,governing equations for phase-field variableφand solute concentrationUyield

is the well-known anti-trapping current term,matched asymptotic analysis links diffusive interface widthW0and interface attachment time scaleτ0with capillary lengthd0and liquid diffusion coefficientDlbyW0=λd0/a1andτ0=λa2W20/Dlfor vanishing interface kinetic coefficient,wherea1=0.8839 anda2=0.6267. In this work, the modified surface tension anisotropic function Eq. (4) for faceted growth by Wanget al.[15]was used here. In this study, the well-characterized Si-3.5 at.% Ge alloy in solidification[19]was selected as the calculation object,and all thermophysical parameters were assumed constants which are listed as follows: average solute concentrationc0=3.5 at.%, equilibrium liquidus slopeml=-1.85 K/at%,equilibrium partition coefficientk=0.45,liquid diffusion coefficientDl=6200 μm2/s, and Gibbs-Thomson coefficientΓ=0.2324 K·μm. The coupling constantλis selected asλ=2 for results that are independent of the interface thickness. In numerical simulation,governing Eqs.(5)and(6)are solved by using the explicit finite difference method on a fixed grid. No-flux boundary conditions are applied to all boundaries. The numerical domain is set as 800×800. As shown in Fig.1,the initial solid seed is introduced as a quarter of square or circle for the reason of symmetry to investigate the effect shape of initial seed of growth pattern selection.

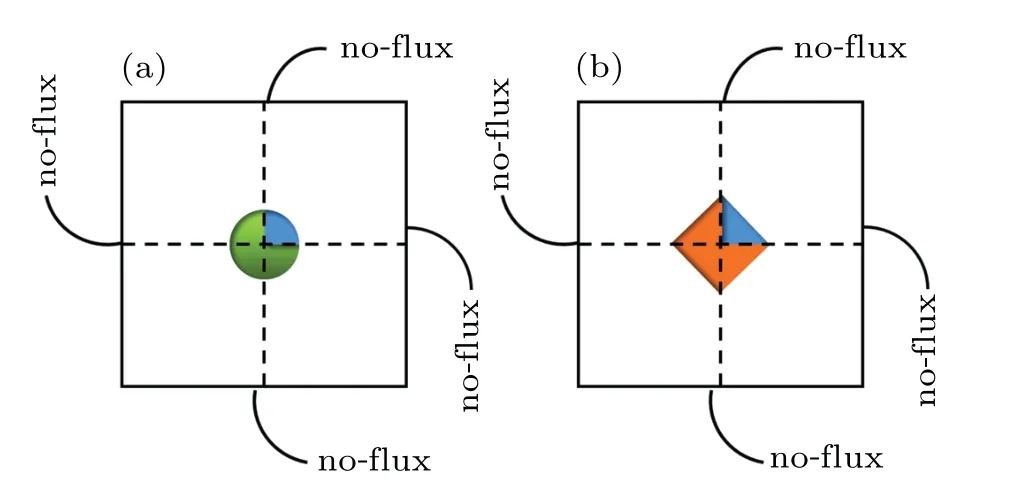
Fig. 1. Schematic of boundary conditions and initial solid seeds: (a)circl and(b)square.

3. Results and discussion

The value ofδis firstly chosen from 0.1 to 0.005 in two cases of supersaturation for a proper value ofδin numerical simulation. Solutions of Eq. (3) forδvarying from 0.1 to 0.005 are shown in Fig. 2(a). The solution of Eq. (2) has a sharp cusp atΘ=0 while solutions of Eq. (3) with finite values ofδare smooth at a small range nearΘ=0. It can be seen that the profiles from Eq.(3)become convergent with the decrease inδ, which indicates that the effect ofδis only remarkably in the region nearΘ=0 similar to the solution of Eq.(2)but Eq.(3)is a continuous function.In order to demonstrate the effect ofδon the crystal growth, we carried out two-dimensional phase-field simulations for variousδin two cases of supersaturationU0=0.20 andU0=0.50,which corresponds to square and dendritic shapes,respectively. Shapes with solute distributions are shown in Figs. 2(b)-2(g). Obviously,phase-field simulations with Eq.(3)exhibit perfectly flat vicinal interface with rounded cusps for lower supersaturation,as shown in Fig.2(b). Due to the growth velocity proportional to the absolute value of the supersaturation,the diffusion length forU0=0.20 is significantly larger than that forU0=0.50.In order to investigate the role ofδ,the solid-liquid interface contours for variousδwith an enlarged drawing near the tips are plotted at the same time. For lower supersaturation, as shown Figs. 2(c) and 2(d), the interface profiles for variousδoverlap except the region near the tip. Clearly, the convergence with respect toδhas been achieved with the decrease ofδnear the tip. For larger supersaturation, as shown in Figs. 2(f) and 2(g), the shape becomes dendritic and the difference of the interface profile for variousδbecomes pronounced. Therefore,a smallerδshould be selected for larger supersaturation. The above study proves that Eq.(3)is a simple but good regularization for Eq.(2)for the cases of solidification. In the following numerical simulation,δ=0.001 are used everywhere.

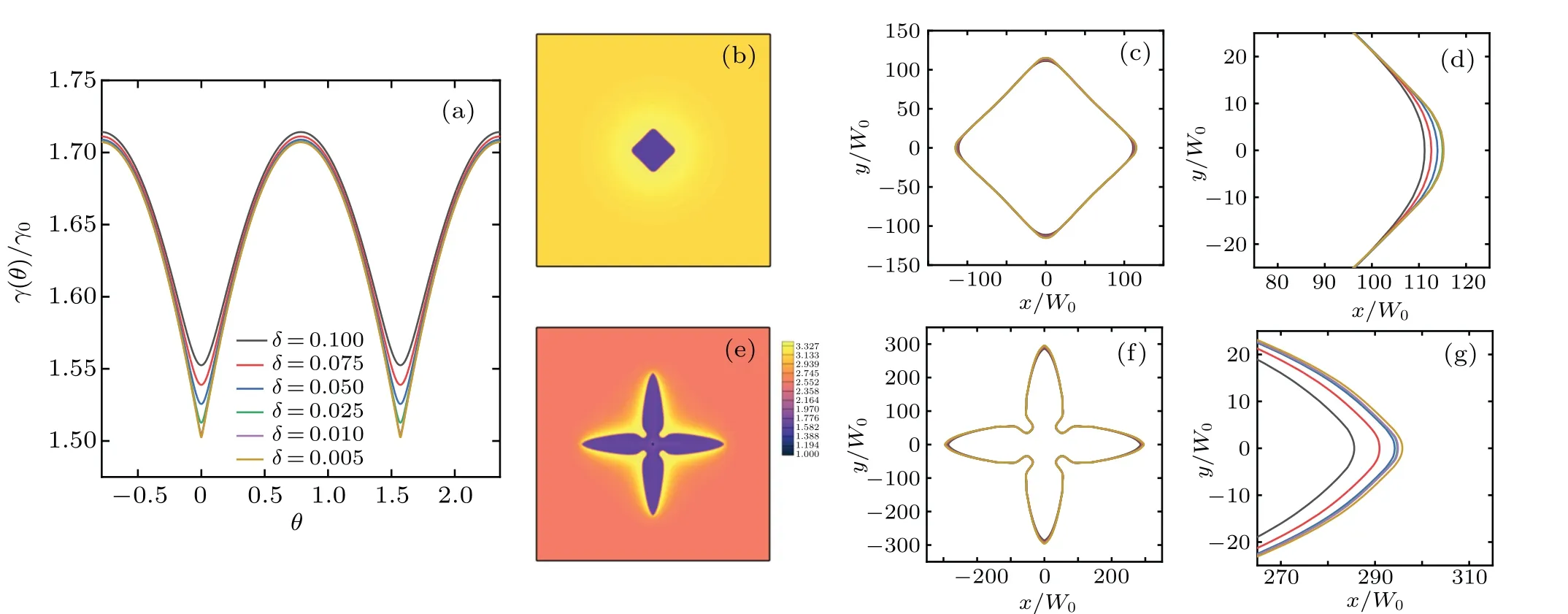
Fig. 2. (a) Solutions of the a regularization of the surface tension anisotropic function for δ varying from 0.1 to 0.005; solute distribution in square growth (b) and interface contours for various δ (c) with an enlarged drawing near the tips (d) for U0 =0.20; solute distribution in dendritic growth(e)and interface contours for various δ (f)with an enlarged drawing near the tips(g)U0=0.50.

For faceted growth, the initial shape of the solid seed plays an important role in growth pattern selection. Two values of supersaturationU0=0.425 andU0=0.475 are chosen and the cusp amplitude is fixed atε=0.5, as shown in Fig.3. It can be found that the solid-liquid interface contours from the two initial conditions overlap except the region of dendritic root forU0=0.425. For a little higher supersaturationU0=0.475, the square shape of the initial seed leads to a dendrite with a single tip while the circle shape results in complicated doublons shape with tip-splitting. Although the effect of initial seeds on the growth pattern selection is a numerical artifact,it is important for simulations of facet growth.This is consistent with the results from Ref.[12]. It should be noted that the doublons are symmetry-broken growth pattern with double tips that are highly dependent on the choice of the initial seed shape. The growth velocities of the leading tips with respect to the time for various initial conditions and supersaturations are presented in Fig.3(c). Clearly,the dendrite has a higher growth velocity than doublon when the growth becomes steady. This means that the initial seed should be square to simulate faceted growth in large supersaturation or undercooling.

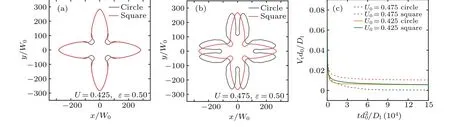
Fig.3. Comparision of interface contours from circle and square seeds for U0 =0.425(a)and U0 =0.475(b); (c)temporal evolution of the leading tip velocity for various initial conditions and supersaturations.

Fig.4. (a)Steady growth velocity versus the cusp amplitude ε with typical growth patterns;(b)steady growth velocity versus supersaturation with typical growth patterns.

Now, let us focus on the effect of the cusp amplitude and supersaturation on the growth pattern selection and steady growth velocity in faceted solidification. Figure 4(a) shows the steady growth velocity versus the cusp amplitudeεwith typical growth patterns forU0=0.50. In this study, the initial shape of the solid seed is square. It can be seen that the steady growth velocity increases with the cusp amplitude forε ≤0.8.Meanwhile the growth pattern becomes from doublon to dendrite. Lower cusp amplitude means the unstable tip,and increase of the cusp amplitude results in the steady growth direction. Whenε ＞0.8, the steady growth velocity decreases with the increase of the cusp amplitude, which is consistent with the finding in Ref.[16]. As expected,the steady growth velocity is an increasing function of supersaturation when the cusp amplitude is fixed atε=0.5,which is shown in Fig.4(b).Obviously,the morphological transition from cube to dendrite is continuous,which indicates that the transition can be quantitatively obtained from phase-field simulations by using the regularization of the anisotropic function Eq.(4).

4. Conclusion and perspectives

In this paper, the faceted growth has been numerically investigated by using a quantitative phase-field model with a regularization of the surface tension anisotropic function. The form of the anisotropic function has been used in predicting the vapor-liquid-solid nanowire growth. Results show that the value ofδcan only affect the region near the tip,and the convergence with respect toδcan be achieved with the decrease inδnear the tip. And the difference of the interface profile for large supersaturation is more pronounced than that for lower supersaturation. Moreover, the initial shape of the solid seed also plays an important role in growth pattern selection for faceted growth, and the circle initial seed results in the doublon when the supersaturation is larger. The steady growth velocity is not a monotonic function of the cusp amplitude,which is consistent with the finding in Ref. [12]. The maximum value is approximately atε=0.8 when the supersaturation is fixed. Moreover, the growth velocity is a monotonic function of supersaturation, or at least in the range of the supersaturation. This study is the basis of numerical simulations of faceted growth in solidification of alloys,which proves that the form of Eq. (4) is a simply but good regularization for faceted growth in solidification of alloys. Moreover, it also can be used in the thin film growth and spiral growth in the processing of CVD.

Acknowledgements

Project supported by the National Key Research and Development Program of China(Grant No.2018YFB2001800),the National Natural Science Foundation of China (Grant No. 21978298), the Natural Science Foundation of Shaanxi Province in China (Grant No. 2020JM-111), Applied Basic Research Key Project of Yunnan, China (Grant No.202002AB080001-1),and Henan Youth Talent Promotion Project,China(Grant No.2020HYTP019).